三坐标测量机测头系统的误差分析与修正

杜翠翠，徐强，冯旭刚，章家岩

(安徽工业大学电气与信息工程学院，安徽马鞍山243032)



三坐标测量机测头系统的误差分析与修正

杜翠翠，徐强，冯旭刚，章家岩

(安徽工业大学电气与信息工程学院，安徽马鞍山243032)

摘要：测头是三坐标测量机的关键部分，其动态性能对测量机最终测量结果有直接的影响。为了提高三坐标测量机测头的测量精度，以触发式测头系统为主，研究了测头系统动态误差的构成，分析了测头预行程误差来源及影响因素，提出了将测头直径动态标定与微平面补偿法相结合的方法对测头直径进行补偿。通过对凹轮轮廓进行测量，并在逆向工程软件中对测头直径补偿前后进行对比。结果表明，该方法对测量机测头直径有较好的补偿效果，具有一定的应用价值。

关键词：三坐标测量机；测头系统；预行程误差；测头直径

0引言

三坐标测量机的测头一直都是学者们的研究热点。文献[1]通过三维理论模型对测头的预行程进行了研究，文献[2]探索了坐标测量机测头的动态性能，文献[3]通过将刚体模型与测头中的误差函数相结合，从而建立了误差补偿模型。目前，国内外主要是通过对曲线或曲面拟合来对测头直径进行补偿，这种方法需要采集大量的轨迹数据,再利用最小二乘法进行曲线或曲面拟合[4-6]，计算较为繁琐。

因此，本文对测量机触发式测头误差进行了分析与修正，探究了预行程误差的影响因素，并采用测头直径动态标定与微平面补偿法相结合对测头进行直径补偿。只有高精度的测头才可以充分发挥坐标测量机的作用[7-8]，因此深入探究测头的动态误差并建模修正，可以提高三坐标测量机的整体测量精度。

1触发式测头的工作原理

如图1所示，3对接触副以120°均匀分布在圆柱体上，传动带动测头移动对被测工件进行测量。弹簧向下压紧，3对接触副会自动接触。当测头开始接触被测工件时，二者之间产生接触力且逐渐渐增大，直到达到预先设定的阈值，从而产生触发信号。机床收到触发信号之后，控制系统发出暂停动作指令，从而停止测头的移动。触发信号被用来控制测量机光栅系统记录当前坐标值[9-10]，并通过通信模块将坐标值进行计算机间的数据传递，完成测量任务[11]。

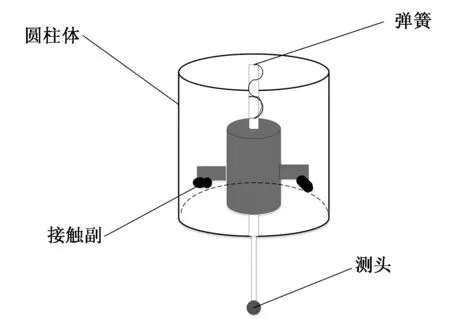
图1　测头结构简图

测头测量时的位移误差[12]为

δx(x)=δx(x)1+δx(x)2=

εy(x)c+εy(x)l+εy(x)p]hr

式中：δx(x)为测头的位移误差；εz(x)a为测头绕z轴在a点的俯仰角误差；εy(x)p，εy(x)b，εy(x)l,εy(x)c分别为y滑架绕y轴横梁在点p,b,l,c处的俯仰角误差;K(d,l)为测力函数；hr为主轴伸出长度;hc为右支柱的高度。

该测头结构虽然结构简单，抗干扰能力强[13],但对被测工件的同一点进行测量时，需要触发力不尽相同，从而导致重复性误差加大，带来预行程误差等。

2测头预行程误差分析

由测头结构及工作原理可知，测头测端与被测工件接触至产生触发信号之间的距离称之为预行程[14]。预行程对测头测量精度的影响很大，而影响测头预行程的因素有很多，像测力大小方向、测头直径、测杆刚性及测量速度与逼近距离等。

测头的预行程公式[15-16]如下：

W=Wh(φ,θ)+We(φ,θ)+Ws(φ,θ)

Δd=Δβ·lp式中：Wh为测量机测杆的弹性变形；Ws测杆位移；We为测头与接触工件之间的Hertz变形；Δd为瞄准误差；φ,θ分别为测头在球坐标下的方位角和极角；Δβ为测杆的偏转角；lp为测杆的等效长度。

3测头直径补偿研究

简单曲面测量如图2所示。

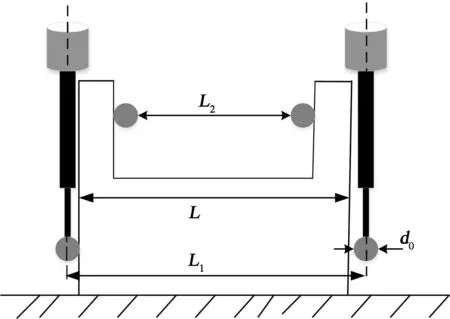
图2　简单曲面测量示意图

当测头对简单曲面进行测量时，则实际被测工件尺寸为：

外尺寸=L1-d0

内尺寸=L2+d0

式中d0为测头直径。

复杂曲面测量如图3所示。

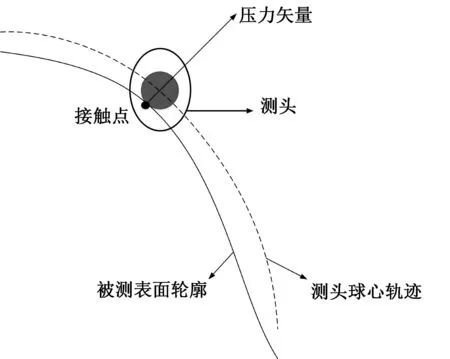
图3　复杂曲面测量示意图

当测头对不规则曲面进行测量时，被测工件的尺寸不再是增减测球直径d0，而是求取被测工件接触点的法矢。

基于此，经过大量实验模拟，提出将测头直径动态标定与微平面补偿法相结合的方法对测头进行直径补偿。下面对此方法进行详细介绍。

1)测头直径动态标定。在测头对被测工件进行实际测量时，不仅要对测头进行静态校准，而且还需要对测头进行标定，从而获得较高精度的测量结果。其中，对测头标定还需设定有关参数，如DCC参数[17](临近距离a、移动速度v1、探测速度v2)等等。

为了探究DCC参数对测头直径标定的影响，减小测头动态误差，本文通过研究不同的DCC参数来计算测头直径d的变化情况。本实验以改进型MC850三坐标测量机为研究基础，其最大测量速度为vmax=500 mm/s,速度数值按照最大速度值的百分制计算。

该实验分为3组,①第1组，临近距离a和移动速度v1一定时，考察探测速度v2对测头直径d的影响；②第2组,临近距离a和探测速度v2一定时，考察移动速度v1对测头直径d的影响；③第3组,移动速度v1和探测速度v2一定时，考察临近距离a对测头直径d的影响。实验结果如图4～6所示。

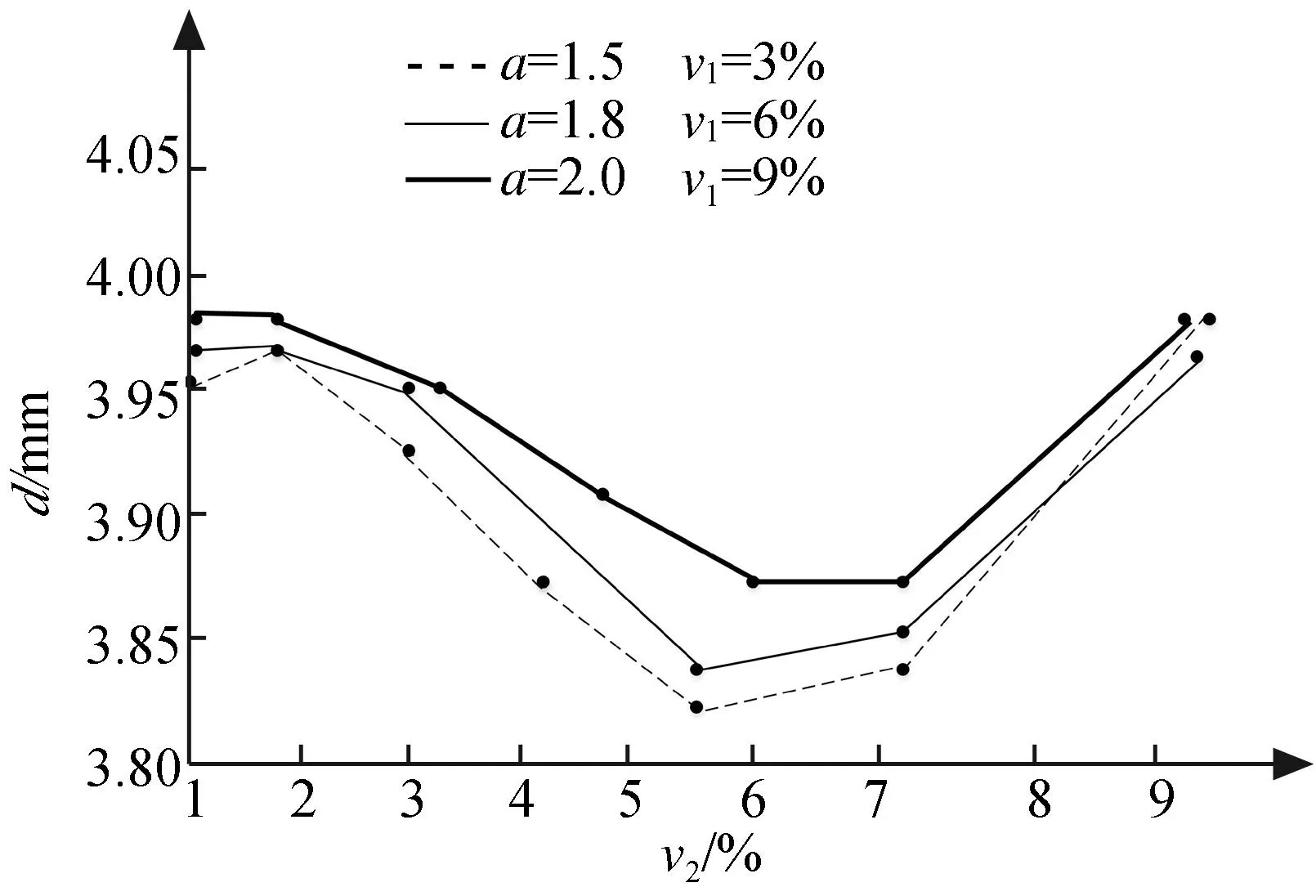
图4　探测速度对测头直径的影响

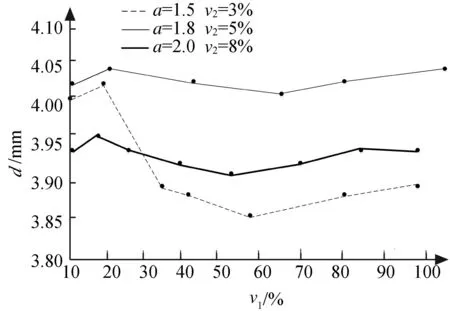
图5　移动速度对测头直径的影响

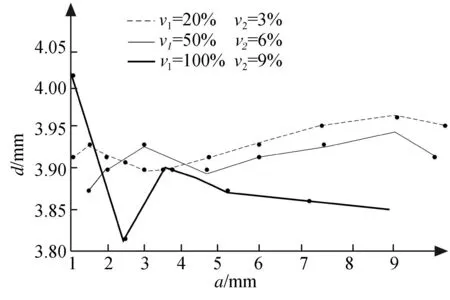
图6　临近距离对测头直径的影响

由图可知，DCC参数与测头直径d之间并非线性关系，在3个DCC参数中，对测头直径d影响最大的是临近距离a，影响最小的是测头移动速度v1。因此在测量机进行实际探测之前，务必确保使用的DCC参数与标准测头中的DCC参数保持一致[18]。

2)微平面补偿法。微平面补偿法，即在被测点P(xp,yp,zp)附近测得3个点P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)，然后用最小二乘法确定其最佳拟合平面及其法向矢量，从而对测头直径进行补偿(见图7)。

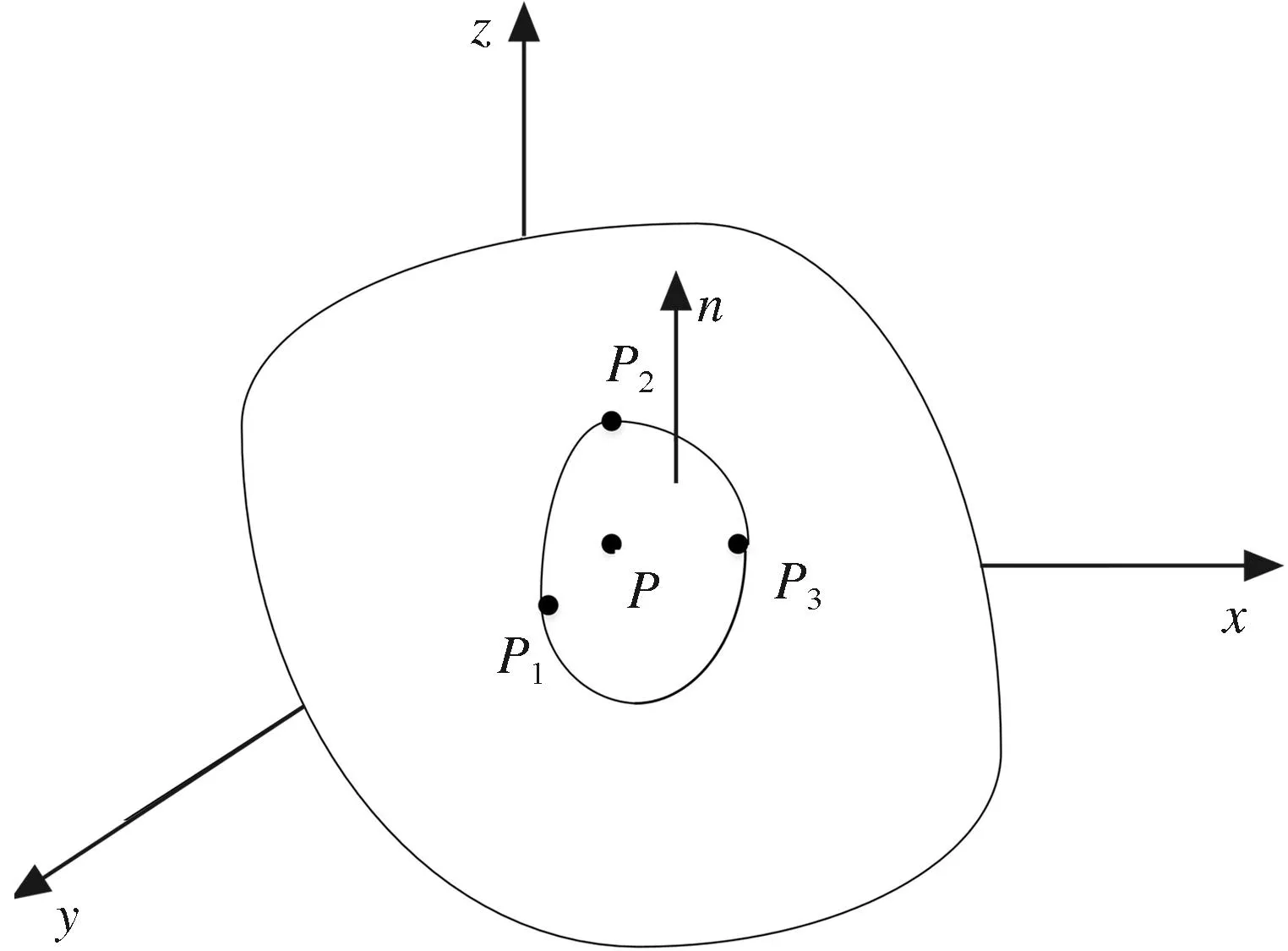
图7　微平面补偿简图

因为点P1，P2，P33个点是从点P的邻近区域所获取，所以将该4点组成的微平面法向矢量近似当作点P的法向矢量，记为n(x,y,z)，即

经过计算可求得点P(xp,yp,zp)的坐标为

式中：O(x0,y0,z0)为球心坐标；d0为测球直径。

微平面补偿法适合对复杂曲面自动测量，当测点较多时，可以通过计算机进行数据处理，得到被测点坐标，从而实现对测头直径的补偿。在测头进行工件测量时，先对测头进行直径动态标定，然后利用微平面补偿法对测头直径进行补偿。二者结合可以较大幅度提高测量机测头的测量精度。本文以改进型MC850三坐标测量机为测量工具，对某凹轮进行轮廓测量。

表1为三坐标测得凹轮轮廓的红宝石测球中心点的坐标以及经过测球直径标定和微平面补偿法二者补偿后被测轮廓点的坐标。其中，补偿后的点形成的轮廓线即为凹轮的实际轮廓。

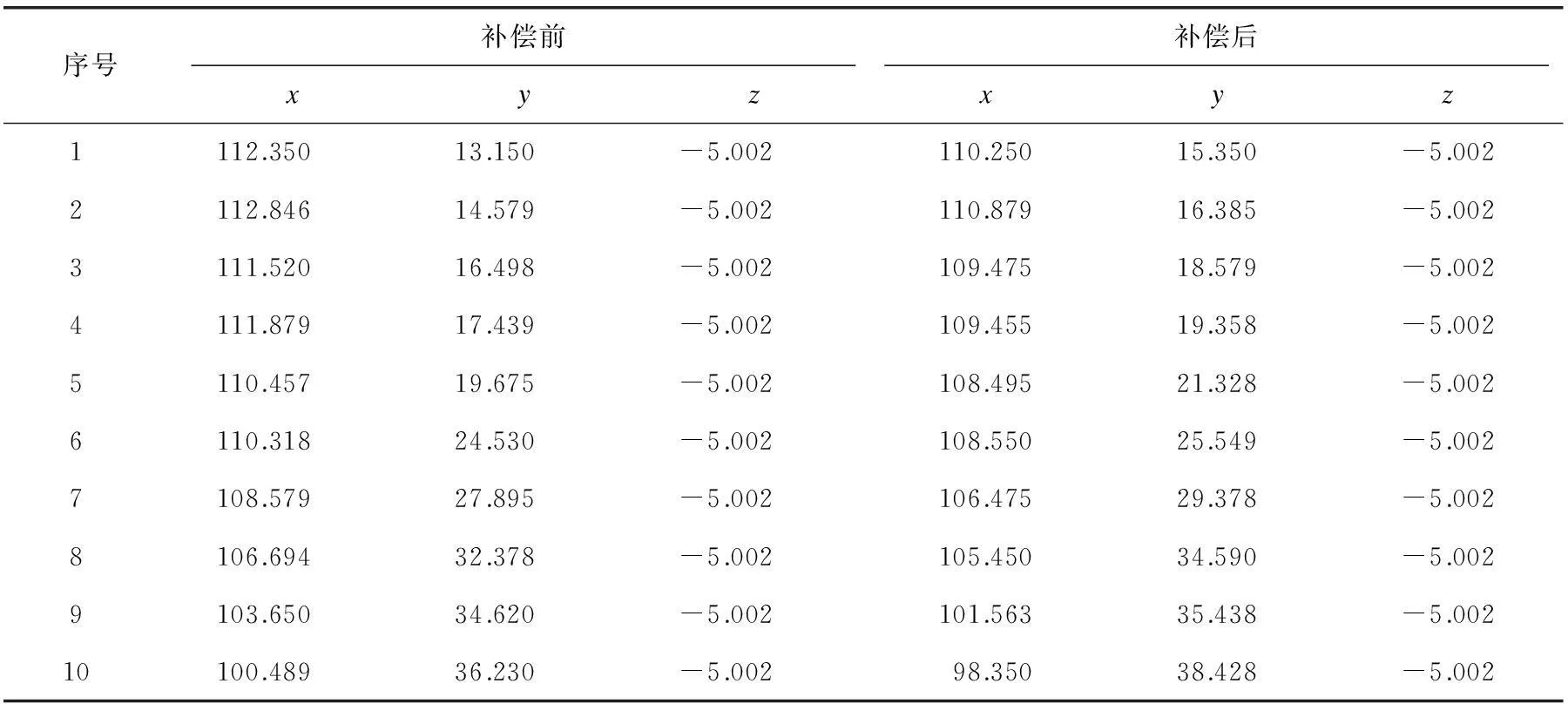
表1　测球中心点补偿前后的廓线坐标　mm

将以上数据读入逆向工程软件，得到该凹轮的测量轮廓线和实际轮廓线。通过将凹轮测量轮廓、实际轮廓与理论凹轮轮廓相比，可发现补偿后的凹轮轮廓更接近于理论轮廓，即提出的将测头直径动态标定与微平面补偿法相结合对测头测量误差有较好的补偿作用。

4结论

本文以三坐标测量机的触发式测头为研究对象，分析了测头预行程误差及影响因素，针对测头直径补偿，提出了将测头直径动态标定与微平面补偿法相结合的方法，其中在测头直径动态标定中讨论了不同运动参数DCC对测头直径动态标定的影响。

通过上述方法对凹轮进行轮廓测量，得到测量结果并与凹轮实际模型相对比，结果表明将测头直径动态标定与微平面补偿法相结合的方法能够对测头直径进行较好的补偿。但是，在测量数据中，存在个别数据与实际模型误差较大，需要进一步加以研究。

[参考文献]

[1]费业泰，赵静，王宏涛，等.三坐标测量机动态误差研究分析[J].仪器仪表学报，2004，25(S1):773-776.

[2]陈广良.三坐标测量中测头半径误差分析与修正方法[J].计量学报，2011，12(1):15-36.

[3]董晨松，穆玉海，张国雄.评定三坐标测量机的动态误差[J].中国机械工程，2012，9(7):200-239.

[4]KASASHIMA N，KURITA T.Laser and electrochemical complex machining of micro-stent with on-machine three-dimensional measurement[J].Optics and Lasers in Engineering，2012(3):354-358.

[5]杨洪涛，刘勇，费业泰，等.三坐标测量机动态误差混合建模方法[J].仪器仪表学报，2010，31(8):1861-1866.

[6]韩锋，田威，袁正茂，等.面向飞机大部件的智能三坐标辅助测量技术研究[J].中国机械工程，2015，35(6):223-249.

[7]盖宇春，朱伟东，柯映林.三坐标定位器部件刚度配制方法[J].浙江大学学报，2014,12(3):124-231.

[8]ACHICHE S，WOZNIAK A.Three-dimensional modeling of coordinate measuring machines probing accuracy and settings using fuzzy knowledge bases: Application to TP6 and TP200 triggering probes[J].Artificial Intelligence For Engineering Design Analysis And Manufacturing，2012，35(2):425-441.

[9]马修水.三坐标测量机动态误差源分析、建模与修正技术研究[D].合肥：合肥工业大学，2005.

[10]费业泰，卢荣胜.动态测量误差修正原理与技术[M].北京：中国计量出版社，2001.

[11]宋开臣，张奕群，李书和，等.三坐标测量机动态误差补偿的研究[J].仪器仪表学报，1999,20(1):23-25,59.

[12]LI D，CHEUNG C F，REN M,et al.Autostereoscopy-based three-dimensional on-machine measuring system for micro-structured surfaces[J].Optics Express，2014，24(3):25635.

[13]王恩双，徐连军.三坐标测头测量系统误差分析[J].科技创新与应用，2016，12(2):234-267.

[14]辇兴玲.移动桥式三坐标测量机结构设计与误差分析研究[D].哈尔滨:哈尔滨理工大学，2012.

[15]王晨晨.异端类型三坐标测量机结构原理及误差修正技术研究[D].合肥：合肥工业大学，2012.

[16]SONG K，ZHANG Y，LI S H，et al.A study of compensation for dynamic errors of CMMS[J].Chinese Journal of Scientific Instrument，1999，35(1):220-259.

[17]MURALIKRISHNAN B，STONE J，STOUP J.Performing three-dimensional measurements on micro-scale features using a flexible coordinate measuring machine fiber probe with ellipsoidal tip[J].Measurement Science and Technology，2012,23(4):249-367.

[18]张梅，费业泰，盛立.三坐标测量机测端动态有效作用直径影响因素分析[J].中国机械工程，2013,35(6):157-160.

责任编辑：陈亮

doi:10.3969/j.issn.1671-0436.2016.03.008

收稿日期：2016- 05- 06

基金项目：安徽省教育厅自然科学重点项目(KJ2015A058)

作者简介：杜翠翠(1991—)，女，硕士研究生。

中图分类号：TH-9

文献标志码：A

文章编号：1671- 0436(2016)03- 0033- 05

Error Analysis and Modification on the Probe System of Coordinate Measuring Machine

DU Cuicui,XU Qiang,FENG Xugang,ZHANG Jiayan

(College of Information and Electrical Engineering,Anhui University of Technology,Maanshan 243032)

Abstract：As probe is the key component of coordinate measuring machine (CMM),its dynamic performance has direct influence on the final measurements.In order to enhance the accuracy of CMM,composition of the probe dynamic error system was studied with focus on introducing the touch trigger probe.Probe pre-travel error sources and influencing factors were analyzed.The method combining dynamic calibration of probe radius and micro plane compensation was put forward to make compensation for the probe radius.After measuring the outline of a concave wheel and comparing probe radius before and after the compensation in reverse engineering software,the results showed that the method made better compensation for the probe radius and was worth more applications.

Key words：coordinate measuring machine;probe system;pre-travel error;diameter of probe