随机波动率下障碍期权定价的对偶MonteCarlo模拟

温　鲜，邓国和

(1.广西科技大学鹿山学院，广西柳州545616；2.广西师范大学数学与统计学院，广西桂林541004)



随机波动率下障碍期权定价的对偶MonteCarlo模拟

温鲜1，邓国和2

(1.广西科技大学鹿山学院，广西柳州545616；2.广西师范大学数学与统计学院，广西桂林541004)

摘要：为了克服经典BS模型隐含波动率的“微笑”效应，本文假定标的股票价格服从随机波动率模型，使之与市场价格更加符合，并应用对偶Monte Carlo模拟方差减小技术分别模拟出股价波动率过程和股票价格过程的路径，给出了欧式障碍期权定价的具体算法，求出了下降敲出欧式看涨障碍期权价格的估计量。最后，通过期权价格的二叉树数值解与近似公式解验证对偶Monte Carlo模拟数值解的准确性。

关键词：随机波动率；对偶Monte Carlo模拟；障碍期权

0引言

1973年Black和Scholes建立的期权定价公式Black-Scholes(BS)将股票价格表示为标的资产价格和一个常数波动率的函数，这与实际市场观测数据不符合。因此，经典的BS模型需要不断改进，使之与实际市场更符合，为投资者提供理论依据。因此本文研究随机波动率模型，即把标的资产(股票)价格的波动率也看作一个随机过程。国外，Hull和White[1]在(HW)随机波动率模型(相关系数ρ=0)下得到了标准欧式期权价格的近似解析公式；Heston[2]在Heston随机波动率模型(相关系数ρ≠0)下给出了债券和货币期权的封闭解。国内，对随机波动率模型的期权定价研究主要有：邓国和[3]应用离散快速Fourier变换法讨论了随机波动率跳扩散模型下美式期权和复合期权的数值计算问题；姜迪等[4-7]考虑了标的股价满足随机波动率模型的欧式期权、障碍期权、回望期权的定价；曹小龙[8]利用拟蒙特卡罗模拟技术进行了标准美式期权定价的数值计算方面的研究。

障碍期权是标的资产(股票)的价格路径受到一定的限制，是否有效取决于标的资产(股票)的价格是否触及确定的界限值(障碍值)，即是在一个普通期权基础上加上一个触发点。这种期权的主要目的是控制投资者的风险在一定范围之内。其中，敲出障碍期权是当标的资产(股票)价格达到一个障碍值时，该期权无效；敲入障碍期权是当标的资产(股票)价格达到一个障碍值时，该期权生效。关于障碍期权的定价首先由Merton[9]在标的资产(股票)价格满足随机波动率模型下得到了欧式障碍期权价格的解析解；而其他学者对障碍期权定价研究[10-11]仅局限在波动率为常数的情形下。近年来，国内得到了HW随机波动率模型的欧式障碍期权定价的近似解析解[5]。蒙特卡罗方法(MonteCarlo，MC)又称为随机模拟法，基本原理是运用抽样思想，将求解的问题转化为概率模型，并利用计算机软件进行随机模拟，得到求解问题的数值解。但运用普通MC模拟方法计算期权价格，有时会与实际值存在着大偏差，这时就需要用一些方差减小技术降低估计值的方差。因此，本文在标的股票服从随机波动率模型下(涵盖相关系数ρ=0与ρ≠0两种情形)，应用对偶MonteCarlo模拟法求出欧式下降敲出障碍期权价格的估计量，并进行数值计算。

1随机波动率模型

设金融市场中无摩擦、也没有套利存在，在投资期[0，T]内可以连续交易，投资者可以买空、卖空风险资产，也可以在无风险利率下进行任意存、借款。假设金融市场中有两种可交易的证券，其中B(t)为无风险证券，称为债券，其价格满足：

dB(t)=rB(t)dt，

(1)

r为无风险利率。另一种S为风险资产，称为股票，其价格过程S(t)及其波动率过程Y(t)，在风险中性概率测度P下，满足如下的随机微分方程：

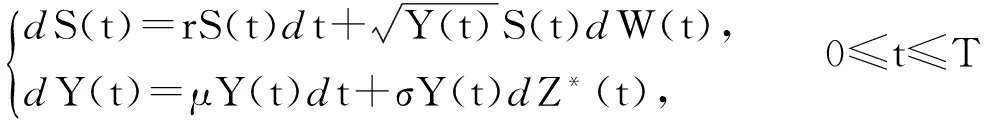
(2)

其中W(t)、Z*(t)都是风险中性概率测度P下的标准布朗运动，且

Cov(dW(t)，dZ*(t))=ρdt，

(3)

(4)

2对偶MonteCarlo(MC)模拟的障碍期权定价

对于障碍期权价格的数值计算本文主要以下降敲出欧式看涨障碍期权为例，同理也可以讨论其他类型障碍期权的定价研究，具体算法过程如下：

2.1波动率过程{Y(t)，0≤t≤T}的MonteCarlo(MC)模拟

由模型(4)，股票价格波动率过程Y(t)满足如下随机微分方程：

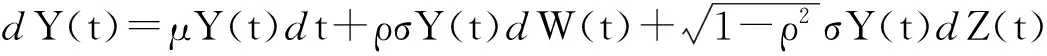
(5)

其中Z(t)与W(t)是相互独立的布朗运动，ρ为确定的常数，那么

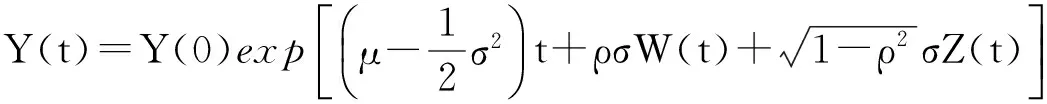
(6)

⋮

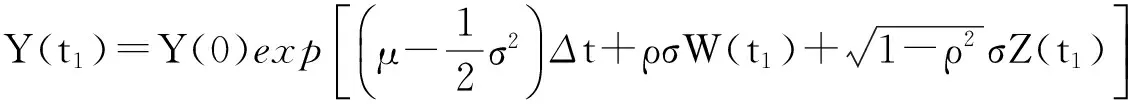
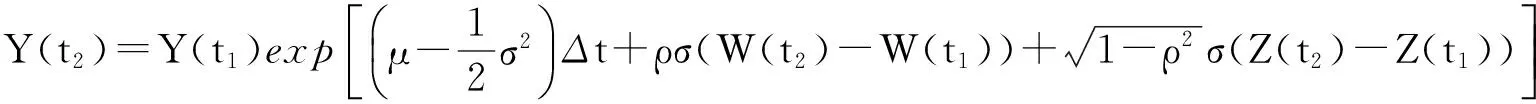
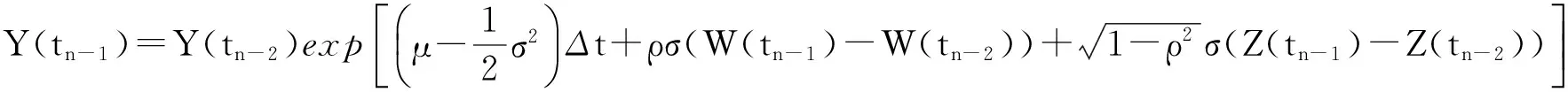
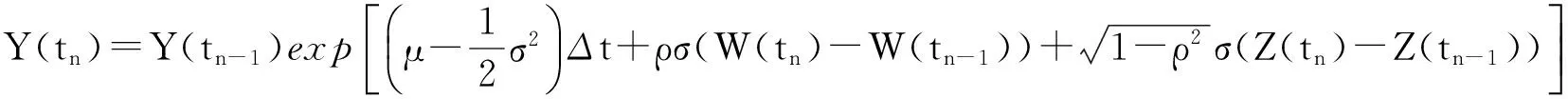
而W(t1)-W(t0)，W(t2)-W(t1)，…，W(tn)-W(tn-1)与Z(t1)-Z(t0)，Z(t2)-Z(t1)，…，Z(tn)-Z(tn-1)是两组相互独立的增量，且W(ti)-W(ti-1)～N(0，Δt)，Z(ti)-Z(ti-1)～N(0，Δt)，i=1，2，…，n。因此首先可由Matlab软件模拟两组相互独立且服从标准正态分布N(0，1)的n×m维随机向量，分别记为A、B，利用公式

以及A、B可模拟W(ti)-W(ti-1)和Z(ti)-Z(ti-1)，i=1，2，…，n。其中A=(a1，a2，…，an)′，B=(b1，b2，…，bn)′，且ai=aij，bi=bij，i=1，2，…，n，j=1，2，…，m。于是可求：

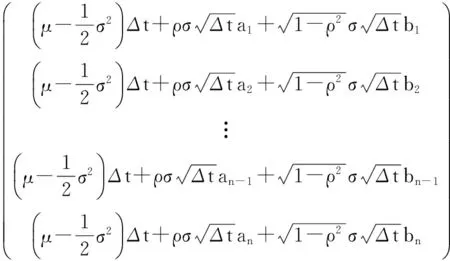
对Y(ti)(i=0，1，2，…，n)取对数，有：

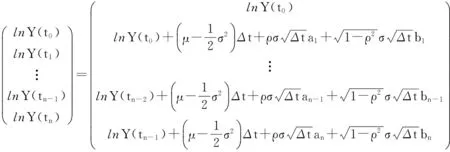
(7)

对式(7)左右两边的元素取指数，则可得到Y(t)在[0，T]内的m次MC模拟：

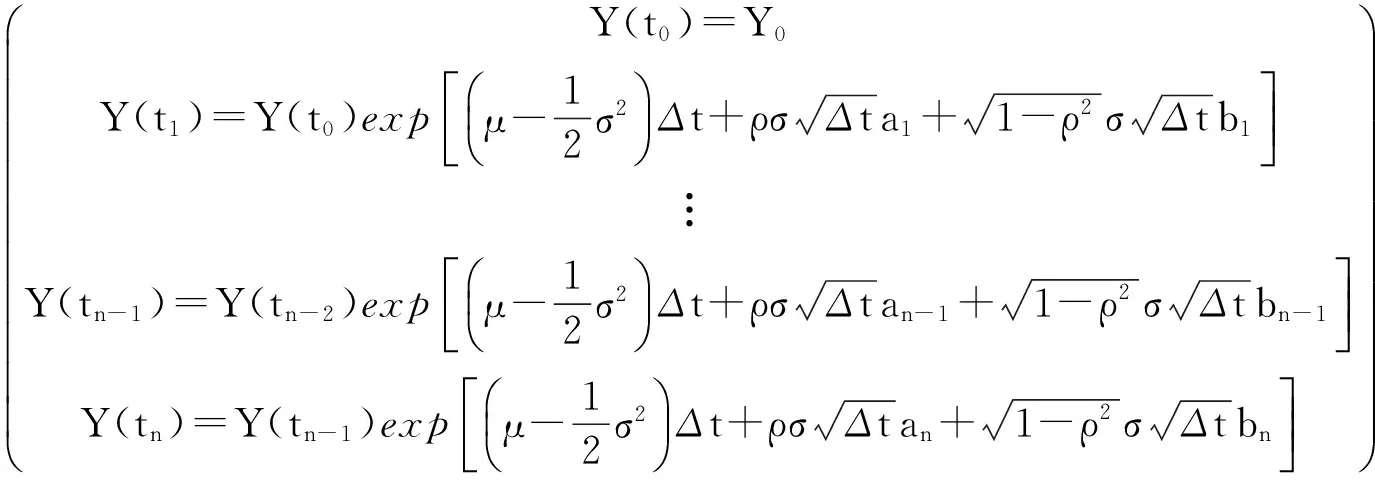
2.2股票价格过程{S(t)，0≤t≤T}的对偶MonteCarlo(MC)模拟

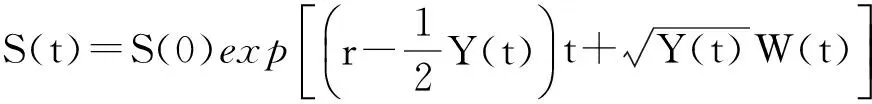
(8)

对时间区间[0，T]作同上的分割，有：

而W(t1)-W(t0)，W(t2)-W(t1)，…，W(tn)-W(tn-1)是相互独立的增量，且W(ti)-W(ti-1)～N(0，Δt)，其中i=1，2，…，n。同理利用Matlab软件模拟服从标准正态分布N(0，1)的n×m维向量，记为C，其中C=(c1，c2，…，cn)′，且ci=cij，i=1，2，…，n，j=1，2，…，m。利用

可模拟W(ti)-W(ti-1)，i=1，2…，n。

于是可模拟下列向量

对S(ti)(i=1，2，…，n)取对数，有：

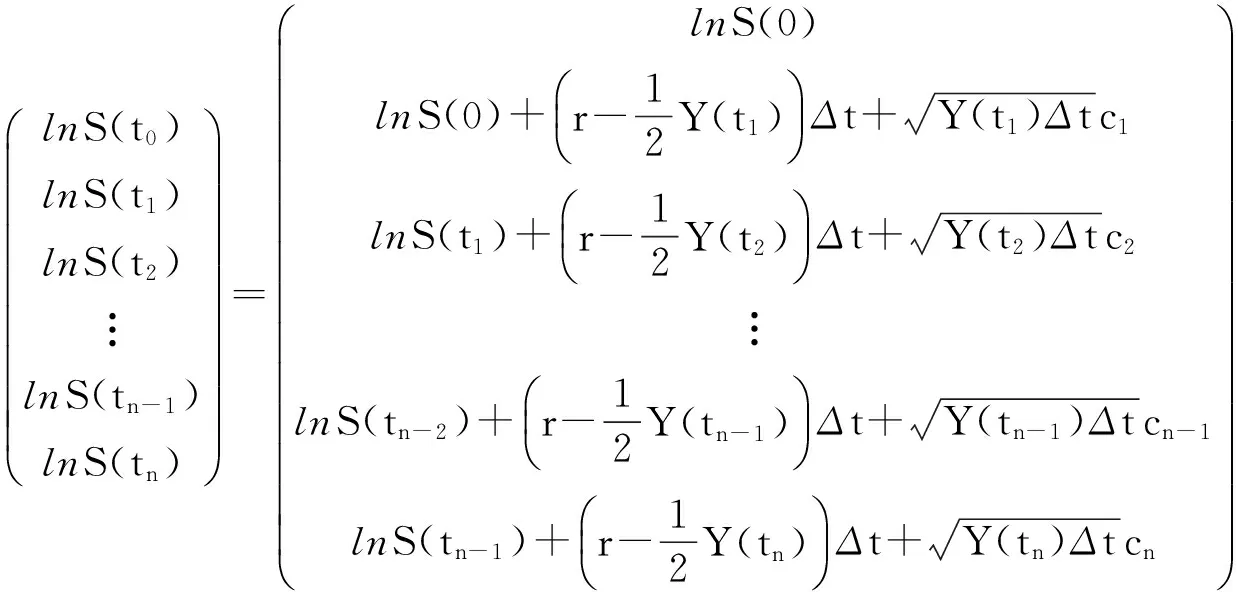
(9)

对式(9)中的元素左右两边取指数，则得到股票价格S(t)在[0，T]内的m次MC模拟路径：

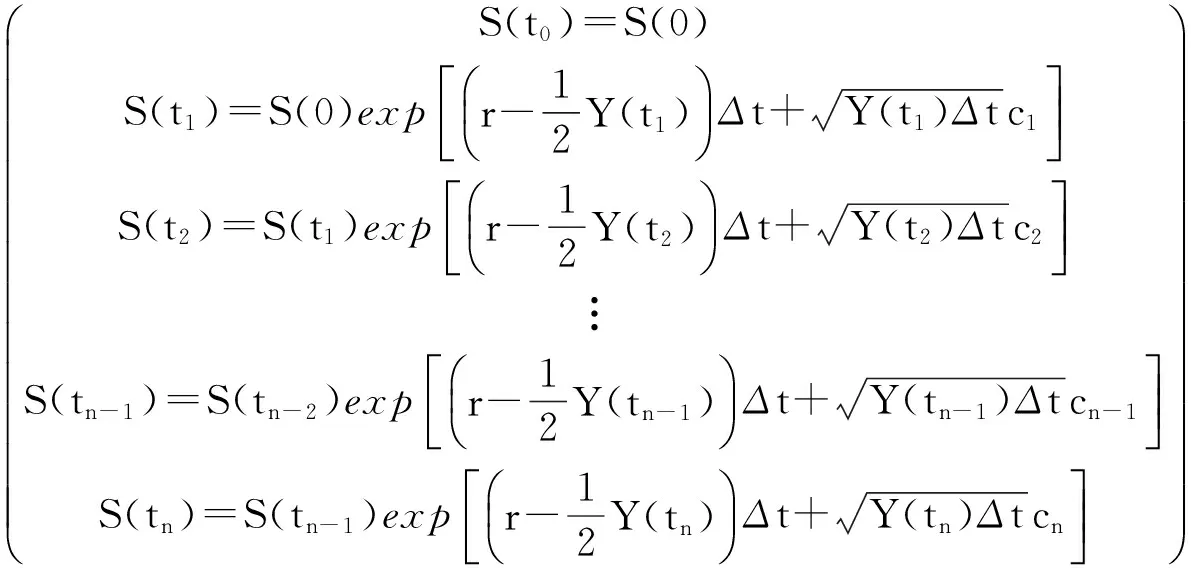
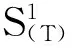
其中-C=(-c1，-c2，…，-cn)′，且-ci=-cij，i=1，2，…，n，j=1，2，…，m。于是：

对S(ti)(i=1，2，…，n)取对数，有：

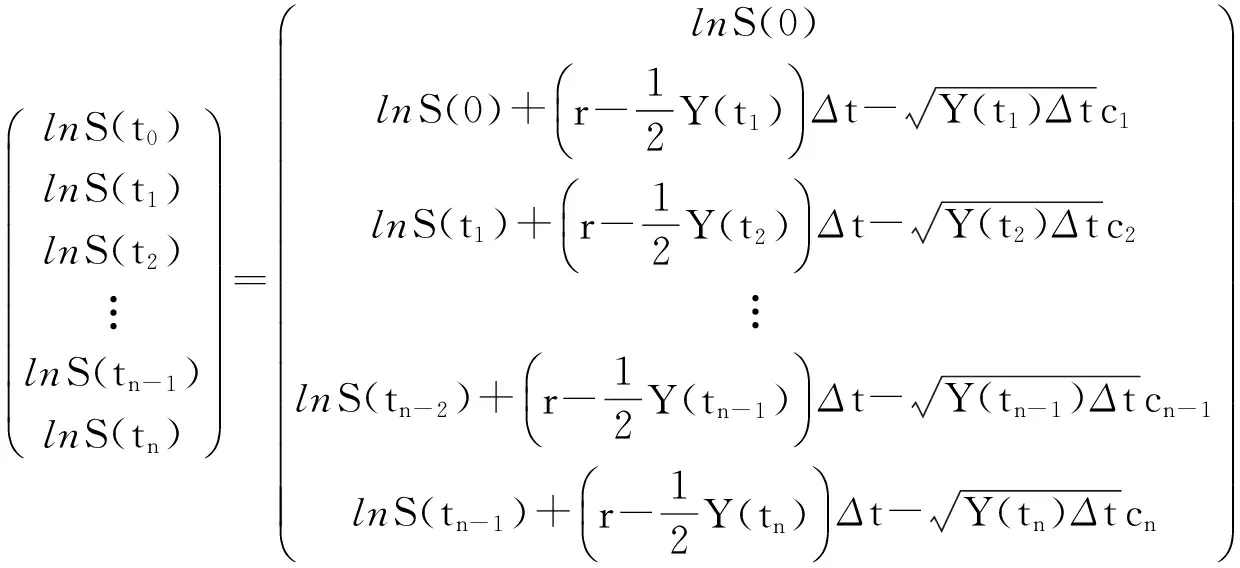
(11)

对式(11)中的元素左右两边取指数，则得到股票价格S(t)在[0，T]内的m次对偶MC模拟路径：

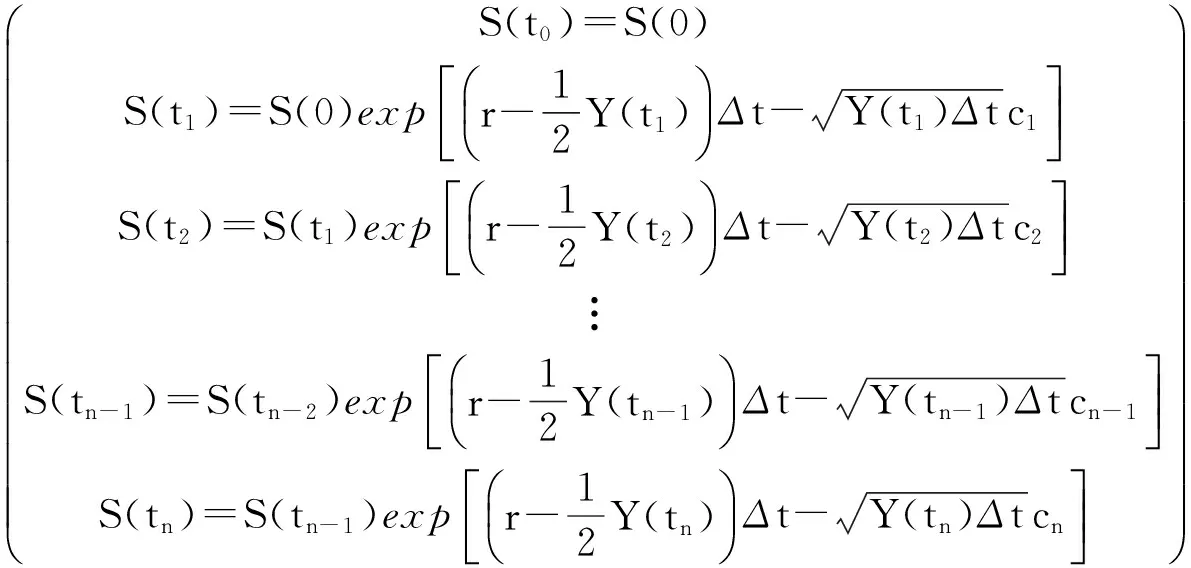
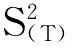
2.3期权价格对偶MonteCarlo模拟

由期权的收益函数可以知道，利用对偶MC方差减小技术模拟得出的m次股票价格路径， 可以计算各类欧式障碍期权的价格，本文以下降敲出欧式看涨障碍期权定价为例。

定理1标的资产(股票)价格过程S(t)及其波动率过程Y(t)满足模型(4)，则由m次模拟所得到下降敲出欧式看涨障碍期权在时刻t∈[0，T]的价格估计量为：

(12)

3数值结果和分析

图1　对偶MC模拟股票价格Fig.1　The dual variables techniques for Monte Carlo simulation of stock prices

首先，结合模型(4)，通过对偶MC模拟法模拟股票价格变化趋势见图1。基本参数值为：S0=100；μ=0；r=0.05；H=90；σ=0.1；K=95，100，105；Y(0)=0.02，0.05。其中Y(0)为股票价格波动率的初始值。

其次，利用对偶(MC)模拟的股票价格计算下降敲出欧式看涨期权的价格，并利用近似解析式、二叉树法验证对偶(MC)模拟法计算期权价格的准确性与有效性，见表1、2。表1中，应用近似解析式[5]、二叉树法[7]与对偶(MC)模拟法求解模型(4)(ρ=0)的障碍期权价格进行了比较。表2比较了二叉树法、对偶(MC)模拟法在模型(4)中(相关情形(ρ≠0))的障碍期权价格的数值计算结果。由表1、2可以看出，对偶(MC)模拟算法具有很好的准确性，相同条件下，相关情形的期权价格比独立情形期权价格高。由表2可以看出，当波动率初始值为给定常数，障碍期权的期权随着执行价格K逐渐增大而减小，随着交易时间的逐渐增大而增大；当其他参数给定时，期权价格值随着相关系数ρ的增大而减小。

表1　 近似公式解、二叉树法、对偶MC模拟法计算期权价格的比较(ρ=0)

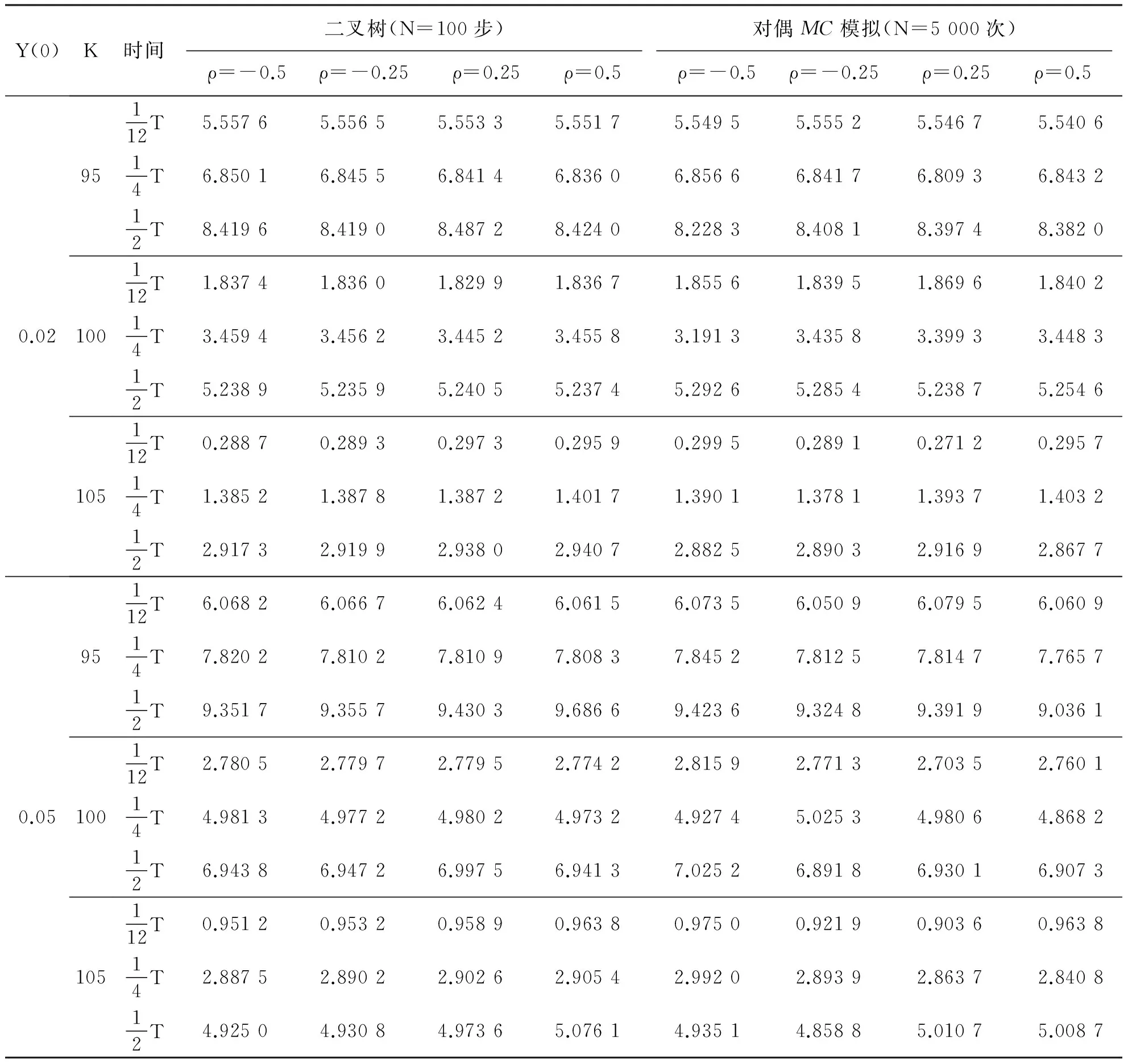
表2　二叉树法、对偶MC模拟法计算期权价格的比较(ρ≠0)

4结论

本文利用对偶(MC)模拟原理给出随机波动率模型(4)下的欧式障碍期权定价的具体数值算法，并求出下降敲出欧式看涨障碍期权价格的估计量(12)，涵盖了模型(4)中相关系数ρ=0与ρ≠0两种情形。其他类型欧式障碍期权价格的估计量也可类似求解。文献[5]中求出模型(4)中相关系数ρ=0情形下欧式障碍期权价格的近似解析解，而本文是文献[1]的推广，利用对偶(MC)模拟方差减小技术研究随机波动率模型下(相关系数ρ=0与ρ≠0情形)欧式障碍期权价格的数值计算。

在数值计算实例中，首先应用近似公式法[5]、二叉树法[7]、对偶(MC)模拟法分别计算欧式障碍期权的价格，并利用计算结果验证了对偶(MC)模拟计算欧式障碍期权价格的准确性。

基于对偶(MC)模拟法研究模型(4)的欧式障碍期权价格，考虑其他方差减小技术，也可以进一步研究模型(4)下美式障碍期权价格的数值计算。

参考文献：

[1]HULLJC,WHITEA.Thepricingofoptionsonassetswithstochasticvolatilities[J].JournalofFinance，1987，42(2)：281-300.DOI:10.1111/j.1540-6261.1987.tb02568.x.

[2]HESTONSL.Aclosed-formsolutionforoptionswithstochasticvolatilitywithapplicationstobondandcurrencyoptions[J].ReviewofFinancialStudies，1993，6(2)：327-343.DOI:10.1093/rfs/6.2.327.

[3]邓国和.随机波动率跳跃扩散模型下复合期权定价[J]. 数理统计与管理，2015，34(5)：910-922.DOI:10.13860/j.cnki.sltj.20140311-001.

[4]姜迪，王玉文.随机波动率模型下的欧式期权定价[J]. 哈尔滨师范大学自然科学学报，2015，31(3)：38-41.

[5]温鲜，邓国和，霍海峰.Hull-White随机波动率模型的欧式障碍期权[J].广西师范大学学报(自然科学版)，2009，27(4)：49-52.DOI：10.16088/j.issn.1001-6600.2009.04.004.

[6]徐蕾，邓国和.随机波动率模型下欧式回望期权定价[J].广西师范大学学报(自然科学版)，2015，33(3)：79-90.DOI:10.16088/j.issn.1001-6600.2015.03.013.

[7]陈俊霞，蹇明.随机波动率情形下期权定价的解析解[J].统计与决策(理论版)，2007(8)：21-22.DOI:10.13546/j.cnki.tjyjc.2007.08.008.

[8]曹小龙，胡云姣. 美式期权定价的拟蒙特卡罗模拟及其方差减小技术[J].北京化工大学学报(自然科学版)，2014，41(3)：119-124.DOI：10.13543/j.cnki.bhxbzr.2014.03.022.

[9]BLACKF,SCHOLESM.Thepricingofoptionsandcorporateliability[J].JournalofPoliticalEconomy，1973，81(3)：637-654.

[10]SCHOBELR，ZHUJianwei.StochasticvolatilitywithanOrnstein-Uhlenbeckprocess：Anextension[J].EuropeanFinanceReview，1999，3(1)：23-46.DOI:10.1023/A:1009803506170.

[11]RUBINSTEINM.Impliedbinomialtrees[J].JournalofFinance， 1994，49(3)：771-818.DOI:10.1111/j.1540-6261.1994.tb00079.x.

[12]姜礼尚.期权定价的数学模型和方法[M].北京：高等教育出版社，2003.

(责任编辑黄勇)

doi:10.16088/j.issn.1001-6600.2016.02.013

收稿日期：2015-09-09

基金项目：国家自然科学基金资助项目(11461008)；2014年广西高等教育教学改革重点项目(2014JGZ192)；广西科技大学鹿山学院转型发展专项项目(2015ZXZD004)

中图分类号：O211.6；F830.9

文献标志码：A

文章编号：1001-6600(2016)01-0090-08

MonteCarloSimulationswithDualVariablesPricingofBarrierOptionsinaStochasticVolatilityModel

WENXian1，DENGGuohe2

(1.LushanCollege,GuangxiUniversityofScienceandTechnology，LiuzhouGuangxi， 545616,China；2.CollegeofMathematicsandStatistics，GuangxiNormalUniversity，GuilinGuangxi， 541004,China)

Abstract:In order to overcome the "smile" effect of the implied volatility of the stock market price and to make it fit with the market price, the pricing problem of an European barrier option is considered in stochastic volatility model. The pricing algorithm of European barrier option, the path of the volatility process and the path of the stock price are given by using the dual variable method. Then, the estimator of this option is provided. Finally, numerical examples using the finite difference method are provided to verify the accuracy of using Monte Carlo simulation with dual variable techniques.

Keywords:stochastic volatility； dual variable technique； barrier option

通信联系人：邓国和(1969—)，男，湖南桂阳人，广西师范大学教授，博士。E-mail:dengguohe@mailbox.gxnu.edu.cn