自动化集装箱码头成组直接中转的岸桥作业调度

周秀丹，胡志华，魏　晨

(上海海事大学物流研究中心，上海201306)



自动化集装箱码头成组直接中转的岸桥作业调度

周秀丹，胡志华，魏晨

(上海海事大学物流研究中心，上海201306)

摘要：本文针对自动化集装箱码头成组直接中转情况下岸桥的调度问题，研究了中转完工时间、岸桥等待时间、集装箱组数之间的关系。首先，以最小化中转完工时间建立了优化模型；接着，在此基础上以最小化中转完工时间和岸桥的等待时间为目标建立了多目标模型。通过多组算例研究，获得在集装箱组数不同的情况下中转完工时间及集装箱组开始装卸时间，并分析了集装箱组数的设置对中转完工时间、岸桥等待时间带来的影响。拓展了岸桥调度的研究，为集装箱码头运营提供了岸桥调度的参考。

关键词：集装箱码头；成组策略；直接中转；岸桥作业调度

0引言

近年来，随着世界贸易和集装箱运输业的发展，集装箱船的装载量和达港频率稳步增加，进而促使集装箱码头向大型化、自动化转型。如何在转型的过程中提高集装箱码头运作效率是一个值得研究的议题[1-2]。因此，很多学者从不同的角度对集装箱码头的运作进行了研究。首先，在集装箱场内堆存优化方面，Wu等[3]建立了混合整数规划模型和非混合整数规划模型来解决集成方式下集装箱堆放问题，并对两个模型的结果进行了对比。Tsai等[4]对混堆模式的集装箱码头堆场空间资源配置优化问题进行了研究，分别以平衡各箱区贝位间的作业量和最小化泊位到堆场的运输距离为优化目标，建立了两阶段优化模型。Tierney等[5]以最小化集装箱堆放容量和翻箱时间为目标，用启发式算法求解不同堆放原则下集装箱堆存顺序。Carlo等[6]则对集装箱码头堆场使用的设备及堆场的分类方案、发展趋势进行了阐述。毛钧等[7]以平衡各箱区泊位的作业量和最小化集装箱到堆场的运输距离为目标，建立了两阶段模型。魏航[8]提出了码头方补助金函数与车辆方的成本函数，建立了取箱时间窗优化模型，并设计了遗传算法对集装箱堆放模型进行求解。其次，由于各项科技的发展，集装箱码头在工艺设计方面也有了极大的突破。孙凯等[9]基于船舶大型化这一趋势对集装箱码头前沿操作工艺进行了研究。林浩[10]、郑见粹等[11]对自动化集装箱码头的装卸工艺方案及技术特点进行了全面的分析和对比。最后，在岸桥调度方面，邢曦文等[12]考虑集装箱码头现实作业中预定义顺序、避免岸桥交叉作业、以及取决于作业顺序的切换时间等现实约束，针对集装箱装卸作业的特点，设计了两阶段启发式算法。范志强等[13]考虑岸桥作业不可相互穿越与安全距离等特有约束， 以最小化最大完工时间与等待时间为目标，建立了岸桥作业调度双目标混合整数规划模型。Zhang等[14]以最小化岸桥的数量为目标，建立了一个整数规划模型，并采用混合式启发算法对其进行求解。Diaba[15]、Theodorou等[16]分别利用拉格朗日松弛法、遗传算法对岸桥的分配和集成调度模型进行求解。Nguyen[17]、Izquierdo等[18]分别借助混合进化算法和混合分布估计算法求解岸桥的调度计划模型。Kaveshgar[19]、Homayouni等[20]利用遗传算法就岸桥的调度问题进了行研究。Lee等[21]创新地提出用数学公式算法来解决岸桥的单向集成调度问题。从以上文献来看，虽然有关集装箱码头堆存方法、新型工艺、岸桥调度方面的研究有较多，但研究基于成组中转方式的岸桥调度的文献很少。本文以自动化集装箱中转码头为背景，探讨基于成组直接中转方式的岸桥调度问题。

成组直接中转方式的显著特点是岸桥以成组的作业方式对集装箱进行装卸，并且在中转过程中集装箱不进入堆场。即集装箱从一程船(针对某一中转箱而言，将该箱从起始港运至中转港的船舶)上卸下后由二程船(针对某一中转箱而言，将该箱从中转港载运至目的港的船舶)直接运往目的港。鉴于集装箱船上有多个贝位，每个贝位中可能有多组集装箱，每一组集装箱到达的目的港是相同的，便可以考虑岸桥完成同一个集装箱组的所有集装箱装卸作业才开始对下一个组进行装卸，即以成组的方式对集装箱进行作业。成组直接中转的方式不仅有利于二程船上集装箱的有序装载，而且有利于简化一程船上岸桥的调度过程。

本文以自动化集装箱码头为研究背景，从完工时间最小和岸桥等待时间最小两个角度分别建立混合整数规划模型，采用CPLEX对模型进行求解，得出岸桥的调度计划并对不同规模的集装箱组的实验结果进行分析。考虑岸桥以成组作业的方式，并针对这一问题从不同的角度建模是本文的创新之处。

1问题分析

集装箱直接中转流程主要分为3个过程。首先，岸桥将集装箱从一程船上卸下；然后，AGV将集装箱运至二程船岸桥下；最后，岸桥将集装箱装载到二程船上，具体过程见图1。相对图2，可以看出在该作业模式下，集装箱无需进入堆场，因此相对传统作业模式从某种角度上简化了中转流程，节省中转时间，这对于场地短缺的码头来说意义尤其重大。

图1　自动化集装箱码头成组直接中转的岸桥作业调度过程Fig.1　The process of quay crane scheduling considering group-based strategy and direct transshipment at automated container terminal

由于在集装箱直接中转作业中装船和卸船过程基本是同步进行的，这就需要更多地考虑到多条船之间的同步性，因此，集装箱直接中转码头的作业对一程船(从起运港发出的船)和二程船(目的港船舶)到港的时间有了更加严格的要求。同时，集装箱直接中转码头通常要求整个作业完工时间可以达到最小，这就容易出现岸桥在未完成对当前集装箱组的作业，而来自另一贝位中的集装箱已在等待其对它进行作业的情况，导致AGV在岸桥下停留时间过长，引起路面拥堵。此外，鉴于集装箱是以成组的方式进行装卸，即同一贝位的作业只能由同一台岸桥完成，且只有完成该贝位的作业后，岸桥才能移至下一贝位，而岸桥在贝位之间的移动时间相对装卸时间较短，故在整个装卸作业过程中岸桥的位置可视为不变。对此，在中转过程中需要对集装箱组开始装卸时间进行合理的规划，求得整个中转完工时间。

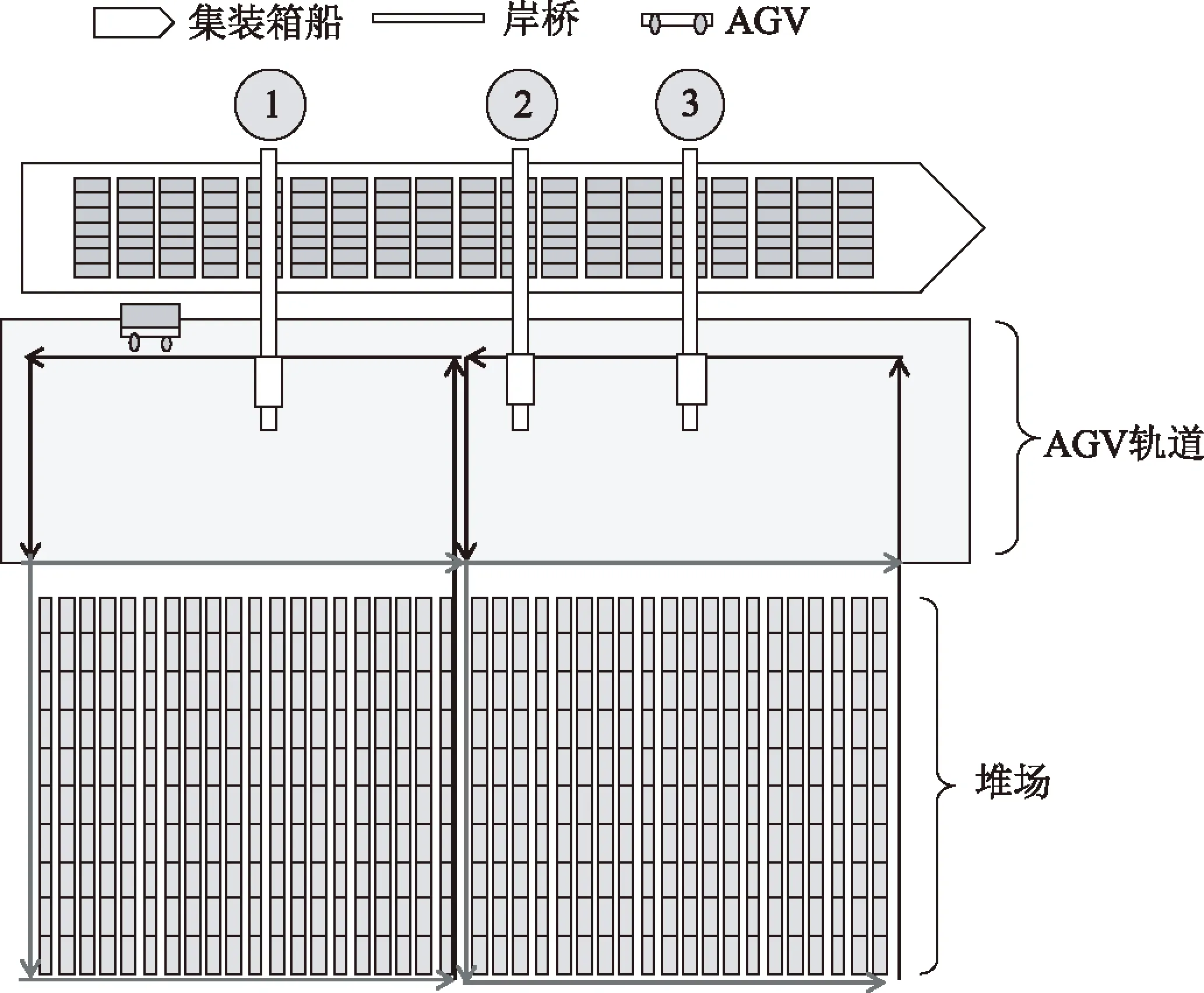
图2　自动化集装箱码头中转的岸桥作业调度过程Fig.2　The process of quay crane scheduling at automated container transfer terminal

2模型描述与构建

本文从不同的优化角度分别建立了模型，包括以最小化中转完工时间为目标的混合整数规划模型和以最小化中转完工时间和岸桥的等待时间为目标的规划模型。由此分别来讨论集装箱组数、完工时间、岸桥等待时间之间的关系。针对所建立的模型，本文作了如下假设：

假设1各岸桥作业能力之间没有差别。

假设2为保证安全作业，相邻的岸桥需保持一定的距离。并且，各岸桥位于同一轨道上，相互之间不能穿越。

假设3岸桥在贝位间移动时间相对装卸时间较小，因此予以忽略。

假设4集装箱在一程船和二程船上的位置已知。

2.1以最小化中转完工时间为目标的岸桥调度模型

本节要解决的问题是在不考虑岸桥的等待时间这样一个前提条件下，对每个集装箱组的开始作业时间进行规划，在以岸桥下无拥堵情况等约束下，建立以最小化中转完工时间为目标的混合整数规划模型。

2.1.1集合与参数

1)N：集装箱组集合。

2)Q：岸桥集合。

3)QUnload：负责将集装箱组从一程船上卸下的岸桥集合。

4)QLoad：负责将集装箱组装载到二程船上的岸桥集合。

5)Um：通过岸桥m卸载的集装箱组集合，m∈QUnload。

6)Ln：通过岸桥n装载的集装箱组集合，n∈QLoad。

7)Tm，n：集装箱组从岸桥m运往岸桥n的时间；

8)TUnload：岸桥卸载一个集装箱的时间。

9)TLoad：岸桥装载一个集装箱的时间。

10)Ai：第i个集装箱组中集装箱的数量。

11)M：足够大的正数，至少大于整个中转完工时间的最小值。

2.1.2决策变量

1)xi：集装箱组i开始卸载的时间。

2)yi，集装箱组i开始装载的时间。

3)xij，集装箱组j卸载完工之后到下一个集装箱组i开始卸载之间的时间间隔。

4)yij，集装箱组j装载完工之后到装载下一个集装箱组i之间的时间间隔。

5)ui，j∈{0，1}：如果集装箱组i紧接着组j卸载，ui，j为1，否则为0。

6)li，j∈{0，1}：如果集装箱组i紧接着组j装载，li，j为1，否则为0。

7)t：中转任务完成总时间。

8)tw1：岸桥的等待时间。

9)Ci，m，n∈{0，1}：如果集装箱组i由岸桥m卸载，岸桥n装载，Ci，m，n为1，否则为0。

2.1.3目标及约束

集装箱直接中转要求一程船和二程船在港靠泊的时间尽可能短，集装箱组装卸完工时间从一定程度上代表船的离港时间。由于将同一贝位中的一组集装箱作为一个调度任务(一组连续的卸载操作)，在卸载调度任务的过程中，当有两个任务需同时要求同一台岸桥对其进行装载作业时，将出现重载AGV在支线船停留，引起路面的拥堵。针对这些实际情况，模型的目标及约束如下：

[M1]minimizef1=t。

(1)

s.t.xi≥xj+Aj·ui，j·TUnload+(ui，j-1)·M，i，j∈Um，m∈QUnload，i≠j；

(2)

yi≥xi+TUnload+Ci，m，n·Tm，n，i∈N，m，n∈Q；

(3)

yi≥yj+TLoad+(Aj-1)·TUnload·li，j+(li，j-1)·M，i，j∈Ln，i≠j；

(4)

xij≥(xi-(xj+AjTUnload))+(uij-1)M；

(5)

yij≥(yi-(yj+(Aj-1)TUnload+TLoad))+(lij-1)M；

(6)

tw1=∑ij(xij+yij)；

(7)

ui，j+uj，i≤1，i，j∈Um，i≠j；

(8)

∑j∈Umui，j=1，i，j∈N；

(9)

∑i∈Umui，j-uj，j≤1，i，j∈Um；

(10)

∑i∈Umui，i=1；

(11)

li，j+lj，i≤1，i，j∈Ln，i≠j；

美观化，所谓爱美之心，人皆有之，在选购家电时自然也不例外。奥维云网（AVC）监测数据显示，象征美感的曲面、超轻薄、无边框彩电，彩晶面板冰箱，超薄洗衣机，艺术柜机空调，侧吸式油烟机，以及玻璃台面燃气灶等产品在2017年都取得了长足的发展。

(12)

∑j∈Lnli，j=1，i∈Ln；

(13)

∑i∈Umli，j-lj，j≤1，i，j∈Ln；

(14)

∑i∈Lnli，i=1；

(15)

t≥yi+TLoad+(Ai-1)·TUnload，i∈N；

(16)

xi≥0，i∈N；

(17)

xij，yij≥0。

(18)

目标函数定义为集装箱组装载完工时间的最小化，如式(1)所示。约束条件通过式(2)～(18)定义。式(2)为相邻卸载组i与组j之间的时间约束，其中Aj·ui，j·TUnload表示组j的卸载时间，组i与组j属于同一卸载岸桥m；式(3)表示组i的开始卸船时间与开始装船时间的关系，Ci，m，n·Tm，n表示集装箱从卸载岸桥m到装载岸桥n的运输时间；式(4)同式(2)，表示相邻装载组i与组j之间的时间约束；式(5)表示从卸载完集装箱组j到开始卸载下一个任务i之间时间间隔等于卸载完集装箱组j到开始卸载集装箱组i之间的时间间隔；式(6)表示从装载完集装箱组j到开始卸载下一个任务i之间时间间隔等于卸载完集装箱组j到开始装载集装箱组i之间的时间间隔；式(7)表示在整个中转过程中岸桥的等待时间之和；式(8)～(11)表示卸载组i与组j之间的相邻逻辑关系，式(8)表示组i在组j之前完成或组j在组i之前完成，式(9)表示组i必须在另一个任务之后完成(或者与相邻，表示组i为首任务)，式(10)表示组i仅且仅与另一个组相邻，式(11)表示在一个岸桥中，首任务出现且仅出现一次；式(12)～(15)同理可得，表示装载组i与组j之间的相邻关系；式(16)表示最大完成时间大于每一个集装箱组的最终完成时间；式(17)表示开始时间需大于0；式(18)表示时间间隔大于0。

2.2以中转完工时间和岸桥等待时间为目标的岸桥调度模型

仅以最小化转运完工时间为标准对岸桥作业调度进行衡量，忽略了岸桥作业效率对中转成本及岸桥在多条船之间进行相互支援这一现实情况，存在一定的局限性。因此，在[M1]的基础上，模型[M2]引入岸桥等待时间这一目标。[M2]将目标函数改为最小化中转完工时间和岸桥的等待时间，如式(19)所示。其中：λ1、λ2分别为中转完工时间和岸桥等待时间的权重，取值范围为0到1之间；tw2为岸桥的等待时间。此模型目的在于研究具有最小化完工时间与岸桥等待时间双目标的岸桥作业调度问题。

[M2]minimizef2=λ1t+λ2tw2，tw2=∑ij(xij+yij)，

(19)

s.t.式(2)～(18)，λ1，λ2∈(0，1)。

(20)

3算例

为了验证模型的正确性和有效性，本文采用某集装箱港口数据进行分析。该集装箱港口的总岸桥数为6个，集装箱组数为9，集装箱组中的集装箱的数量、负责卸载及装载每个集装箱组的岸桥及从卸载岸桥到装载岸桥的运输时间如表1所示。同时，岸桥卸载及装载一个集装箱到AGV上的时间分别为90s和60s。

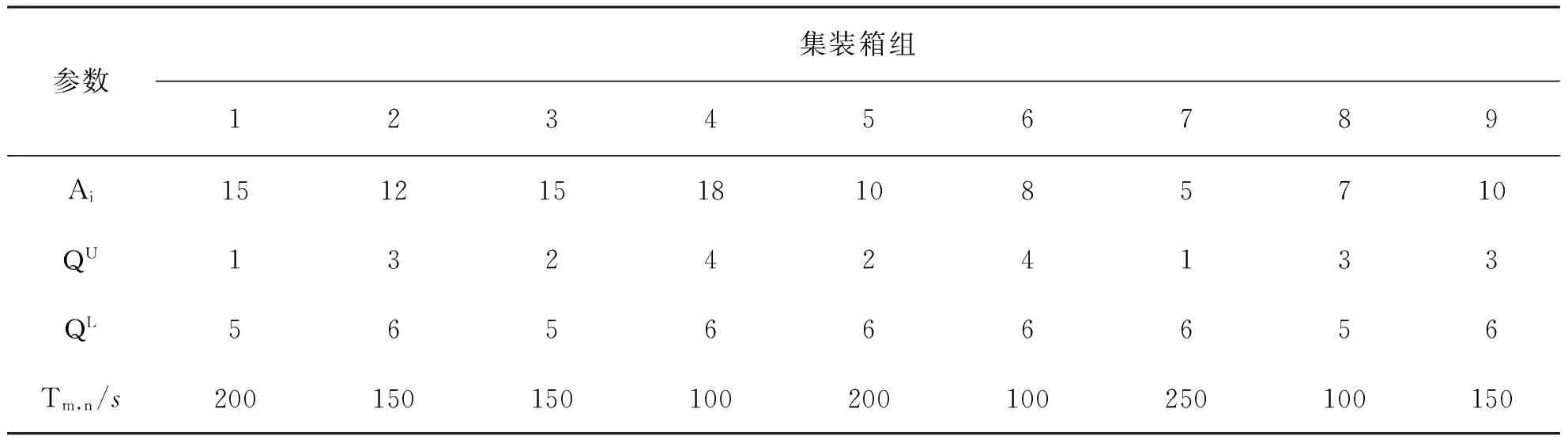
表1　参数值

本文的模型采用CPLEX求解器对模型进行求解。采用的计算机配置是P4 2.4GHz处理器和2GB内存。求得实例中集装箱组从一程船上开始卸下的时间以及集装箱组开始装载的时间如表2所示，表中的数据表明[M1]中的集装箱装卸时间和[M2]中的装卸时间除了第二个集装箱相同之外，其他的都不同。在此时，在[M1]和[M2]模型中完成时间分别为5 730s、5 790s，岸桥的等待时间分别为9 240s、1 310s。虽在[M1]中的完工时间比[M2]中的完工时间减少了60s，但[M2]中岸桥的等待时间比[M1]中岸桥的等待减少了7 930s。

为了更加清楚地了解每个集装箱组的作业调度安排，根据表2中的结果得出图3、4。从图3(a)和图3(b)可以看出[M1]和[M2]中每个集装箱开始作业及作业结束的时间。从图4(a)和图4(b)可以看出模型中岸桥对集装箱的作业顺序。[M1]中1～6岸桥的作业线路分别为：1→7、3→5、2→9→8、4→6、1→3→8、2→4→9→6→5→7。根据图5得出[M2]中1～6岸桥的作业线路分别为：1→7、3→5、2→9→8、4→6、1→8→3，2→9→7→4→6→5。通过将岸桥的线路进行对比发现在两个模型中卸载岸桥对集装箱的作业顺序都是相同的，装载岸桥的作业顺序都不同。说明在集装箱组数为9，且中转完工时间最小时，岸桥的等待时间不是最小的。所以，在追求完工时间最小的目标前提下，同时考虑岸桥的等待时间可以使结果更优，即[M2]的求解效果。

表2　实验结果

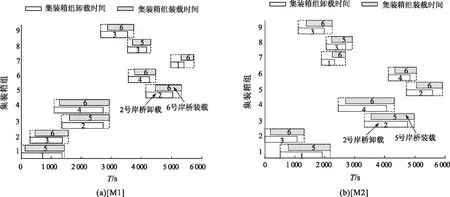
图3　集装箱组开始装卸的时间Fig.3　The time of container groups starting the loading and unloading

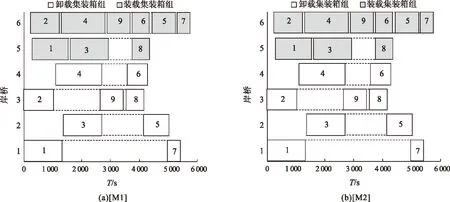
图4　岸桥装卸集装箱组顺序Fig.4　Container handling sequence

为了分析集装箱组数对完工时间的影响，将集装箱组数分别设置为5、7、9、11、13、15、17，求得[M1]和[M2]的结果如表3所示。根据集装箱组数和中转完工时间可以得出集装箱组数和完工时间之间的变化趋势图，具体如图5所示。同时鉴于权重值对中转完工时间和岸桥等待时间的影响，设置了多组权重值，求得结果如图6所示。

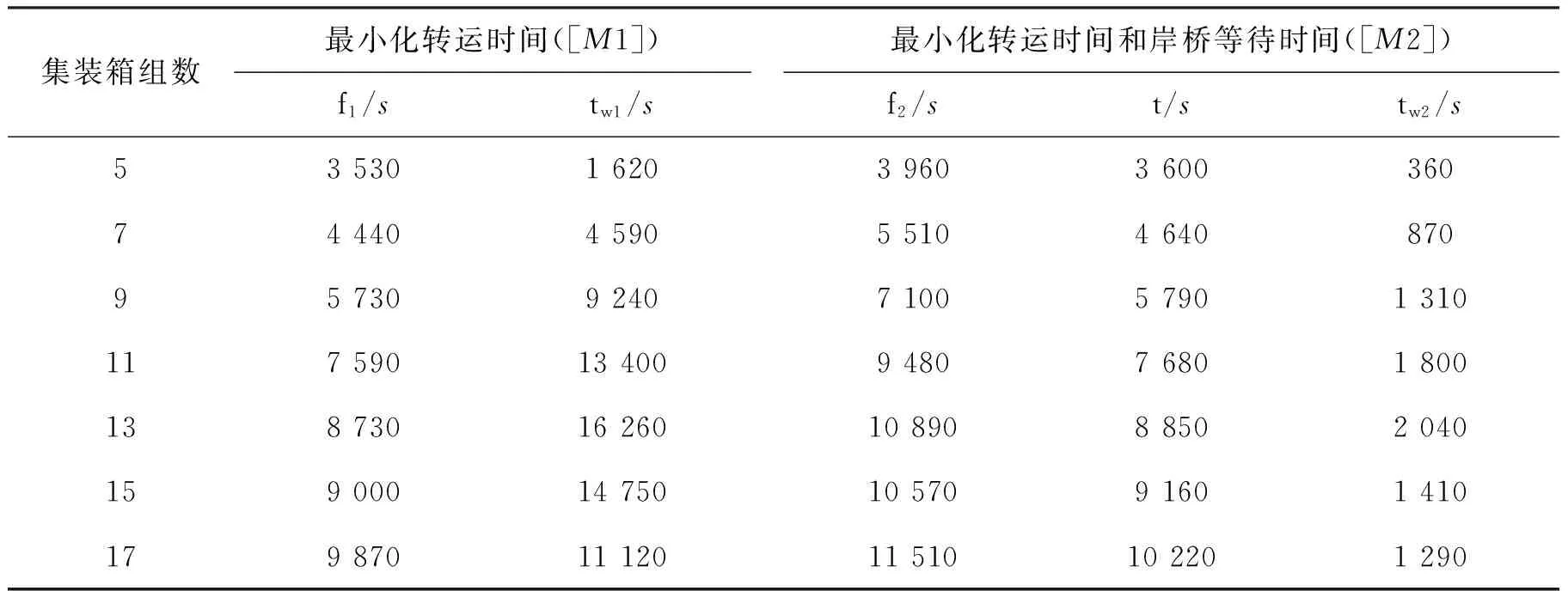
表3　模型求解结果

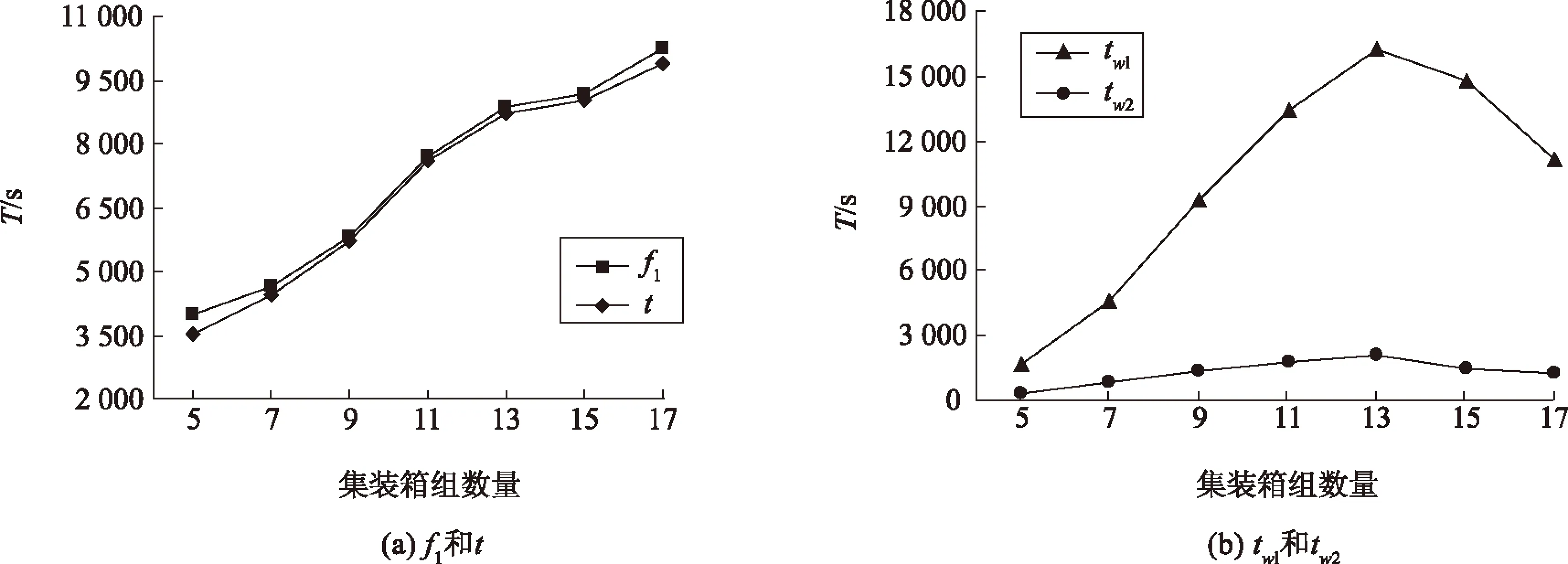
图5　集装箱组数实验结果的影响Fig.5　The influence of the number of container groups on the experimental results

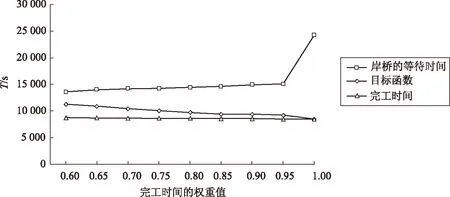
图6　完工时间权重对结果的影响Fig.6　The effect of weight on the result of completion time

从图5中可以看出，随着集装箱组数量的增加，[M1]和[M2]求得中转完工时间逐步上升，[M1]中的完工时间始终是大于[M2]中完工时间，但差值较小；同时，可以看出集装箱组数量对[M1]中岸桥的等待时间的影响很大，对[M2]中岸桥的等待时间影响相对来说很小，随着集装箱组数量的增加，[M1]和[M2]中岸桥的等待时间均呈现先增后减的趋势，[M1]中岸桥的等待时间远远大于[M2]中岸桥的等待时间。

从图6可以看出，当只考虑中转完工时间时，中转完工时间最小，岸桥的等待时间最大；当同时考虑中转完工时间和岸桥的等待时间时，随着中转完工时间权重的增加，岸桥等待时间、目标函数值均呈下降的趋势，而完工时间呈上升的趋势，但上升的趋势很缓慢。

4结论

本文研究了自动化集装箱码头成组直接中转的岸桥作业调度问题，即集装箱以成组和直接中转的方式从一程船上卸载到二程船上，并从单目标优化和多目标优化的角度，分别建立了不同的优化模型。针对每个模型分别设计了7组算例，并分析了集装箱组数、完工时间、岸桥等待时间三者之间的关系。

计算结果表明在集装箱总数相同的情况下，当只考虑将中转完工时间最小化时，在一定范围内，随着集装箱组数的增加，中转完成时间会逐渐增加；当同时考虑中转完工时间和岸桥等待时间最小时，在一定范围内随着组数的增加，完工时间也随着增加，并始终微小于只考虑中转时间最小情况下求得的完工时间，而岸桥的等待时间远远小于前者。岸桥的等待时间和中转完工时间之间博弈的利益均衡点应该根据不同集装箱码头岸桥的特点与船靠泊时间的要求作出考量，其利益均衡点应该在实际操作中把握。

分析自动化集装箱中转码头在成组和直接中转方式下时中转完工时间、岸桥等待时间、集装箱组数之间的关系，对提高中转的效率具有重大的意义。由于本文只考虑岸桥在中转过程中的作业调度，没有将AGV的作业调度考虑进来，并且所做的研究是针对较小规模的中转作业调度问题。而现实自动化集装箱码头成组直接中转的岸桥作业调度更为复杂，本文今后有待拓展的地方包括：研究大规模的自动化集装箱码头成组直接中转的岸桥作业调度问题；研究AGV在自动化集装箱码头成组直接中转过程中的路径问题；研究并设计更加高效、快速的求解算法。

参考文献：

[1]匡海波， 牛文元. 集装箱港口多期投资优化决策模型研究[J]. 管理科学学报， 2012， 15(5)：76-82.

[2]董岗， 朱道立. 港口集疏运通道投资与多车型拥挤收费均衡[J]. 管理科学学报， 2013， 16(5)：83-94.

[3]WUYue，LUOJiabin，ZHANGDali，etal.Anintegratedprogrammingmodelforstoragemanagementandvehicleschedulingatcontainerterminals[J].ResearchinTransportationEconomics， 2013，42(1)：13-27.DOI：10.1016/j.retrec.2012.11.010.

[4]FUYimin，DIABATA，TSAIIT.Amulti-vesselquaycraneassignmentandschedulingproblem：Formulationandheuristicsolutionapproach[J].ExpertSystemswithApplications， 2014， 41(15)：6959-6965.DOI:10.1016/j.eswa.2014.05.002.

[5]TIERNEYK，PACINOD，JENSENRM.Onthecomplexityofcontainerstowageplanningproblems[J].DiscreteAppliedMathematics， 2014， 169：225-230.DOI:10.1016/j.dam.2014.01.005.

[6]CARLOHJ，VISIFA，ROODBERGENKJ.Storageyardoperationsincontainerterminals：Literatureoverview，trends，andresearchdirections[J].EuropeanJournalofOperationalResearch， 2014， 235(2)：412-430.DOI:10.1016/j.ejor.2013.10.054.

[7]毛钧，李娜，靳志宏.基于混堆模式的集装箱码头堆场空间资源配置优化[J]. 大连海事大学学报， 2014,40(1)：117-122.DOI:10.16411/j.cnki.issn1006-7736.2014.01.017.

[8]魏航.集装箱码头堆场取箱时间窗优化研究[J].管理科学学报，2011，14(9)：21-36.

[9]孙凯.关于集装箱码头前沿操作工艺应对船舶大型化的研究[J]. 中国远洋航务， 2015(1)：60-62.

[10]林浩，唐勤华.新型集装箱自动化码头装卸工艺方案探讨[J]. 水运工程， 2011(1)：158-163.DOI:10.16233/j.cnki.issn1002-4972.2011.01.004.

[11]郑见粹，李海波，谢文宁，等. 自动化集装箱码头装卸工艺系统比较研究[J].水运科学研究， 2011(2)：26-33.

[12]邢曦文， 毛钧， 张睿，等. 基于混合流水作业组织的集装箱码头装卸作业集成调度优化[J]. 中国管理科学， 2014， 22(10)：97-105.

[13]范志强， 乐美龙. 最小化最大完工时间与等待时间的岸桥作业调度双目标优化及其遗传算法[J]. 系统管理学报， 2013， 22(1)：120-127.

[14]ZHANGHaipeng，KIMKH.Maximizingthenumberofdual-cycleoperationsofquaycranesincontainerterminals[J].Computers&IndustrialEngineering， 2009， 56(3)：979-992.DOI:10.1016/j.cie.2008.09.008.

[15]DIABATA，THEODOROUE.Anintegratedquaycraneassignmentandschedulingproblem[J].Computers&IndustrialEngineering， 2014， 73：115-123.DOI:10.1016/j.cie.2013.12.012.

[16]FUYimin，DIABATA.Alagrangianrelaxationapproachforsolvingtheintegratedquaycraneassignmentandschedulingproblem[J].AppliedMathematicalModelling， 2015， 39(3/4)：1194-1201.DOI:10.1016/j.apm.2014.07.006.

[17]NGUYENS，ZHANGMengjie，JOHNSTONM，etal.Hybridevolutionarycomputationmethodsforquaycraneschedulingproblems[J].Computers&OperationsResearch， 2013， 40(8)：2083-2093.DOI:10.1016/j.cor.2013.03.007.

[18]EXPSITO-IZQUIERDOC，GONZLEZ-VELARDEJL，MELIN-BATISTAB，etal.Hybridestimationofdistributionalgorithmforthequaycraneschedulingproblem[J].AppliedSoftComputing， 2013， 13(10)：4063-4076.DOI:10.1016/j.asoc.2013.05.006.

[19]KAVESHGARN，HUYNHN，RAHIMIANSK.Anefficientgeneticalgorithmforsolvingthequaycraneschedulingproblem[J].ExpertSystemswithApplications， 2012， 39(18)：13108-13117.DOI:10.1016/j.eswa.2012.05.091.

[20]HOMAYOUNISM，TANGSH，MOTLAGHO，Ageneticalgorithmforoptimizationofintegratedschedulingofcranes，vehicles，andstorageplatformsatautomatedcontainerterminals[J].JournalofComputationalandAppliedMathematics， 2014， 270：545-556.DOI:10.1016/j.cam.2013.11.021.

[21]CHENJianghang，LEEDH，GOHM.Aneffectivemathematicalformulationfortheunidirectionalcluster-basedquaycraneschedulingproblem[J].EuropeanJournalofOperationalResearch， 2014， 232(1)：198-208.DOI:10.1016/j.ejor.2013.06.051.

(责任编辑黄勇)

doi:10.16088/j.issn.1001-6600.2016.02.012

收稿日期：2015-11-22

基金项目：国家自然科学基金面上项目(71471109)；国家自然科学基金青年项目(71101088)；教育部博士点基金项目(20113121120002)；交通部应用基础研究项目(2015329810260)；上海市教委科研创新项目(14YZ100)；上海市曙光计划项目(13SG48)

中图分类号：U693.35

文献标志码：A

文章编号：1001-6600(2016)02-0081-09

AQuayCraneSchedulingofGroup-basedStrategyandDirectTransshipmentatAutomatedContainerTerminal

ZHOUXiudan，HUZhihua，WEIChen

(LogisticsResearchCenter，ShanghaiMaritimeUniversity，Shanghai201306，China)

Abstract:Aiming at the quay crane scheduling problem of group-based strategy and direct transshipment at automated container terminal, this paper studies the relationship of the completion time of transfer process, the waiting time of quay cranes and the number of container blocks is studied in this paper. First of all, an optimization model is established to minimize the makespan. Then, based on this model, a multi-objective model is established to minimize the makespan and the waiting time of quay crane. Through numerical examples, in the case of different container groups, the completion time and the starting time of the container group are obtained, and the influence of the number of containers on the time of transfer and the waiting time of quay crane is analyzed, which extends the research of quay crane scheduling and provides a reference for the operation of container terminal.

Keywords:automated container terminal； group-based strategy； direct transshipment； quay cranescheduling

通信联系人：胡志华(1977—)，男，湖南宁乡人，上海海事大学教授，博士。E-mail：zhhu@shmtu.edu.cn