基于决策者偏好DE算法的模糊聚类迭代洪灾评估方法

何耀耀，宋晓晨，廖　力

(1.合肥工业大学 管理学院, 合肥　230009; 2.湖北工业大学 电气与电子工程学院, 武汉　430068)



基于决策者偏好DE算法的模糊聚类迭代洪灾评估方法

何耀耀1，宋晓晨1，廖力2

(1.合肥工业大学 管理学院, 合肥230009; 2.湖北工业大学 电气与电子工程学院, 武汉430068)

摘要：权重的选择是各种洪水灾害评估模型中的一个关键而又难以确定的问题。根据现有主观赋权法和客观赋权法的特点，在差分进化(DE)算法的基础上，引入决策者偏好过滤掉不满足条件的个体，通过优化考虑决策者偏好的模糊聚类迭代模型获得洪灾样本的指标权重向量，结合洪灾损失样本特征值矩阵得出各样本的灾情综合评价值；然后依据灾情综合评价值与聚类矩阵求出各等级的特征值，并依此自动识别聚类矩阵中各行的类别属性；最后依据识别出的类别属性和各样本的灾情综合评价值，对洪灾样本在不同的决策者偏好下进行等级划分和灾情排序。以2013年四川省和1996年新疆的洪灾样本为例进行仿真试验，实现了不同决策者偏好下的洪灾等级评估，并为水利部门选择偏好类型提供了参考性建议。

关键词：洪水灾害评估；决策者偏好；DE算法；模糊聚类迭代模型；灾情综合评价值

洪水灾害给社会带来巨大的经济损失和人员伤亡,准确及时地对洪灾等级进行估定，可以为洪泛区政府及时制定救灾援灾方案提供依据。确定合理的指标权重是准确评估洪灾等级的基础也是洪灾评估模型中一个关键的问题。对各指标权重的设定直观地体现了决策者对某项指标的偏重程度。目前，洪灾等级评估中指标权重的确定方法可以分为3类，即主观赋权法、客观赋权法和综合赋权法。主观赋权法依据决策者的经验判断对各灾情指标赋权，属性的相对重要程度一般不会违反人们的常识，但其随意性较大，评估结果缺乏准确性和可靠性。如：层次分析法[1]、模糊聚类[2]等；客观赋权法根据灾情数据特征利用一定的数学模型，通过计算得出属性的权重系数,存在客观的赋权标准，其缺点是忽视了决策者的主观认知与经验等主观偏好信息，可能会出现权重系数与主观认知偏差较大的现象，从而使得评估结果不合理。如：投影寻踪[3]，支持向量机[4]等；综合赋权法[5-7]是对各种评估结果的权值进行重新分配，虽同时考虑了主客观因素，但其主观体现在对于各模型评估结果的处理上，增加了模型复杂度，且评估结果对基础模型的选取依赖性较大。为了在降低算法复杂度的同时使评估结果在符合人们认知的基础上尽量科学化，本文提出了一种基于决策者偏好差分进化(DE)算法的模糊聚类迭代评估方法。

1考虑决策者偏好的洪灾评估模型构建

目前，考虑决策者偏好的研究方法并不多见，大多集中在多属性决策问题中。本文在客观权重的基础上加入决策者的主观意识，把决策者偏好的约束加入到DE算法里面，将人的主观意识定量化，结合模糊聚类迭代模型求得决策者偏好下的客观最优权重，在每次迭代的过程中直接过滤掉不满足约束的个体，提高了算法的效率，最后在等级值的计算中运用决策者偏好的处理结果，使得洪灾等级评估结果在科学的基础上充分体现人性化。

1.1模糊聚类迭代模型

洪水灾害的灾情等级评估中，所涉及到的指标比较多，各指标数据间存在冲突明显、非线性、强耦合、不确定等复杂特性，等级评估结果应综合考虑受灾人口、受损房屋、受灾面积和直接经济损失等多个灾情指标，同时因洪灾等级的评估没有确定的指标标准，为此，这里以陈守煜教授创立的工程模糊集理论[7]为基础，引用模糊聚类迭代(FCI)模型实现洪水样本的自然分类。

其目标函数为

(1)

式中：uhj为洪灾样本j相对于洪灾类别h的相对隶属度；sih为第h个类别对第i个指标的相对隶属度；wi为第i个指标的权重；n为洪灾样本个数；c为洪灾类别个数。即：洪水样本集对于全体类别加权广义欧式权距离的平方和最小，式中rij是根据模糊集优化理论，对各样本指标值xij进行归一化处理的结果，以消除各指标间物理量量纲的影响。归一化公式为

(2)

根据拉格朗日函数法，可求得模糊聚类矩阵U和模糊聚类中心矩阵S中的各个元素。

(3)

式中：sik为第k个类别对第i个指标的相对隶属度；m为指标个数。

为满足各指标权重和为1的约束，本文引用文献[6]中所采取的罚函数法，采用式(4)处理约束条件式：

(4)

式中M为罚函数的惩罚系数，这里设定M=106。

1.2考虑决策者偏好的DE算法

本文在用DE算法进行客观赋权时引入一个符合决策者偏好的过滤项，提出了一种基于决策者偏好模糊聚类迭代模型的综合赋权法，该方法兼顾决策者对属性的偏好使得评估结果更加符合人们的认知，同时又力争减少赋权的主观随意性，使对属性的赋权达到主观与客观的统一。

以下针对本文的研究内容对加入了决策者偏好的DE算法的运行加以介绍。

步骤1，初始化种群：设置初始进化代数t=0，随机生成种群。

(5)

式中：qij为第i个个体的第j个分量；rand为(0,1)间的随机数；qmax,j，qmin,j分别为第i个个体的第j个分量的上、下界。

步骤2，变异：DE算法和其他进化算法主要区别是变异操作，也是产生新个体的主要步骤。变异后得到中间个体，即

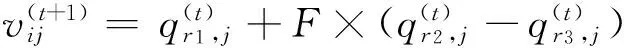
(6)

式中F为变异算子，为(0,1)之间的常数，它控制差分向量的幅度。

(7)

步骤4，过滤：考虑决策者偏好使得所得试验个体中某一特定个体权重最大的才能进入下一步，否则返回到步骤2。

(8)

(9)

实际应用中根据决策者偏好设定过滤约束项。

(10)

步骤6，如果t=Tmax或者满足误差要求，则结束计算；否则t=t+1，返回到步骤2。

步骤7，求各样本的灾情综合评价值C(j)：

“本龙来自糖人国！”休息足够，糖龙的身体也恢复到原来的硬度，它坐起来昂着脑袋，龙须也显得格外飘逸。糖龙因为由糖制成，遇水遇热身体便会融化，一疲劳身体就会变软。不过，这糖龙的性格倒是像龙一样高傲呢。

(11)

Wbest即为决策者偏好下的最优权重向量，R=(rij)为样本特征值矩阵，无偏好时采用等权重的方法。通过程序识别出各洪灾样本的聚类结果在第h行记作mj,将mj=h的所有样本的灾情综合评价值相加记作Mh；然后用Mh除以聚于该行的样本个数Nh，求出模糊聚类矩阵U中每行的等级特征值Bh，通过等级特征值最终确定U中各行所代表的洪灾等级，以及各样本的灾级属性，最后在各灾级内利用式(11)所得的灾情综合评价值进行排序。

1.3算法流程图

本文首先在DE算法的基础上加入了过滤项，使得只有满足决策者偏好约束的个体才能进入程序，其次在算法末尾加入灾情综合评价值和等级特征值指标，实现了各样本类别属性的自动识别以及对各灾情等级内部样本按其灾情大小进行排序的功能。帮助管理人员有针对性地进行救灾援灾决策。考虑决策者偏好的DE算法流程如图1所示。

图1　考虑决策者偏好的DE算法流程

2仿真试验

为充分说明决策者偏好的作用，本文选择2组不同特点的洪灾损失数据进行评估，采用的DE算法参数如下：种群规模为50，变异算子为0.7，交叉算子为0.9，迭代次数为100，ε1和ε2均为10-4，模糊聚类迭代模型循环迭代10次。

2.1案例1

决策者偏好在模型中体现在评估时某一项或多项指标的权重更大，下面对2013年四川省部分地区洪灾样本(表1，样本排序以洪灾初始发生时间为准)在不同决策者偏好约束下进行比较评估。在4种不同的偏好信息下(①无偏好；②偏好1：受灾人口权重最大；③偏好2：直接经济损失权重最大；④偏好3：受灾人口权重最大,直接经济损失其次)进行模糊聚类分析，得出聚类结果。不同决策者偏好下的权重见表2，洪灾等级结果见表3。

表1　2013年四川省部分地区洪灾损失样本Table 1　Samples of flood loss in Sichuan in 2013

表2　案例1中不同决策者偏好下的权重Table 2　Weight vectors in the presence of different preferences of decision-maker in scheme 1

据中华人民共和国民政部救灾司相关报道，对于6月29日起部分地区发生的洪灾(即样本5)，四川省减灾委、民政厅于7月1日9时，启动三级救灾应急响应。7月7日起四川省部分地区发生的洪灾(即样本8)，国家减灾委、民政部于7月11日，指导四川暴雨洪涝灾害三级救灾应急响应工作组在汶川县和都江堰市开展救灾工作，样本8灾情损失数据是7月7日起发生的洪灾在7月15日统计出的结果。由于统计时间晚于救灾工作，灾情时间持续较长，该数据的各指标又全部偏大，因此，评估结果定为Ⅳ类还是比较可靠的，对于其他地区的灾级评价结果，可供参考。

表3　案例1洪灾等级评估结果Table 3　Results of flood rating in scheme 1

由表2可以看出，在不同的偏好约束下，得出的权重有明显的差别。分析灾情等级评估结果，表3中Ⅳ类洪灾样本1个，Ⅲ类1个，Ⅱ类4个，而Ⅰ类却高达12个，远远超过洪水样本总数的50%，而结合灾情具体指标数据可知，在1类样本中的很多数据的差别还是很大的。本文对各样本的类别特征值进行排序，看出样本12和3同属于Ⅰ类洪水，但在不同的决策者偏好下其相对灾情的大小还是有差别的。当决策者以经济损失为考虑重点时，样本12的洪水灾情相对会重些，而决策者以受灾人口为重点考虑时，样本3的洪水灾情却比样本12重。因此，决策者在根据灾情等级实施救灾援灾策略时也应有轻重之别，不能说同一等级下的洪灾都采取同样的决策。

这里选取的是2013年间四川省的部分区域发生的18个洪灾样本，地区间经济情况人口密度差异性不大，因此，在计算样本灾情综合评价值时无论对样本特征值矩阵是否乘权重，对于评估及排序结果都没有什么影响。但并不是对所有的样本计算灾情综合评价值所采取的方式不同，评估结果都是一样的。

2.2案例2

在计算等级特征值时对样本特征值矩阵是否乘权重，对于评估结果是存在很大的影响的。本文选取新疆1996年7月部分地区的洪灾损失(表4)样本[5]进行分析，该案例样本数据各指标间差别较为明显。分析得出不同决策者偏好下的权重见表5，洪灾等级评估结果见表6。

无偏好时为使得评估结果尽量客观化，在灾情综合评价值的计算过程中，使样本特征值矩阵中各指标权重一致，从而削弱权重对等级评估结果的影响程度。这里的分类结果与文献[5]中一致。 而当存在决策者偏好时，我们这里考虑在灾情综合评价值的计算过程中，对样本的特征值矩阵乘上算法中最能体现决策者偏好的结果——指标权重向量，从而使得决策者偏好的思想不仅仅是在程序中起到过滤的作用，在等级评估与排序中也直接体现决策者偏好。

表4　新疆1996年7月部分地区洪灾损失Table 4　Samples of flood loss in Xinjiang in July 1996

表5　案例2中不同决策者偏好下的权重Table 5　Weight vectors in the presence of different preferences of decision-maker in scheme 2

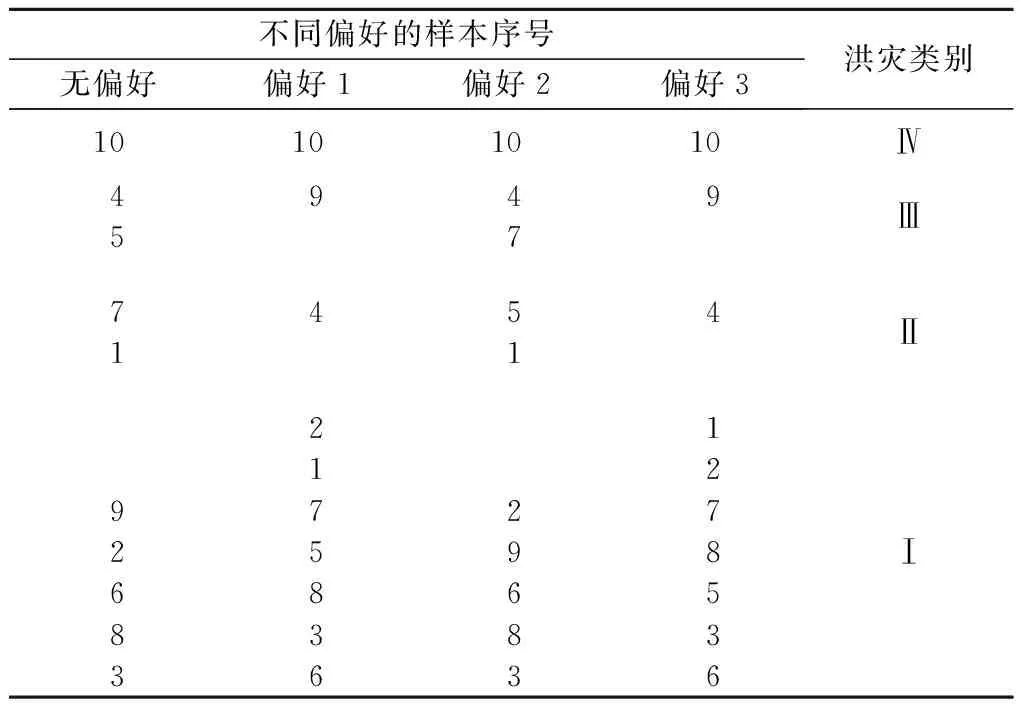
表6　案例2洪灾等级评估结果Table 6　Results of flood rating in scheme 2

综合表5和表6分析：无偏好时受损房屋项权重最大为0.873 8，这使得等级评估结果偏向于依据房屋损坏量进行聚类。这里分析2个特殊的样本说明分类的不合理性：样本5在无偏好下的等级评估结果是Ⅲ类洪灾，但事实上样本5就是房屋损坏数量较大，其他灾情指标并不严重，如果相关部门是依照这个结果采取相应的救灾援灾方案就会造成救灾物资的浪费，也不一定能达到理想中的效果；样本9在无偏好以及偏好2下的等级评估结果是Ⅰ类洪灾，因为房屋损坏量和直接经济损失较小，但结合具体的损失数据可以发现，样本9的受灾人口高达20万人在该组样本受灾人口中居于第二，所以在决策者偏好1和3中它被归为了Ⅲ类洪灾，如果相关部门是依照无偏好和偏好3下的评估结果来给予相应的救助，救灾力度显然不够，受灾人口过多而没有得到相应的救助，不利于社会的稳定和洪泛区的灾后经济复苏。因此，在洪灾等级评估中适当的对相关指标加入权重大小的约束，是使得援灾救灾工作针对性有效进行的依据。

同时，考虑以人为本的观念，只有将受灾人口放在评估的第一位，充分体现相关部门对灾区人民的高度关注，救援方案才能有效地实施，更好地维护洪泛区的社会稳定。同时社会经济的大力发展，使得经济在社会生活中起着越来越重要的作用，将直接经济损失放在第二位，评估工作在考虑人的基础上充分重视洪灾对地区经济的影响，实施相应的救援措施，有利于洪泛区灾后经济复苏。因此，实际评估工作中，本文建议采取偏好3。本文列出其他偏好情况是为了做个比较，说明决策者偏好的意义。

3结论

在模型算法方面：本文在DE算法的基础上加入了决策者偏好信息作为算法优化权重过程中的过滤项，将决策者的主观因素定量化，结合FCI模型不断更新适应值，使得最终的算法运行结果中模糊聚类矩阵和最优权重向量中都含有决策者偏好的信息，然后利用这个结果求得各样本的灾情综合评价值进行灾情排序和等级评定。案例结果表明：模型评估结果是可靠的，并且在进行洪灾等级评估时，加入决策者偏好信息，能使洪灾等级评估的结果会更有实际意义。

案例分析方面：在案例1中，我们选取四川省部分地区洪灾样本，地区间人口集中度、经济水平差距不大，指标间数据冲突不明显，评估结果中不同决策者偏好下各样本等级划分结果类似，只是同一等级下样本灾情排序结果不同；案例2中，洪灾样本地区间人口集中度、经济水平等差距较大，会出现指标间数据冲突明显的状况。针对这种案例2，本文给出了一个较为有效的处理方案：无偏好时灾情综合评价值的计算就是样本特征值矩阵中各灾情指标直接相加再除以聚类结果处于同一类的样本个数，而当存在决策者偏好时就要先对样本特征值矩阵乘上最优权重向量再处理。这样的处理方式，能够保证在客观条件下得出无偏好聚类结果，而在考虑决策者偏好时，可以更好利用最优权重，使得等级评估结果在科学化的基础上更加符合经验判断。

参考文献：

[1]詹小国, 祝国瑞, 文余源. 综合评价山洪灾害风险的 GIS 方法[J]. 长江科学院院报,2003,20(6): 48-50.

[2]廖力，周雪芹，邹强,等. 基于模糊聚类迭代模型的洪灾评估标准计算方法[J]. 长江科学院院报, 2015, 32(2):34-38.

[3]陈曜,丁晶, 赵永红. 基于投影寻踪原理的四川省洪灾评估[J]. 水利学报, 2010, 41(2):220-225.

[4]杨阳,方春晖,李占超,等. 基于最大熵的坝体健康评估专家模糊赋权模型[J]. 长江科学院院报，2011,28(3):20-23.

[5]HE Y Y, ZHOU J Z, KOU P G,etal. A Fuzzy Clustering Iterative Model Using Chaotic Differential Evolution Algorithm for Evaluating Flood Disaster[J]. Expert Systems with Applications, 2011, 38(8):10060-10065.

[6]LI L, ZHOU J Z , ZOU Q. Weighted Fuzzy Kernel-clustering Algorithm with Adaptive Differential Evolution and Its Application on Flood Classification[J]. Natural Hazards, 2013, 69(1): 279-293.

[7]陈守煜. 工程模糊集理论与应用[M]. 北京:国防工业出版社, 1998:1-221.

(编辑：曾小汉)

收稿日期：2014-12-29； 修回日期：2015-05-14

基金项目：国家自然科学基金项目(71401049)；长江科学院开放研究基金项目 (CKWV2014213/KY, CKWV2014219/KY)

作者简介：何耀耀(1982-)，男，安徽宣城人，副教授，硕士生导师，博士，研究方向为水电能源科学，(电话)0551-62919150(电子信箱)hy-342501y@163.com。

doi:10.11988/ckyyb.20141073

中图分类号：X43，TV873

文献标志码：A

文章编号：1001-5485(2016)04-0033-06

A Flood Disaster Evaluation Method Based on Fuzzy Clustering IterationUsing DE Algorithm of Decision-maker’s Preference

HE Yao-yao1, SONG Xiao-chen1, LIAO Li2

(1.School of Management, Hefei University of Technology, Hefei230009, China;2.School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan430068, China)

Abstract:Assigning appropriate weight to different indexes is a key also a difficult problem to various flood disaster evaluation models. According to the characteristics of the present subjective and objective assigning weight methods, decision maker’s preferences is introduced into the differential evolution (DE) algorithm to filter out those individuals which dissatisfy the preferences, and the indexes’ weight vectors of flood samples can be obtained by optimizing the fuzzy clustering iterative model which considers the decision maker’s preferences. Furthermore, with the characteristic value matrix of the floods samples, the comprehensive evaluation value of each flood disaster is obtained. According to the comprehensive evaluation value of each flood disaster and the cluster matrix, the eigenvalue of each degree that is followed by identifying the degree of each row in the cluster matrix automatically, can be obtained. Finally, all the flood samples under different decision maker’s preferences are assessed and sorted based on the identified degree of each row and the comprehensive evaluation value of each flood disaster. Simulation test on two flood samples, namely in Sichuan occurred in 2013 and Xinjiang in 1996, reveals the results of flood rating in different decision maker’s preferences, and provides reference for water conservancy department on choosing preference type.

Key words:flood disaster evaluation; decision maker’s preference; DE algorithm; fuzzy clustering iterative model; comprehensive evaluation value of disaster

2016,33(04):33-38