基于玻璃基底的透明导电金膜的光学性质

彭达球，黄晓江，施芸城

(东华大学 理学院，上海 201620)



基于玻璃基底的透明导电金膜的光学性质

彭达球，黄晓江，施芸城

(东华大学 理学院，上海 201620)

摘要：采用直流溅射法，通过调节溅射时间和溅射电流，在玻璃基底上成功制备出不同厚度的透明导电金膜. 通过椭圆偏振仪测量了透明导电金膜的厚度及其对可见光的透过率，利用四探针、扫描电子显微镜分别测量和表征了透明导电金膜的方块电阻和表面形貌. 研究结果表明，随着透明导电金膜厚度的增加，方块电阻减小，金膜表面连续性变好，且透明导电金膜厚度为10～13 nm时，透明导电金膜的导电性和透过性的兼顾最佳. 通过实际中透明导电金膜厚度随溅射条件的变化，结合理论膜厚计算公式可知，直流溅射沉积透明导电金膜为岛状生长模式. 使用椭圆偏振仪测量了不同入射角度和入射方向上透明导电金薄膜的椭偏参量，发现在各向同性的玻璃基底上生长的透明导电金膜的光学性质表现为各向异性.

关键词：直流溅射； 透明导电金膜； 椭圆偏振仪； 岛状生长模式

透明导电薄膜是一种对可见光(λ=400～760 nm)的平均光透射率高(Tavg>80%)且电阻率低(ρ<10-3Ω·cm)的光电特性薄膜[1]. 自1907年利用镉(Cd)制备出氧化镉(CdO)透明导电薄膜[2]以来，透明导电薄膜的研究备受重视.目前，透明导电薄膜主要包括金属系、氧化物膜系、非氧化化合物膜系、高分子膜系、复合膜系等，其中研究和应用最为广泛的是透明导电金属薄膜和透明导电氧化物薄膜[3-4]. 随着研究的深入，不同类型的透明导电薄膜被研发出来的同时，基底材料也一直是科研人员研究的热点. 由于透明导电薄膜具有优异的透光性，基底材料的光学性质和各向同(异)性会对透明导电薄膜产生何种影响，暂时还没有找到相关文献报道，本文以此为出发点进行研究.

玻璃是一种各向同性的透明介质，能极大程度上发挥透明导电薄膜的透光率优势. 金(Au)具有良好的导电性，并且化学性质稳定，金膜在现代电子行业中应用广泛[5]. 但是前人研究金膜的焦点更多的是关注其电学性质[5-6]，对金膜的光学性质研究甚少.

本文采用直流溅射在玻璃基底上沉积透明导电金膜，通过调节溅射时间以及溅射电流，制备不同厚度的金膜. 利用扫描电子显微镜(SEM)观察金膜的表面形貌，采用四探针测量金膜的方块电阻，并使用椭圆偏振仪测量金膜的厚度以及在不同入射角度和入射方向(以入射光线绕薄膜法线旋转角度标定)上透明导电金膜的光学性质.

1试验部分

1.1沉积材料及仪器

试验所用基底材料为帆船牌CAT.NO. 7105的载玻片，尺寸为25.5 mm×76.2 mm×1.0 mm，靶材采用纯度为99.9%的金. 试验所用镀膜仪为北京中科科仪公司生产的SBC-12型直流溅射仪.

1.2沉积过程

本试验采用直流溅射法沉积金膜，直流溅射仪沉积参数如表1所示.

表1　直流溅射沉积参数

沉积金膜的工艺：(1) 固定溅射时间为80 s，通过控制直流溅射仪的针阀，调节溅射电流为4～8 mA，获得不同厚度的金膜；(2) 固定溅射电流为6 mA， 通过调节溅射时间旋钮控制溅射时间为50～90 s.

1.3试验仪器

采用JSM-5600 LV型SEM观察金膜样品的表面形貌；利用SDY-4型四探针测量金膜的方块电阻；利用SE800E UV-VIS-NIR型光谱椭圆偏振仪测量金膜厚度以及不同入射角度和入射方向上金膜的椭偏参量变化.

2结果与讨论

2.1金膜的导电性及透光率

使用直流溅射法制备金膜时，金膜厚度(d)的计算式[7]为

d=kiVt

(1)

其中：k为一个常数，与直流溅射系统的真空度、靶材与基底间距有关；i为溅射电流；V为固定的直流溅射工作电压；t为溅射时间.

由式(1)可知，当溅射时间恒定时，金膜的理论厚度与溅射电流成正比关系；同样地，当溅射电流恒定时，金膜的理论厚度与溅射时间成正比关系. 利用椭圆偏振仪测量不同溅射时间和溅射电流下的金膜厚度，以及利用四探针测量不同厚度金膜的方块电阻，结果如表2所示.

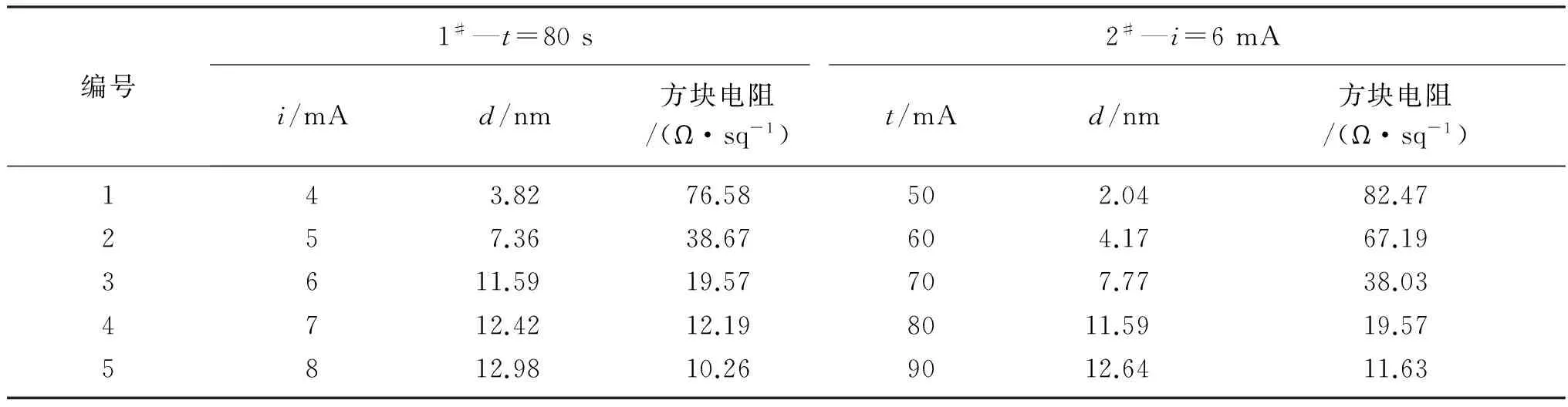
表2　不同溅射电流和溅射时间下的金膜厚度及方块电阻

从表2可以看出，不论是保持溅射时间不变，逐渐增大溅射电流(1#)，还是保持溅射电流不变，逐渐增加溅射时间(2#)，金膜的厚度均随之增加.

使用了SEM分别拍摄不同溅射电流(1#)和不同溅射时间(2#)情况下金膜的SEM照片，结果如图1和2所示.

(a) 1#-1　(b) 1#-2 　(c) 1#-3

(d) 1#-4　(e) 1#-5　

(a) 2#-1　(b) 2#-2　(c) 2#-3

(d) 2#-4　(e) 2#-5　

从图1和2可以看出，随着溅射电流和溅射时间的增加，金膜的表面连续性变好. 结合表2可知，金膜表面连续性越好，其方块电阻越低，则金膜的导电性能越优.

对于金膜而言，因为金原子中自由电子浓度很大，光进入金膜时，会引起金原子内部的自由电子振动，光子在与电子的碰撞中逐渐消耗能量. 如果金膜厚度太厚，能够极大地提高金膜的导电性，但是却严重地牺牲了金膜的透光性；金膜厚度太薄，会使金膜连续性变差而产生断层，从而严重降低金膜的导电性. 为了探究金膜厚度对金膜透射率的影响，从表2中选取5组厚度梯度的金膜，测量其在可见光范围内的透射率，其透射率曲线如图3所示.

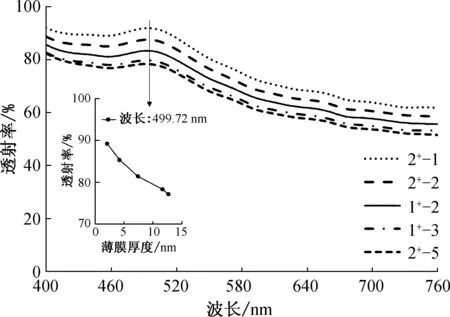
图3　不同厚度金膜的透射率曲线Fig.3　The transmittance curves of gold film ofdifferent thickness

从图3可以看出，在波长为400～500 nm时，透明导电金膜的透射率在75%以上，变化较小；在波长为500 nm左右时，透射率出现一个较小的峰；在波长为500～760 nm时，透明导电金膜的透射率整体呈现减小的趋势. 同时，从图3中还可以看出，随着金膜厚度的增加，其对可见光的透射率呈现减小的趋势.

由固体物理知识[8-9]可知，当光通过薄膜后，透射光强度I的变化为

I=I0·(1-r)2·e-(a+s)d

(2)

其中：I0为入射光强度；r为反射系数；a为吸收系数；s为散射系数.因为金原子的载流子浓度很高，在可见光波段的吸收系数随着波长的增加而增加，透射光强度则随着吸收系数的增加而减小，所以透射率随波长的增加而减小；同时吸收系数与载流子浓度有关，当金膜厚度越厚，载流子浓度增加，透射光强度减小，所以金膜厚度越厚，金膜的透光率越小. 文献[4]研究表明，透明导电金膜的方块电阻为1～102Ω/sq，透光率为60%～80%. 综上可知，金膜厚度为10～13 nm时，金膜的导电性和透光性均非常优良，满足透明导电薄膜的基本特性.

2.2直流溅射的成膜机理讨论

从表2还可以发现，测量的金膜实际厚度与溅射时间、溅射电流的关系并非式(1)理论给出的线性关系. 薄膜厚度增加至12 nm左右时，薄膜生长速度比薄膜厚度小于12 nm时要慢. 造成这种变化趋势的原因可以从金膜的生长机理来讨论，由于金原子和基底之间的浸润性较差，在直流溅射的过程中，金靶中的金原子被激发形成溅射原子，溅射到基底表面时，金原子相互之间的键合力主导薄膜生长，此时的薄膜生长方式称为岛状生长(Volmer-Weber)模式[10]. 在薄膜形成伊始，金原子相互之间的键合力使得薄膜生长速度很快，并且形成一个个小岛，此时垂直于基底表面的薄膜生长速度占据主导地位.而随着小岛的慢慢变大，基底表面的金原子开始扩散迁移，当扩散迁移到一定程度后，与周围相邻的小岛碰撞结合，这样每个小岛之间也慢慢地连接起来而形成连续的薄膜.随着薄膜的进一步生长，平行于基底表面的薄膜生长速度大于垂直方向的薄膜生长速度，薄膜厚度的增加趋势也就开始减缓.

2.3金膜的光学性质

椭圆偏振仪以椭圆偏振光为基础，测量入射光与样品相互作用(包括反射、散射和透射)后光波的偏振态(即椭偏参量Ψ和φ)的变化，通过测量结果计算可以得出薄膜材料的光学性质，具体表达式[11-17]为

tanΨ=|rp|/|rs|

(3)

φ=δp-δs

(4)

其中：tanΨ为反射光的p分量和s分量的振幅系数rp与rs之比；Ψ为偏振角；φ为两偏振分量的相位差；δp和δs分别表示p分量和s分量在反射前后的相位延迟.

由2.1节可知，在溅射电流为6 mA和溅射时间为80 s时，玻璃基底上金膜的透明性和导电性均非常好，因此，本文选择该透明导电金膜样品作为研究对象，研究其在可见光范围内的光学性质. 为探究玻璃基底对金膜光学性质的影响，分别选用未沉积金膜的干净玻璃(GN)和沉积金膜的玻璃(GA)作对比试验. 玻璃是一种透明的基底材料，测量玻璃的椭偏参量时，需要使用小光斑，并且使用小的入射角. 所以，控制椭圆偏振仪机械臂，固定入射角度为50°，测量在可见光范围(400～760 nm)内GN和GA的椭偏参量随波长的变化曲线，如图4所示.

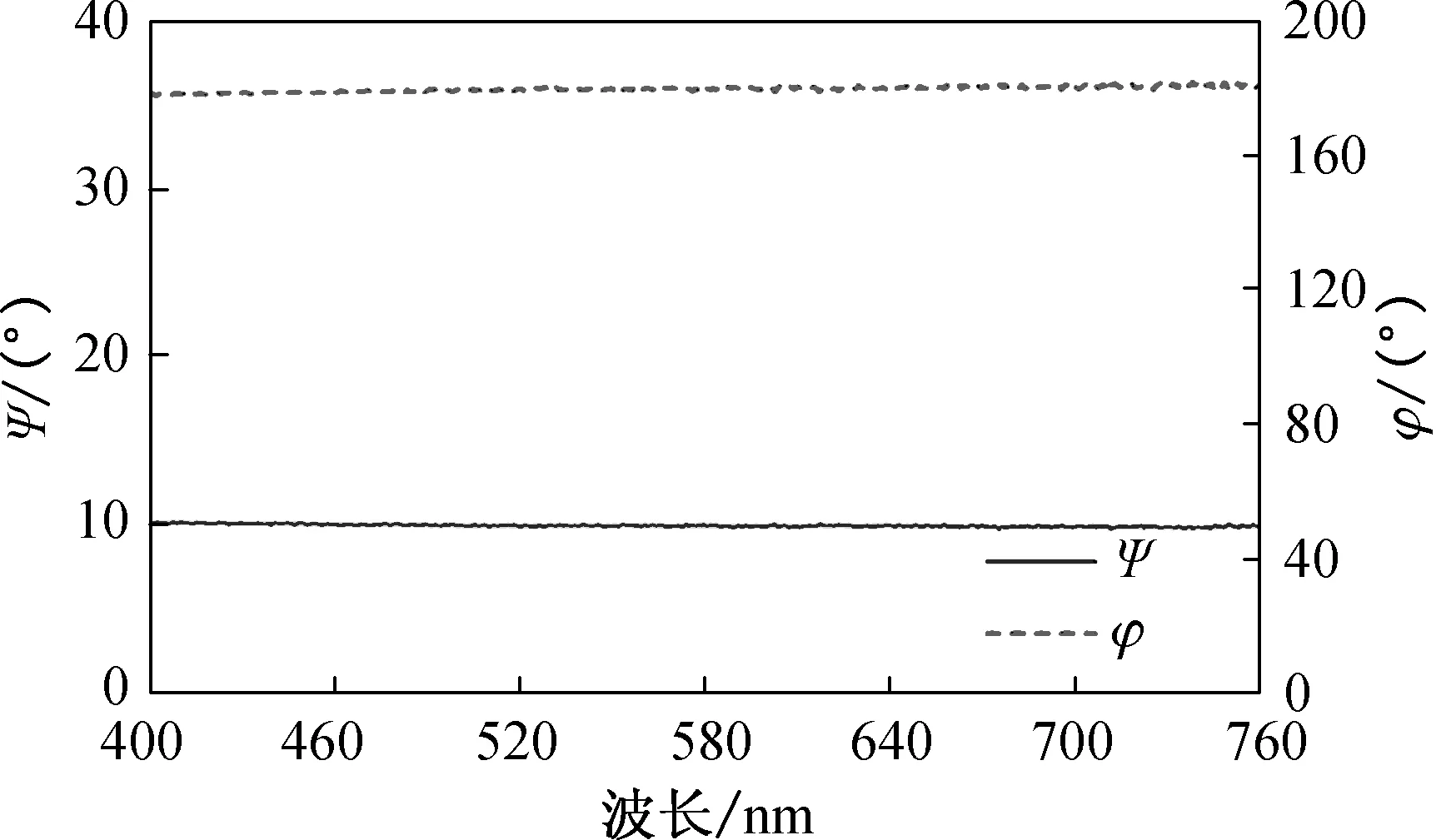
(a) GN

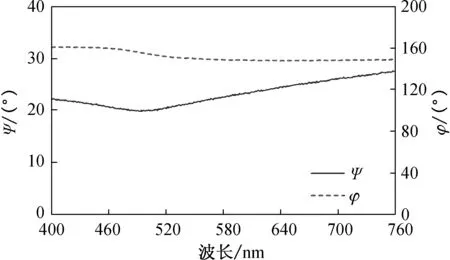
(b) GA

从图4(a)可以看出，在可见光波段内GN的椭偏参量几乎保持恒定值. 因为玻璃是透明基底，不同波长的入射光经过玻璃基底近似镜面反射后，反射光的两个分量的大小不会发生变化，而反射前后的相位差约为180°. 从图4(b)可以看出，GA的Ψ值随波长先减后增，而φ值则是略微减小的. 在玻璃基底上沉积金膜后，因为金膜的成膜方式为岛状生长模式，金膜表面较为粗糙，所以入射光反射后产生一定程度的相位延迟，此时的相位差不再为180°，且金膜对入射光吸收散射后，反射光的两个方向的分量损失不同，所以两个分量的振幅之比也产生相应的变化.

为进一步探究玻璃基底对透明导电金膜的光学性质的影响，首先以步进5°调节椭圆偏振仪的机械臂从50°到70°，获得不同入射角度下GN和GA的椭偏参量随波长的变化曲线. 选取3个波长，分析在这3个波长值下，椭圆偏振仪测量的5个不同入射角度对应的椭偏参量Ψ和φ的变化情况，如图5所示.

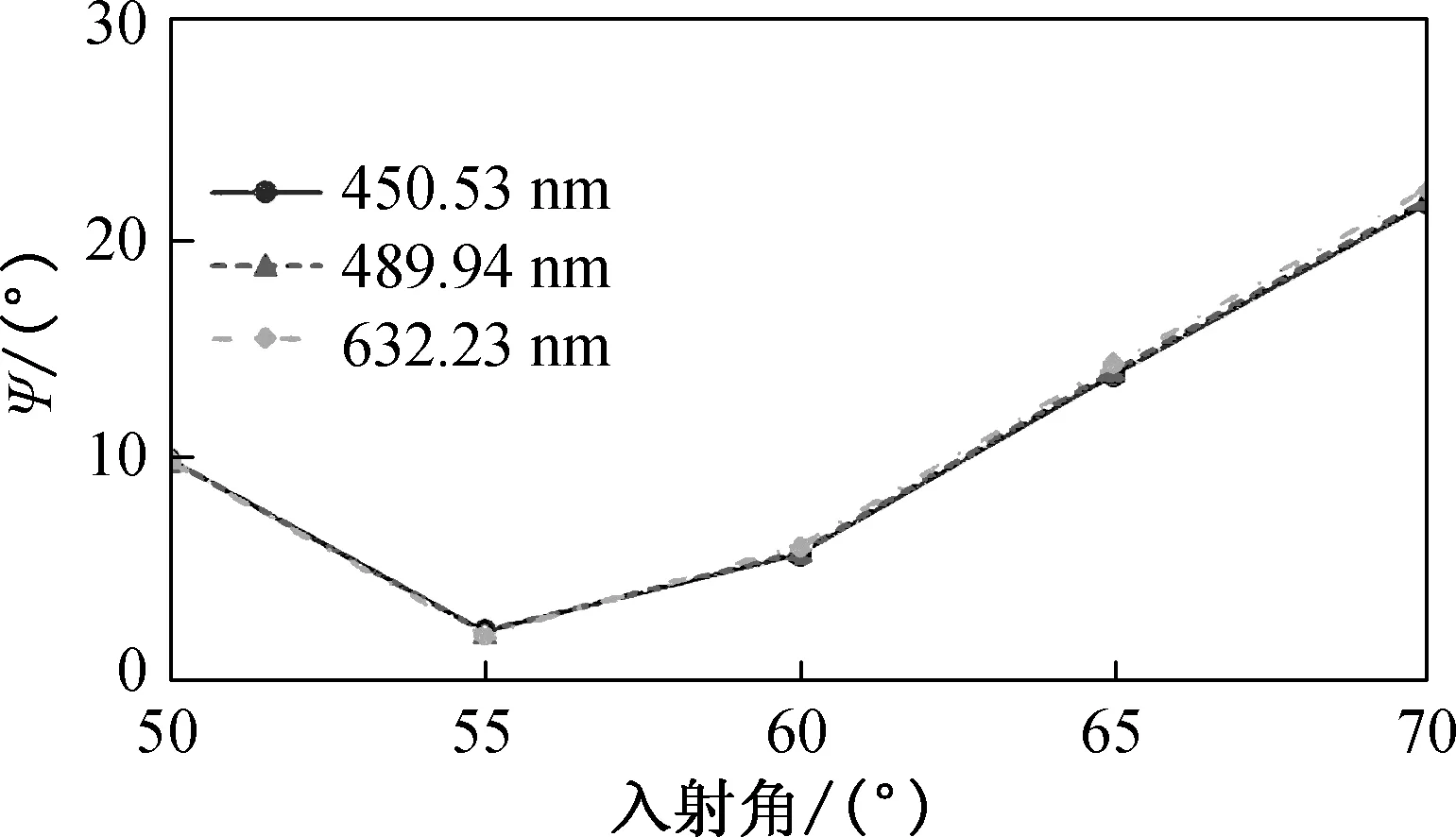
(a) GN的椭偏参量Ψ

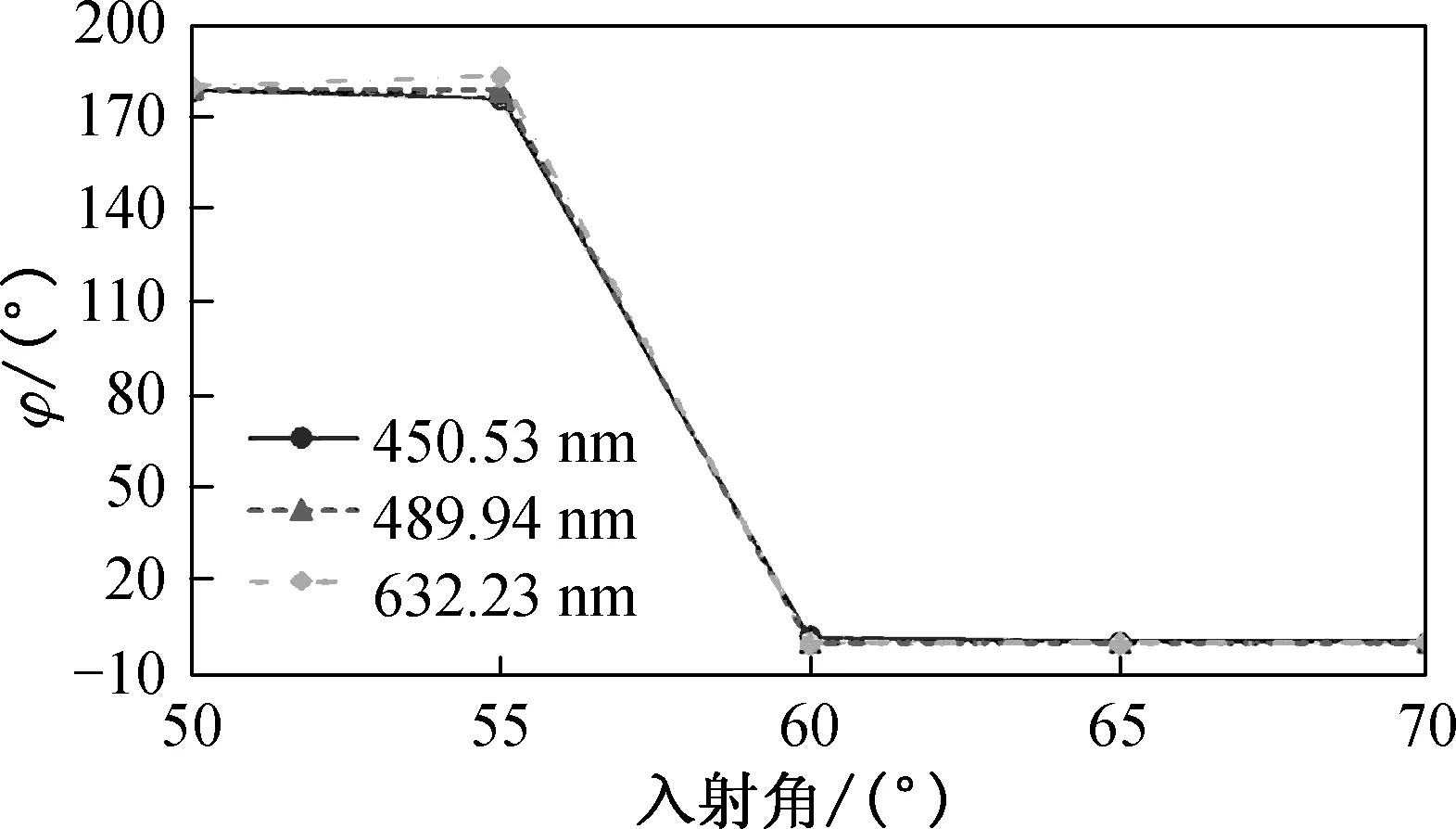
(b) GN的椭偏参量φ

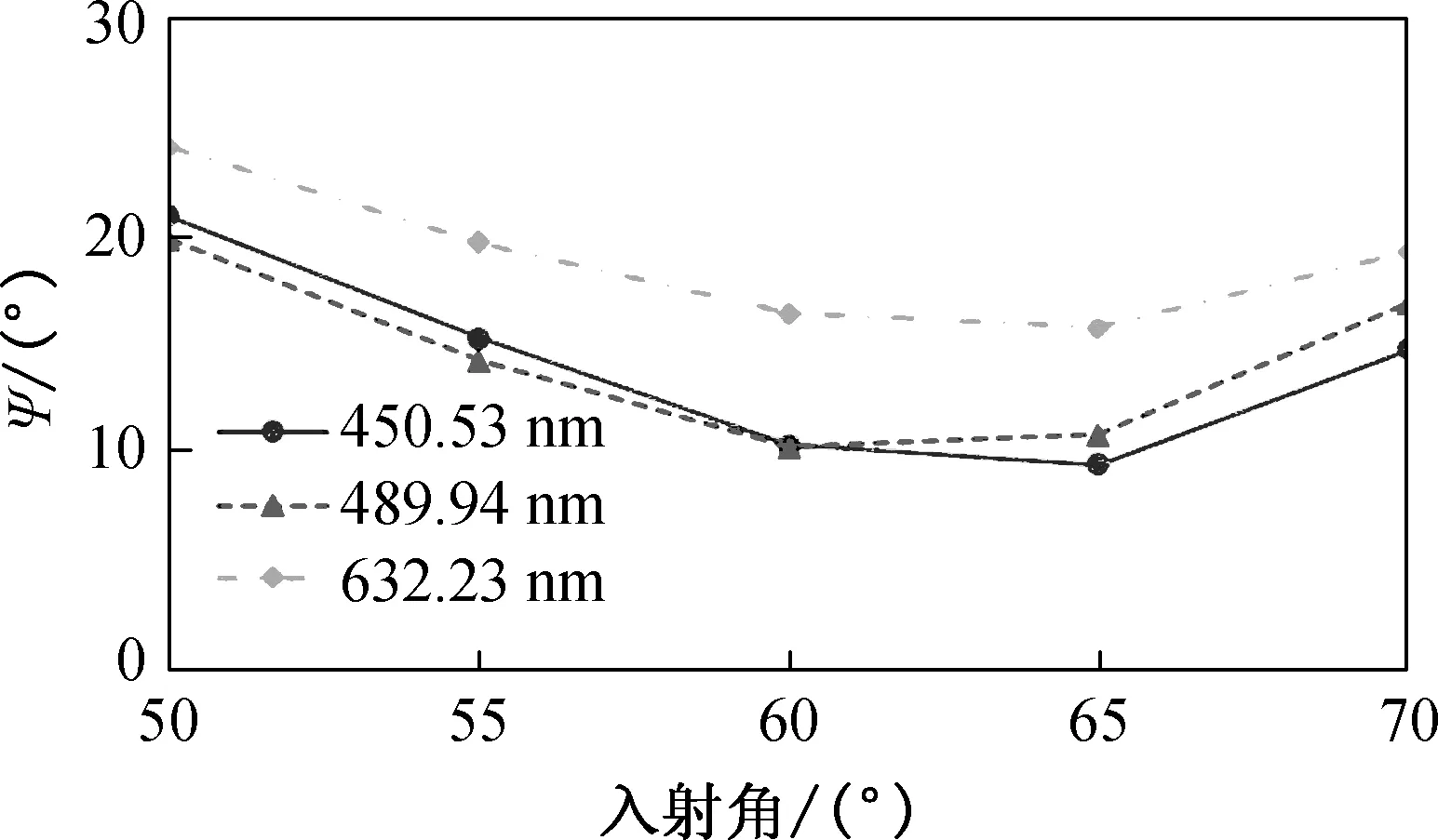
(c) GA的椭偏参量Ψ

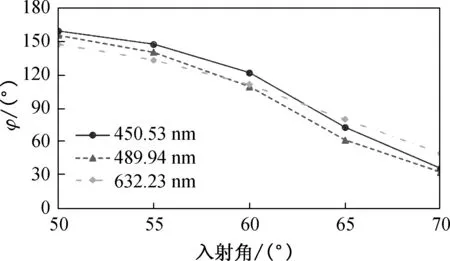
(d) GA的椭偏参量φ

从图5(a)和5(b)可以看出，在不同的波长值时，GN的椭偏参量没有太大变化.但是GN的椭偏参量Ψ随着入射角度的增加，大体呈上升趋势；入射角度为50°和55°时，GN的椭偏参量φ约为180°，而入射角度为60°～70°时，GN的椭偏参量φ约为0°. 因为玻璃虽然是各向同性基底，但是玻璃基底表面并不光滑，随着入射角度变化，入射光的偏振性相应地改变，相位则产生相应的延迟或提前，所以会产生相位差0°和180°的较为规则的变化. 从图5(c)和5(d)中可看出，GA的椭偏参量均大体呈下降趋势. 在玻璃上沉积金膜后，因为金膜表面的粗糙引起的反射光损耗，使得反射光的两个方向的分量损耗程度不同， 而且随着入射角度变化，入射光通过金膜的光程随之变化，使得反射光与入射光的相位差也发生了变化.

其次，固定椭圆偏振仪的机械臂的角度为50°，即入射角度为50°，旋转样品，规定样品长边为0°，每次旋转增加30°，旋转一圈，测量并记录这12个旋转角度下的样品的椭偏参量随波长的变化曲线. 同样地选取3个波长，分析不同入射方向上GN和GA的椭偏参量的变化，如图6所示.

从图6(a)和6(b)可以看出，随着玻璃基底的旋转，在各个入射方向上GN的椭偏参量的变化很小. 因为玻璃是一种各向同性的介质，在各个方向上的光学性质相同，图中的微小变化是因为玻璃表面不光滑. 从图6(c)和6(d)可以看出，在各个入射方向上GA的椭偏参量变化同样不是很大，但是较之玻璃基底，变化更明显. 因为玻璃表面本身有一定的粗糙度，而金膜的成膜方式是岛状生长模式，使得金膜表面的粗糙度更大，而椭圆偏振仪对于入射光的微小变化也能敏感捕捉，所以使得玻璃基底上金膜的光学性质在不同入射方向上不同，表现为光学各向异性.

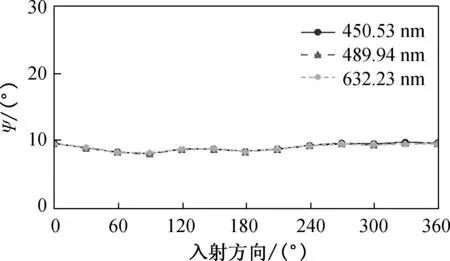
(a) GN的椭偏参量Ψ

(b) GN的椭偏参量φ

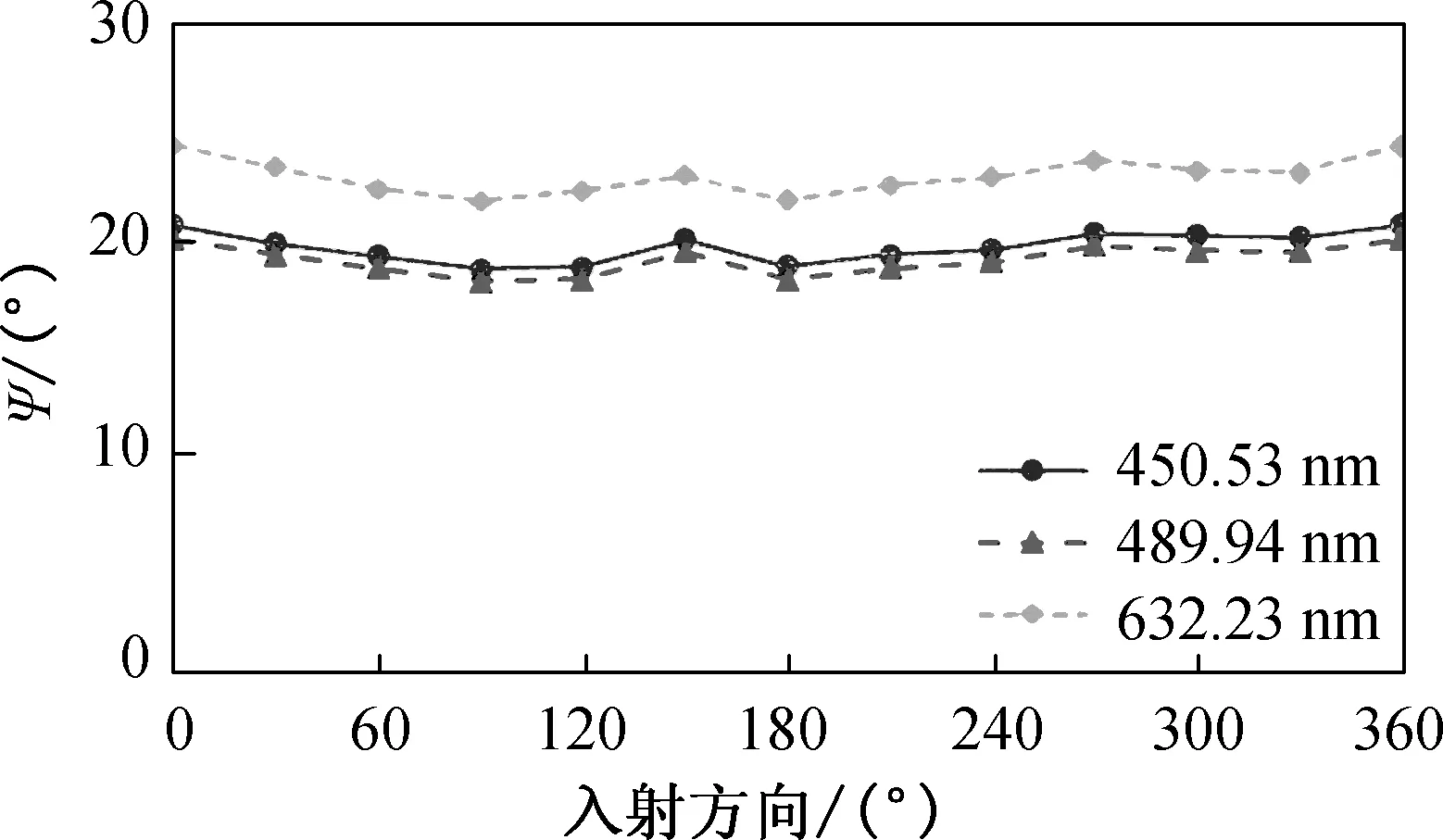
(c) GA的椭偏参量Ψ

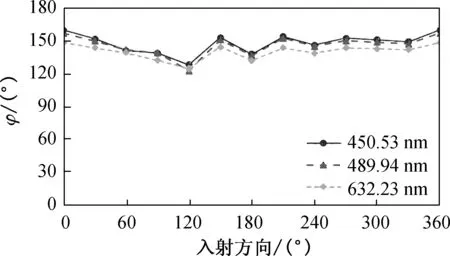
(d) GA的椭偏参量φ

3结语

本文采用直流溅射法在玻璃基底上沉积透明导电金膜，通过调节溅射时间和溅射电流，获得不同厚度的金膜. 利用SEM表征了金膜的表面形貌，四探针测量了金膜的方块电阻，并使用椭圆偏振仪测量了金膜的厚度，以及在不同入射角度和入射方向上透明导电金膜的光学性质，得到了下述结论.

(1) 金膜的厚度随着溅射电流或者溅射时间的增加而增加. 金膜表面的连续性也随着厚度的增加而变得更好，而金膜的方块电阻随着厚度的增加而减小.

(2) 通过分析直流溅射实际沉积的金膜厚度，结合理论膜厚计算公式，发现直流溅射下的透明导电金膜的成膜机理为岛状生长模式.

(3) 利用椭圆偏振仪测量不同厚度金膜的透光率，发现金膜厚度为10～13 nm时，金膜的导电性和透光率均非常优良. 使用椭圆偏振仪测量了不同入射角度和入射方向上透明导电金膜的椭偏参量，对比玻璃基底自身的椭偏参量变化，发现在玻璃基底上的透明导电金膜会表现出各向异性的特征.这是因为玻璃本身表面粗糙度较大，同时金膜以岛状生长模式沉积，这就造成了金膜表面在某种程度上更加粗糙，入射光线经过金膜反射后，金膜表面结构的粗糙造成椭圆偏振仪测量的光学性质呈各向异性.

参考文献

[1] 姜辛，孙超，洪瑞江，等. 透明导电氧化物薄膜[M]. 北京：高等教育出版社，2008：1-2.

[2] BADEKER K. Concerning the electricity conductibility and the thermoelectric energy of several heavy metal bonds[J]. Ann Phys，1907，22(4)：749-766.

[3] 宋健全，刘正堂. 红外增透膜系软件设计及应用[J]. 红外技术，2001，23(2)：1-5.

[4] 章峰勇. 柔性透明导电膜的研究进展[J]. 信息记录材料， 2010,13 (3)：44-51.

[5] 易泰民，邢丕峰，郑凤成，等. 磁控溅射制备纳米厚度连续金膜[J]. 原子能科学技术，2010，44(4)：479-483.

[6] 许小亮，王烨，赵亚丽，等. 磁控溅射法制备的纳米金薄膜的工艺条件和结构分析[J]. 功能材料，2006，37(8)：1216-1219.

[7] 窦娜娜，王涵，张蓓，等. 直流溅射法制备纳米金的工艺及形成机制[J]. 金属热处理，2013，38(8)：14-20.

[8] 陈建林，陈荐，何建军，等. 氧化锌透明导电薄膜及其应用[M]. 北京：化学工业出版社，2011：4-17.

[9] 陈建林. Al 掺杂与 Al-Sc 共掺杂 ZnO 薄膜的制备、微观组织及光电性能[D]. 长沙：湖南大学材料科学与工程学院， 2009.

[10] SMITH D L. Thin-film deposition：Principles and practice[M]. New York：McGraw-Hill，1995.

[11] EL-AGEZ T M， TAYYAN A A E， TAYA S A. Rotating polarizer-analyzer scanning ellipsometer[J]. Thin Solid Films，2010，518(19)：5610-5614.

[12] EL-AGEZ T M， TAYA S A. Development and construction of rotating polarizer analyzer ellipsometer[J]. Optics and Lasers in Engineering，2011，49(4)：507-513.

[13] ELMAN J F， GREENER J， HERZINGER C M， et al. Characterization of biaxially-stretched plastic films by generalized ellipsometry[J]. Thin Solid Films，1998，313(97)：814-818.

[14] SCHUBERT M. Generalized ellipsometry and complex optical systems[J]. Thin Solid Films，1998，313/314：323-332.

[15] JELLISON JR G E. Generalized ellipsometry for materials characterization[J]. Thin Solid Films，2004，450(1)：42-50.

[16] EL-AGEZ T M， TAYA S A. A Fourier ellipsometer using rotating polarizer and analyzer at a speed ratio 1∶1[J]. Journal of Sensors，2010(1)：23-59.

[17] TAYA S A， EL-AGEZ T M， ALKANOO A A. Thin film characterization using rotating polarizer analyzer ellipsometer with a speed ratio 1∶3[J]. Journal of Electromagnetic Analysis and Applications，2011，3(9)：351-358.

文章编号：1671-0444(2016)03-0443-06

收稿日期：2015-04-23

基金项目：国家自然科学基金青年科学基金资助项目(11305035)

作者简介：彭达球(1989—)，男，湖南湘潭人，硕士研究生，研究方向为光电材料与器件. E-mail:pdq889@163.com 施芸城(联系人)，男，副教授，E-mail：sycium@dhu.edu.cn

中图分类号：O 484.5；TN 16

文献标志码：A

Optical Properties of the Transparent Conductive Gold Film Based on Glass

PENGDa-qiu,HUANGXiao-jiang,SHIYun-cheng

(College of Science, Donghua University, Shanghai 201620, China)

Abstract:By using the DC (direct-current) sputtering, different thickness of transparent conductive gold films are deposited based on glass at different sputtering time and current. The thickness and its visible light transmittance, square resistance, surface morphology of the film are measured and characterized by ellipsometer, four-point probe and SEM (scanning electron microscope)，respectively. The results show that the surface of the gold film becomes more continuous and the square resistance decreases with the increase of the thickness. Its conductivity and transmittance perform good when the thickness of gold film between 10 nm and 13 nm. It is not difficult to found that the formation mechanism of the DC sputtering deposition is up to the Volmer-Weber model, according to the results that film’s thickness changes with sputtering conditions and the theoretical calculation formula. By controlling the different incident angles and incident directions of an ellipsometer, and measuring the ellipsometric parameters, the results show that the optical properties of gold film based on glass are very different on variation direction.Key words: direct-current sputtering; transparent conductive gold film; ellipsometer; Volmer-Weber model