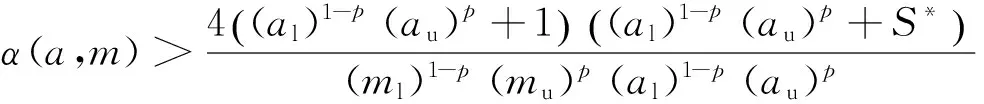具有模糊性的单种群恒化器动力学模型研究

王会姣, 赵　瑜，原三领

(上海理工大学 理学院，上海 200093)



具有模糊性的单种群恒化器动力学模型研究

王会姣, 赵瑜，原三领

(上海理工大学 理学院，上海 200093)

摘要：研究了一类具有模糊性的单种群恒化器模型. 给出了模型依赖于模糊参数p的得失相当常数λ(p)，且模型的动力学完全由λ(p)决定：如果λ(p)<1，微生物绝灭平衡态全局渐近稳定；如果λ(p)>1， 微生物存在的正平衡态全局渐近稳定. 基于上述分析，进而得到了依赖于模糊性的动力学行为的参数空间，并通过数值仿真验证了所得理论结果. 研究结果为预测在模糊参数影响下的恒化器中微生物的演化趋势提供了有效的区间估计方法.

关键词：恒化器； 不确定因素； 区间值参数； 渐近行为

恒化器(chemostat)是实验室中对微生物连续培养的一种装置，在生态学和微生物生态学上具有非常重要的作用. 在生态学上，恒化器可用来模拟海洋和湖泊中单细胞藻类浮游生物的增长过程；在微生物发酵工程方面，它可以看作大型生物反应器的实验室装置. 恒化器有许多优点：在实验室中可以操作，有关参数可以通过实验测得，且所建立的数学模型可以进行较为详尽的数学分析. 因此，对恒化器动力学的建模研究吸引了许多学者的关注，且得到了许多有意义的成果[1-7]. 这些工作在一定程度上为从事生物发酵以及海洋湖泊微生物增长研究的生物工作者提供了可靠的数学依据. 最简单的单营养单种群恒化器模型[4]为

(1)

其中：S(t)和x(t)分别为t时刻恒化器中营养和微生物的浓度. 模型(1)中的所有参数均为正的常数：γ为微生物的增长系数，表示从营养到微生物的转化率；S0为限制性营养的输入浓度；D为稀释率；mS/(a+S)表示Monod型微生物增长的功能反应函数，其中m为微生物的最大增长率，a为半饱和常数. 模型(1)的动力学完全由得失相当常数λ=aD/(m-D)决定：当λ≤S0时，模型(1)存在一个全局稳定的绝灭平衡点E0；当λ>1时，系统存在两个平衡态(绝灭平衡点E0和微生物持续平衡点E*)，其中微生物持续平衡点E*全局渐近稳定，而绝灭平衡点E0不稳定.

模型(1)的参数是基于假设对生物系统和环境参数已经能够准确了解基础上的确定性参数. 然而，由于微生物增长过程非常复杂，要准确测得恒化器中所有的状态变量非常困难. 同时，由于受到操作误差、测量信息缺失等因素的影响，通常测得的模型参数都会落在某一区间范围内而不是精确的固定值[8-10]. 利用模糊微分方程来刻画参数落在某一区间范围的模糊动力学过程已成为一种有效的方法[11]. 例如，文献[8]利用模糊微分方程刻画了一类模糊参数的食饵-捕食模型；文献[9-10]探讨了一类具有模糊区间生物参数的食饵-捕食模型的最佳捕获问题. 受此启发，在模型(1)中考虑其模糊区间的生物参数将更加符合实际情况，所得的模型能够更好地刻画微生物的生长过程. 本文利用模糊微分方程相关的理论和方法来探讨模糊参数对单种群恒化器模型动力学行为的影响.

1模型的建立及预备知识

首先对模型(1)进行无量纲化，令

则模型(1)可写成如下的形式(仍用原来的符号表示各个变量和参数)：

(2)

在模型(2)中将参数m和a用模糊区间值函数的方式进行刻画，即

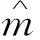
(3)

具有初值：

S(0)≥0,x(0)≥0,

(4)

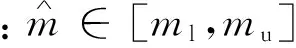
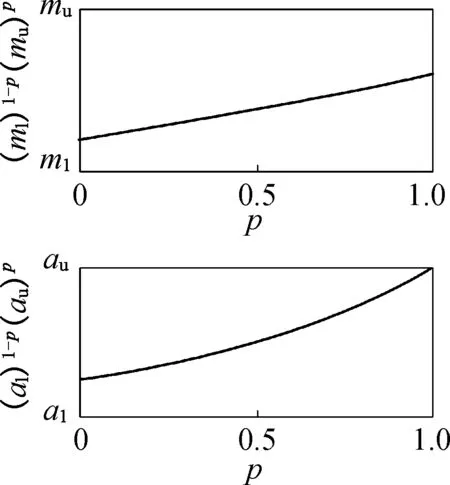
(a) m∧和a∧的变化范围

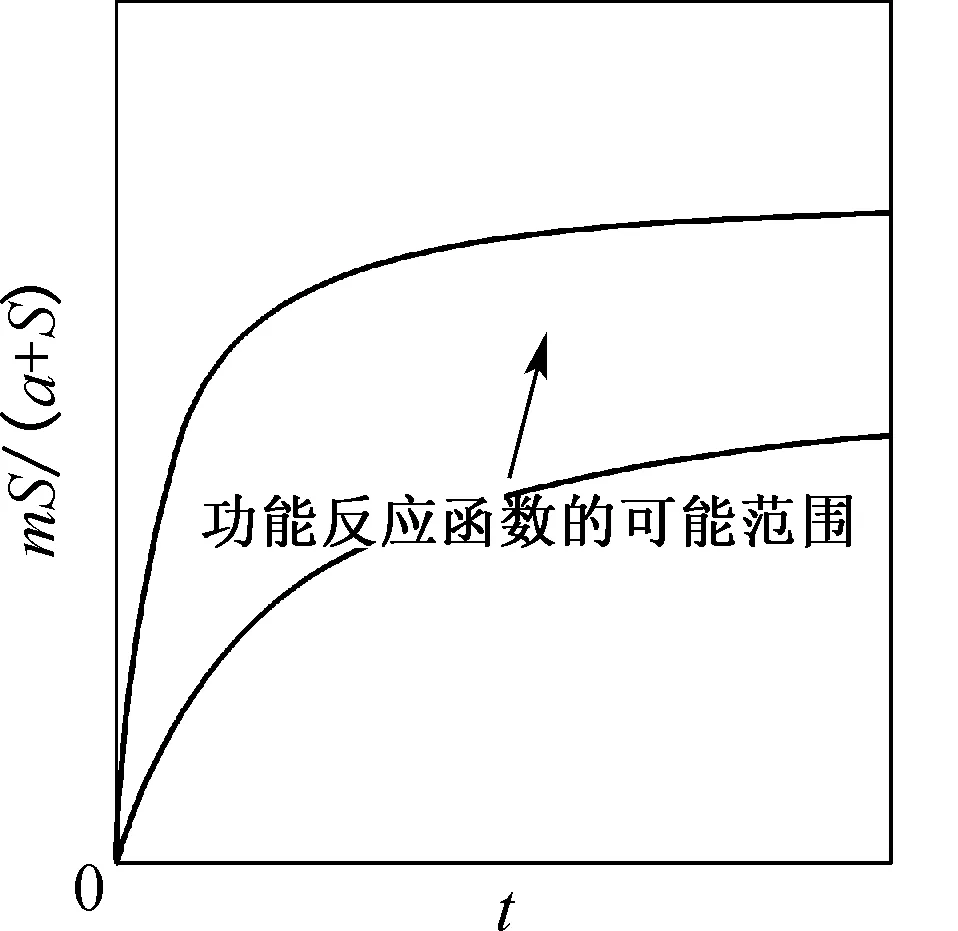
(b) 功能反应函数mS/(a+S)的变化范围

一个区间数B可由闭区间[b,c]表示，并可定义为

B=[b,c]={x:b≤x≤c,x∈R}

其中：b和c分别称为区间数B的左极限和右极限. 对任意的实数b可表示成区间数[b,b].

定义1[7]令b>0，c>0,对区间[b,c]，由于任何实数都可在一条数轴上进行表示，故将区间用一个函数来表示, 则区间[b,c]可表示成如下形式的函数：

h(p)=b(1-p)cp, p∈[0,1]

令B=[bl,bu],C=[cl,cu]为两个区间值，下面给出其运算法则：

(1) 加法.B+C=[bl,bu]+[cl,cu]=[bl+cl,bu+cu]， 其中bl+cl>0. 对应的区间值函数h(p)=(bl+cl)1-p(bu+cu)p,p∈[0,1].

(2) 减法.B-C=[bl,bu]-[cl,cu]=[bl-cu,bu-cl]， 其中bl-cl>0. 对应的区间值函数h(p)=(bl-cl)1-p(bu-cu)p,p∈[0,1].

下面的定理1给出了模型(3)与其区间值函数形式模型(5)的等价性.

定理1模型(3)与下面的区间值函数模型(5)是等价的

(5)

其中：(ml)1-p(mu)p和(al)1-p(au)p(0≤p≤1)分别表示m和a的模糊区间值函数.

证明：模型(3)可写成如下区间值的形式：

(6)

令m1∈[ml,mu],a1∈[al,au]， 根据区间值的运算法则，系统(6)可简化为

(7)

(8)

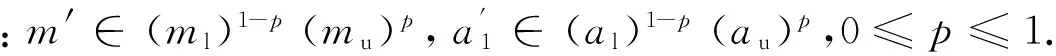
由于模型(5)与模型(3)的等价性,本文主要考虑模型(5)在模糊性条件下的动力学行为.

注1：易知，R={(S,x):S≥0,x≥0,0≤S+x≤1}为模型(3)或(5)的正向不变集.

2模型(5)的平衡态及其全局动力学行为

E*=(S*(p),x*(p))=

(9)

可定义得失相当常数为

(10)

其中：(ml)1-p(mu)p≥1.

注2：如果(ml)1-p(mu)p<1，则微生物的最大增长率小于稀释率，此时,微生物将最终在恒化器中绝灭.

定理2如果λ(p)>1，微生物绝灭平衡态E0=(1,0)全局渐近稳定；如果λ(p)<1，E0=(1,0)不稳定, E*=(S*(p),x*(p))全局渐近稳定.

证明：模型的Jacobi矩阵为

(11)

在平衡点E0=(1,0)处对应的特征方程为

det(J-λI)|E0=(-λ-1)·

(12)

其特征值为

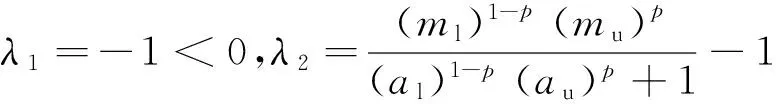
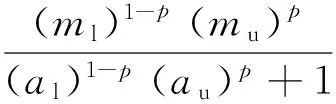
在平衡点E*=(S*(p),x*(p))处对应的特征方程为

(13)

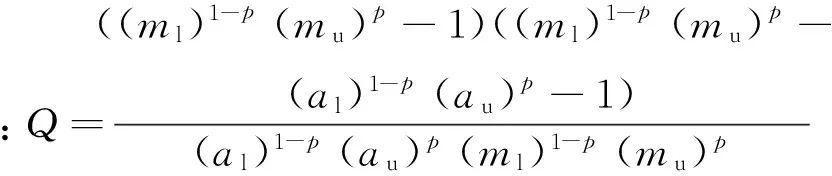
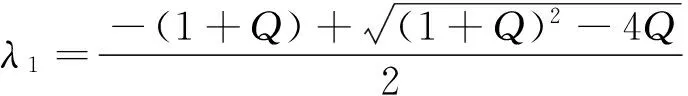
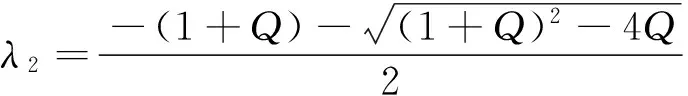
因λ(p)<1，即(ml)1-p(mu)p-(al)1-p(au)p-1>0，可知θ>0. 此时，λ1<0，λ2<0. 因此，E*=(S*(p),x*(p))是局部渐近稳定的结点.

为了证明平衡态E*的全局稳定性，构造如下的Liapunov函数：

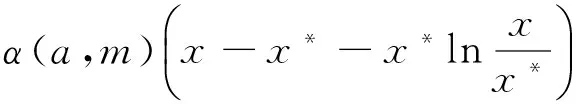
(14)

其中：α(a,m)是关于a和m的正的待定函数. 易知V是正定的. 沿着模型(5)的解计算V的全导数为

(15)

显然，V′(S*,x*)=0. 又因S*+x*=1，有：

(16)

由二次型理论可知, 要使得V′≤0，只需满足

(17)

由式(17)可知

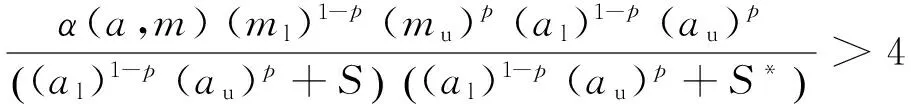
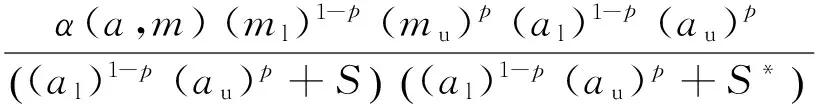
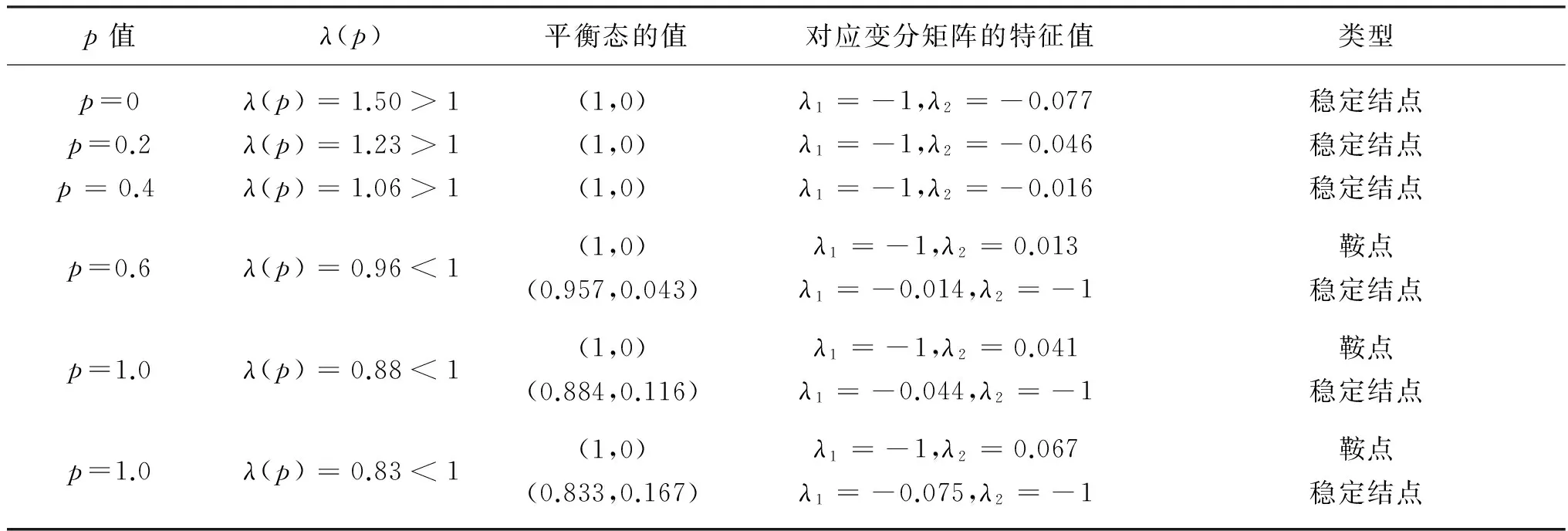
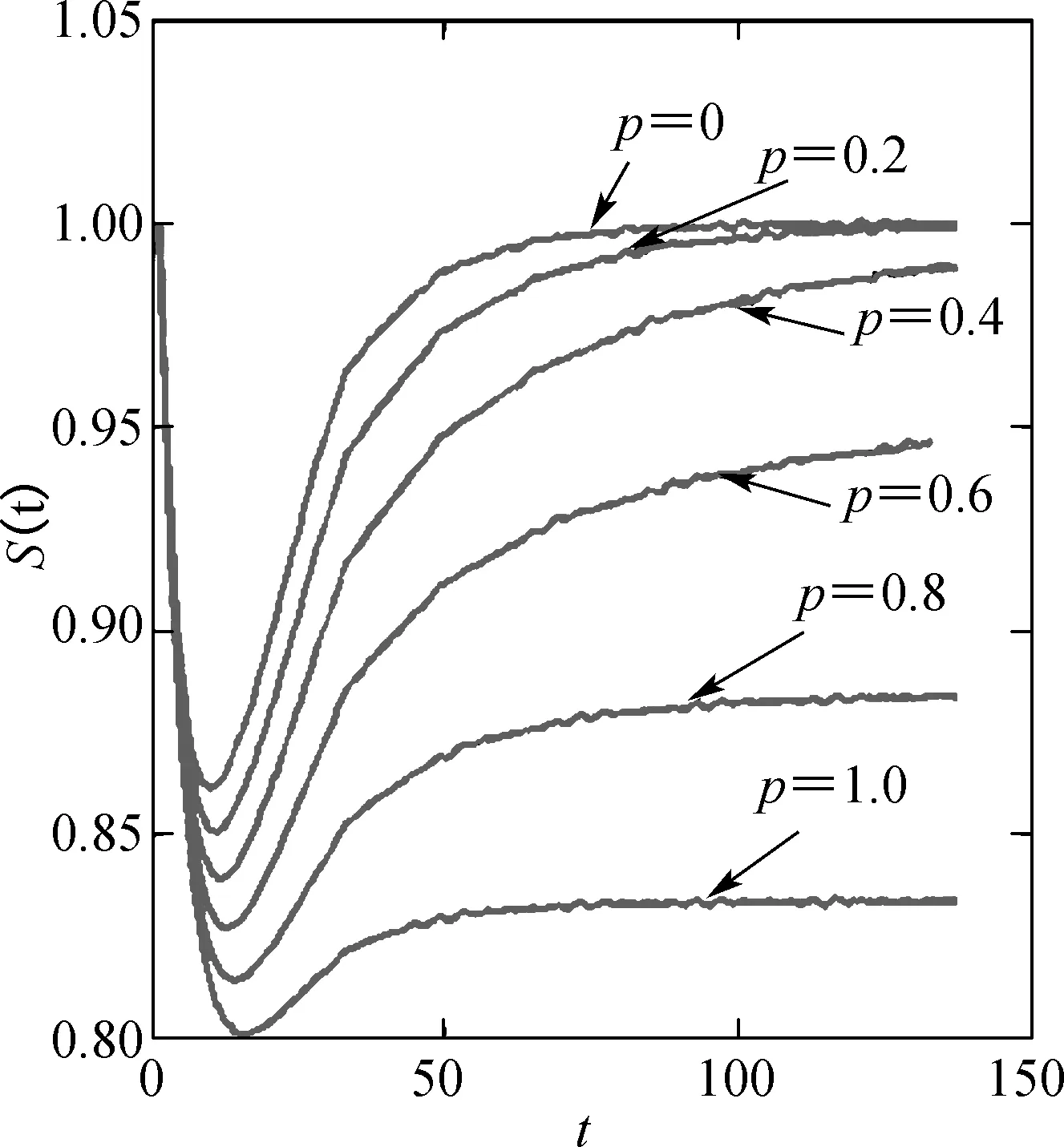
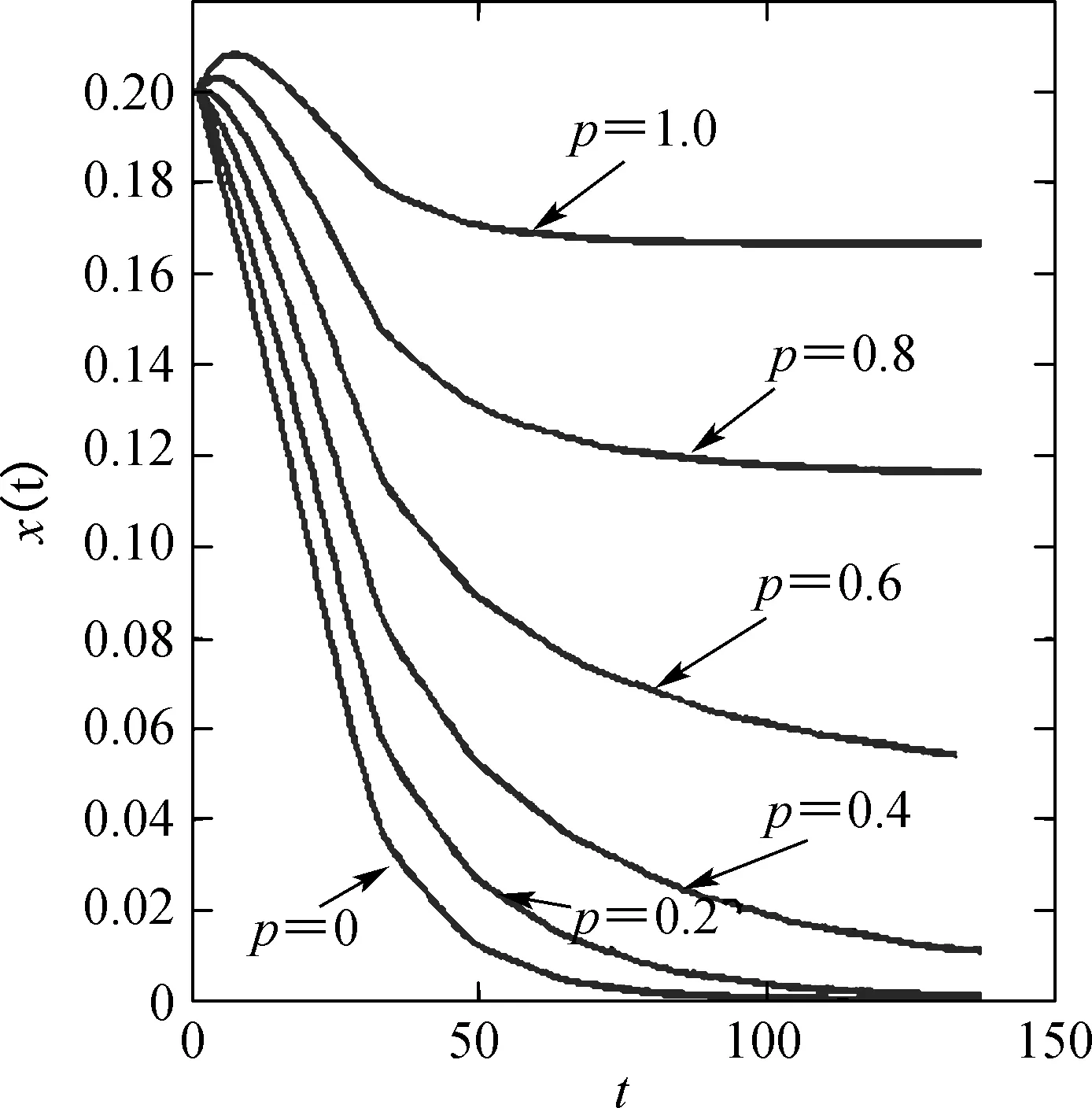
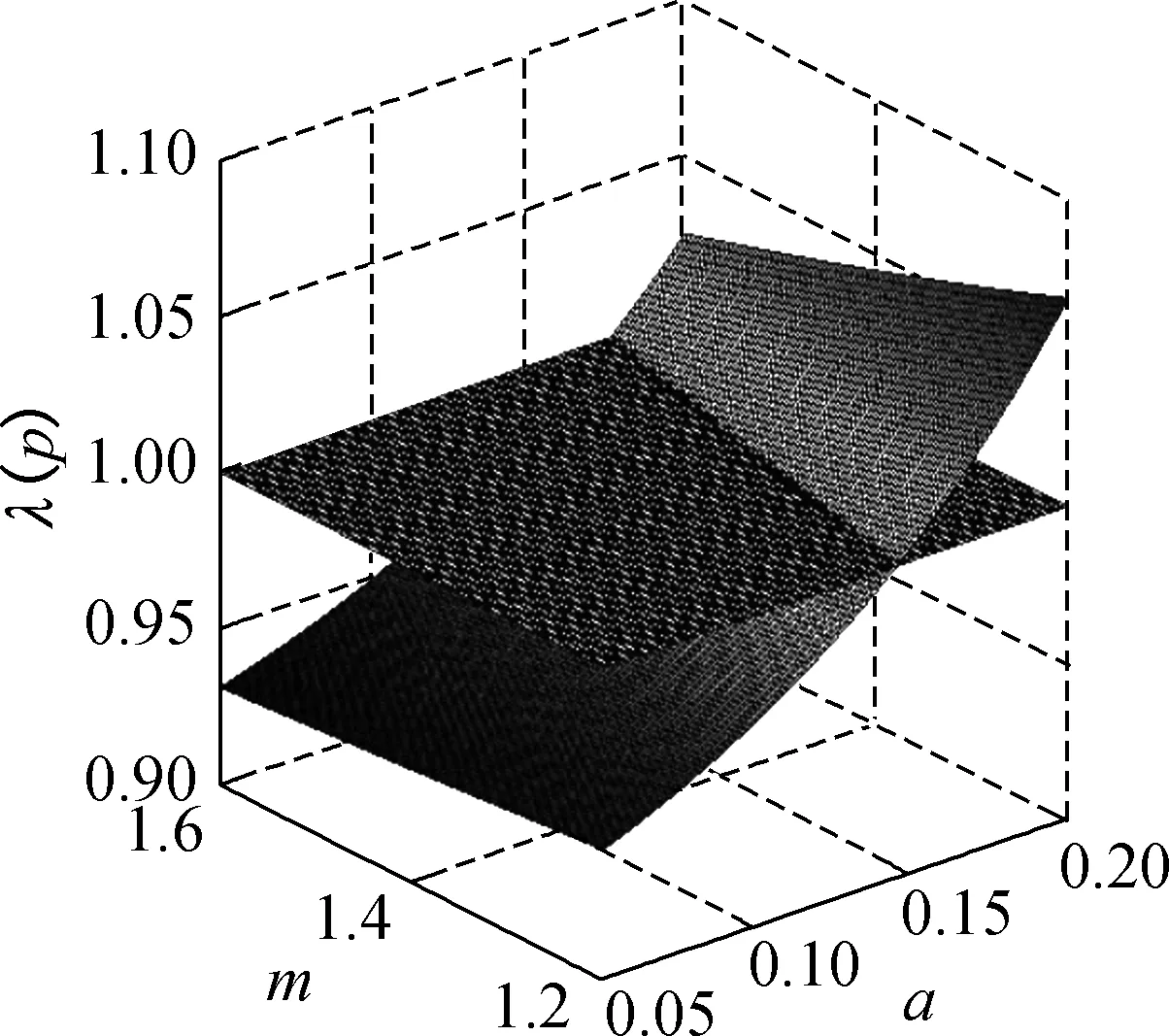
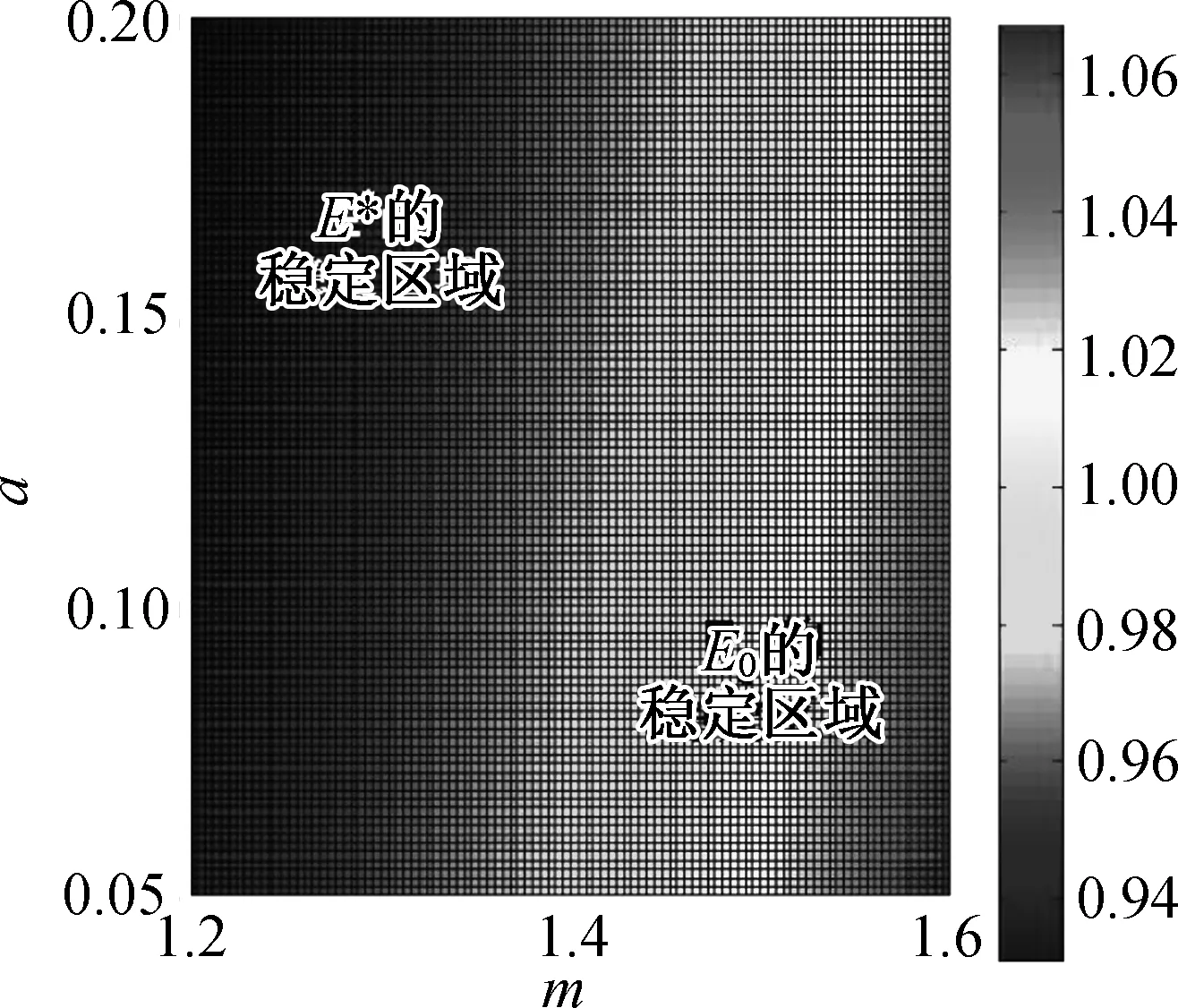
由注1解的正向不变集可知0

因此，使得V′≤0成立的条件为

(18)

即可选择

(19)

使得V′≤0成立. 与此同时，当(S,x)=(S*,x*)时, V′=0.

综述所述，如果λ(p)<1时V′<0，即为E*全局渐近稳定，故定理2得证.

注3：由定理2的证明可知，模型(5)的动力学行为完全由依赖于模糊性的得失相当常数λ(p)决定，模糊性对模型(5)两个平衡态的稳定性具有显著的影响.

3数值仿真及讨论

为了验证本文的理论结果，通过例1说明模糊性对微生物绝灭平衡态和微生物生存平衡态的影响.

例1在模型(5)中，可假定[ml,mu]=[1.2,1.6],[al,au]=[0.3,0.5]. 由于对任意p微生物绝灭平衡态总是存在的，而随着p的变动，微生物生存平衡态会发生较大的改变.对应不同的p值，平衡点及其对应变分矩阵的特征值的变化情况如表1所示.

表1　平衡态的值、其特征值及对应的类型

由表1可知，随着p值的增加，平衡态及其对应的变分矩阵的特征值，以及平衡态的类型都发生了改变. 为了更直观地揭示模糊性对恒化器中单种群微生物的演化趋势的影响，借助Matlab中的ODE45算法，得到不同p值下营养S(t)和微生物x(t)浓度的演化轨线图(如图2所示). 结合表1和图2可知，p值对微生物的生存具有很大的影响：随着p值的增大，原本绝灭的微生物将能够生存下来；另一方面，微生物的演化趋势必将介于p=0和p=1这两条轨线之间，这就为估计恒化器中微生物的演化提供了一种趋势范围的预测手段. 模型的参数由于测量误差、信息缺失等因素而导

致的不确定性是广泛存在的，基于此，本文研究了一类具有模糊参数的单种群恒化器模型，得到了依赖于模糊性的得失相当常数λ(p)的变化对模型动力学行为的影响. 对λ(p)关于模糊参数m和a做敏感性分析，可以得到模型(5)依赖于模糊性的全局动力学行为的参数空间(如图3所示)：如果λ(p)>1，微生物绝灭平衡态是全局渐近稳定的；如果λ(p)<1, 微生物存在平衡态是全局渐近稳定的. 因此，模糊性对单种群恒化器模型动力学行为具有明显的影响. 同时，本文的方法能够为估计在模糊参数影响下的恒化器中微生物的演化趋势提供有效的区间估计方法.

(a) S(t) 　　　　(b) x(t)

(a) λ(p)对m和a的敏感性分析　　　　(b) E0和E*的稳定区域

4结语

本文得到了单种群恒化器模型的动力学行为完全由依赖于模糊性参数p的得失相当常数λ(p)决定的结论，即：如果λ(p)>1，微生物绝灭平衡态全局渐近稳定；如果λ(p)<1，微生物存在的正平衡态全局渐近稳定.而考虑到实际中参数的不确定性，故对模糊性的动力学行为的研究更为符合实际，并且其研究结果为预测在模糊参数影响下的恒化器中微生物的演化趋势提供了有效的区间估计方法. 下一步的研究应在更多的生物模型领域考虑模糊参数的影响.

参考文献

[1] SMITH H L, WALTMAN P. The theory of the chemostat: Dynamics of microbial competition[D]. Cambridge: Cambridge University Press, 1995.

[2] 陈坚, 李寅. 发酵过程优化原理与实践[M]. 北京: 化学工业出版社, 2001.

[3] 阮士贵. 恒化器模型的动力学[J]. 华中师范大学学报(自然科学版), 1997, 31(4): 377-397.

[4] GARD T C. A new Liapunov function for the simple chemostat[J]. Nonlinear Analysis: Real World Applications, 2002 (3): 221-226.

[5] 李姣, 孟琳琳. 具有多个参数扰动的随机恒化器模型研究[J]. 上海理工大学学报，2013, 35(6): 523-530.

[6] 凌志超, 张天四. 恒化器中一类具有非常数消耗率微生物培养模型的定性分析[J]. 上海理工大学学报，2010, 32(6): 539-548.[7] XU C Q, YUAN S L, ZHANG T H . Asymptotic behavior of a chemostat model with stochastic perturbation on the dilution rate[J]. Abstract and Applied Analysis, 2013, DOI：10.1155/2013/ 423154.[8] PEIXOTO M S, BARROS L C, BASSANEZI R C. Predator-prey fuzzy model[J]. Ecological Modelling, 2008, 214(1): 39-44.[9] PAL D, MAHAPTRA G S, SAMANTA G P. Optimal harvesting of prey-predator system with interval biological parameters: A bioeconomic model[J]. Mathematical Biosciences, 2013,241 (2): 181-187.

[10] ZHANG X B, ZHAO H Y. Bifurcation and optimal harvesting of a diffusive predator-prey system with delays and interval biological parameters[J]. Journal of Theoretical Biology,2014，363: 390-403.

[11] LAKSHMIKANTHAM V, MOHAPATRA R N. Theory of fuzzy differential equations and inclusions[M]. London:Taylor & Francis, 2003.

文章编号：1671-0444(2016)03-0437-06

收稿日期：2015-06-24

基金项目：国家自然科学基金资助项目(11271260)；上海市教委科研创新重点资助项目(13ZZ116)；中国沪江基金资助项目(B14005)；上海市一流学科资助项目(XTKX2012)

作者简介：王会姣(1988—)，男，河北邢台人，硕士研究生，研究方向为生物数学.E-mail:13167051881@163.com 原三领(联系人), 男，教授，E-mail: sanling@usst.edu.cn

中图分类号：O 159

文献标志码：A

Study on the Dynamics of a Single-Species Chemostat Model with Fuzziness

WANGHui-jiao,ZHAOYu,YUANSan-ling

(College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China)

Abstract:A single-species chemostat model with fuzziness is considered. The break-even concentration λ(p)，which depends on the fuzzy parameter p is first given, and the dynamics of the model is completely determined by λ(p): if λ(p)>1， then the extinction equilibrium is globally stable; if λ(p)<1， then the positive equilibrium of microorganism survival is globally stable. Based on the above analysis, the parameter space of dynamic behaviors which depend on the fuzziness is derived. Numerical simulations are carried out to support the theoretical results obtained. The research result provides an effective method on the prediction of the evolution ranges of the microorganism in chemostat under the influence of fuzzy parameters.

Key words:chemostat; uncertain factors; interval-valued parameters; asymptotic behavior