FRP管-混凝土-钢管复合套管约束性能有限元分析
张 俊 林, 任 慧 韬, 王 苏 岩
( 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024 )
FRP管-混凝土-钢管复合套管约束性能有限元分析
张 俊 林,任 慧 韬*,王 苏 岩
( 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连116024 )
摘要:为了研究FRP管-混凝土-钢管复合套管的约束性能,采用修正的Hognestad表达式来描述混凝土单轴受压应力-应变关系,利用ABAQUS软件对FRP约束混凝土短柱轴压试验进行有限元模拟,并与试验结果进行了比较,表明有限元模型通过精确定义材料参数、单元模型、表面作用、边界条件,可准确描述FRP约束混凝土短柱力学性能.在此基础之上,分析了FRP管-混凝土-钢管复合套管中3种材料厚度变化对管约束性能的影响.结果表明,在复合套管的约束作用下,核心混凝土的轴向应力-应变曲线呈现双线性的特点,复合管中的钢管主要影响第一线性段,而FRP管和混凝土主要影响第二线性段.该结论为今后进行该类组合柱的研究提供了参考.
关键词:FRP;复合套管;有限元方法;应力-应变关系
0引言
由于FRP(fiber reinforcement polymer)材料具有抗拉强度高、自重轻、耐久性好、施工方便、弹性模量小、热膨胀系数与混凝土相近等优点,可以有效延长恶劣环境下混凝土结构的耐久性和服役寿命,因此被广泛地运用到工程实践当中.将FRP材料与混凝土、钢材等传统建筑材料结合形成的组合构件可以充分发挥各种材料的优势,从而增强结构的承载力和延性,延长建筑物的寿命.近年来,由Teng等提出的FRP-混凝土-钢管组合柱(DSTC)[1]成为其中典型的代表,因此对该类组合构件力学性能的研究成为人们关注的重点.而对于大型柱体,空心的DSTC显然不能满足承载力的要求.基于此,本课题组提出可以将FRP管-混凝土-钢管作为预制复合套管,让其主要发挥约束作用,同时充当施工模板,在其内部填充混凝土,以此形成承载力更强的组合柱,可以应用在大型柱体或处于恶劣环境的桥墩中.之前刘玉雷[2]已做过相关试验研究,本文将主要运用ABAQUS软件进行相关的有限元分析.
人们进行了大量的试验来探寻FRP约束混凝土柱在轴压、偏压、受弯、单调荷载以及循环往复荷载等作用下的力学性能,并提出了合理的混凝土轴向应力-应变模型,可以对混凝土在FRP约束作用下的极限强度和极限应变进行准确预测.但是,运用有限元软件对此类组合柱进行数值模拟做得并不多,而在进行有限元模拟时,对混凝土单轴本构模型的合理选取是保证模拟结果较为准确的关键.已有的研究中,Yu等[3-4]分别利用ABAQUS软件中的D-P塑性模型和塑性-损伤模型(CDPM)对FRP约束混凝土进行了有限元模拟,其提出了一种改进的CDPM,对损伤因子、应变硬化/软化规律和流动法则进行了全面细致的说明,并编译了定义材料属性的子程序,最后得到较准确的数值模拟结果.但是论文里对于无约束混凝土的单轴受压应力-应变模型的选择并未多做说明.陆新征等[5]和余小伍[6]分别利用ANSYS 软件和ABAQUS软件对FRP约束混凝土柱轴压试验进行了模拟,无约束混凝土的单轴受压应力-应变表达式前者选用的是过镇海等人的表达式,而后者选用的是Saenz等人的表达式.从模拟结果来看,二者得到的约束混凝土轴向应力-应变曲线与试验值并不是特别吻合.
韩林海[7]通过对大量钢管混凝土轴压算例的计算分析,在普通混凝土单轴受压应力-应变关系模型的基础上,考虑约束效应系数的影响,提出了适用于ABAQUS有限元分析的核心混凝土应力-应变关系表达式,并得到了广泛运用.类似地,本文通过对文献[8]中的4种混凝土单轴受压应力-应变曲线的综合比较分析,采用稍作改动的Hognestad表达式对FRP约束混凝土柱轴压试验进行有限元模拟.同时在此基础上,分析FRP管、钢管和混凝土3种材料的厚度变化对复合套管约束性能的影响.
1本构模型与材料参数设定
1.1FRP管与钢管
目前应用较广的钢筋本构模型有理想弹塑性模型、三折线模型、全曲线模型和双线性模型,在本文的有限元模拟中对钢管采用理想弹塑性模型,泊松比为0.3.
对于FRP这种正交异性材料,由于受压时其轴向压应力与环向拉应力相比基本可以忽略,一般处理方法是假定FRP管只具有环向刚度,采用线弹性的材料模型模拟.在ABAQUS中的材料参数设定页面勾选“No Compression”选项,不考虑其受压.
1.2混凝土
ABAQUS中提供了多种可以用来描述混凝土的本构模型,主要有4种:混凝土损伤塑性模型(concrete damaged plasticity model)、弥散裂纹模型(smeared model)、脆性破裂模型(brittle cracking model)和Cap.其中,混凝土损伤塑性模型同时采用弹性损伤和塑性变形的概念来模拟混凝土的非线性性能[9].该模型采用一个标量损伤变量定义弹性损伤;采用Lee等[10]提出的屈服准则定义屈服面;采用Drucker-Prager双曲型势函数定义非关联流动法则,用于混凝土结构的各种荷载分析,如单调加载、循环加载和动力加载等,本文亦采用此种模型模拟混凝土材料.
从已有的试验研究可以看出,FRP约束混凝土的应力-应变曲线呈现典型的抛物线加直线的特征,因此综合比较之下,本文采用略作改动的Hognestad表达式来模拟混凝土的单轴受压应力-应变关系,具体表达式如式(1)和(2):
抛物线段,当0<εc≤ε0时,
(1)
直线段,当ε0<εc时,
(2)
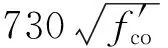
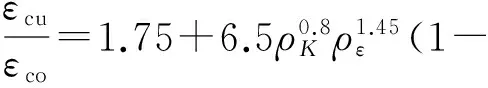
(3)
式中:εco=0.002,ρK=EFRPtFRP/(EsecoRo),ρε=εh,rup/εco,Eseco=f′co/εco,φ为空心率,Ro为受约束混凝土半径.
2有限元模型的建立
根据FRP管-混凝土的组成和受力特性,采用三维实体单元模拟混凝土,由于模型中涉及FRP管与混凝土、混凝土与钢管不同形式的接触,而多接触模型的最大问题就是收敛性较差,因此在选取各种模型的时候采用收敛性较好的一次单元.混凝土采用减缩积分的八节点六面体完全积分单元(C3D8R),其对于三维问题可以以最低的成本得到最好的结果;FRP管采用四节点膜单元(M3D4R),在ABAQUS/standard中,膜单元只有面内刚度,没有抗弯刚度;钢管采用四节点常规壳单元(S4R),此种单元性能稳定,适用范围很广.
在本文的模型中,采用ABAQUS中的Mesh Tie Constraint选项模拟FRP管和混凝土的界面,即认为FRP管内表面和混凝土外表面共节点,轴向位移完全一致,无相对滑动.对于混凝土和钢管之间的接触,则采用Contact Pairs选项进行模拟,该选项允许两个表面相互分离,并能在两个表面相互接触时自动计算法向压应力,一般选取刚度较大的材料作为主面,反之为从面.定义Contact Pairs时包括切向行为和法向行为两个子选项,法向行为选择“硬”接触,勾选“允许接触后分离”,切向行为只需输入合理的摩擦因数即可,其他可遵循软件默认设置.
对短柱进行位移加载控制,柱端进行固定约束,适当调整增量步大小,有限元模型网格划分如图1所示.在计算过程中若FRP管环向应变达到由试验测得的断裂应变,则认为达到破坏极限状态.
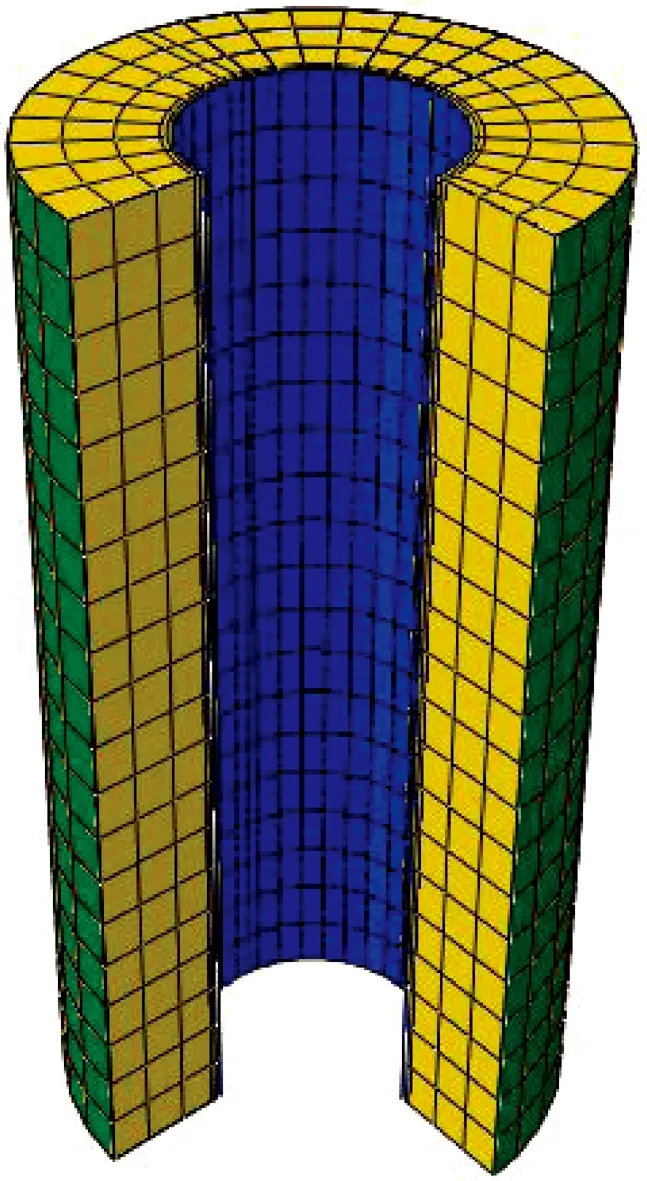
图1 ABAQUS有限元模型网格划分
3试验概况
本文对文献[1]、[2]和[12]中的4组共9个试件进行了有限元模拟.其中,D37、DSB和FCC试件高305 mm,外直径152 mm.PT-40-全和PT-40-核心试件高600 mm,外直径210 mm,均进行轴心受压试验,各试件的具体数据见表1.
表1中,f′co为无约束混凝土圆柱体的轴心抗压强度,其中PT-40组试件中27.2 MPa为核心混凝土强度,夹层混凝土强度为32.3 MPa;Ds和ts分别为钢管的外直径和厚度;Es为钢管的弹性模量;fy为钢管的屈服强度;tFRP为外包FRP管的厚度;EFRP为FRP管环向弹性模量;εcu为试件的轴向极限应变;εh,rup为FRP断裂时的环向应变(下同).
值得说明的是,4组试件中,D37和DSB系列试件均为FRP管-混凝土-钢管空心短柱;PT-40-全和PT-40-核心试件为FRP管-混凝土-钢管-混凝土实心短柱.前者为全截面加载,后者为核心加载,当FRP管环向应变达到断裂应变时认为试件破坏.而FCC试件为FRP管-混凝土实心短柱,并作为DSB系列试件的对照.由于未找到FCC试件破坏时FRP的断裂应变,在之后的模拟中,此试件以达到与试验一致的轴向极限应变作为其破坏标志.所有的试验中,FRP的弹性模量和断裂时的环向应变均由FRP片状试件的拉伸试验测得.

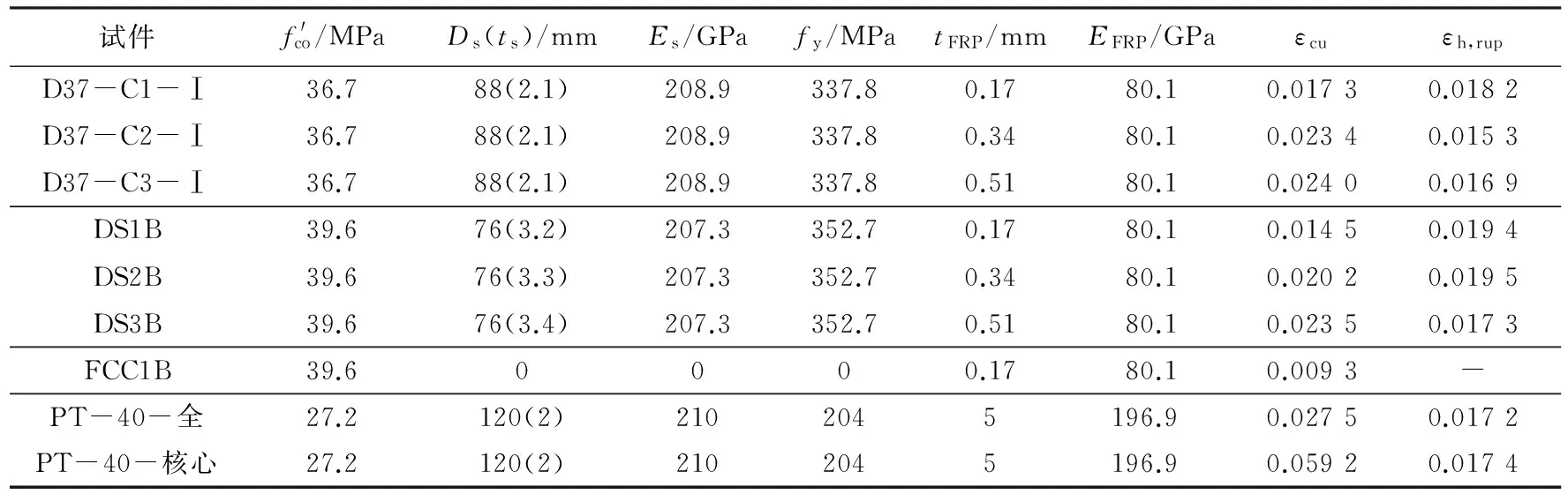
表1 试件参数
4模拟结果与试验结果的比较
4.1荷载与轴向应变曲线
图2给出了有限元计算得到的FRP管-混凝土-钢管轴压短柱荷载-轴向应变曲线与试验结果的对比,其中实线为试验数据,虚线为模拟数据.可见,有限元模拟结果与试验结果吻合较好.表2给出了模拟与试验所得到的极限承载力和轴向极限应变的对比结果.从表中可以看出,除了D37-C2-Ⅰ试件的轴向极限应变偏差较大以外,有限元模拟得到的结果与试验相比较非常接近.而造成这种偏差的原因很有可能是试验试件太少,数据比较离散,从而导致获取的该试件发生破坏时FRP的断裂应变偏小.同时也可以看出,随着FRP管厚度的增大,即侧向约束的增强,FRP管-混凝土-钢管轴压短柱的极限承载力和轴向极限应变也随着增大,也体现出该种组合柱充分发挥各种材料优势的特点.

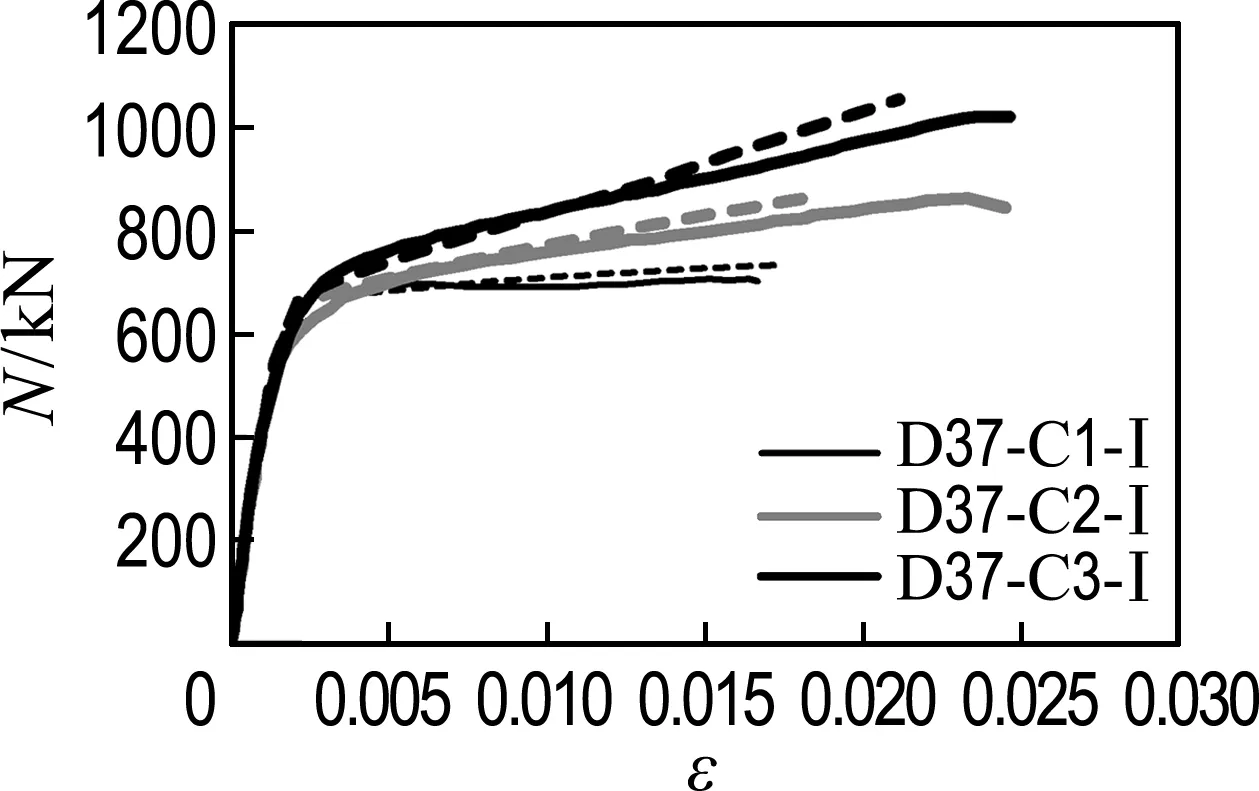
(a) 试件1组
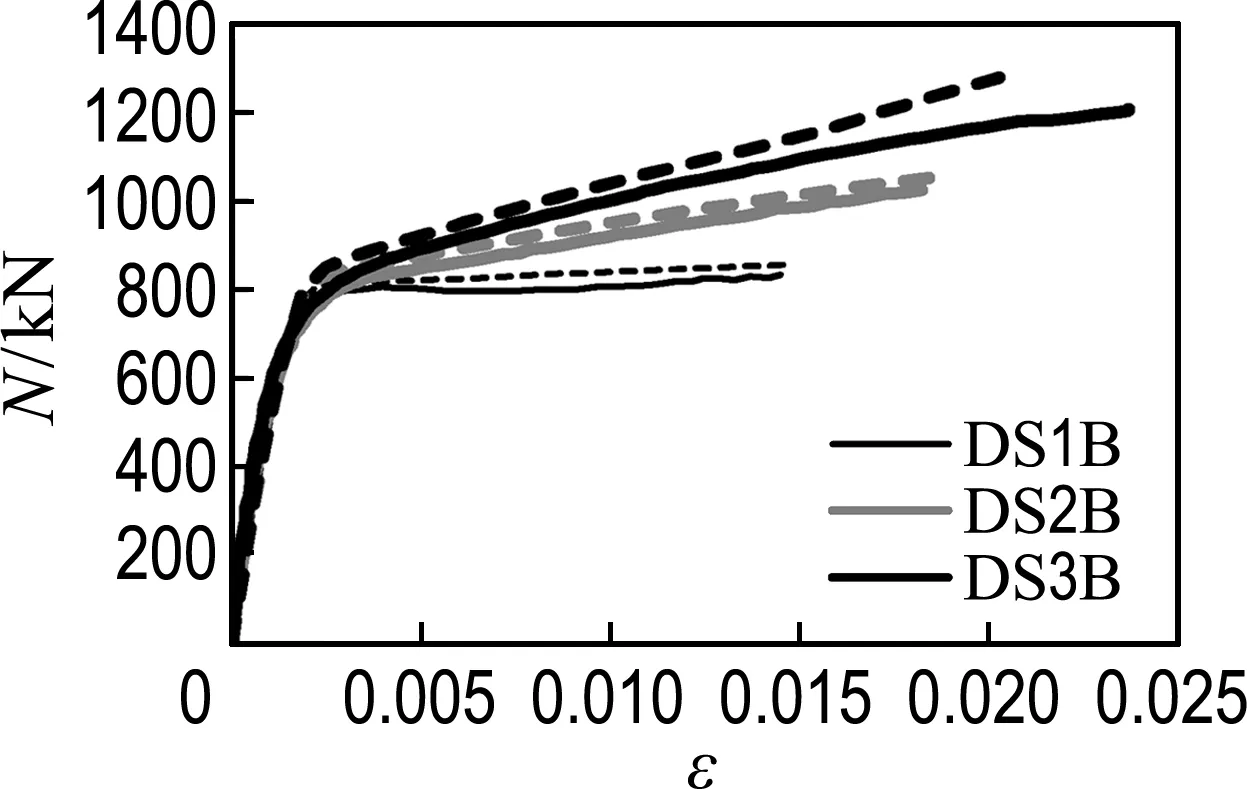
(b) 试件2组
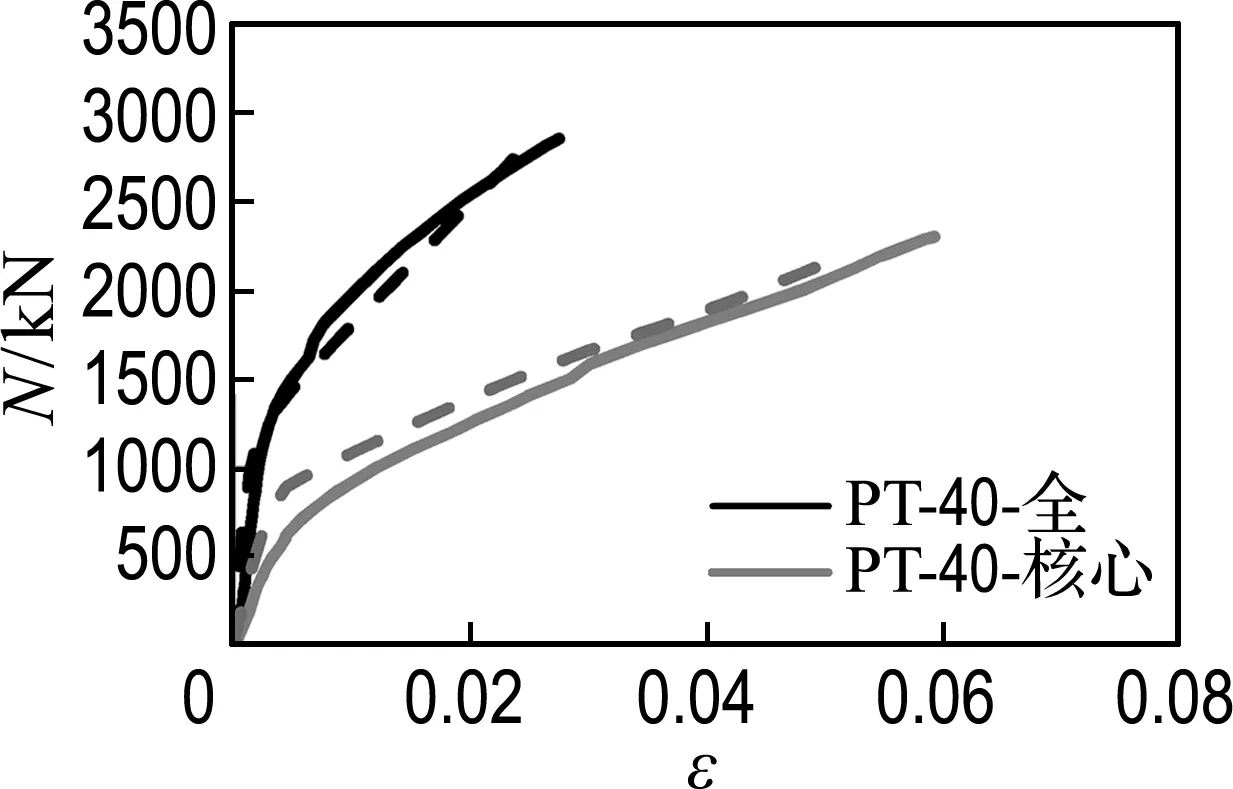
(c) 试件3组
图2试件荷载-轴向应变曲线
Fig.2The load-axial strain curve of specimens
4.2混凝土应力-应变关系
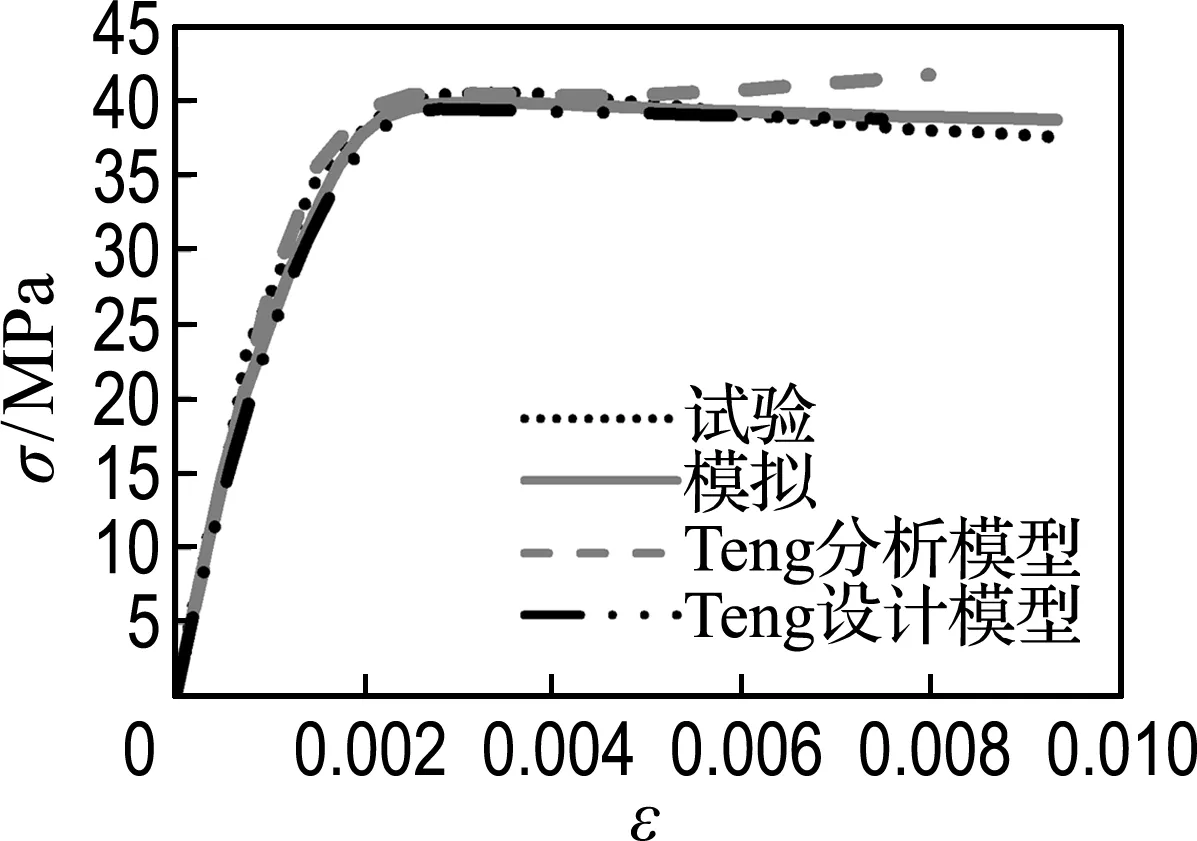
对于FRP约束混凝土,核心混凝土的轴向应力-应变关系一直以来都是研究的重点.长期以来,人们提出了许多模型来预测混凝土受FRP约束作用下的应力-应变关系.其中最具代表性的是文献[13]提出的基于分析的应力-应变模型和文献[14]提出的基于设计的应力-应变模型.因此,本文也从有限元模拟中提取混凝土的轴向平均应力-应变曲线,并与试验数据以及根据两种应力-应变模型计算出的数据进行了对比,结果如图3所示.
图中横坐标代表混凝土的轴向平均应变,由试件位移除以柱高得到;纵坐标代表混凝土的平均应力,由混凝土承担荷载除以混凝土截面面积得到,对于FRP管-混凝土-钢管空心组合柱(D37和DSB试件),混凝土承受的荷载假定等于整个试件所承受荷载减去相同轴向应变下空钢管受压试验所测得的荷载.当轴向应变超过空钢管受压试验所得极限应变时,考虑混凝土的约束作用,假定钢管所承受荷载等于空钢管的极限承载力.需要指出的是,该假定忽略了组合柱中钢管在混凝土约束下所承受荷载和钢管试验所测得荷载的差异.
从图中可以看出,FRP约束混凝土轴压短柱中混凝土的应力-应变曲线呈现典型的抛物线加直线的特征.加载初期由于混凝土侧向膨胀较小,且各部分材料均处于弹性变形阶段,FRP管并不能对混凝土提供有效约束作用,使得混凝土应力-应变曲线出现与无约束轴压情况近似的抛物线段;随着混凝土内部微裂缝迅速开展,侧向变形增大,FRP管发挥有效的约束作用,试件的承载力和延性增大,因此混凝土应力-应变曲线进入上升的直线段.同时还可看出,随着FRP约束的增强,核心混凝土的极限强度和极限应变也随之增大.ABAQUS有限元模拟结果与试验结果以及Teng分析模型计算出的结果十分吻合,验证了该有限元模型的正确性,而下文也根据该模型对复合套管的约束性能进行分析.

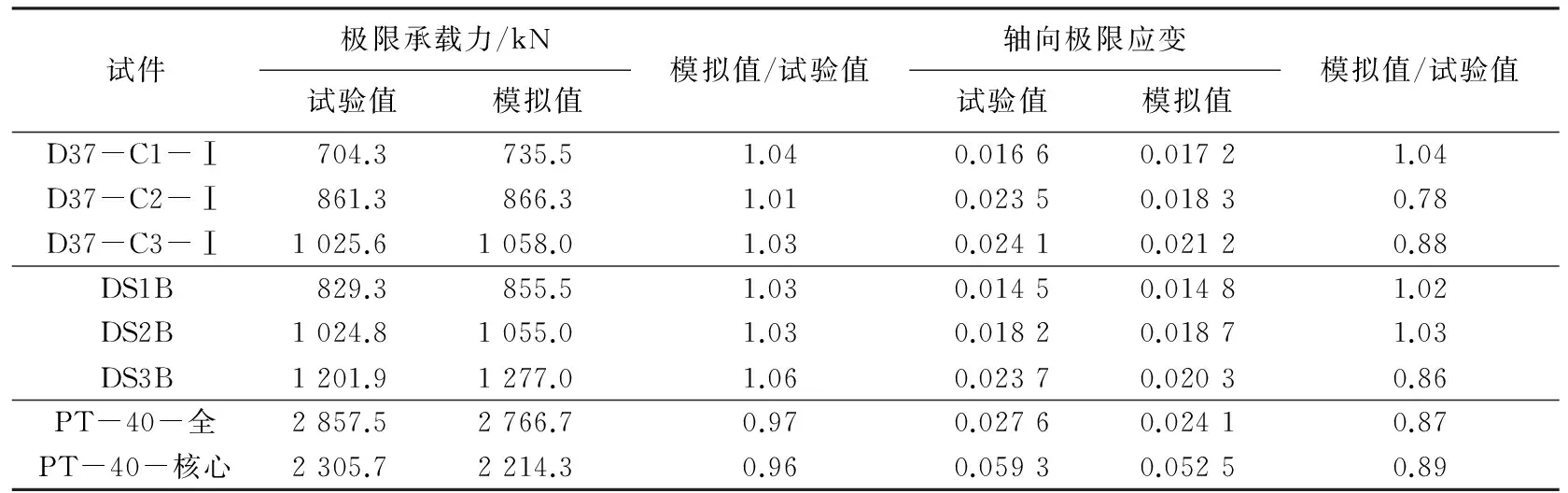
表2 极限承载力和轴向极限应变模拟值与试验值比较

(a) FCC1B

(b) D37-C1-Ⅰ

(c) DS1B
图3混凝土轴向平均应力-应变曲线
Fig.3The axial average stress-strain curve of concrete
5材料厚度变化对复合套管约束性能影响分析
基于以上有限元分析,为了了解材料厚度变化对复合套管约束性能的影响,参照PT-40-核心试件的各材料参数,进行了3组试件的数值分析,内层核心混凝土柱统一为柱高600 mm,直径160 mm,混凝土强度均为C40,采用核心加载.各组试件的具体情况见表3.
对于核心加载情况,图4反映了各材料厚度变化时,核心混凝土轴向平均应力-应变曲线的变化趋势,从中可以发现,3种情况下复合管的约束性能呈现完全不一样的规律,结论如下:(1)随着FRP管厚度的增大,约束作用明显增强.核心混凝土的抗压强度和极限应变均增大,轴向平均应力-应变曲线终点向右上方移动,曲线第一线性段和拐点位置保持一致,而第二线性段的斜率逐渐增大,如图4(a)所示.(2)随着钢管厚度的增大,约束作用明显增强.核心混凝土的极限应变基本一样,抗压强度明显增大,轴向平均应力-应变曲线第一线性段逐渐延长,拐点位置向右上方移动,第二线性段斜率相同,如图4(b)所示.(3)随着混凝土厚度的增大,核心混凝土的抗压强度基本一样,有略微减小,极限应变明显增大,轴向平均应力-应变曲线第一线性段与拐点位置保持一致,第二线性段的斜率逐渐减小.而且在加入钢管之后,约束效果明显比仅有FRP管时强,如图4(c)所示.

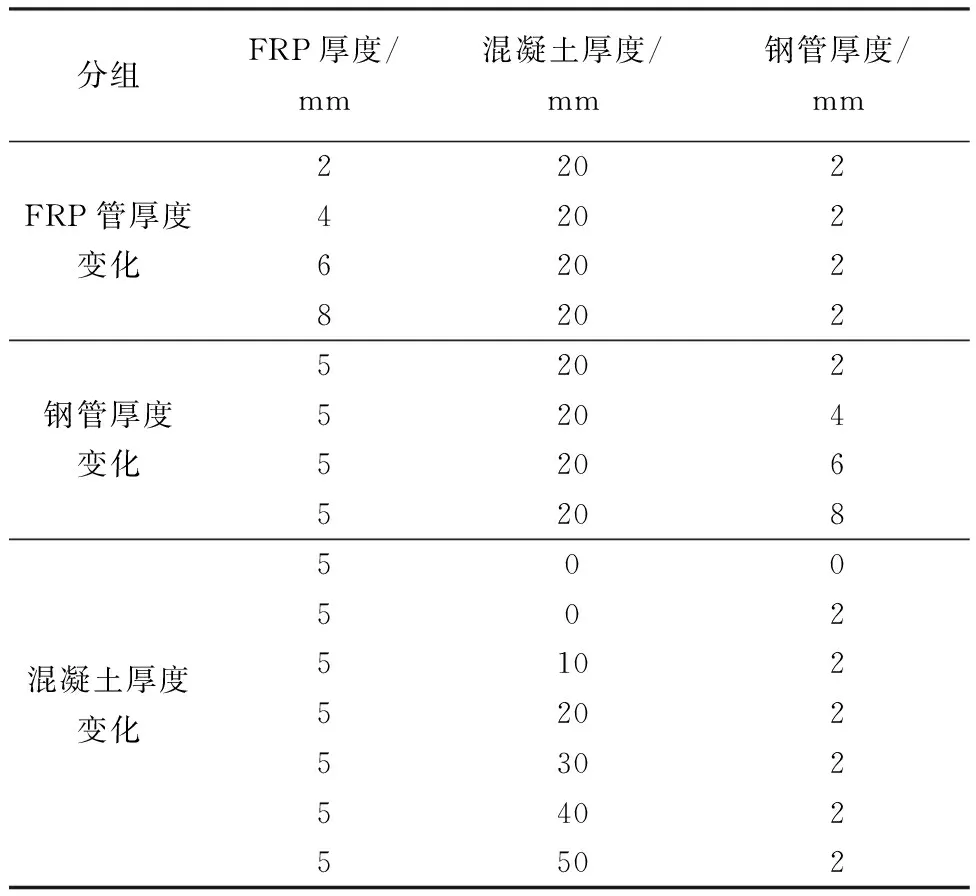
表3 各组复合管的具体参数


(a) FRP管厚度变化
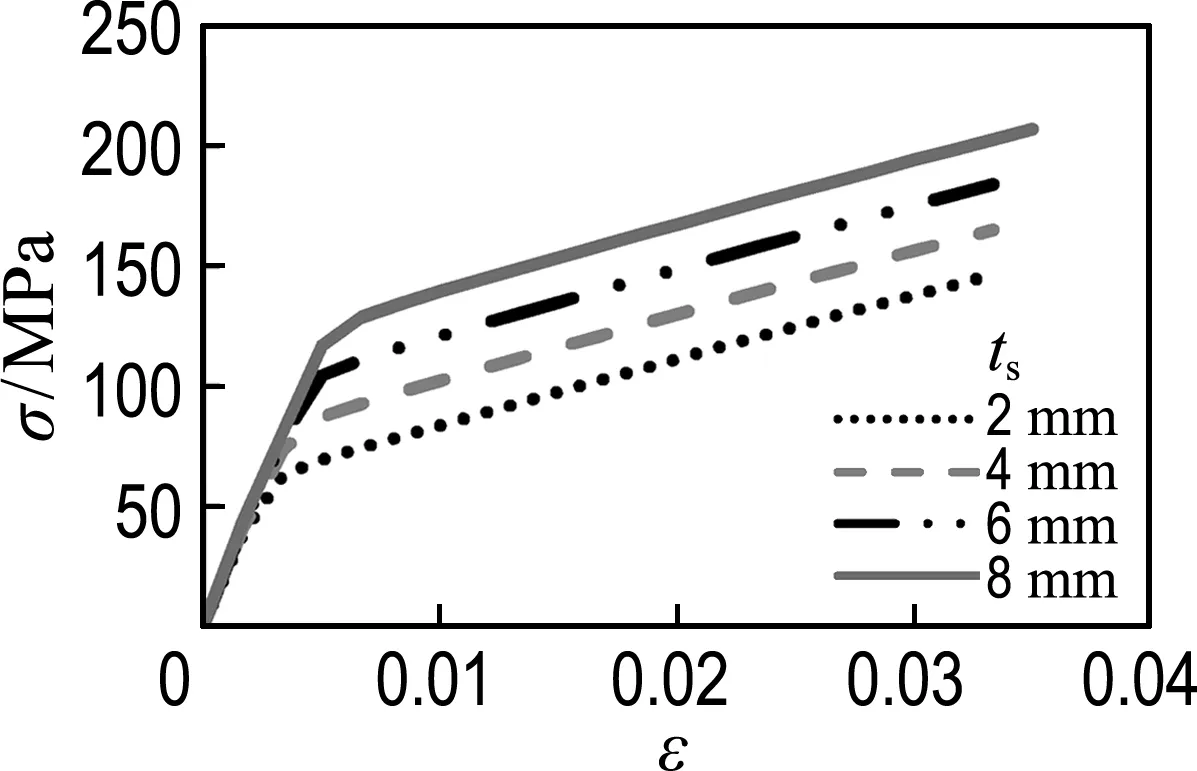
(b) 钢管厚度变化
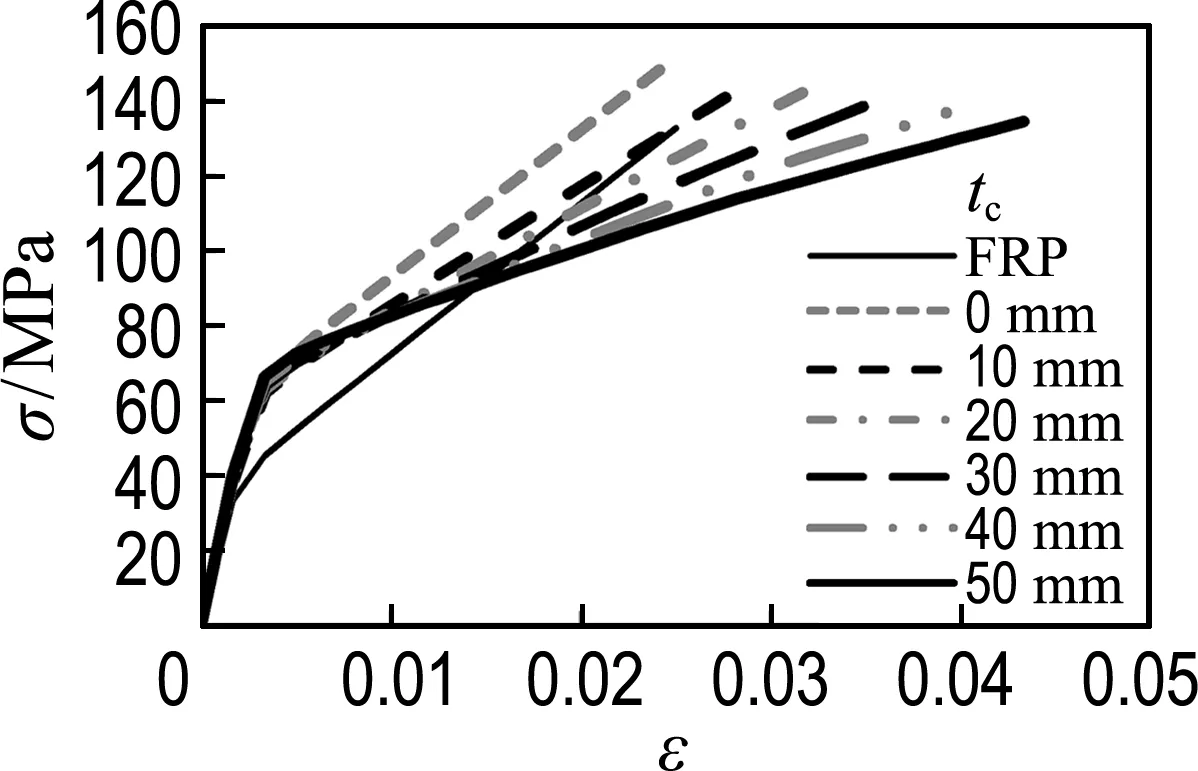
(c) 混凝土厚度变化
图4各材料厚度变化时核心混凝土轴向平均应力-应变曲线
Fig.4Theaxialaveragestress-straincurveofcoreconcretewhilethethicknesschanges
分析其原因,一是与3种材料自身的性质有关,二是与复合管的工作机制有关.随着加载的进行,核心混凝土侧向膨胀逐渐增大,层层向外,钢管为第一重约束,不考虑混凝土受拉,FRP管为第二重约束,复合管中各种材料产生约束作用在时间上呈现先后顺序,这也解释了对于核心混凝土轴向平均应力-应变曲线,钢管的性质主要影响第一线性段,而混凝土和FRP管主要影响第二线性段.
6结论
(1)该有限元模拟基于一个修正的混凝土单轴受压应力-应变关系,通过合理地选择单元模型和材料参数,可以比较准确地预测组合柱的力学性能.但是该应力-应变曲线并不连续,当遇到更加复杂的模型时可能会导致计算不收敛,此问题有待解决.与试验结果的比较表明,对于FRP约束混凝土柱在轴心受压作用下,该有限元模拟方法是可行的.
(2)通过将Teng分析模型和设计模型计算结果与数值模拟和试验结果进行比较,发现受约束混凝土轴向平均应力-应变曲线基本吻合,进一步验证了这两种理论模型的准确性和可靠性.
(3)根据已有有限元模型对各材料厚度变化时复合套管的约束性能进行模拟分析,结果表明当FRP管、钢管和混凝土厚度发生变化时,受约束的核心混凝土轴向平均应力-应变曲线表现出不一样的变化规律,为揭示复合套管的工作机理和相关理论研究提供了参考.
参考文献:
[1] Teng J-G, Yu T, Wong Y L,etal. Hybrid FRP-concrete-steel tubular columns:Concept and behavior [J]. Construction and Building Materials, 2007, 21(4):846-854.
[2]刘玉雷. GFRP管-混凝土-钢管混凝土组合柱轴压性能试验研究[D]. 大连:大连理工大学, 2014.
LIU Yu-lei. The experimental study on GFRP-concrete-steel-concrete double-skin tubular hybrid columns under axial compression [D]. Dalian:Dalian University of Technology, 2014. (in Chinese)
[3]Yu T, Teng J-G, Wong Y L,etal. Finite element modeling of confined concrete-I:Drucker-Prager type plasticity model [J]. Engineering Structures, 2010, 32(3):665-679.
[4]Yu T, Teng J-G, Wong Y L,etal. Finite element modeling of confined concrete-II:Plastic-damage model [J]. Engineering Structures, 2010, 32(3):680-691.
[5]陆新征,冯 鹏,叶列平. FRP布约束混凝土方柱轴心受压性能的有限元分析[J]. 土木工程学报, 2003, 36(2):46-51.
LU Xin-zheng, FENG Peng, YE Lie-ping. Behavior of FRP-confined concrete square columns under uniaxial loading [J]. China Civil Engineering Journal, 2003, 36(2):46-51. (in Chinese)
[6]余小伍. CFRP-混凝土-钢管组合柱轴压性能的研究[D]. 哈尔滨:哈尔滨工业大学, 2006.
YU Xiao-wu. Research on behaviors of hybrid CFRP-concrete-steel double-skin tubular columns [D]. Harbin:Harbin Institute of Technology, 2006. (in Chinese)
[7]韩林海. 钢管混凝土结构—理论与实践[M]. 2版. 北京:科学出版社, 2007.
HAN Lin-hai. Concrete-filled Steel Tubular Structures-Theory and Practice [M]. 2nd ed. Beijing:Science Press, 2007. ( in Chinese)
[8]何 政,欧进萍. 钢筋混凝土结构非线性分析[M]. 哈尔滨:哈尔滨工业大学出版社, 2006.
HE Zheng, OU Jin-ping. Nonlinear Analysis of Reinforced Concrete Structure [M]. Harbin:Harbin Institute of Technology Press, 2006. ( in Chinese)
[9]Dassault Systemes Simulia Corporation. ABAQUS/CAE User′s Manual-Theory Manual, Version 6.10 [Z]. Rhode Island:Dassault Systemes Simulia Corporation, 2010.
[10]Lee Jee-ho, Fenves G L. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechanics, ASCE, 1998, 124(8):892-900.
[11]Yu T, Teng J-G, Wong Y L. Stress-strain behavior of concrete in hybrid FRP-concrete-steel double-skin tubular columns [J]. Journal of Structural Engineering, ASCE, 2010, 136(4):379-389.
[12]Wong Y L, Yu T, Teng J-G,etal. Behavior of FRP-confined concrete in annular section columns [J]. Composites Part B-Engineering, 2008, 39(3):451-466.
[13]Teng J-G, Huang Y-L, Lam L,etal. Theoretical model for fiber-reinforced polymer-confined concrete [J]. Journal of Composites for Construction, 2007, 11(2):201-210.
[14]Teng J-G, Jiang T, Lam L,etal. Refinement of a design-oriented stress-strain model for FRP-confined concrete [J]. Journal of Composites for Construction, 2009, 13(4):269-278.
文章编号:1000-8608(2016)04-0375-07
收稿日期:2015-12-09;修回日期: 2016-05-28.
基金项目:国家自然科学基金资助项目(51378089).
作者简介:张俊林(1990-),男,硕士生,E-mail:vick_dut@163.com;任慧韬*(1973-),男,博士,副教授,E-mail:renht@dlut.edu.cn.
中图分类号:TU398.9
文献标识码:A
doi:10.7511/dllgxb201604008
Finite element analysis for confinement behavior of hybrid FRP tube-concrete-steel tube composite bushing
ZHANGJun-lin,RENHui-tao*,WANGSu-yan
( State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China )
Abstract:In order to study the confinement behavior of hybrid FRP tube-concrete-steel tube composite bushing, a finite element(FE) method is introduced to simulate FRP confined concrete short columns using ABAQUS software, and a modified Hognestad formula is presented to describe the stress-strain relations of concrete under uniaxial compression. The comparison of simulation and test results shows that this FE method does well in predicting mechanic properties of FRP confined concrete short columns by defining material parameters, element models, surface interactions and boundary conditions accurately. Based on these analytical data mentioned above, confinement behavior of FRP tube-concrete-steel tube composite bushing under three kinds of material thicknesses is analyzed. Study results indicate that the stress-strain curve of the concrete confined by the composite bushing presents a bilinear shape, in which the first line is decided by the steel tube mainly, while the second one by the FRP tube and concrete. Some references are provided for further research of this kind of composite column.
Key words:FRP; composite bushing; finite element method; stress-strain relations

