地下水溶质运移数值法和解析法预测结果对比分析——以沾化电厂为例

刘志涛，周群道，杨建华

(山东省鲁北地质工程勘察院，山东 德州　253072)



地下水溶质运移数值法和解析法预测结果对比分析
——以沾化电厂为例

刘志涛，周群道，杨建华

(山东省鲁北地质工程勘察院，山东 德州253072)

摘要：数值法和解析法是当前解决地下水流和溶质运移问题最常用的两种方法，虽然数值法以其广泛的适用性和较高的仿真性等优点取得了越来越普遍的应用，但解析法也以其简单易用等特点一直成为首选方法之一。该文以沾化电厂地下水环评项目为例，分别采用两种方法对污染物在长期和短期渗漏情况下对地下水所造成的污染情况进行了预测，并在对两种方法预测结果的差异进行分析的基础上，论述了解析法在该区的适宜性，为解析法在该区的应用提供了参考。

关键词：地下水；溶质运移；数值法；解析法

引文格式：刘志涛，周群道，杨建华.地下水溶质运移数值法和解析法预测结果对比分析——以沾化电厂为例[J].山东国土资源，2016,32(7)：78-82. LIU Zhitao, ZHOU Qundao, YANG Jianhua. Comparative Analysis on Prediction Results by Using Numerical Method and Analytical Method of Solute Transport in Groundwater——Taking Zhanhua Power Plant As an Example[J].Shandong Land and Resources, 2016,32(7)：78-82.

0引言

数值法和解析法是目前进行地下水水流运动和溶质运移预测最常用的方法，尤其是随着计算机科学技术的飞速发展，数值法在很多领域都得到了越来越广泛的应用，并使得许多过去难以解决的复杂地下水运动问题在一定程度上得到了解决，同时也提高了对相关领域的研究水平[1]。但建立地下水数值模型对水文地质资料的精度和深度要求比解析法要高很多，且由于模型识别验证需要一定的时间，使得项目持续时间较长。

在实际地下水环境影响评价工作中，由于各地水文地质工作的研究程度有着很大不同，同时受到项目周期、资金等因素的影响，解析法仍有着广泛的应用。该文以滨州沾化电厂为例，分别用数值法和解析法进行了溶质运移预测，并对预测结果进行了对比分析，以探索解析法在该区的适宜性。

1工作区水文地质特征

工作区处于滨州市沾化北部，属鲁西北平原松散岩类水文地质区、滨海冲积海积平原咸水水文地质亚区[2]，区域地层呈水平层状分布。区内地下水类型为第四系松散岩类孔隙水，按水力特征又分为浅层孔隙潜水-微承压水和中、深层承压水[3]，其中浅层地下水是该次工作主要研究对象。

(1)浅层潜水-微承压水。工作区内浅层潜水-微承压水全部为咸水，埋藏深度小于60m，含水层岩性主要是粉砂，共2～3层，累计厚度15m左右，单井涌水量200m3/d左右，富水性较差。地下水埋深1.5～4.3m，由南向北递增，年变化幅度一般在1.5m以内，地下水水位动态主要受气象因素的影响，水位动态曲线与大气降水的分配过程基本一致。地下水水质普遍较差，矿化度均大于10g/L，水化学类型以Cl-Na型为主。工作区地下水水位埋深较浅，以垂直方向的补给、排泄为主，大气降水为其主要补给源，蒸发式主要排泄途径。地下水流向自南向北，径流极为缓慢，水力梯度在0.6×10-3左右。

(2)中深层承压水。工作区内中深层承压水皆为咸水，埋深在60～200m范围内，含水层岩性主要为粉细砂，富水性差，单井涌水量一般小于500m3/d，水化学类型主要为Cl·SO4-Na型水，矿化度在19g/L左右。该含水层与浅层地下水之间存在较厚的粘土层，隔水性能相对较好，两含水层之间水力联系较弱。

(3)深层承压水。深层承压水顶板埋深一般在200m左右，含水层岩性多为粉细砂，富水性中等，单井涌水量500～1000m3/d，矿化度均大于3g/L，水化学类型多为氯化物-钠型。深层承压水埋藏深度较大，含水层层次多，累计厚度亦较大，与上部含水层之间存在以粘土为主的稳定隔水层。

工作区内，浅、中、深各含水层组之间普遍存在厚度较大、分布广泛、隔水性能相对较好的粉质粘土或粘土层，且各含水层的水质、水位有着明显差别，反映了浅、中、深3个含水层组之间地下水水力联系微弱[4]。

2数值法预测

2.1数值模型的建立

在平面上，模拟区范围主要根据工作区水文地质条件并结合地下水流场确定，东部边界与等水位线基本垂直，南、北部边界与等水位线大致水平，西部以河流为界，面积约90km2(图1)。在垂向上，该次模型概化为两层。第一层主要岩性为粉土、粉质粘土，底界面埋深3.4～5.5m，第二层以粉砂为主，底界面埋深19.4～24.5m，是主要含水层。第二层以下有累计厚度超过15m的粉质粘土层，其垂向渗透系数在(1.27～8.11)×10-8cm/s之间，具有良好的隔水性能，因此将其概化为模型的不透水底部边界。垂向上水量交换主要为大气降水入渗补给和潜水蒸发排泄。

图1　模拟区范围图

地下水水流模型采用非稳定三维渗流数学模型[5-6]，具体可以描述为：

式中：H—水头；K—渗透系数；Ss—贮水率；W—源汇项；G—研究域；Γ—研究域的边界。

溶质运移模型采用不考虑吸附、挥发以及生物化学反应情况下的三维非稳定流数学模型[7-8]，具体可以描述为：

式中：C为浓度；Dij为水动力弥散系数张量的分量；W为源汇项；Cw为随W注入的污染物浓度；Rd为滞留因子；n为孔隙度；ui为水流实际速度分量；其他符号同前。

模拟软件采用Visaul Modflow 4.2，水文地质参数主要根据该次工作野外试验以及以往该区所开展的地质勘查成果初步确定，然后通过拟合流场进行调参，调整后的参数取值见表1。由于模型建立、识别和验证不是该文的主要研究对象，这里不再对其过程进行详细论述。

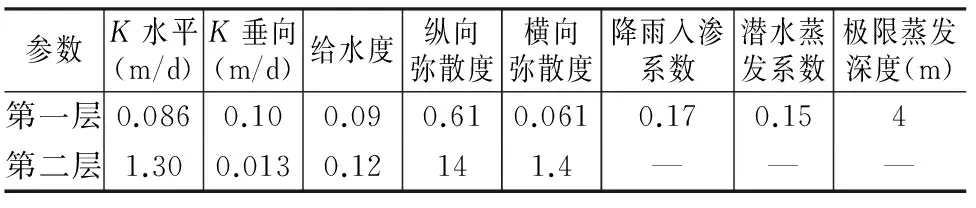
表1　水文地质参数取值

2.2地下水污染预测情景设定

项目污染源多种多样，但根据污染源渗漏情况，一般可分为长期渗漏和短期渗漏，该文分别选择一种情况进行预测。

(1)长期渗漏。该次对厂区污水处理站池底出现裂缝，使得污水发生长期微量渗漏的情况进行预测。假定池底出现长5m，宽5cm的裂缝，根据包气带土层渗透系数计算得通过裂缝渗漏的污水量为0.06m3/d。特征污染物为COD，浓度为200mg/L。

(2)短期渗漏。该次对柴油储罐发生爆炸破坏地面防渗层，导致石油类污染物短期渗漏的情况进行预测。假定爆炸破坏地表防渗结构面积为25m2，事故发生后污染物24小时清理完毕，同样根据包气带土层渗透系数计算得通过破坏层的污染物体积为5.86m3/d。特征污染物为轻柴油(石油类)，浓度为6800mg/L。

2.3预测结果

该次模拟，当预测点浓度大于相应污染物的标准浓度时视为超标，标准浓度根据《地下水质量标准》(GB/T14848-93)中的三类标准或《生活饮用水卫生标准》(GB5749-2006)确定，COD和石油类分别为3.0mg/L和0.3mg/L。当模拟浓度小于于相应污染物的检出限时，视为对地下水无影响，COD和石油类对应的检出限分别为0.1mg/L和0.005mg/L。根据模拟预测结果，在1年末、5年末、10年末其超标范围、影响范围、最大运移距离见表2和图2。

3解析法预测

3.1污染物迁移解析解

同样对长期渗漏和短期渗漏两种情况进行预测，污染场景假设同前。

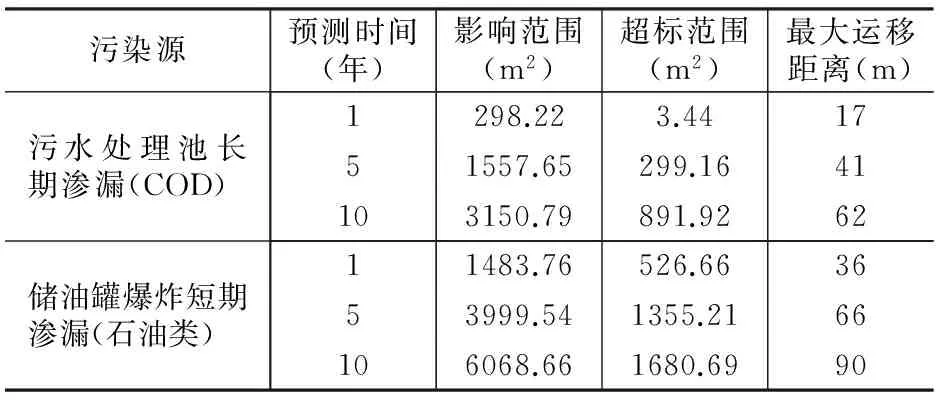
表2　地下水污染数值法预测结果

图2　地下水污染数值法预测结果图(10年末)

(1)点源定通量连续注入污染物二维迁移问题解析解。假设含水层在x，y平面上无限分布且含水层介质均质各向同性，有点源污染物在含水层厚度上连续定质量注入，地下水沿x方向均匀等速流动，不考虑吸附解吸和化学反应作用[9-10]，其解析解为：

(2)点源瞬时注入污染物二维迁移问题的解析解。假设含水层在x，y平面上无限分布且含水层介质均质各向同性，初始时刻在整个含水层厚度上瞬时注入一定量的污染物，地下水沿x方向均匀等速流动，不考虑吸附解吸和化学反应作用，其解析解为：

式中：m为瞬时注入污染物质量；其他符号同前。

3.2预测结果

各参数取值与数值法相同，另外地下水流速按u=k·I/n计算，水力梯度I根据枯、丰水期等水位线图确定，最终计算得渗漏点处水流速度约为5.38×10-3m/d。预测结果见表3和图3。

表3　地下水污染解析法预测结果

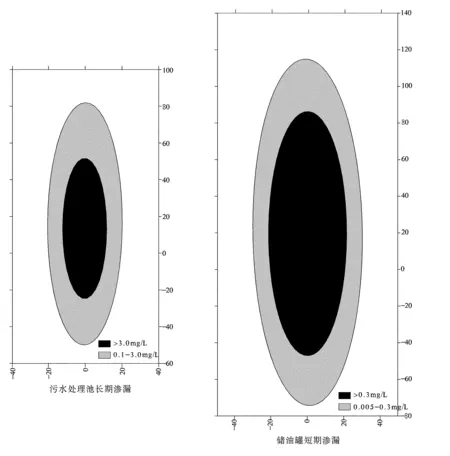
图3　地下水污染解析法预测结果图(10年末)

4不同预测方法的预测结果分析

根据预测结果，对于解析法，污染物超标范围和影响范围呈规则的椭圆形，而数值法则呈不规则椭圆形，主要是因为解析法中假定地下水为均匀稳定流，而数值法中地下水流场基本符合地下水的实际运动特征。通过对两种预测方法影响范围和超标范围面积的比较，数值法均小于解析法，主要是由于数值法模拟了污染物从地面下渗到含水层中然后再不断扩散这一整个过程，而解析法中则假定污染物直接在含水层中注入，不考虑下渗过程，也就是说在垂向上，深度越大，数值法对污染面积的预测结果越小，而解析法预测结果不随深度变化。

两种方法对最大运移距离的预测结果较为接近，主要是因为工作区水力梯度很小且变化不大，使得地下水径流缓慢且较稳定，含水层单一且厚度也相对较稳定，另外包气带厚度较薄，下渗过程对预测结果的影响较小。但如果条件改变，利用解析法求解时就必须考虑这些影响因素，否则预测结果将与实际差别较大，比如当包气带厚度较大或垂向渗透性较差时，污染物下渗至含水层的时间可能较长，若不考虑下渗过程，则最大运移距离预测结果可能要大很多，尤其是当地下水流速较大时；另外，在多含水层系统且水力联系较密切时，含水层厚度的确定也应考虑下渗过程，根据预测时段内可能影响到的深度确定，否则对预测结果的影响很大。

由于解析法引入了更多的各种假定，使得与地下水真实状态相差较大，而数值法则能较好地根据实际调查资料建立模型，更为接近地下水实际特征，因此从其理论基础上来讲，数值法预测结果要优于解析法。虽然解析法对影响面积和超标范围的预测结果和数值法相比有一定的差异，但未造成质的影响，比如对于储油罐渗漏情况下，数值模拟法所预测的椭圆形影响范围的长轴和短轴分别为148m和57m，解析法则为182m和58m，相差并不是很大，两种方法对最大运移距离的预测结果很接近，因此在该区采用解析法是适宜的，以其预测结果作为污染物防治的依据也是完全可行的。

5结论

从理论基础上讲，数值模拟法预测结果优于解析法。通过对本例数值法和解析法预测结果的对比分析，其最大距离预测结果较为接近，影响面积和超标范围的预测结果虽有一定的差异，但未对结果造成质的影响，据此作为地下水污染防治的依据也是完全可行的。在对造成预测结果差异的原因进行分析的基础上，认为在鲁北平原区，水文地质条件相对简单，同一地段地层分布相对较稳定，包气带厚度一般较小，可忽略污染物下渗过程，地下水径流缓慢且较稳定，在此条件下采用解析法是适宜的。

参考文献：

[1]沈媛媛，蒋云钟，雷晓辉等.地下水数值模型在中国的应用现状及发展趋势[J].中国水利水电科学研究院学报，2009，7(1):57-58.

[2]康凤新，徐军祥，张中祥.山东省地下水资源及其潜力评价[J].山东国土资源，2010，26(8):4-6.

[3]刘桂仪.鲁北平原深层地下水基本特征与水环境问题[J].山东国土资源，2001，17(5):43-44.

[4]张中祥，罗斐，张海林.鲁西北平原深层地下水动力场时空演化[J].山东国土资源，2011，27(10):32-33.

[5]郭东屏.地下水动力学[M].陕西：陕西科学技术出版社，1994：62-87.

[6]郭东屏，张石峰.渗流理论基础[M].陕西：陕西科学技术出版社，1994：27-32.

[7]薛禹群，谢春红.地下水数值模拟[M].北京：科学出版社，2007：18-28.

[8]孙讷正.地下水污染-数值模型和数值方法[M].北京：地质出版社，1989：10-18.

[9]王洪涛.多孔介质污染物迁移动力学[M].北京：高等教育出版社，2008：246-253.

[10]陈崇希，李国敏.地下水溶质运移理论及模型[M].北京：中国地质大学出版社，1995：95-102.

收稿日期：2015-09-12；

修订日期：2015-11-19；编辑：曹丽丽

作者简介：刘志涛(1982—)，男，河南巩义人，工程师，主要从事水工环地质工作；E-mail：strawer@126.com

中图分类号：X523

文献标识码：B

Comparative Analysis on Prediction Results by Using Numerical Method and Analytical Method of Solute Transport in Groundwater——Taking Zhanhua Power Plant As an Example

LIU Zhitao, ZHOU Qundao, YANG Jianhua

(Lubei Geo-engineering Exploration Institute,Shandong Dezhou 253072, China)

Abstract:At present, numerical method and analytical method are the methods most commonly used for solving groundwater problems. Although numerical method has been widely used for its wide applicability and higher simulation, the analytical method has been one of the first choice for its simple and easy to use. Taking Zhanhua power plant as an example, the pollution caused by long-term and short-term leakage of pollutants have been predicated in this paper. The application suitability of the analytical method in the study area has been discussed based on analyzing the differences between the predictions results gained by using two methods. It will provide reference for the application of this method.

Key words:Groundwater；solute transport；numerical method；analytical method