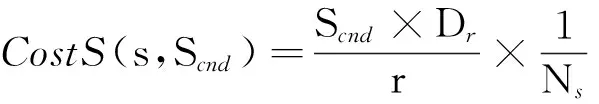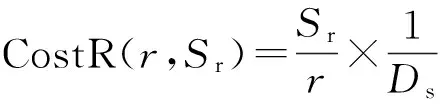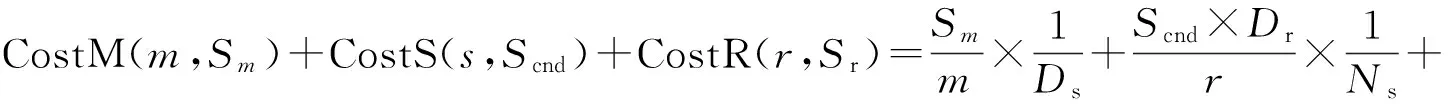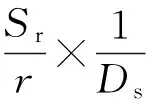移动云计算环境下的双色反近邻查询算法

季长清,余　胜,王宝凤,陶　帅,汪祖民,王润方

(1. 大连大学 物理科学与技术学院,辽宁 大连 116622；2. 大连大学 信息工程学院,辽宁 大连 116622)



移动云计算环境下的双色反近邻查询算法

季长清1,2,余胜1,王宝凤2,陶帅2,汪祖民2,王润方2

(1. 大连大学 物理科学与技术学院,辽宁 大连 116622；2. 大连大学 信息工程学院,辽宁 大连 116622)

摘要:研究在移动云计算环境下的最大双色反最近邻查询优化问题,设计新的高效的双色反最近邻查询算法——SILM算法.SILM算法是基于MapReduce框架下的倒排网格索引结构,在Map函数中对分片数据区域使用 PCT 轮圈算法.对包含在圆区域内或与圆相交的网格的权值记为1,在Reduce函数中使用网格处理算法对分片数据区域进行扫描及合并,对重叠的网格的权值进行累加,输出网格空间中权值最大的网格区域.SILM算法可以在多计算节点上进行分布式计算,更适合于在移动云计算环境下处理大规模并行查询请求.通过实验对SILM算法的效率进行验证.实验结果表明,当数据量较大(数据点个数大于2.0×106)时,SILM算法的查询效率是目前解决最优选址问题最佳算法的2倍.

关键词：最大双色反最近邻查询；倒排网格索引；移动云计算

近年来，随着移动定位技术(mobilepositioningtechnology,MPT)和地理信息系统(geographicinformationsystem,GIS)等技术的发展，空间数据查询技术受到学术界的广泛关注.反最近邻(reversenearestneighbor,RNN)查询[1-5]作为空间数据查询技术中最重要的查询技术之一，学术界对该查询技术展开了深入研究，已提出了多种用于解决RNN查询问题、双色反最近邻(bichromaticreversenearestneighbor,BRNN)查询[6-8]问题和最大双色反最近邻(maxbichromaticreversenearestneighbor,MaxBRNN)查询[9-10]问题的算法，但这些算法无法解决在移动云计算环境下难以并行运行，从而导致查询效率低下的问题.

目前，MaxOverlap算法[11]是解决最优选址问题的最佳算法，该算法通过求解多个最近位置圆(nearestlocationcircle,NLC)的交点解决MaxBRNN问题.其中，NLC是以客户c的位置为圆心，以客户c与该客户最近邻的距离为半径的圆.

MaxOverlap算法是第一个通过多项式时间求解MaxBRNN问题的算法，该算法的时间复杂度O(|O|log|P|+m2|O|+m|O|log|O|)为二阶多项式(其中m为NLC相交次数的最大值).随着NLC交点的增多,采用MaxOverlap算法求得最优位置区域的效率急剧下降,该缺点在大数据环境下尤为明显.

MaxOverlap算法采用的R-tree索引结构因传统的自上而下和层次遍历搜索特性,导致该算法很难在移动云计算环境下直接运行.而复杂的结构和固有的顺序执行等特性使得该算法不支持并行运行.所以,MaxOverlap算法在大数据情况下存在查询等待时间过长的问题.

而很多实际问题(如地震救灾服务点的设置、战机群的空中最佳加油点等)都需要在较短的时间内得到最优位置区域,因此需要设计响应时间短的算法高效地求解MaxBRNN问题.本文通过对RNN查询、BRNN查询等问题及相关算法的研究,设计了能够高效解决MaxBRNN问题的ScalableInfluentialLocationMiner算法(简称SILM算法).

1相关工作

近年来,RNN查询研究最初是从暴力地线性扫描全部空间对象开始的[4],后来经过不断的技术改进与算法优化[1-5,12-13],RNN查询研究日益成熟.目前,有效的索引与查询是RNN查询研究的两个密切相关的问题.在索引方面,基于R-tree索引的RNN查询如KM[4]与YL[12],采用的层次结构化方法不适合在分布式环境下运行；增量的IGERN[6]采用网格索引,但只能监控较小的数据集,上述索引方法目前只在非分布式环境下被证明是正确的.在查询方面,Singh等[3]提出的近似算法SFT存在查询结果丢失的问题；TPL算法[1]是目前单机环境下最好的RNN查询算法之一,由于大量的迭代过程及R-tree结构,采用该算法很难进行分布式处理.现有的RNN查询算法研究因索引、查询的结构化特性等问题,导致算法存在潜在的顺序执行、缺乏精度、产生维灾难以及不能在移动云计算环境下运行等问题.因此,关于RNN查询的研究仍面临困难与挑战.

随着基于位置的服务(locationbasedservice,LBS)相关研究与应用的兴起,新的支持各类大规模RNN查询算法相继被开发,但能够有效地支持大规模RNN查询的研究成果较少.在已有的研究中,MRVoronoi算法[13]除设计空间索引结构外,也简略地描述了利用MapReduce[2]框架进行RNN查询的过程,但该算法需要额外时间定位查询点,当维度增加时需要较高的维护与计算代价.RankReduce算法[5]通过利用MapReduce框架处理大规模近似kNN查询问题,但该算法不精确,只适用于高维条件,且没有描述解决RNN查询的过程.现有的方法均不能很好地直接用来解决大规模RNN查询问题.

基于RNN查询研究存在的问题,Kang等[6]开发了BRNN查询算法,该算法在空间数据库中已得到广泛应用,一直被用来在众多服务点中查找“最有影响力”的服务点.在已有的研究中,MaxOverlap算法[11]通过计算查询集与数据集中点之间的NLC交点求解MaxBRNN问题；Liu等[14]基于MaxOverlap算法提出MaxSegment算法解决MaxBRNN问题,该算法将MaxBRNN问题转变为最优圆弧搜索问题；FILM算法[15]是一种基于网格的近似算法,该算法可以保证返回的小网格单元对所有位置区域都有影响.

由于单机环境下的计算与存储能力有限,无法支持大规模空间查询,最好的解决方案是同时利用多个计算节点并行参与分布式计算并提高计算效率,因此需要设计新的分布式索引与并行查询算法.2004年,Google提出的MapReduce框架[2]可以在云计算环境下并行执行Map和Reduce阶段支持大规模并行数据分析.基于此,本文提出SILM算法,该算法在倒排网格索引结构的基础上设计双色反最近邻查询算法.SILM算法能够在移动云计算环境下运行,可以提高求解大规模MaxBRNN问题的计算效率.本文首先利用SILM算法对空间数据集进行离线预计算,然后在在线实时查询时直接推送结果,从而实现SILM算法在移动云计算环境下的高效实时运行效果.

2问题定义

定义1最近邻(nearestneighbor,NN)查询[16]给定空间数据集P和一空间点p,dist(p,pi)为p和pi之间的距离,最近邻查询是求P中的一个子集NN(p),其中NN(p)满足表达式：

NN(p)={pi∈P|∀pj∈P:

dist (p,pi)≤dist (p,pj)}.

定义2k近邻(knearestneighbor,kNN)查询[5]给定一个查询点c,kNN查询找到k个到查询点c的最近数据点si∈S,其中dist(c,si)≤dist(c,s).其中,si∈S为kNN查询结果集,s∈S为kNN查询结果集以外的点.

定义3反最近邻(reversenearestneighbor,RNN)查询[11]假设D维数据集P和查询点q,RNN查询是找出P的子集RNN(q),满足RNN(q)={pi∈P|∀pi∈P:dist(q,pi)≤dist(pi,pj)},i≠j.

其中,dist( )为对象间的欧氏距离,pj∈P为q的k近邻,k=1时为RNN查询,k≥2时为RkNN查询.

定义4双色反最近邻(bichromaticreversenearestneighbor,BRNN)查询[11]给定欧氏距离空间数据集P和O,其中P和O是不同类型的数据集,若给定数据集P中的一点p,双色反最近邻查询结果是返回所有点o∈O,其中o是p∈P的反最近邻,即不存在任意一点p′∈P满足dist(o,p′)

如图1所示,给定便利店集合S和顾客集合C,假设数据集中有2个便利店S1、S2及5个顾客C1、C2、C3、C4和C5的位置信息,若顾客总访问距离最近的便利店,则顾客C1、C2、C3总访问便利店S1,顾客C4和C5总访问便利店S2.对于BRNN查询有BRNN(S1, S) = {C1, C2, C3}和BRNN(S2, S) = {C4, C5},若想开设一家新的便利店S3,则需要找到一个最优位置区域,使得S3被安置在该区域时能够吸引尽可能多的顾客,那么如何得到满足该条件的最优位置区域呢？这是一个简单的BRNN查询问题.

定义5最近位置圆(nearestlocationcircle,NLC)[11]给定客户对象c∈C,NLC是以客户c的位置为圆心,半径为d(c,NN(c,S))的圆,其中NN(c,S)是客户c的最近邻.如图1所示,客户c1的NLC是以c1为圆心,半径为d(c1,NN(c1,S))的圆,客户c2的NLC是以c2为圆心,半径为d(c2,NN(c2,S))的圆.

定义6最大双色反最近邻(maxbichromaticreversenearestneighbor,MaxBRNN)查询[11]假设存在查询集P和数据集O.MaxBRNN查询需要返回最大区域R,R满足下面条件：若新服务点p建立在R中,则p点对整个区域的影响最大.若查询集P和数据集O的数据个数均为2,MaxBRNN查询返回的最大区域R为图1的阴影区域A.

定义7 倒排网格索引(invertedgridindex,IGI)结构 在大规模空间数据集中,倒排网格索引结构是用来存储网格空间中网格(Cell)的划分与空间数据对象间倒排映射关系的一种空间数据索引结构.

图1　最近位置圆示例Fig.1　Example of nearest location circle

3SILM算法

MaxOverlap算法[11]是目前解决最优选址问题的最佳算法.该算法通过在查询集与数据集中的点之间绘制NLC求解MaxBRNN问题,通过找到NLC间重叠最多的部分,得到最好的双色反近邻查询结果区域.如图2所示,客户集合C = {c1, c2, c3, c4, c5}和便利店集合S = {s1, s2},MaxOverlap算法通过绘制NLC以及求解大量的NLC交点获得最佳位置区域(见图2(d)的阴影部分).

图2　MaxOverlap算法示例[11]Fig.2　Example of MaxOverlap algorithm[11]

MaxOverlap算法需要计算和评估多个NLC交点,所以该算法的时间复杂度为二次方,执行效率较差.此外,MaxOverlap算法是在单机环境下设计的串行算法,不支持分布式并行分解,所以该算法不能在移动云计算环境下直接运行.针对MaxOverlap算法存在的缺点,开发SILM算法进行改进.

图3　SILM算法的Map函数Fig.3　Map function of SILM algorithm

首先,建立空间网格索引,并整体扫描网格空间,从而得到IGI数据结构.然后在Map函数中对分片数据区域使用PCT轮圈算法[17],如图3所示,即以点ci为圆心,r = |ci, si|为半径轮圈,同时将圆区域内或与圆相交的网格Counter(gi)值记为1,即Counter(gi)=1,其中gi为网格被一个节点遍历过的次数.如图3所示为以c1、c2为圆心,以d(c1, s1)、d(c2, s2)为半径的轮圈结果.若网格被扫描2次,Counter(gi) = 2；若网格被扫描3次,Counter(gi) = 3,以此类推.

每个分片数据区域单独处理后,在Reduce函数中按照网格处理算法扫描及合并,在每次扫描的过程中,采用类似于文献[18]的WordCount算法对重叠的网格Counter(gi)值累加,最后输出整个空间区域权值W最大的网格区域.如图4所示为两个NLC重叠的执行过程与结果,其中深色阴影部分为两个NLC合并后的最终输出结果.

图4　SILM算法的Reduce函数Fig.4　Reduce function of SILM algorithm

具体的SILM算法伪码如算法1所示.

算法1SILM

输入:InvertedgridindexG,DatasetC, S, ci∈C, si∈S

输出:SILM(C, S)∥theSILMCells

Map( ):

1.InitializesetScnd=PCT(G, si, k)

2.foreachPCTRounddo

3.Counter(g0)=0

4.fori=1ton

5.ifCellisscanned

6.emit(Counter(gi)) =Counter(gi-1)+1

7.endif

9.endfor

Reduce( ):

10.Counter(gi)=0

11.foreachvalueinvaluesdo

12.Counter(gi) =Counter(gi)+value;

13.endfor

14.emitcellofmax(Counter(gi))

3. 《陆游年谱》(于北山著)，绍兴二十八年(1158)：“七月，曾幾为礼部侍郎，有贺启。八月，王师心来为绍兴守，对务观颇加礼遇，陈棠由山阴应召赴临安，赋诗送之，……。冬季，始出仕，为福州宁德县主簿。”⑤

该算法的执行步骤如下.

1)扫描整个网格空间中的数据并建立IGI.IGI数据结构中包含存储在每个网格单元内的空间对象列表.在空间查询时,首先要确定网格空间中网格的位置,然后查找该网格内的所有空间对象.

如图5所示为4×4倒排网格索引示例,网格C1指向包含(P2、P1、P3)的空间对象数据列表.可采用预聚类索引方法改良网格索引的数据倾斜问题.为了节约篇幅,这里不再复述,详见文献[19].

如图6所示为基于预聚类的倒排网格索引示例,包含4×4网格,以Key-Value值存储数据,如集合CS1,包含和.基于预聚类的倒排网格索引的实验分析,详见文献[19].

图5　倒排网格索引示例Fig.5　Example of inverted grid index

图6　基于预聚类的倒排网格索引Fig.6　Pre-clustering based inverted grid index

2)在索引的基础上,在Map函数中对网格进行分区.

Map函数：每个Mapper并行读取一个文件分块,给定一个客户对象c∈C,采用CellCount方法轮次访问网格周围的对象c.若s∈S的数量超过k,Map将客户对象作为Key值并给出其在S中的值.

3)分区后对每一个节点进行单独处理,利用kNN轮圈方法画圆求得kNN查询结果集(算法1的第1行).

图7　kNN轮圈示例Fig.7　Example of kNN Round

kNN轮圈的目的是在空间数据集P中找到距离查询点q最近的k个点.如图7所示为以q为圆心,分别以与q相距最近的k个点为半径轮圈,直至找到k个点为止.若k取1,则kNN为NN.NN查询为在数据集P中找到距离查询点q的最近点.

4)利用遍历算法对网格计数,遍历一次的网格Counter(gi) = 1,遍历两次的网格Counter(gi) = 2,遍历三次的网格Counter(gi) = 3,依次类推,直至kNN查询结果集中的所有数据点均被遍历为止(算法1的第3～8行).

PCT算法的基本思想是以查询点q为圆心,一轮轮并行读取周围的网格.如图8(a)所示为第一批轮圈组,包括半径为δ和2δ的两个轮圈线程并行执行CircleTrip算法求NN.如图8(b)所示为批量并行执行半径为3δ和4δ的轮圈.

图8　PCT算法示例Fig.8　Example of PCT algorithm

5)在Reduce函数中扫描及合并.在扫描过程中,对重叠的网格Counter(gi)值累加(算法1的第11～13行),最后输出数值最大的网格区域作为查询结果(算法1的第14行).

Reduce函数：Reducer将在Mapper中获得的查询点或查询点集作为Key值,NN查询对象点作为Value值.通过欧氏距离计算得到查询点q与近邻点的距离,排序得到kNN结果集,并作为Reduce函数的最终输出结果.

4BRNN算法的分析比较

4.1时间复杂度

MaxOverlap算法的时间复杂度O(|O|×log|P|+m2|O|+m|O|log|O|)为二阶多项式(其中m为NLC相交次数的最大值).

对于SILM算法,需要构造服务点网格索引,该步骤的时间复杂度为O(|S|log|S|),从Ji等[20]的工作可知,网格索引的性能明显优于R-tree索引.使用网格对NLC进行计算并通过访问最小数量的网格发出轮圈遍历NN查询结果,该步骤的时间复杂度为O(|C|log|S|).对于每次遍历的n个网格,使用CellCount算法计算网格的最大值,该步骤的时间复杂度为nO(l).SILM算法的时间复杂度O(|S|×log|S|+|C|log|S|+nO(1))为一阶多项式.SILM算法的时间复杂度明显低于MaxOverlap算法.

4.2代价模型

SILM算法与之前的工作相比,因采用倒排网格索引结构与并行查询方法,更适合在移动云计算环境下运行.在MapReduce框架下,从3个阶段分析SILM算法的时间代价.

1)Map阶段.m个Mappers处理Sm字节的数据,每个Mapper在本地磁盘处理数据的平均速率为Ds字节/s,则Map阶段的时间代价为

(1)

2)Shuffling阶段.Ss字节数据从Mapper经过洗牌传输到r个Reducers.洗牌的主要代价与网络在不同节点间的传输损耗有关.Dr为在不同的节点间实际传输的数据与所有数据的比率.在Shuffling过程中,传输的数据量为Scnd×Dr字节,这些数据被r个Reducers并行接收,每个Reducer的平均接收速率为Ns字节/s.Shuffling阶段的总时间代价为

(2)

3)Reduce阶段.r个Reducers处理Sr字节的数据,每个Reducer在本地磁盘读取数据的平均速率为Ds字节/s,则Reduce阶段的时间代价为

(3)

SILM算法的预期总时间代价为

(4)

由式(4)可知,SILM算法的效率受m、Ds、r等参数的影响.随着集群点数量的增加,SILM算法因采用MapReduce并行框架,总响应时间随数据点数量近似线性上升,而MaxOverlap算法因需要求解大量NLC交点,总响应时间随数据点数量近似二次方上升.

此处的Sm字节被并行读取,每个Mapper平均读取的字节为Sm/m,数据划分采用MapReduce框架下的随机划分机制,读取机制在MapReduce框架下自动进行,随机划分的正确性在文献[20]中已得到充分证明.

5实验研究

5.1实验设置

该实验集群为高速千兆以太网下由12个计算节点组成的服务器集群,其中1个16核AMD皓龙62 722.1GHz处理器为主节点,其他11个双核AMD2.0GHz处理器为从节点,每个节点都有SATA硬盘(300GB)、内存(64GB)和Ubuntu12.10服务器操作系统(64位).

对于所有实验设置相同的实验环境,在MaxReduce框架下,ClouderaHadoop2.0.0-cdh4.2.1的源码是在JDK1.7下编译的.主节点单独运行一个NameNode和JobTracker守护进程,从节点分别运行一个TaskTracker和DataNode守护进程.每个文件的复制因子均被设置为1,目的是避免写入开销以及在Mappers和Reducers之间传送的数据被压缩.每个Map过程和Reduce过程的虚拟内存为4GB,分布式文件系统块的大小为64MB.

该实验采用2个数据集：真实数据集(realdatasets,RDS)和仿真数据集(syntheticdatasets,SDS).RDS由美国东北部的企业信息(金融机构、汽车服务、餐馆和商店等)组成,该数据集从Navteq*http:∥www.navteq.com/.中检索得到,含约1.3×109个数据点,原始数据在解压前约为13GB.SDS为随机位置生成器在105×105空间域中产生,该数据集具有Zipf分布及偏度系数为0.2等特点,含约2.0×109个数据点,用以模拟真实世界.

5.2网格宽度影响

考虑到网格宽度δ会影响SILM算法的性能,采用学术界的通用方式,即通过多次训练性实验得到δ对SILM算法性能的影响,并确定使用2个数据集的最佳网格宽度.

通过对Ji等[17]的研究可知,在特定数据集中,网格宽度的最佳值取决于数据点分布.首先研究单机环境下δ的变化对CPU开销的影响,通过使用1.8×105个数据点的子集确定δ对CPU开销的影响.

如图9所示,网格宽度过大或过小都会导致SILM算法的性能降低.图中，T为算法执行时间.当δ较小(如δ为8×8)时,每个网格单元包含大量数据点,因此在每个网格中执行SILM算法时会消耗大量时间.当δ较大(如δ为256×256)时,每个网格单元包含少量数据点,虽然局部的计算时间较少,但网络和磁盘在移动云计算环境下运行会产生I/O开销.为了使SILM算法达到最佳性能,在密集的RDS中设置的网格宽度为64×64(见图9(a)),在稀疏的SDS中设置的网格宽度为128×128(见图9(b)).

图9　网格宽度对CPU开销的影响Fig.9　CPU overload under different grid widths

5.3数据点数量的影响

给出不同数量数据点下,MaxOverlap算法和SILM算法的平均响应时间T.图10给出在RDS和SDS中数据点数量n对T的影响曲线,复制因子n和k默认为1.图中,RDS中n从103变化到108,SDS中n从2.0×103变化到2.0×108.

如图10(a)所示,当n较小(104以下)时,MaxOverlap算法的性能优于SILM算法,这是由于SILM算法采用倒排网格索引交易空间换取时间所导致的.随着n的增加(104以上),由于MaxOverlap算法的响应时间T近似二次方上升,响应时间随着NLC交点的增加而迅速增加.SILM算法所采用的倒排网格索引结构解决NLC交点问题仅需要花费O(l)时间.随着n的增加,SILM算法响应时间T近似线性上升,因此,SILM算法较MaxOverlap算法花费的时间更少.如图10(b)所示,当n超过2.0×106时,MaxOverlap算法的响应时间T是SILM算法的2倍多.

图10　数据点数量对响应时间的影响Fig.10　Response time under different number of data points

图11　SILM算法的可扩展性Fig.11　Scalability of SILM algorithm

随着n的增加,SILM算法的效率较当前解决MaxBRNN问题最佳的MaxOverlap算法更高.

5.4SILM算法的可扩展性

研究SILM算法在RDS和SDS中的可扩展性.在MapReduce框架下,确定了最佳网格宽度并集中研究可扩展性的影响参数,其他参数如Mappers数值m、Reducers数值r等在集群资源中被自动确定.

研究服务点数量对SILM算法性能的影响,并将此影响命名为SS-SILM.将顾客数量固定为106,同时将服务点数量从104变化到108.研究顾客数量对SILM算法性能的影响,将此影响命名为CO-SILM,并将服务点数量固定为106,同时将顾客数量从104变化到108.如图11所示分别为SILM算法在RDS和SDS中的可扩展性.图中，N为参与计算的服务器节点数量.

如图11所示,随着N的增加及SILM算法的并行化扩大,SILM算法的两种影响的响应时间都近似线性减小.由图11可知,SS-SILM的性能优于CO-SILM,同时在RDS中,SS-SILM的响应时间比CO-SILM快了近0.3倍.这是由于SILM算法采用倒排网格索引结构,与顾客数量相比,服务点数量对NLC重叠的平均数量有更大的影响.

6结语

本文通过对MaxBRNN改良问题的研究,提出可以在移动云计算环境下快速查询的算法—SILM算法.该算法在倒排网格索引结构的基础上,设计了双色反最近邻查询算法.目前,最佳的MaxOverlap算法的时间复杂度为二阶多项式,而本文设计的SILM算法将时间复杂度降为一阶多项式,使得查询效率明显提高.实验结果表明,在移动云计算环境下,当数据点较大(数据点数量大于2.0×106)时,SILM算法的效率是MaxOverlap算法的2倍,这证明了SILM算法的高效性.

在今后工作中,将对SILM算法进一步优化,如结合Spark来采用更大规模的数据集进行实验,或采用类似于MapReduce的内存计算框架来进一步提高SILM算法的性能.

参考文献(References):

[1]TAOYu-fei,PAPADIASD,LIANXiang.ReversekNNsearchinarbitrarydimensionality[C]∥Proceedingsofthe30thInternationalConferenceonVeryLargeDataBases-Volume30.Toronto:VLDBEndowment, 2004: 744-755．

[2]DEANJ,GHEMAWATS.MapReduce:simplifieddataprocessingonlargeclusters[J].CommunicationsoftheACM, 2008, 51(1): 107-113．

[3]SINGHA,GLUHF,ALISAT.Highdimensionalreversenearestneighborqueries[C]∥Proceedingsofthe12thInternationalConferenceonInformationandKnowledgeManagement.NewYork:ACM, 2003: 91-98．

[4]KORNF,MUTHUKRISHNANS.Influencesetsbasedonreversenearestneighborqueries[C]∥ACMSIGMODRecord.NewYork:ACM, 2000: 201-212．

[5]STUPARA,MICHELS,SCHENKELR.RankReduce-processingK-nearestneighborqueriesontopofMapReduce[C]∥Proceedingsofthe8thWorkshoponLarge-ScaleDistributedSystemsforInformationRetrieval.Geneva:ACM, 2010: 13-18．

[6]KANGJM,MOKBELMF,SHEKHARS,etal.Continuousevaluationofmonochromaticandbichromaticreversenearestneighbors[C]∥23rdInternationalConferenceonDataEngineering.Istanbul:IEEE, 2007: 806-815．

[7]CONDIET,CONWAYN,ALVAROP,etal.MapReduceonline[C]∥ProceedingsofNSDI.SanJose:ACM, 2010, 10(4): 20．

[8]CONDIET,CONWAYN,ALVAROP,etal.OnlineaggregationandcontinuousquerysupportinMapReduce[C]∥Proceedingsofthe2010ACMSIGMODInternationalConferenceonManagementofData.NewYork:ACM, 2010: 1115-1118．

[9]LIUTing,ROSENBERGC,ROWLEYHA.Clusteringbillionsofimageswithlargescalenearestneighborsearch[C]∥IEEEWorkshoponApplicationsofComputerVision.AustinTexas:IEEE, 2007: 28．

[10]LIJun,ZHANGPeng,TANJian-long,etal.Continuousdatastreamqueryinthecloud[C]∥Proceedingsofthe20thACMInternationalConferenceonInformationandKnowledgeManagement.NewYork:ACM, 2011: 2389-2392．

[11]WONGRCW,TAMERÖZSUM,YUPS,etal.Efficientmethodformaximizingbichromaticreversenearestneighbor[J].ProceedingsoftheVLDBEndowment, 2009, 2(1): 1126-1137．

[12]YANGCong-Jun,LINKI.Anindexstructureforefficientreversenearestneighborqueries[C]∥Proceedingsof17thInternationalConferenceonDataEngineering.Heidelberg:IEEE, 2001: 485-492．

[13]AKDOGANA,DEMIRYUREKU,BANAEI-KASHANIF,etal.Voronoi-basedgeospatialqueryprocessingwithMapReduce[C]∥2010IEEE2ndInternationalConferenceonCloudComputingTechnologyandScience(CloudCom).Indianapolis:IEEE, 2010: 9-16．

[14]LIUYu-bao,WONGRC-H,WANGKe,etal.AnewapproachformaximizingbichromaticreversenearestneighborsearchKAIS-newapproachforMaxBRNN[J].KnowledgeandInformationSystems, 2012, 36(1): 23- 58．

[15]YANDa,WONGRCH,NGW.Efficientmethodsforfindinginfluentiallocationswithadaptivegrids[C]∥Proceedingsofthe20thACMInternationalConferenceonInformationandKnowledgeManagement.NewYork:ACM, 2011: 1475-1484．

[16]CLARKSONKL.Nearestneighborqueriesinmetricspaces[J].DiscreteandComputationalGeometry, 1999, 22 (1): 63-93．

[17]JIChang-qing,LIZhi-yang,QUWen-yu,etal.Scalablenearestneighborqueryprocessingbasedoninvertedgridindex[J].JournalofNetworkandComputerApplications, 2014, 44(1): 172-182．

[18] 张文光,陈俊,姚钰辉,等. 分布式网络环境中基于MapReduce的WordCount实现[J]. 贵州师范大学学报：自然科学版, 2015, 33(1): 93-97．

ZHANGWen-guang,CHENJun,YAOYu-hui,etal.MapReduce-basedWordCountachieveindistributednetworkenvironment[J].JournalofGuizhouNormalUniversity:NaturalSciences, 2015, 33(1): 93-97．

[19]JIChang-qing,QUWen-yu,LIZhi-yang,etal.Scalablemulti-dimensionalRNNqueryprocessing[J].ConcurrencyandComputation:PracticeandExperience, 2015, 27(16): 4156-4171．

[20]JIChang-qing,DONGTing-ting,LIYu,etal.Invertedgrid-basedkNNqueryprocessingwithMapReduce[C]∥ 7thChinaGridAnnualConference(ChinaGrid).Beijing:IEEE, 2012: 25-32.

收稿日期：2012-10-17.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(61370199，61501076)；辽宁省教育科研一般项目(L2014492，L2014283)；国家、辽宁省大学生创新创业训练资助项目(201611258015，201611258040)；辽宁省“十二五”教学改革资助项目(JG14DB037)；大连市科技计划资助项目(20150280)；大连大学博士启动专项基金资助项目(20151QL022)；广东省石化装备故障诊断重点实验室开放基金资助项目(GDUPTKLAB201505)；大连市智慧医疗与健康重点实验室资助项目;中国高等教育学会大学素质教育专题研究课题(CALE201610).

作者简介：季长清(1980-)，男，博士，副教授，从事云计算、大数据、空间数据库、物联网、移动计算等研究.ORCID:0000-0003-3473-2018. E-mail: jcqgood@gmail.com

DOI:10.3785/j.issn.1008-973X.2016.07.015

中图分类号：TP 302

文献标志码：A

文章编号：1008-973X(2016)07-1330-08

Bichromaticreversenearestneighborqueryalgorithminenvironmentofmobilecloudcomputing

JIChang-qing1,2,YUSheng1,WANGBao-feng2,TAOShuai2,WANGZu-min2,WANGRun-fang2

(1.College of Physical Science and Technology, Dalian University, Dalian 116622, China;2.College of Information Technology, Dalian University, Dalian 116622, China)

Abstract:A new and high-efficiency bichromatic reverse nearest neighbor query algorithm-SILM algorithm was designed based on the inverted grid index structure within the MapReduce framework by the study on max bichromatic reverse nearest neighbor query optimization problem in the environment of mobile cloud computing. For the split data area, PCT round algorithm was applied in the Map function and the weight of circular area or grids intersected with the circle was denoted as 1. Then the split data areas were scanned and merged by grid processing algorithms in the Reduce function, and the weights of overlapping grids were accumulated. The grid area with the largest weight of the grid space was outputted. SILM algorithm can not only realize the distributed computation on multiple calculation nodes, but also complete the large-scale parallel query requests in mobile cloud computing environment. The experiment on the high-efficiency of SILM algorithm was conducted. Results show that the efficiency of SILM algorithm is 2 times more than that of the best algorithm on solving the optimal location problem when the number of data points is larger than 2.0×106．

Key words:max bichromatic reverse nearest neighbor; inverted grid index; mobile cloud computing