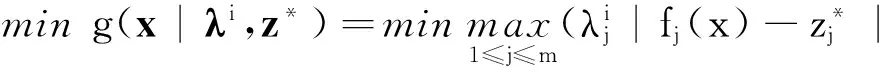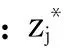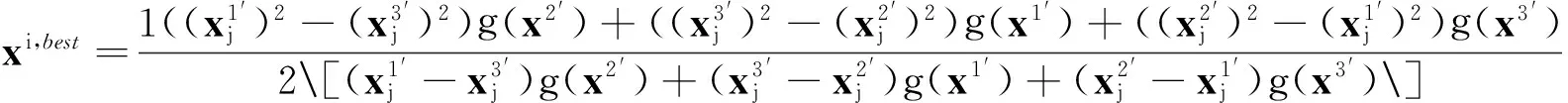新的混合分解高维多目标进化算法

2016-08-04 07:05过晓芳王宇平

浙江大学学报（工学版） 2016年7期

过晓芳,王宇平,代　才

(1. 西安电子科技大学计算机学院,陕西西安 710071；2.西安工业大学理学院,陕西西安 710032)

新的混合分解高维多目标进化算法

过晓芳1,2,王宇平1,代才1

(1. 西安电子科技大学计算机学院,陕西西安 710071；2.西安工业大学理学院,陕西西安 710032)

摘要:在基于分解技术求解高维多目标优化问题的思想启发下,为了提高多目标优化问题非支配解集合的分布性和收敛性,提出新的基于个体支配关系的混合分解高维多目标进化算法.该算法采用分子种群的进化模式,设计新的基于有效阶的个体支配关系用于个体的比较和更新操作,以便在增加个体选择压力的同时提高解集分布的多样性.为了改善该算法的局部搜索性能,将Powell搜索作为局部搜索算子,采用传统优化与进化算法相融合的混合进化策略.为了检验提出算法的性能,将提出算法用于求解5～20个目标的6类标准测试问题,与同类算法相比,该算法在收敛性和分布性方面均具有较大的改进和提高.

关键词：多目标优化问题；进化算法；分子种群；个体支配关系

在科学研究和工程实践领域,越来越多的多目标优化问题涉及到3个或3个以上目标对应的高维多目标优化问题[1](manyobjectiveoptimizationproblems,MAPs),而高维多目标进化算法的研究已经成为进化算法领域的一个研究热点和难点.

随着多目标优化问题的目标个数不断增多,基于Pareto支配的个体排序策略会使种群中的大部分个体具有相同的排序值,此时,进化过程由于缺乏选择压力导致算法的搜索能力急剧下降[2-4].为了增加算法对非支配个体的排序和选择能力,各国学者相继提出两类不同的策略对种群个体进行排序.1)基于松散Pareto支配关系的个体排序策略[5-9]；2)基于评价指标的个体适应度赋值[10-12].这两种方法虽然在一定程度上能够增加个体的选择压力,但是在目标数目较多的问题中有一定的局限性.同时,基于分解技术的多目标进化算法[13](multi-objectiveevolutionaryalgorithmsbasedondecomposition,MOEA/D)的提出为求解高维多目标优化问题提供了一个全新的思路.它将传统的数学规划方法与进化算法相结合,通过聚合函数把一个多目标优化问题分解为若干个单目标优化子问题并行求解.采用该算法有效地求解了具有多个目标的优化问题,得到了越来越多研究者的广泛关注并提出了许多改进方法[14-17].

基于分解的技术在本质上存在一些局限性,在实施子问题解的更新操作中,新产生个体能否被旧个体取代完全取决于其在所属子问题中聚合函数的取值,但未考虑新个体实际所在目标空间的位置,在一定程度上会影响种群的分布性[18-19].Liu等[19]提出新的基于分解思想求解多目标优化问题的算法MOEA/D-M2M,将多目标优化问题分解成相对简单的若干个多目标优化的子问题,然后以并行的方式分别执行进化算法求出每个子问题的非支配解集合,并构成整个的Pareto最优解集合.采用该方法较好地解决了MOEA/D算法中个体更新策略所带来的多样性性能下降的不足,但是在子种群内部所采用的进化策略在某种程度上导致了算法的搜索效率较低.

在基于利用分解的思路求解高维多目标优化问题的思想启发下,为了在改善非支配解集分布性的同时进一步提高算法的收敛性能,本文提出新的基于个体支配关系的混合分解高维多目标进化算法(hybriddecompositionmanyobjectiveevolutionaryalgorithmbasedonnewdominancerelation,HDMOEA-NDR).在HDMOEA-NDR中,首先针对MOEA/D中所采用的权向量设计方法无法任意设置其大小数目的不足,采用均匀设计[19]的方法将目标空间划分成若干个子空间,并利用每个子空间对应的子种群分别实施进化操作,然后挑选出每个子种群的最佳非支配个体作为算法的非支配解集合.在每个子种群中,为了在提高个体选择压力的同时改善种群分布的多样性,设计基于有效阶的个体支配关系用于个体的选择和更新操作.为了提高算法的局部搜索和全局搜索的性能,算法采用传统优化Powell搜索法和进化算法相融合的混合进化策略参与进化操作.

1问题背景

1.1多目标优化问题

定义1多目标优化问题和高维多目标优化问题高维多目标优化问题建立在多目标优化问题的基础上.不失一般性,多目标优化问题(multi-objectiveoptimization,MOP)可以表述为

(1)

定义2Pareto支配对于决策空间中的两个向量xA,xB,xAPareto支配xB(记为xAxB)当且仅当满足

(∀i)(fi(xA)≤fi(xB))∧

(∃j)(fj(xA)

(2)

定义3Pareto最优解或非支配解一个解x*被称为Pareto最优解当且仅当在决策空间中x*不会被其他解x所Pareto支配,其中,表示解个体之间的Pareto支配关系.决策空间中所有的Pareto最优解集合构成了Pareto最优解集(Pareto set, PS),Pareto最优解集中的所有Pareto最优解在目标空间中的像构成了Pareto最优前沿(Pareto front, PF).

(3)

在利用进化算法求解多目标优化问题的过程中,进化算法使用适应度函数引导群体向Pareto最优前沿收敛.在设计算法时需要求出的非支配解集合不断逼近真正的Pareto最优解集,并尽可能均匀且宽广地分布在目标函数空间中.

1.2基于分解的MOEA/D算法的基本思想

MOEA/D是Zhang等[13]提出的一种基于分解思想求解多目标优化问题的算法.它结合传统的数学规划方法与进化算法,将一个多目标优化问题(1)分解为若干个单目标优化子问题,然后用进化算法同时求解这些子问题的最优解作为多目标优化问题的Pareto最优解集合.其中,每一个单目标优化子问题的目标函数对应一个有关特定权向量的聚合函数,MOEA/D利用一组权向量集合来设置不同的搜索方向,不同的权向量将引导算法朝着目标空间的不同区域进行搜索.MOEA/D采用切比雪夫分解方法将多目标优化问题分解成若干个如下式所示的单目标优化的子问题：

(4)

2基于新个体支配关系的混合分解高维多目标进化算法

在基于分解思想求解高维多目标优化问题的思想启发下,为了在进一步提高子问题内部个体向真正Pareto前沿收敛能力的同时改善非支配解集合的分布性,提出新的基于个体支配关系的混合分解高维多目标进化算法(hybrid decomposition many objective evolutionary algorithm based on new dominance relation, HDMOEA-NDR).按照MOEA/D-M2M的进化模式,提出算法首先通过一组均匀分布的方向向量将目标空间划分成若干个子目标空间,与此同时,初始种群被这组方向向量分解成若干个子种群.在每个子种群中,针对高维多目标优化问题中个体之间由于缺乏选择压力而导致收敛性下降的不足,设计新的个体支配关系用来比较非支配个体间的优劣关系,并将该支配关系用于子种群内部个体的选择和更新操作.另外,为了在保证算法全局收敛的同时提高局部搜索性能,提出算法根据进化的前、后阶段自适应地选择不同区域的个体参与新个体的生成,设计一种将传统优化Powell搜索法和进化算法相融合的混合进化策略.

2.1子种群的划分以及个体的更新策略

分子种群的进化策略将高维多目标优化问题划分成若干个子问题同时进化.首先,它利用均匀设计的思想[14]并通过一组均匀分布的方向向量λ1,λ2,…,λN将目标空间划分为若干个子空间,同时,将初始种群POP中的每个个体分配到离其最近的权向量所属的子种群中,从而将初始种群划分为若干个子种群,记为P1,P2,…,PN.子种群的划分规则可以通过下式来实现：

Pi={x|x∈POP,<(F(x)-Z),λi> ≤

<(F(x)-Z),λj>}.

(5)

式中：Z为参考点,Z=[z1,z2,…,zm]T,其中 zi=min{fi(x)|x∈Ω};F(x)-Z为个体x的目标向量与参考点连线的方向向量；<>表示个体的方向向量与权向量的夹角,其取值越小,表示该个体离权向量越靠近.算法1描述了子种群的划分策略.

算法1子种群的分配策略

输入：初始种群POP和方向向量集合λ1,λ2,…,λN.

输出：子种群P1,P2,…PN.

1)按照式(5)将种群中的每个个体并入所对应的子种群P1,P2,…,PN中.

2)对于每个子问题i,执行

IF |Pi|≤K

在种群POP中随机选择(K-|Pi|)个个体放入子种群Pi中；

ELSE

在Pi中随机选出两个个体,根据2.2节提出的有效阶支配关系去掉两者之中的被支配个体,该过程重复(|Pi|-K)次,直到子种群Pi中具有K个个体.

END

2.2基于有效阶的个体支配关系

在高维多目标优化问题中,随着优化目标个数的不断增多,非支配个体在种群中所占的比例迅速上升,甚至种群中的绝大部分个体都变成非支配个体.此时,传统的Pareto支配关系已经无法比较非支配个体间的优劣关系.为了在子种群的进化操作中增加个体间的选择压力并将靠近Pareto前沿的优良个体挑出参与进化操作,设计一种新的基于有效阶的个体支配关系.

定义4基于有效阶的个体支配关系对于定义1给定的多目标优化问题,xA、xB是原始目标集合{f1,f2,…,fm}下基于Pareto支配关系的两个非支配个体,在原始目标集{f1,f2,…,fm}中任取k个目标函数{fi1,fi2,…,fik}(ik∈{1,2,…,m})构成原始目标集的子集(称为目标子集),所有含k个目标函数的目标子集构成的集合记为sk,即sk={P|P⊆{f1,f2,…,fm}∧|P|=k}.下面考虑给定k元目标子集所构成的集合sk中,个体xA与xB的Pareto支配关系.

对于固定的k,nb(xA,xB|k),ne(xA,xB|k)和nw(xA,xB|k)分别表示以sk中元素(fi1,fi2,…,fik)为目标集比较xA、xB支配关系时, 使xAParetoxB、xA和xB具有互不Pareto支配、xBParetoxA关系成立的k元素目标子集的数目,分别记为

nb(xA,xB|k)=|{i|xA{i}xB,∀i∈sk}|,

(6)

ne(xA,xB|k)=|{i|(xA{i}xB)∧

(xB{i}xA),∀i∈sk}|,

(7)

nw(xA,xB|k)=|{i|xB{i}xA,∀i∈sk}|.

(8)

式中：xA{i}xB表示以sk中元素i作为目标集时, 个体xA支配个体xB.

通常,首先取k=m-1,验证两个互不Pareto支配的个体xA、xB在m-1阶的目标子集下是否满足有效阶支配关系.若无法满足其中一个个体能够有效阶支配另一个个体,则考虑它们在m-2阶的目标子集下是否满足有效阶支配关系,依次类推.

依次分析在Pareto支配关系和有效阶支配关系下比较两个个体优劣的时间复杂度,分别为O(mN2)和O(2mmN2),其中,m为目标数,N为进化种群规模.尽管后者的时间复杂度高于前者,但是基于有效阶的个体支配关系能够有效地区分出两个个体的优劣关系.在一般情况下,只需考察个体在k=m-1阶目标子集下的有效阶支配关系便可以区分两两非支配个体间的优劣,因此时间复杂度远远达不到O(2mmN2).另外,与传统的基于Pareto的个体支配关系相比,在每个子种群中采用基于有效阶的个体支配关系的优越性如下.1)改善了高维多目标优化问题中个体之间由于缺乏选择压力而导致收敛性下降的不足；2)弥补了仅用聚合函数评估个体优劣导致种群多样性下降的缺陷.

2.3混合进化策略

在每个子种群的进化操作中,为了提高算法的局部搜索和全局搜索的性能,融合进化算法和传统优化算法,在进化的不同阶段自适应地选择不同区域的个体参与新个体的生成.在进化过程的前期,为了增强算法的全局搜索能力,以较大的概率选择其他子种群的个体进行交叉操作；在进化过程的后期,将传统优化的Powell搜索法作为局部搜索算子来产生新的个体,以此来提高算法的收敛速度.

Powell法是一类经典、简单有效的直接搜索方法,它在函数寻优的过程中仅仅借助函数值本身的信息,在优化问题中很方便使用.Powell法反复利用3个点的切比雪夫目标函数信息进行二次插值来逼近函数真正的极小值点,计算量相对较小.Powell法非常适合作为一种启发式局部搜索算子融入到MOEA/D的进化操作中,以提高解的精度.

在每个子种群内部,Powell局部搜索算子随机选出其中的任意两个个体和与该子种群内的当前最好个体构成3个初始点,分别记为x1、x2和xi,best,利用式(4)计算当前3个个体对应在所在子空间i中的切比雪夫函数值,并按照函数值的大小关系对三个个体予以重新排序x1′、x2′、x3′,其中g(x1′)

(9)

式中：过三点(x1′,g(x1′))、(x2′,g(x2′))和(x3′,g(x3′))作一个二次多项式,并用该二次多项式的极小值点作为原函数极小值点的近似.此时,根据多元函数极值点存在的必要条件,利用二次函数的导数为0作为原函数极小值点的近似,即为xi,best.将新产生的最优点xi,best和原先3个个体x1′、x2′、x3′的切比雪夫函数值进行比较,并去掉最差的一个点,利用余下的3个点继续作二次插值,重新得到新的最小值点yi,best.如此继续作二次插值,直到满足一定的精度后停止.

2.4基于新的个体支配关系的分解高维多目标进化算法

在执行过程中,设置的参数有：子问题(权重向量)的个数N,每个子问题对应的子种群的规模K,每个权重向量的邻居权向量的个数T,执行选择操作时用到的参数J,函数总共的评估次数Ev.算法的具体描述如下.

算法2HDMOEA-NRS主流程

1)初始化.

a)采用均匀设计[11]的方式产生N个权重向量λ1,λ2,…,λN.

b)随机产生一个规模为N×K的初始化种群,x1,x2,…,xN×K,并计算初始种群的参考点Z=[z1,…,zm]T.

c)利用算法1将初始种群划分为N个子种群,并且每个子种群中包含K个解,例如第i个子种群的个体记为{xi(K-1)+1,xi(K-1)+2,…,xiK},计算每个子种群的最好个体并将其记录在xNK上.

d)计算两两权向量间的欧氏距离,对于每个子问题i,将邻居向量设置为B(i)=[i1,…,iT].

2)更新操作.对于每个子问题i对应的子种群,随机产生一个随机数r.根据随机数与选择操作参数J的大小关系,选择位于不同区域的个体参与不同的交叉操作,以便增加算法的局部搜索和全局搜索能力.

3)选择和交叉操作.若随机数r

4)变异操作.对交叉操作后生成的新个体y执行变异操作,生成新个体y′.

5)更新操作.用新个体y′更新参考点Z,并根据式(5)判断新个体y′找到所属的子种群Pl.比较y′与子种群Pl的最好个体xlK的有效阶支配关系：当y′kxlK时,将新个体y′保留在子种群Pl中,并在子种群Pl中的其余K-1个个体中随机删除一个；当xlKky′时,将新个体y′舍弃.

3)判断终止准则.

若终止条件满足,则将每个子种群的最好个体作为最终种群输出；否则,转步骤2).

3实验结果与分析

3.1实验设计和参数设置

为了检测HDMOEA-NRS算法的性能,将该算法用于求解5类目标数可扩展的测试问题,分别包括具有多个局部Pareto Front的测试问题DTLZ1、DTLZ2和DTLZ3[20]以及具有复杂Pareto Set的测试问题F1和F2[21].每个测试问题所求解的目标数分别为5、10、15和20,并将数值试验的测试结果与三类的高维多目标进化算法,分别是采用分子种群的多目标进化算法MOEA/D-M2M[19]、均匀权向量设计的分解多目标进化算法UMOEA/D[14]和基于收缩和扩展支配域的多目标进化算法NSGAII-CE[22]所得到的实验结果进行比较.

针对数值实验中的每一个测试问题,4种算法(HDMOEA-NRS, MOEA/D-M2M,UMOEA/D和NSGAII-CE)采用相同的进化算子,个体均采用实数编码,具体参数设置如下.1) 种群规模：HDMOEA-NRS、MOEA/D-M2M、UMOEA/D和NSGAII-CE的种群规模设置为N=200, HDMOEA-NRS采用Beume等[11]提出的均匀设计的方式产生权向量集合,邻居向量|B(i)|=20,每个子种群中包含的个体数K=5.2)进化操作采用差分进化和多项式变异：在差分进化操作中,交叉概率为0.5,比例因子为0.5；在多项式变异操作中,分布指数为20,变异概率为0.1.3)4个算法对于每个测试问题的最大函数评估次数为400 000.4)选择操作参数J为

式中：maxEv为函数的最大评估次数.

在该数值实验中,采用IGD[23](inverted generational distance)指标来度量算法的性能.IGD指标可以同时度量算法所获得非支配解集合的收敛性和分布性,其取值越小,算法的性能越好.每种算法对每个测试问题独立运行20次,分别记录IGD指标在20次运行后计算出的均值和方差.

为了验证在基于子种群的分解多目标进化算法中引入个体新支配关系和局部搜索策略对于算法收敛性的影响,将提出算法HDMOEA-NRS和MOEA/D-M2M针对5、10、15、20目标的测试问题DTLZ2分别独立运行20次,分别记录GD (generational distance)指标在20次运行后计算出的均值和方差.其中,GD[23]指标是用来度量算法所获得非支配解集合的收敛性能,取值越小,算法的收敛性越好.

3.2对比实验结果

表1给出3种算法独立运行20次计算出非支配解集合IGD指标的均值mean和方差std结果,对比同一测试问题在3种不同算法下的IGD指标均值,最优结果在表1中用黑体加粗显示.为了验证提出算法HDMOEA-NRS的性能与同类高维多目标进化算法相比的稳定性,依次对每种算法独立运行20次后得到的IGD指标样本数据进行显著性水平为0.05的t检验,检验结果如表1所示.在每一行所对应的测试问题中,“+”,“-”,“=”分别表示提出算法HDMOEA-NRS的性能优于、劣于或者等于所比较算法.

表1　3种算法在不同测试函数时分别运行10次得到的IGD统计结果

图1　2种算法针对5、10、15、20目标的测试问题DTLZ2的GD指标统计盒图Fig.1　Statistical box diagram of two algorithms in DTLZ2 with 5,10,15,20 objectives

从表1可以看出,前两种算法HDMOEA-NRS和MOEA/D-M2M的IGD指标均值远远优于UMOEA/D和NSGAII-CE,说明通过采用分子种群分解技术的高维多目标进化算法HDMOEA-NRS和MOEA/D-M2M获取的非支配解集合的收敛性和多样性明显优于采用均匀权向量的分解多目标进化算法UMOEA/D,也优于仅仅通过增加个体选择压力的方式来增加收敛性的算法NSGAII-CE.另一方面,对比HDMOEA-NRS和MOEA/D-M2M,提出算法HDMOEA-NRS的IGD均值在大多数测试问题中优于MOEA/D-M2M,表明算法提出的基于子种群内部的个体排序策略和Powell搜索在提高算法的收敛性能方面的有效性和合理性.

图1 给出提出算法HDMOEA-NRS和MOEA/D-M2M针对5、10、15、20目标的测试问题DTLZ2分别独立运行20次计算的GD指标的统计盒图,它能够完整地反映数据的离散分布的统计特性.图中,盒子的上、下两条边界线分别表示样本数据的上、下四分位数,盒子中间的水平线表示样本的中位数.从图1可以看出,当目标数为5时,2种算法的GD指标均值相差不大；但是当目标数较多时,算法HDMOEA-NRS的收敛性明显优于MOEA/D-M2M.

3.3个体新支配关系和局部搜索策略对于算法性能的影响分析

为了验证提出的基于有效阶的个体支配关系对算法收敛性和分布性的影响,对提出算法HDMOEA-NRS进行调整,将基于Pareto支配关系用于子种群内部个体间优劣关系的比较和个体更新操作,而其他进化算子和参数设置保持不变.针对5、10、15、20个目标的测试问题DTLZ1,将HDMOEA-NRS与调整后的采用Pareto排序的算法分别独立运行20次,将计算出的IGD指标均值进行比较,结果如图2所示.可以看出,提出算法将基于有效阶的个体支配关系用于子种群内部个体间优劣关系的比较和个体更新操作,获得的Pareto非支配解集合的收敛性和分布性具有更强的优势.

为了验证采用的Powell局部搜索策略对于算法收敛性和分布性的影响,对提出算法HDMOEA-NRS进行调整,在子种群的进化操作中取消了Powell局部搜索,而其他进化算子和参数设置保持不变.针对5、10、15、20个目标的测试问题DTLZ1,将HDMOEA-NRS与调整后算法分别独立运行20次,将计算出的IGD指标均值进行比较,结果如图3所示.可以看出,当目标数为5时,是否采用局部搜素算子对算法性能的影响不大,但是当目标数较多时,采用局部搜索算子能够较好地提高算法的收敛性能.

图2　2种排序策略对于算法性能的影响Fig.2　Influence of performance with two ranking strategy

图3　局部搜素算子的运用对于算法性能的影响Fig.3　Influence of performance with use of local search operator

3.4参数敏感性分析

为了测试不同的实验参数设置对于算法性能的影响,针对测试问题DTLZ1(5),分别检验权向量的邻居个数T和子种群的规模K对IGD性能指标的影响.首先,在保持其他参数不变的情况下,测试当T的取值分别为5、8、12、15、20、25、30时,分别独立运行HDMOEA-NRS算法20次计算出IGD指标的均值结果进行比较,结果如表2所示.表2的数据表明,T的设置对IGD指标的扰动仅为4%,说明T对算法的性能影响不大.在算法的执行过程中,T的取值越大,表明算法的全局搜索能力越强,本文取T=20.

为了验证不同的子种群规模K对算法性能的影响,在保持其他参数不变的情况下,测试当K的取值分别为5、7、9、11、13、15时,分别独立运行HDMOEA-NRS算法20次计算出IGD指标的均值结果进行比较,结果如表3所示.表3的数据表明, K的设置对IGD指标的扰动仅为3.7%,说明K对算法的性能影响不大.子种群的规模越大,计算过程中函数的评估次数越多,从而增大了算法的计算量.取最小值K=5.

表2　不同的邻域规模T的设置对IGD的影响

表3　不同的子种群规模K的设置对IGD的影响

4结语

为了进一步改善高维多目标优化算法中非支配解集合的分布性和收敛性,在基于分解技术的思想启发下,提出基于新个体支配关系的混合分解高维多目标进化算法.本文的主要贡献在于设计新的基于有效阶的个体支配关系用于子种群内部个体间优劣关系的比较和子种群的更新操作,在增加个体的选择压力的同时提高解集分布的多样性；提出将Powell搜索作为局部搜索算子与进化算法相融合的混合进化策略,以提高基于分解算法的求解精度.实验结果表明,HDMOEA-NRS算法在提高算法的收敛性和改善非支配解集分布的多样性上是有效的.

参考文献 (References):

[1]CHRISTIANVL.Asurveyonmulti-objectiveevolutionaryalgorithmsformany-objectiveproblems[J].ComputationalOptimizationandApplications, 2014, 58(3):707-756．

[2] 公茂果,焦李成,杨咚咚,等. 进化多目标优化算法研究[J]. 软件学报,2009, 2(20): 271-289．

GONGMao-guo,JIAOLi-cheng,YANGDong-dong,etal.Researchonevolutionarymulti-objectiveoptimizationalgorithms[J].JournalofSoftware, 2009, 2(20): 271-289．

[3] 孔维健. 高维多目标进化算法研究综述[J]. 控制与决策, 2010,25(3)：321-326．

KONGWei-jian.Surveyonlarge-dimensionalmulti-objectiveevolutionaryalgorithms[J].ControlandDecision, 2010, 25(3): 321-326．

[4] 巩敦卫. 基于集合的高维多目标优化问题的进化算法[J]. 电子学报, 2014, 42(1): 77-83．

GONGDun-wei.Solvingmany-objectiveoptimizationproblemsusingset-basedevolutionaryalgorithms[J].ActaElectronicaSinica, 2014, 42(1): 77-83．

[5]PIERRODF,KHUST,SAVICDA.Aninvestigationonpreferenceorderrankingschemeformulti-objectiveevolutionaryoptimization[J].IEEETransactionsonEvolutionaryComputation, 2007, 11(1): 17-45．

[6]ZOUXiu-fen,CHENYu,LIUMin-zhong.Anewevolutionaryalgorithmforsolvingmany-objectiveoptimizationproblems[J].IEEETransactionsonSystems,Man,andCybernetics,partB-Cybernetics, 2008, 38(5): 1402-1412．

[7]MOLINAJ,SANTANAL,HERNANDEZ-DIAZA,etal.G-dominance:referencepointbaseddominanceformultiobjectivemetaheuristics[J].EuropeanJournalofOperationalResearch, 2009, 197(2): 685-692．

[8]DEBK,JAINH.Anevolutionarymany-objectiveoptimizationalgorithmusingreference-point-basednondominatedsortingapproach,parti:solvingproblemswithboxconstraints[J].IEEETransactionsonEvolutionaryComputation, 2014, 18(4): 577-601.

[9]YUANYuan,HUAXu,WANGBo.Anewdominancerelationbasedevolutionaryalgorithmformany-objectiveoptimization[J].IEEETransactionsonEvolutionaryComputation, 2016,20(1): 16-37．

[10]ZITZLERE,SIMONK.Indicator-basedselectioninmulti-objectivesearch[C]∥ConferenceonParallelProblemSolvingfromNature(PPSNVIII).UK:Springer, 2004: 832-842．

[11]BEUMEN,NAUJOKSB,EMMERICHM.SMS-EMOA:multiobjectiveselectionbasedondominatedhypervolume[J].EuropeanJournalofOperationalResearch, 2007, 181(3): 1653-1669．

[12]WHILEL,BRADSTREETL,BARONEL.Afastwayofcalculatingexacthypervolumes[J].IEEETransactionsonEvolutionaryComputation, 2012, 16(1): 86-95．

[13]ZHANGQ,LIH.MOEA/D:amultiobjectiveevolutionaryalgorithmbasedondecomposition[J].IEEETransactionsonEvolutionaryComputation, 2007, 11(6): 712-731．

[14]TANYan-yan,JIAOYong-chang,LIHong.MOEA/D+uniformdesign:anewversionofMOEA/Dforoptimizationproblemswithmanyobjectives[J].ComputersandOperationsResearch, 2013, 40(6): 1648-1660．

[15]JIANGS,CAIZ,ZHANGJ,etal.MultiobjectiveoptimizationbydecompositionwithPareto-adaptiveweightvectors[C]∥Proceedingof7thInternationalConferenceonNaturalComputation.Shanghai:IEEE, 2011: 1260-1264．

[16]LIH,ZHANGQ.MultiobjectiveoptimizationproblemswithcomplicatedParetosets,MOEA/DandNSGA-II[J].IEEETransactionsonEvolutionaryComputation, 2009, 13(2): 284-302．

[17]ZHOUA,ZHANGQ,ZHANGG.Amultiobjectiveevolutionaryalgorithmbasedondecompositionandprobabilitymodel[C]∥IEEECongressonEvolutionaryComputation. [S.l.]:IEEE, 2012: 1-8.

[18]QIY.MOEA/Dwithadaptiveweightadjustment[J].EvolutionaryComputation, 2014, 22(2): 231-264．

[19]LIUHai-lin,GUFang-qing,ZHANGQing-fu.Decompositionofamulti-objectiveoptimizationproblemsintoanumberofsimplemulti-objectivesub-problems[J].IEEETransactionsonEvolutionaryComputation, 2014, 18(3): 450-455．

[20]DebK,THIELEL,LAUMANNSM,etal.Scalablemultiobjectiveoptimizationtestproblems[C]∥IEEECongressonEvolutionaryComputation(CEC’02). [S.l.]:IEEE, 2002: 825-830．

[21]ZHANGQ,ZHOUA,ZHAOS,etal.Multi-objectiveoptimizationtestinstancesfortheCEC2009specialsessionandcompetition[R].Clemson:UniversityofEssex, 2008．

[22] 代才. 基于分解的多目标进化算法研究[D]. 西安：西安电子科技大学,2014: 50-70．

DAICai.Researchonevolutionaryalgorithmsbasedondecompositionformany-objectiveoptimizationproblems[D].Xi’an:XidianUniversity, 2014: 50-70.

[23]ZITZLERE,LAUMANNSM,THIELEL.Performanceassessmentofmulti-objectiveoptimizers:analysisandreview[J].IEEETransactionsonEvolutionaryComputation, 2003, 7(2): 117-133.

收稿日期：2015-04-24.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(61472297，61272119，61402350，61502290);陕西省教育厅专项科研资助项目(16JK1381).

作者简介：过晓芳(1981-)，女，博士，讲师，从事多目标进化算法的研究. ORCID: 0000-0002-8944-3400. E-mail: gxfang1981@126.com

DOI:10.3785/j.issn.1008-973X.2016.07.013

中图分类号：TP 301

文献标志码：A

文章编号：1008-973X(2016)07-1313-09

Newhybriddecompositionmany-objectiveevolutionaryalgorithm

GUOXiao-fang1,2,WANGYu-ping1,DAICai1

(1. School of Computer, Xidian University, Xi’an 710071, China;2. School of Science, Xi’an Technological University, Xi’an 710032, China)

Abstract:A hybrid decomposition many-objective evolutionary algorithm based on a new dominance relation was proposed inspired by many-objective evolutionary algorithms based on decomposition in order to improve the diversity and convergence of the non-dominated solution set in many-objective optimization problems. The sub-population evolutionary pattern was adopted, and a new efficiency order based dominance relation was designed to compare and update individuals inside each subpopulation, which helps to increase selective pressure and improve diversity. Powell search was used as the local search operator in order to improve the performance of local search. A hybrid evolution strategy combining traditional optimization method with evolutionary algorithm was adopted. Six standard benchmark problems with 5 to 20 objectives were tested to demonstrate the effectiveness of the algorithm. Experimental results showed that the algorithm performed better than other available algorithms in convergence and diversity．

Key words:many-objective optimization problem; evolutionary algorithm; subpopulation; dominance relation

浙江大学学报（工学版）2016年7期

浙江大学学报（工学版）的其它文章: 竖向荷载对黏土地基中单桩水平受荷性能的影响; 超高层建筑横风向风振局部气动外形优化; 动车组过隧道时设备舱气动效应动模型试验; 转向系统传递函数的研究及理想传动比获取; 基于两级过滤的时间序列近似查询; 基于混合势场的移动机器人视觉轨迹规划