基于多传感器信息融合的涡街信号处理方法

宋开臣,曾　瑶,叶凌云

(浙江大学 生物医学工程与仪器科学学院,浙江 杭州 310027)



基于多传感器信息融合的涡街信号处理方法

宋开臣,曾瑶,叶凌云

(浙江大学 生物医学工程与仪器科学学院,浙江 杭州 310027)

摘要:针对压电式涡街流量计抗干扰性能差的缺点,提出基于多传感器信息融合的涡街信号检测方法.在该测量系统中,差压传感器测得钝体前、后的平均差压,压电传感器检测钝体下游涡街信号的频率,通过无迹卡尔曼滤波(UKF)算法将以上两种信息进行数据融合,有效提高了数字带通滤波器的锁定精度.在搭建的振动实验平台上验证了该方法的可行性,对比分析了本文方法和传统方法的测量结果.实验表明：采用该处理方法能够有效抑制外界的强振动噪声干扰对流速测量的影响,当最大振动噪声干扰的强度为涡街信号的4倍时,测量精度可以达到1%,增强了压电式涡街流量计的抗振能力,提高了流量测量精度.

关键词：压电式涡街流量计；多传感器信息融合；无迹卡尔曼滤波；抗振能力

涡街流量计是根据著名的“卡曼涡街”[1-4]原理实现流量测量的流量计,具有无机械可动部件、安装方便、量程比较宽等优点,被广泛应用于石油化工领域.压电式涡街流量计是在工业现场普遍使用的涡街流量计,主要测量部件为压电传感器,因为压电式涡街流量计容易受到管道振动干扰.特别是当振动信号的能量与涡街信号的能量相近,甚至是强于后者时,在时域中,振动信号与涡街信号叠加无法分辨；在频域中,两者幅值接近,频谱分析等现有的数字信号处理方法将失效.徐科军等[5-6]对涡街信号及振动信号模型进行分析,采用数字滤波和自相关相结合的算法消除强噪声干扰,在一定程度上消除了强振动干扰对流量测量的影响.针对双涡街传感器的流量计,徐科军等[7]提出采用频域相减与频率方差计算相结合的方法来处理涡街流量传感器输出信号,取得了很好的实验效果.

1基于多传感器信息融合的流量测量系统

提出的多传感器流量测量系统由压电传感器和差压传感器共同组成,如图1所示.

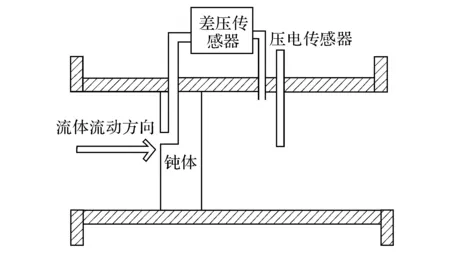
图1　多传感器涡街流量计测量系统示意图Fig.1　Map of multi-sensor vortex flowmeter’s measurement system

图2　三棱柱钝体截面图Fig.2　Sectional drawing of triangular prism bluff body

图1中的钝体为坡度较小、顶角朝后的三棱柱钝体(见图2)；与普通压电式涡街流量计一样,压电传感器安装在钝体下游,检测旋涡分离产生的涡街信号.在一定的雷诺数范围内,旋涡分离的频率f与管道内流体的平均流速U和发生体的特征长度d之间的关系可以表示为

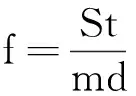
(1)

式中：St为斯特劳哈尔数(无量纲),对于一定形状的旋涡发生体,在一定的雷诺数范围内,St是一个常数；m为发生体两侧弓形流通面积与测量管道横截面面积之比,m与d和测量管道内径D之间的关系可以表示为

(2)

从式(1)、(2)可以看出,对于确定的D和d,涡街信号频率仅与流体的流速成正比,与被测流体的压力、温度、黏度和组成变化无关,因此通过涡街信号测得流速的精度较高.由于压电传感器对管道振动很敏感,振动噪声干扰对涡街信号测量的影响很大.

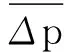
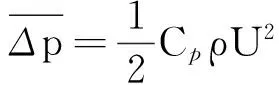
(3)

式中：Cp为阻力系数,正常测量时Cp为常数；ρ为流体密度；U为流体流速.

在该测量系统中,差压传感器的正取压口位于钝体内部的迎流面,负取压口位于钝体的下游1.5D处.差压传感器两端测得的是钝体迎流面上的全压力和钝体下游的静压力之差[1].

管道振动对差压传感器测量的影响很小,差压传感器的抗振性能很强,但是受差压传感器测量精度和流体密度计算精度的影响,直接通过差压传感器测得的流速精度较低.

综合利用涡街信号测量精度高和钝体前、后的差压信号抗振性能强的优点,采用基于UKF算法的多信息融合算法,利用差压传感器测得钝体前、后的平均差压作为辅助信号来提高压电传感器检测涡街信号频率的精度,增强压电式涡街流量计的抗振性能.

2基于UKF算法的多信息融合处理

2.1UKF算法在涡街信号处理中的应用

卡尔曼滤波被称为最优化自回归数据处理算法,国内外学者对于卡尔曼滤波算法的研究已有五十几年的历史,卡尔曼滤波器是在时域内设计,且适用于多维情况,具有很好的鲁棒性和实时性,广泛应用于重要的国防工业领域[12].卡尔曼滤波使用状态更新和测量值反馈的方法来估计状态：更新某一时刻的状态预测值,然后以含有噪声的观测变量获得反馈,计算得到卡尔曼滤波增益,得到这一时刻的状态估计值[13-15].卡尔曼滤波可以分为时间更新和测量更新两个过程.时间更新过程计算当前时刻的状态变量和协方差的预测值,测量更新程则进行测量的反馈.卡尔曼滤波算法的循环跟新过程如图3所示.

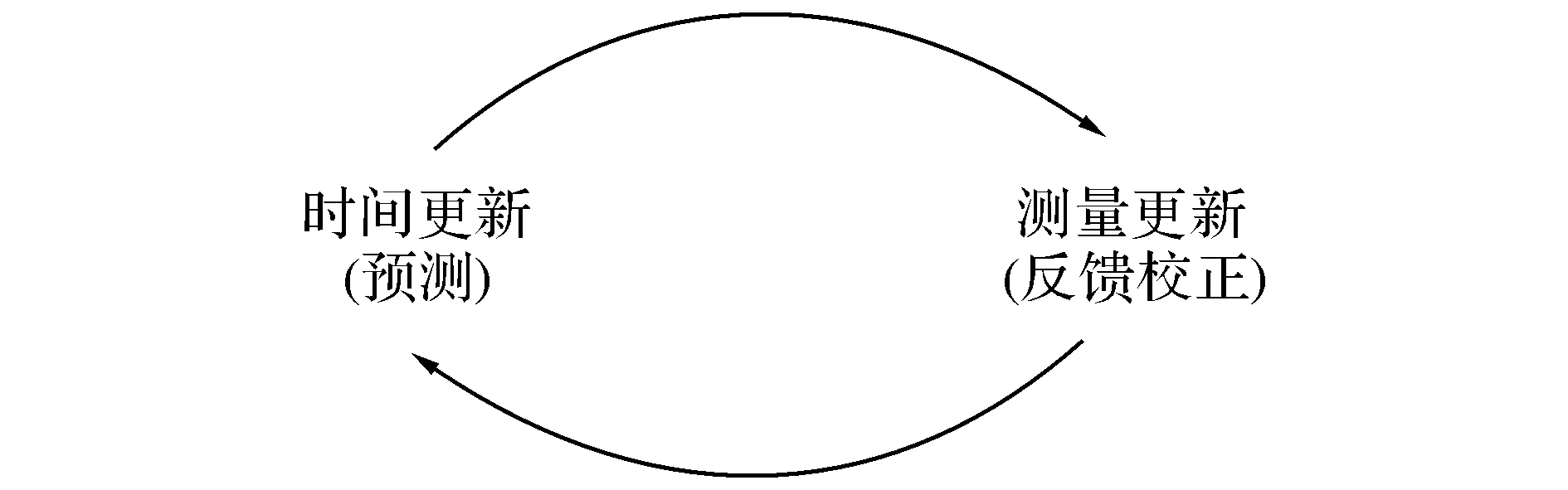
图3　卡尔曼滤波循环更新过程Fig.3　Cycle renewal process of Kalman filter

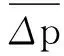
(4)

式中：k1、k2均为常数,

k1=Cρ/2,k2=St/(md).

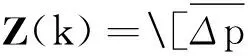
由式(4)可知,状态向量处于非线性状态,须采用非线性卡尔曼滤波算法对状态向量进行求解.UKF算法是比较常用的非线性卡尔曼滤波算法.滤波以无偏变换[16-17]为基础,采用确定性采样策略近似非线性分布,选取有限个Sigma采样点来近似系统状态的先验统计特性,再直接通过非线性方程演化系统状态的后验分布特性.

UKF的状态方程和测量方程如下：

(5)

由式(4)可知,在研究的系统中,状态方程中的F(Xk-1)可以表示为

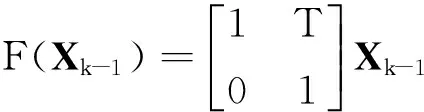
(6)

式中：T为测量更新的时间.

测量方程H(Xk)可由下列2个矩阵方程表示：

(7)

2.2多传感器信息融合算法的实现

基于多传感器信息融合算法的涡街信号处理方法的原理框图如图4所示.

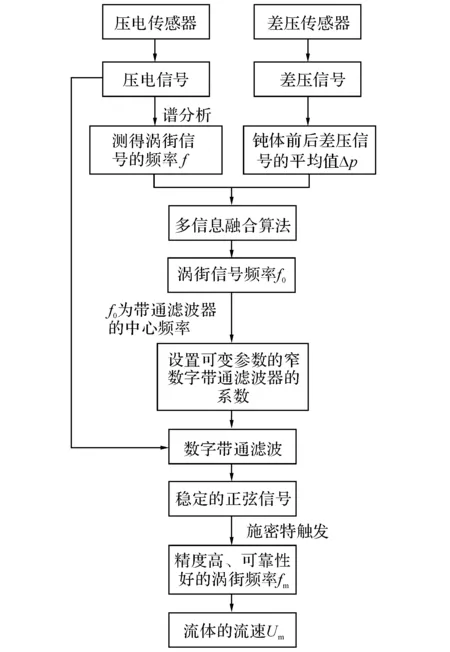
图4　涡街信号处理方法的原理框图Fig.4　Principle block diagram of vortex signal processing method

上述原理框图中的多信息融合算法分为以下4个步骤实现.

2)对经过信号调理电路之后的压电信号进行谱分析,记录频谱图中的最高峰值、次高峰值、第三和第四高峰值对应的频率fn(n=1,2,3,4).

3)若fn中存在与fp相差不大的频率,即存在fn(n=1,2,3,4)使|fn-fp|<Δf时,在fn中找出与fp最接近的一个值作为压电信号谱分析的最终结果f,即在fn(n=1,2,3,4)中找出使|fn-fp|最小的值,然后执行步骤4)；若fn中的所有值都与fp相差较大,即当|fn-fp|≥Δf(n=1,2,3,4)时,不执行步骤4),直接将fp作为带通滤波器的中心频率f0.

通过现场标定获得不同流量点下的Δf,在标定过程中,通过管道上的标称流量计得到有用涡街信号的频率fs,通过步骤1)的方法得到频率fp,则Δf=|fs-fp|.保持管道内流体流量恒定,测量多组Δf的值,取Δf的平均值作为该流量下Δf的最终值.改变管道内流体的流量,选取若干个不同的流量,采用上述方法测得不同流量下的Δf.通过曲线拟合的方式,得到涡街流量计在流量测量范围之内的所有流量点下的Δf.

优于传统压电式涡街流量计的信号处理方法,在步骤3)中,没有将频谱图中最高峰值对应的频率作为压电信号的频率,而是将最接近fp的频率作为谱分析的结果,提高了整个测量系统对有用涡街信号的跟踪性能.步骤3)是整个信息融合算法中的重要一步.

3实验验证

为了验证提出的多传感器信息融合测量方法的可行性,以DN50口径的压电式涡街流量计为例,在测量管道受到强振动的情况下,分别采用传统测量方法[18-19]和提出的方法对流速进行测量,用图形显示2种方法的测量结果,并对2种测量方法的测量误差进行比较和分析.

在实验过程中,通过实验装置上的标称流量计获得管道内流体的流速及涡街信号频率.用鼓风机模拟气体流量,并将调速电机安装在管道上(见图5),电机的振动带动管道的振动,通过调节电机的转速可以调节电机振动的频率.在电机的转轴上安装一个偏心轮,用来增强管道振动的强度,使管道振动作用在压电传感器上的噪声信号强度大于涡街信号的强度.

图5　振动实验装置Fig.5　Vibration experiment equipment

选取3个不同的流量点进行实验,分别为81.15Hz(4.28m/s)、180.98Hz(8.99m/s)和296.66Hz(14.57m/s),括号内的值表示该涡街信号频率对应的气体流速.以振动信号频率为89.58和141.70Hz、涡街信号为177.10Hz的流量点为例,如图6(a)、(b)所示分别为差压传感器和压电传感器输出信号经过信号调理电路之后的波形图,信号的采样率为32kHz.图中，UV为电压.如图6(c)所示为压电传感器输出信号的功率谱.从图6(c)可以看出,管道振动信号的能量大于涡街信号的能量.

如图6(d)所示为传统方法的测量结果,传统的测量方法是直接将频谱图中的最高峰值对应的频率作为数字带通滤波器的中心频率,在15～45单位时间段内,当管道振动频率与涡街信号的频率相差很大时,传统测量方法的测量值与真实值偏差很大,不能实现流量的正常测量.如图6(e)所示为本文方法的测量结果,采用提出的基于多信息融合算法的涡街信号处理方法能够削弱甚至是消除管道振动噪声的干扰,在第2个单位时间处,数字带通滤波器的中心频率已经接近涡街信号的真实频率,并逐步向真实频率进行收敛,最终的测量结果明显优于传统方法.

如表1所示为当气体流量频率分别为81.15、180.98和296.66Hz时,本文方法和传统方法的最终测量结果.表中，fV为振动频率，fu为涡街信号频率，fm为本文测得的频率，Et为传统方法的测量误差，Ek为本文方法的测量误差.可以看出,在测量管道受到周期性强振动的情况下,传统测量方法的测量误差超过20%；当涡街信号频率较低时,测量误差超过30%.本文提出的测量方法的平均相对误差远小于传统方法,测量精度更高.

表1本文方法与传统方法的平均相对误差比较

Tab.1Averagerelativeerrorinthispapervstraditionalmethod

fV/Hzfu/Hzfm/HzEt/%Ek/%68.75、118.80、137.5081.1579.9833.251.4789.58、141.70180.98182.7322.430.97150.22296.66299.4820.870.95

4结语

本文提出多传感器检测方法的流量测量方案,采用基于UKF算法的多传感器涡街信号处理方法,解决了压电式涡街流量计抗强振动干扰性能差的缺点.实验表明,当噪声振动干扰的能量高于涡街信号的能量时,采用多传感器涡街信号处理方法,有效抑制了强振动噪声对流量测量的影响,测量结果明显优于传统的测量方法.当气体流速为8.99和14.57m/s时,测量精度可以达到1%；当气体流速较小时,测量精度可以达到1.5%,达到预期要求.

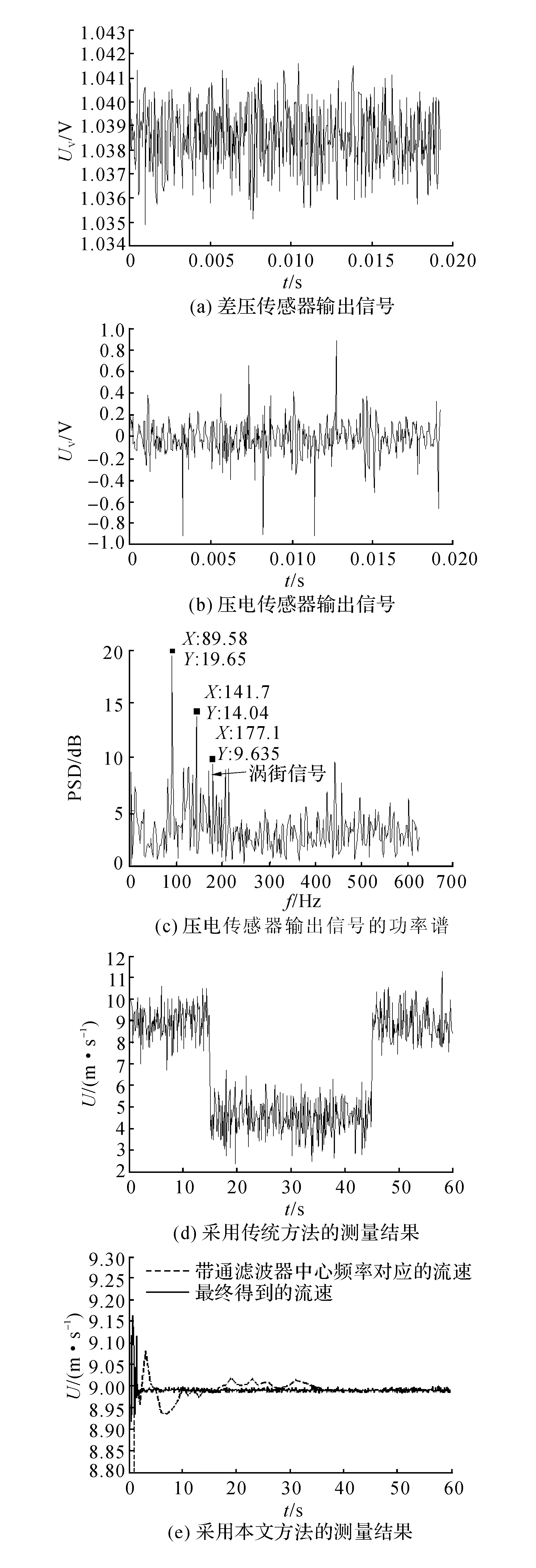
图6　本文振动实验的测量结果Fig.6　Measurement result of experiment in this paper

参考文献(References):

[1]黄咏梅. 基于差压原理的涡街质量流量测量方法研究[D]. 杭州：浙江大学, 2005．

HUANGYong-mei.Researchonmassflowratemeasurementusingvortexflowmeterbasedondifferentialpressureprinciple[D].Hangzhou:ZhejiangUniversity, 2005．

[2]潘岚, 宋开臣, 徐国梁. 高抗干扰性能涡街流量计传感器的研究[J]. 中国计量学院学报, 2005,16(4): 268-270．

PANLan,SONGKai-chen,XUGuo-liang.Researchonthesensorofvortexflowmeterwithinterferenceresistant[J].JournalofChinaJiliangUniversity, 2005, 16(4): 268-270．

[3]VENUGOPALA,AGRAWALA,PRABHUSV.FrequencydetectioninvortexflowmeterforlowReynoldsnumberusingpiezoelectricsensorandinstallationeffects[J].SensorsandActuatorsA:Physical, 2012, 184: 78-85.

[4]VENUGOPALA,AGRAWALA,PRABHUSV.Influenceofblockageandupstreamdisturbancesontheperformanceofavortexflowmeterwithatrapezoidalbluffbody[J].Measurement, 2010, 43(4): 603-616．

[5]徐科军, 王沁, 方敏, 等. 基于数字滤波与自相关的涡街流量计抗强振动方法改进[J]. 计量学报, 2014, 35(5): 449-454．

XUKe-jun,WANGQin,FANGMin,etal.Improvementofanti-strong-vibrationmethodcombingdigtalfilterwithauto-correlationforvortexflowmeter[J].ActaMetrologicaSinica, 2014, 35(5): 449-454．

[6]王沁. 抗强振型涡街流量计和快速响应型压电式阀门定位器软件研制[D]. 合肥：合肥工业大学, 2012．

WANGQin.Softwaredevelopmentforthevortexflowmeterofanti-strongvibrationandpiezoelectricvalvepositionerofquickresponse[D].Hefei:HefeiUniversityofTechnology, 2012．

[7]徐科军, 方敏, 罗清林, 等. 抗振型低功耗数字涡街流量计研制[J]. 计量学报, 2013, 34(5): 435-440．

XUKe-jun,FANGMin,LUOQing-lin,etal.Developmentofanti-vibration-typevortexflowmeterwithlowpoweranddigitalprocessing[J].ActaMetrologicaSinica, 2013, 34(5): 435-440．

[8]孙志强, 张宏建, 黄咏梅, 等. 管壁差压式涡街流量计测量影响因素分析[J]. 浙江大学学报：工学版, 2006, 40(12): 2103-2106．

SUNZhi-qiang,ZHANGHong-jian,HUANGYong-mei,etal.Impactanalysisofvortexflowmetermeasuredwithduct-walldifferentialpressuremethod[J].JournalofZhejiangUniversity:EngineeringScience, 2006, 40(12): 2103-2106．

[9]MINUJJ,YEHCF,HUCC,etal.Onmeasurementuncertaintyofavortexflowmeter[J].FlowMeasurementandInstrumentation, 2005, 16(6): 397-404．

[10]王子麒. 差压式涡街流量计仪表优化设计与涡街信号处理的研究[D]. 杭州：浙江大学, 2008．

WANGZi-qi.Optimizationofthedifferentialpressurebasedvortexflowmeterandresearchofvortexsignalprocess[D].Hangzhou:ZhejiangUniversity, 2008．

[11]孙志强, 项银杰, 张宏建. 差压式涡街质量流量计信号处理系统的研制[J]. 控制工程, 2007,14(增1): 185-188．

SUNZhi-qiang,XIANGYin-jie,ZHANGHong-jian.Developmentofsignalprocessingsystemfordifferentialpressuretypevortexmassflowmeter[J].ControlEngineeringofChina, 2007, 14(supple.1): 185-188．

[12]陆国生, 李立言, 赵民建. 全球导航卫星系统矢量载波环的设计与分析[J]. 浙江大学学报：工学版, 2015, 49(1): 20-26．

LUGuo-sheng,LILi-yan,ZHAOMin-jian.Designandanalysisofglobalnavigationsatellitesystemvectorcarrierloop[J].ZhejiangUniversity:EngineeringScience, 2015, 49(1): 20-26．

[13]PASETTOD,CAMPORESEM,PUTTIM.EnsembleKalmanfilterversusparticlefilterforaphysically-basedcoupledsurface-subsurfacemodel[J].AdvancesinWaterResources, 2012, 47: 1-13．

[14]LUS,ZHANGR.TwoefficientimplementationformsofunscentedKalmanfilter[J].ControlandIntelligentSystems, 2011, 39(1): 1-11．

[15]WANEA,VANDERMERWER.TheunscentedKalmanfilterfornonlinearestimation:adaptivesystemsforsignalprocessing,communications,andcontrolsymposium[C]∥AS-SPCC.LakeLouise:IEEE, 2000.

[16]徐德民, 刘富樯, 张立川, 等. 基于改进连续-离散无迹卡尔曼滤波的水下航行器故障诊断[J]. 西北工业大学学报, 2014(5): 756-760．

XUDe-min,LIUFu-qiang,ZHANGLi-chuan,etal.Faultdiagnosisofunderwatervehiclebasedonimprovedcontinuous-discreteunscentedKalmanfilter[J].JournalofNorthwesternPolytechnicalUniversity, 2014(5):756-760．

[17]梁丁文, 袁磊, 蔡之华, 等. 基于无迹卡尔曼滤波传感器信息融合的车辆导航算法[J]. 计算机应用, 2013, 33(12): 3444-3448．

LIANGDing-wen,YUANLei,CAIZhi-hua,etal.VehiclenavigationalgorithmbasedonunscentedKalmanfiltersensorinformationfusion[J].JournalofComputerApplications, 2013, 33(12): 3444-3448．

[18]江文斌, 秦会斌, 邵李焕, 等. 基于经典谱估计改进方法的涡街流量计[J]. 仪器仪表学报, 2012, 33(1): 229-234．

JIANGWen-bin,QINHui-bin,SHAOLi-huan,etal.Vortexflowmeterbasedonimprovedclassicalspectralestimation[J].ChineseJournalScientificInstrument, 2012, 33(1): 229-234．

[19]黄云志. 基于时频域分析的涡街流量计信号处理方法与系统的研究[D]. 合肥：合肥工业大学, 2005．

HUANGYun-zhi.Researchontimeandfrequencydomainbasedonsignalprocessingmethodsandsystemofvortexflowmeter[D].Hefei:HefeiUniversityofTechnology, 2005．

收稿日期：2015-06-08.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

作者简介：宋开臣(1965-),男,教授,博导,从事传感技术及仪器、现代测试技术及信号处理等研究.ORCID:0000-0003-4046-0004. E-mail: kcsong@zju.edu.cn 通信联系人：叶凌云,男,副教授.ORCID：0000-0002-3260-5157.E-mail: lyye@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.07.012

中图分类号：TH 814; TP 274

文献标志码：A

文章编号：1008-973X(2016)07-1307-06

Vortexsignalprocessingmethodbasedonmulti-sensorinformationfusion

SONGKai-chen,ZENGYao,YELing-yun

(College of Biomedical Engineering and Instrument Science, Zhejiang University, Hangzhou 310027, China)

Abstract:A vortex signal detection method based on multi-sensor information fusion was proposed in view of the poor anti-jamming performance of piezoelectric vortex flowmeter. In the measuring system, the average differential pressure before and after bluff body was measured by differential pressure pickup while the frequency of downstream vortex signal of bluff body by piezoelectric sensor. The two data above were fused by means of unscented Kalman filter (UKF), which effectively improved the locking precision of the digital band-pass filter. The feasibility of the method was verified through related experiments. The results of the method and the traditional method were comparatively analyzed. Experimental results show that the processing method can effectively restrain the impact of strong vibration noise interference from the outside on flow velocity measurement, which enhances the anti-vibration ability of piezoelectric vortex flowmeter and improves the flow measurement accuracy. When the vibration noise’s maximum intensity was four times stronger than the vortex signal, the measurement accuracy could achieve 1%．

Key words:piezoelectric vortex flowmeter; multi-sensor information fusion; unscented Kalman filter; anti-vibration ability