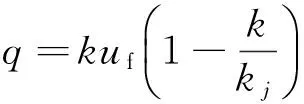基于状态可控性分析的交叉口信号切换控制

王　力,张立立,潘　科,李正熙

(北方工业大学 城市道路交通智能控制技术北京重点实验室,北京 100144)



基于状态可控性分析的交叉口信号切换控制

王力,张立立,潘科,李正熙

(北方工业大学 城市道路交通智能控制技术北京重点实验室,北京 100144)

摘要:针对目前交叉口的交通状态不能完全反映信号控制情况的问题,提出采用可控性的概念对交叉口的控制状态进行判定.通过定义通过率和阻塞率的综合作用结果,能够利用排队长度界定交叉口是否可控,采用交通波理论对剩余排队进行分析量化可控状态,以可控状态为判断条件建立交叉口信号切换控制模型.在“可控状态”下利用清空策略对交叉口进行控制,在“不可控状态”下将交叉口总排队最小设为目标函数,采用遗传算法求解策略对交叉口进行控制,给出不同控制状态下的控制策略.对实际路口进行仿真验证.结果显示,利用所提方法可以快速对交叉口交通状态进行判定,针对各种状态选择适合的控制策略,保证了交叉口的控制效果,证明了该方法的可行性和有效性.

关键词：通过率；阻塞率；交叉口可控性；切换控制

切换控制系统是混杂动态系统中的重要类型.系统的连续动态由若干个子系统来描述,系统的离散动态用决定在某一时刻系统的连续动态由哪个子系统来刻画[1].目前,切换控制系统的主要研究方向包括切换控制系统的稳定性、切换控制系统的时效性和切换控制策略的有效性三方面[2].

不同状态下的交叉口信号控制通常采用不同的控制策略,控制策略之间的转换具有明显的切换控制特点.赵晓华等[3-4]建立两交叉口切换控制模型,通过相位组合方式将该模型转化为单交叉口形式,采用智能体与Q学习算法实现两交叉口的协调控制.何忠贺等[5-12]将切换服务系统应用到交叉口信号控制中,设计“带有服务时间上限的固定相序切换”服务策略,开展切换服务系统周期稳定性的研究.范立权等[13]通过分析城市快速路出入口匝道及辅路交叉口的交通流特性,利用混杂自动机原理建立交叉口混杂切换系统模型,并利用模糊逻辑的方法优化交叉口的切换顺序实现对快速路区域的协调控制.向伟铭等[14-17]通过将过饱和状态下的排队车辆消散问题抽象为一类离散事件切换系统的指数稳定性问题,将排队溢出问题视为该类系统的有界性问题,建立信号交叉口的离散时间切换系统模型,并采用Lyapunov函数方法分析信号交叉口的稳定性和有界性,给出排队消散的控制策略.

目前将切换控制应用于城市道路交通信号控制中的研究多集中在切换序列的研究上,而针对不同交通状态变换下控制策略的研究,即不同交通状态下的切换控制的研究相对较少,同时鉴于交叉口过饱和状态多是由于交通信号控制与交通流相互作用所致的情况,交通状态不能完全反映出交叉口的可控状态.本文提出交叉口可控性的概念,以控制状态为条件进行交叉口的切换控制,能够使得控制策略更加适合交叉口的信号控制.

1交叉口状态可控性分析

在经典控制理论中,将系统的能控性描述为：“考虑一个系统,输入和输出构成系统的外部变量,状态属于反映运动行为的系统内部变量.从物理直观性来看,能控性研究系统内部状态是否可由输入影响.”交通系统属于复杂的非线性系统,同时具有非线性、时变性等特点,应用经典控制理论难以准确地描述交通系统的运行机理.针对该问题,结合交通控制的特点,本文提出交叉口可控性的概念.

交叉口的可控性用来描述交叉口信号控制与交通流之间的变化关系.若交叉口不可控,则信号控制和交通流相互作用会引起交叉口车辆排队长度增加,且增加幅度持续变大,最终导致排队溢出；反之,若交叉口可控,则信号控制和交通流相互作用所引起的交叉口车辆排队的变化是在一定范围内的,不会导致排队溢出.

为了定量描述,引入通过率、阻塞率及其综合作用结果等对交叉口可控性进行详细分析.

1.1通过率、阻塞率及综合作用结果

当交叉口处于过饱和交通信号控制的过程中时,随着时间的推移,各相位顺序获得通行权,此时获得通行权的车辆能够通过交叉口继续行驶.对于这种由交通控制产生的车辆通行,将其描述为交叉口的车辆通过率.当该相位通行权结束时,若存在剩余排队的车辆,则这些车辆是交叉口阻塞的车辆.基于该描述,引入交叉口通过率的概念,如下：

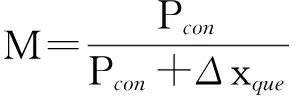
(1)

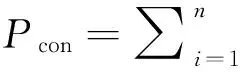
同理,将阻塞率用下式表示：

(2)

式中：N为交叉口的阻塞率,即剩余排队车辆数与总需求车辆数的比,N≤1.

如图1所示,交叉口的通过率和阻塞率是同时作用于交通信号控制过程中的.在交叉口处于过饱和的状态下,随着车辆排队的增加,交叉口的通过率逐渐降低,而交叉口的阻塞率逐渐增加,其中综合作用的结果可以用于描述交叉口的可控性.

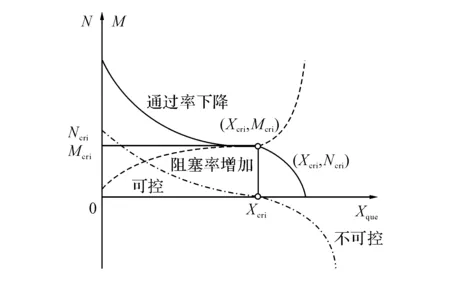
图1　交叉口通过率和阻塞率变化示意图Fig.1　Intersection through rate and blocking rate of change schematic diagram

由式(1)、(2),可得

R=M-N.

(3)

式中：R为交叉口车辆通过率和阻塞率的综合作用的结果,本文采用R对交叉口的可控性进行描述.在给定的周期条件下,在第K周期,若R<0,则交叉口的综合作用结果表现为车辆的阻塞率大于车辆通行率,假设输入流量保持不变或增大,交叉口的控制效果将持续变差,最终导致排队溢出,此时认为交叉口不可控；若R=0,则交叉口的综合作用结果表现为车辆的阻塞率等于车辆通行率,假设输入流量保持不变或减小,交叉口的控制效果不变或持续变好,此时认为交叉口可控；若R>0,则交叉口的综合作用结果表现为车辆的阻塞率小于车辆通行率,假设输入流量保持不变或减小,交叉口的控制效果不变或持续变好,最终排队消散,此时认为交叉口可控.

1.2基于交通波理论的剩余排队分析

对于上游稳定到达的流量q,从红灯启亮时刻考察路段排队的变化情况.根据交通波理论可知,两种交通状态相遇时产生的交通波的波速为u=(q1-q2)/(k1-k2).该波速为图2中两个状态对应的两个点相连形成的连线的斜率,如图2、3所示.

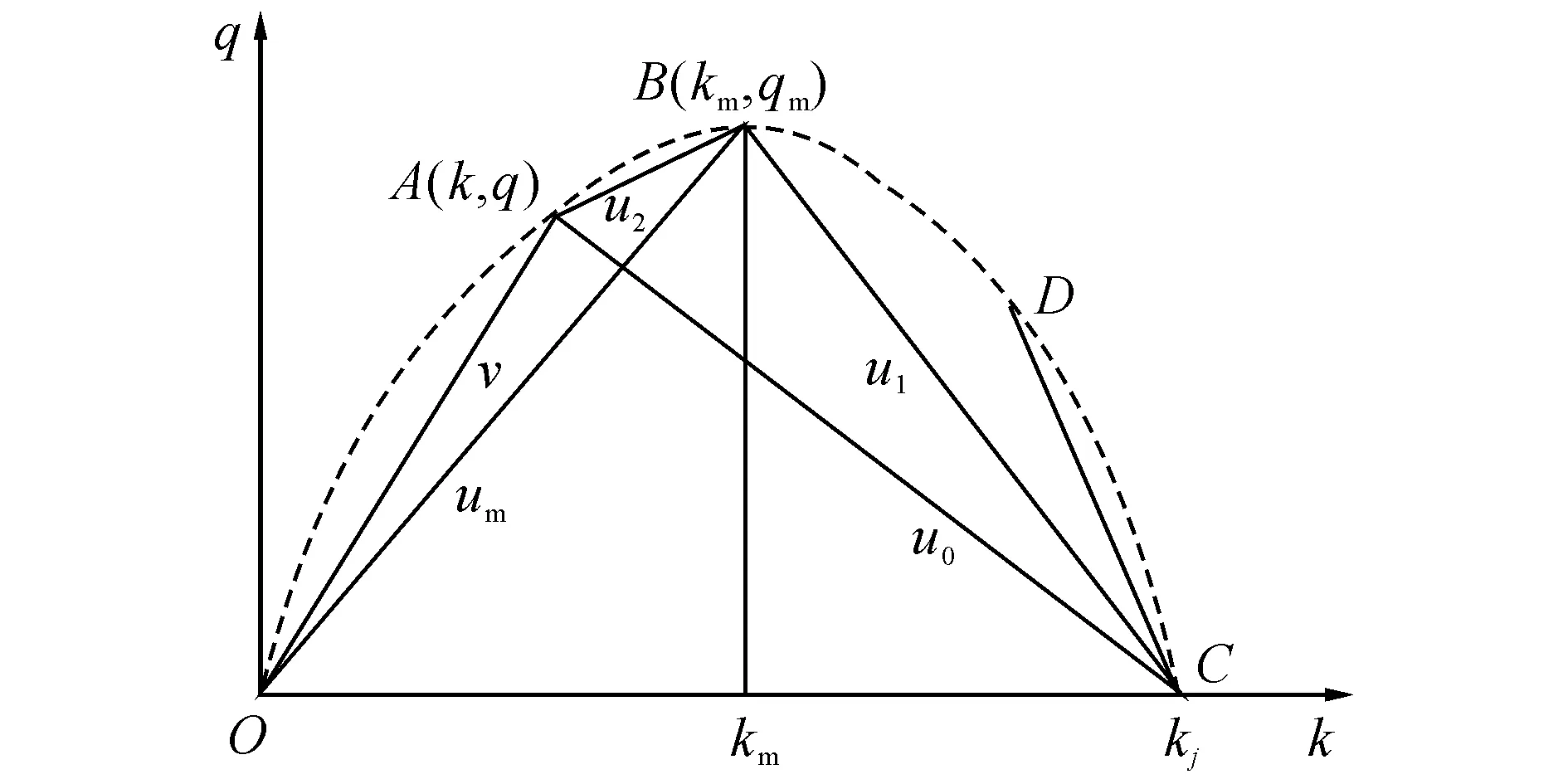
图2　流量-密度关系Fig.2　Flow-density relationship

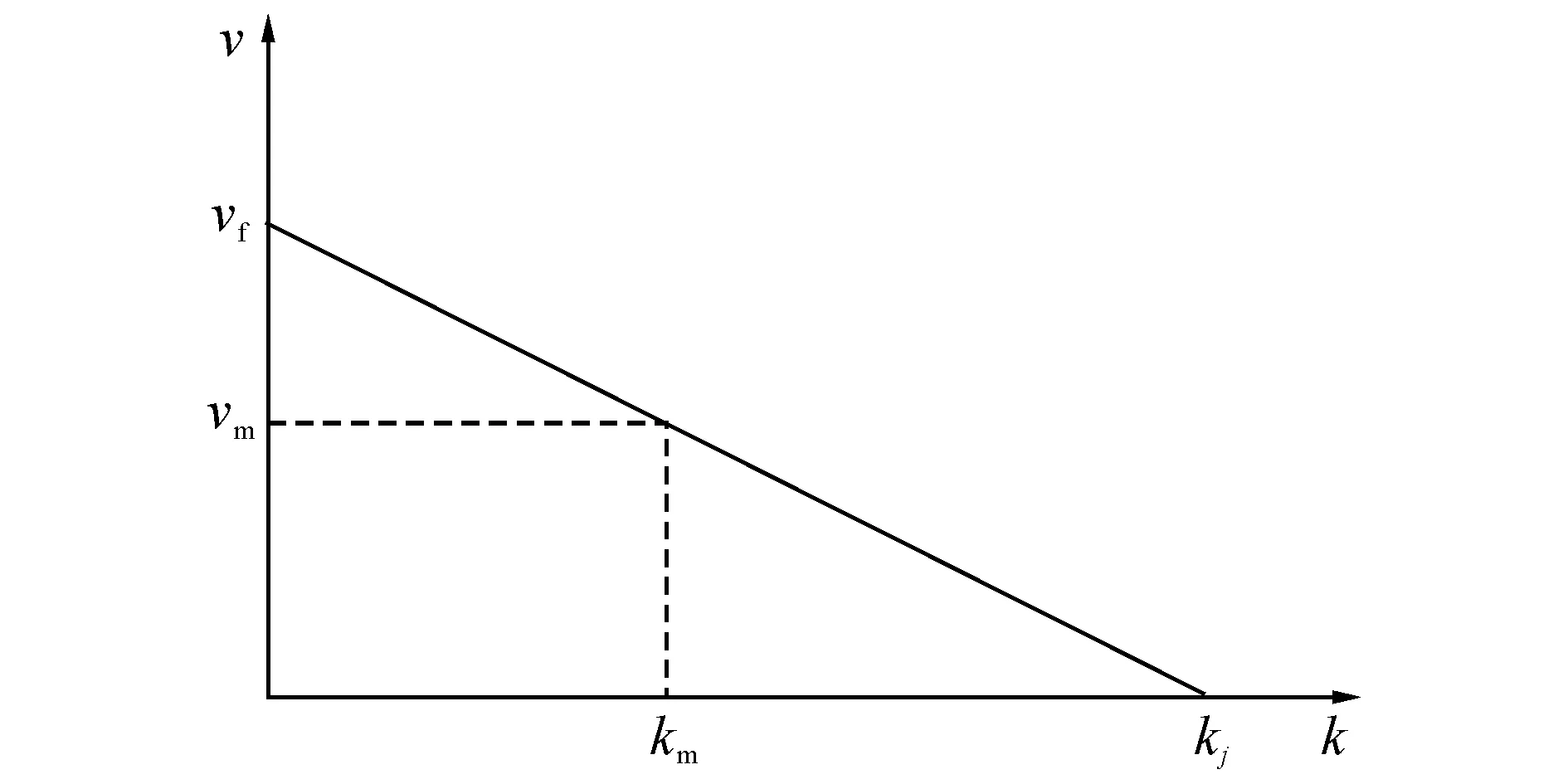
图3　速度-密度关系Fig.3　Speed-density relationship

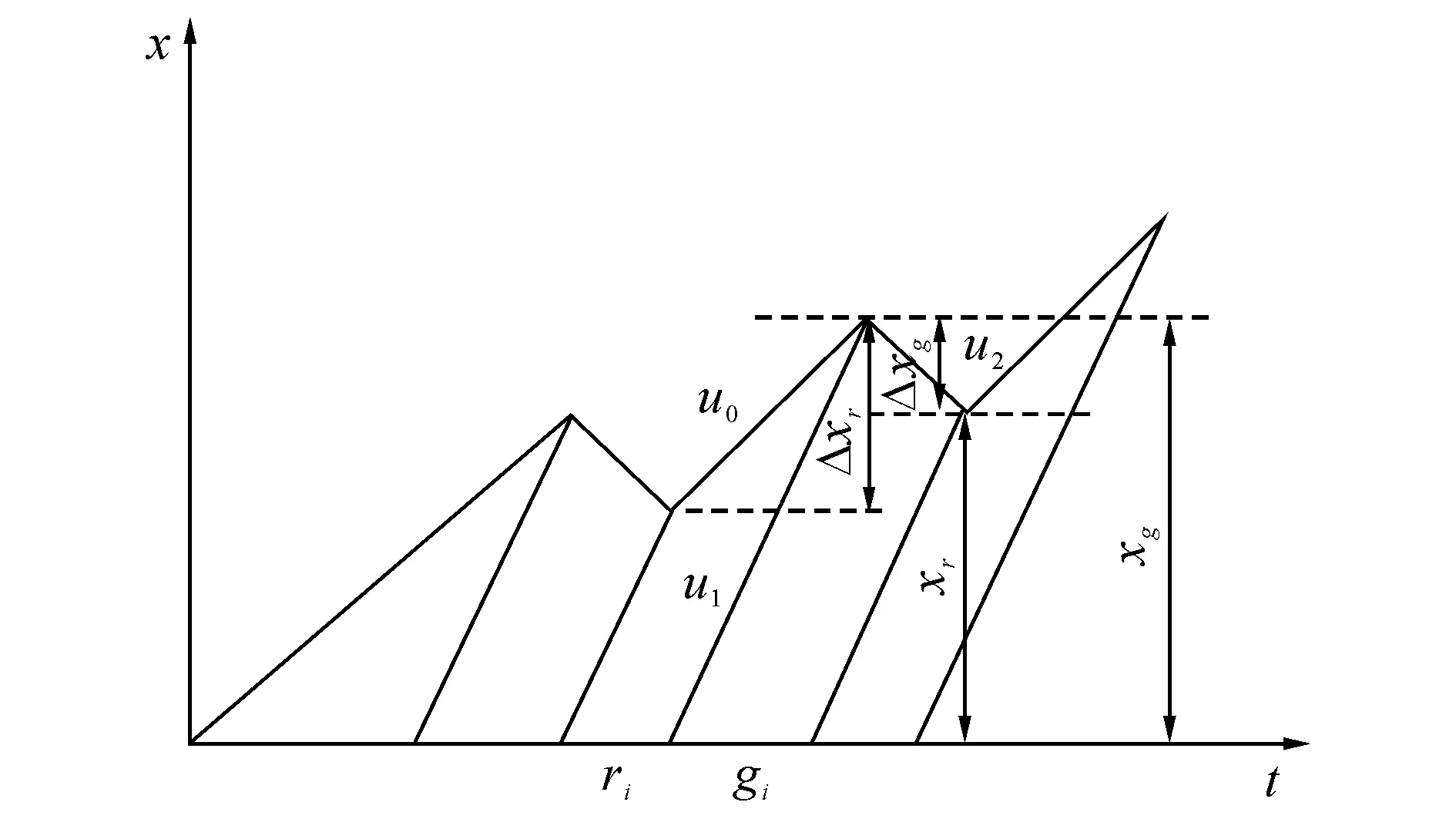
当红灯启亮时,产生一停车波向后传播,设波速为u0；当绿灯启亮时,产生一启动波,设波速为u1,经过时间t′,两个波相遇时,产生一新的交通波,将其表达为u2.该交通波向停车线方向传播,经过时间t″,波u2传至停车线,如图4所示.

由交通波理论可得各个交通波的波速如下：

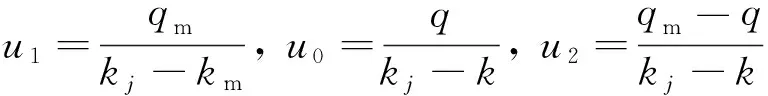
(4)

根据图4的几何关系,可将两个关键时间t′和t″推导出

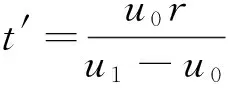
(5)

(6)

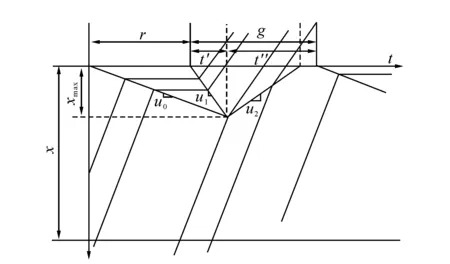
图4　交通波传播情况Fig.4　Traffic wave propagation

当绿灯时间g>t′+t″时,可以看出路段上的交通状态重复出现,因为状态是稳定的；当g=t′+t″时,路段处于临界状态,此时路段的状态是稳定的；当g

路段过饱和二次排队产生的临界条件如下：

(7)

由此可知,交叉口状态为欠饱和(指关键相位状态)是路段不发生过饱和二次排队的先决条件.当交叉口不满足临界条件时,排队逐渐向上游增加,如图5所示,在红灯期间车辆排队长度持续增长,而在绿灯时间排队长度逐渐缩短,其综合作用趋向于排队持续增加,交叉口相位增加的长度取决于流量和绿信比的关系.设ri结束时排队长度增加为Δxri,gi结束时排队长度缩短为Δxgi,从图5可得

(8)

当第i相位结束时,剩余排队：

(9)

图5　过饱和情况下的路段排队传播[9]Fig.5　Over-saturation in case of road queue spread

1.3交叉口状态可控性判据

由式(3)、(4)和(9)可得,交叉口的状态可控性可用下式描述：

(10)

式中：

qi(k)为第k周期相位i车辆到达流率；qm为最大流量；vm为最佳速度,即达到最大流量时的速度；km为最佳密度,即达到最大流量时的密度；ui为交通波波速；kj为阻塞密度；xmax为车辆最大排队长度；xri为ri结束时排队长度增加的值；xgi为gi结束时排队长度缩短的值；ri为相位i的红灯时间；gi为相位i的绿灯时间.

式(10)用于判断交叉口可控性的综合作用结果.在给定的周期条件下,在第K周期,若R<0,则交叉口的综合作用结果表现为车辆的阻塞率大于车辆通行率,假设输入流量保持不变或增大,交叉口的控制效果将持续变差,最终导致排队溢出,此时认为交叉口不可控；若R=0,则交叉口的综合作用结果表现为车辆的阻塞率等于车辆通行率,假设输入流量保持不变或减小,交叉口的控制效果不变或持续变好,此时认为交叉口可控；若R>0,则交叉口的综合作用结果表现为车辆的阻塞率小于车辆通行率,假设输入流量保持不变或减小,交叉口的控制效果不变或持续变好,最终排队消散,此时认为交叉口可控.

2基于状态可控性分析的交叉口切换控制

准确判断交叉口的可控性是实现交叉口切换控制的关键,而不同控制状态下的控制策略是交叉口正常运行、防治拥堵的保证.交叉口切换控制是指在不同控制状态下控制策略的切换.根据切换系统理论可知,控制策略的切换可以用有向图Y={Z,E}来表示,其中Z为控制策略的集合； E={R<0:zi,zj∈Y}为控制策略变迁(离散事件)的集合,R<0表示使控制策略mi变迁到mj的条件[20].

根据交叉口可控性可知,不同控制状态下的控制策略分为

Z={z1,z2}．

式中：z1为可控状态下的交叉口控制策略,z2为不可控状态下的交叉口控制策略.

交叉口控制策略的切换过程描述如下.在初始时刻t0,具有固定控制相序的交叉口,初始排队为xio,控制策略为z1,在切换条件R<0发生之前,遵循“可控状态”下的交叉口控制策略z1；在t1时刻,切换条件R<0发生,控制策略变迁为z2,即切换条件R<0的发生导致控制策略从z1变迁为z2,此后交叉口将遵循“不可控状态”下的交叉口控制策略z2,并且该切换过程随着切换条件的变化而动态变化.控制策略的切换过程可以用图6表示.

图6　交叉口切换控制过程Fig.6　Intersection switching control process

2.1切换控制规则描述

交叉口控制策略的切换规则采用自动机的方法,通过判断交叉口的可控性来决定交叉口应该处于哪种控制策略.具体的切换规则如下.

1)对交叉口交通状态进行判断,若交叉口处于欠饱和状态,则交叉口采用“可控状态”下的控制策略；若交叉口处于过饱和状态,则继续判断交叉口的控制状态.

2)对交叉口的控制状态进行判断,若交叉口处于“可控状态”,即R>0,则交叉口采用“可控状态”下的控制策略；若交叉口处于“不可控状态”, 即R<0,则将当前运行周期设置为过渡周期,并判断过渡周期是否结束.当过渡周期结束时,采用“不可控状态”下的控制策略.

3)对于交叉口控制状态的判别,一个运行周期内只进行一次判断.

如图7所示为交叉口切换控制流程图.

图7　切换控制流程图Fig.7　Switching control flowchart

2.2“可控状态”下交叉口控制策略

针对上述所设计切换控制中的“可控状态”,采用如下控制策略.

1)当交叉口处于可控状态时,可以采用该控制策略,其中交叉口处于可控状态是采用该控制策略的充分必要条件.

2)设交叉口的控制相位个数为n,相位1首先获得通行权,相序为1→2…→n→1|n≥2(任意固定相序均可).

3)当相位i获得通行权, 且其内车流被清空xi(k)=0时, 相位切换到下一相位i+1, i=1,…,n-1|n≥2；当相位n获得通行权, 且其内车流被清空xn(k)=0, 相位重新切换到相位1.

4)当相位i获得通行权时,有效绿灯满足：

(11)

若

i=1,2,…,n|n≥2,

则有

式中：gci为采用Webster计算的初始相位绿灯时间,gi(k)为第k周期相位i获得的绿灯时间,li(i+1)为相位i和相位i+1之间的过渡时间.

5)当相位i切换到相位i+1时, 相位损失时间为li(i+1)>0,i=1,…,n-1|n≥2; 当相位n切换到相位1时, 相位损失时间为ln1．

2.3“不可控状态”下交叉口控制策略

针对上述切换控制模型中的“不可控状态”,采用如下控制策略.

1)当交叉口处于不可控状态时,可以采用该控制策略,其中交叉口处于不可控状态是采用本控制策略的充分必要条件.

2)处于不可控状态下的交叉口主要参数有如下关系：

(12)

(13)

由式(12)、(13)可得

Qi(k)=Pi(k).

(14)

式中：Qi(k)表示第k周期相位i的通行能力,Pi(k)表示第k周期相位i的单位时间内放行的车辆.

(15)

因此有

令

则有

(16)

设在第k周期各相位均有初始排队xio(k),则交叉口第k周期内总排队为

(17)

式中： xio(k)表示第k周期相位i的初始排队的车辆.

3)采用遗传算法进行优化.

a)相位1首先获得通行权, 相序为1→2…→n→1|n≥2(任意固定相序均可).

b)将周期内交叉口各相位总排队车辆数最小设置为目标函数：

(18)

式(18)满足约束条件：

(19)

c)设置适应度函数为

(20)

d)设计包括种群规模、交叉概率、变异概率、优化代数等.

3实例验证

3.1对比验证

设计如表1所示的数据对两相位控制交叉口采取不同控制方式(定时控制和本文切换控制,其中仿真参数设置的交通环境相同)的控制效果进行验证,并对仿真结果进行分析.表中，Na、Eb分别为北进口和东进口流量.

表1　两相位控制交叉口各相位流量数据

1) 数据组1仿真结果.

图8中，N为北进口排队车辆数，E为东进口排队车辆数.如图8所示,选取的数据为交叉口在“可控状态”之间过渡(即“可控”和到“可控”).在欠饱和状态下,带有初始排队的交叉口各相位在一定时间,排队逐渐减小最终达到排队稳定状态,其中定时控制下交叉口总排队长度大于所提切换控制下交叉口的总排队长度.

图8　欠饱和下不同控制策略相位排队Fig.8　Under-saturated under different control strategies phase queue

2) 数据组2仿真结果.

图9　过饱和下不同控制策略相位排队Fig.9　Over-saturated under different control strategies phase queue

如图9所示,选取的数据为交叉口在“不可控状态”之间过渡(即“不可控”和到“不可控”).可以看出,在过饱和状态下各种控制策略都不能对交叉口进行有效控制,采用提出的切换控制减缓了交叉口控制过程中交叉口总排队长度的增加趋势.

3) 数据组3仿真结果.

图10　不同控制状态下各控制策略相位排队 Fig.10　Different control status of each control strategy of phase queue

如图10所示,选取的数据为交叉口在“可控状态”和“不可控状态”之间过渡(即“可控”和到“不可控”,“不可控”和到“可控”).在不同的交叉口变换过程中,提出的切换控制在交叉口控制中能够有效地减小各相位总排队长度,尤其是交叉口从“不可控状态”转向“可控状态”时优势更加明显.

3.2实例验证

为了验证所提切换控制的优劣,选取北京市交通学院南路和交大东路交叉口东西和南北两相位的交通数据进行仿真验证.该交叉口2个方向5:00～21:00的交通流数据如图11所示(每15 min采集一次,折合成小汽车当量).图中，K为关键入口车流量.

如图12所示,交叉口存在初始排队,在开始阶段由于交叉口处于“可控”状态,各相位排队长度逐渐减小直到稳定；在一段时间后由于各相位的流量增加,交叉口从“可控”转向“不可控”,此时相位排队逐渐增加,交叉口重复出现前述过程.从图12可以看出,当交叉口处于“可控状态”时,各种控制策略均能够进行有效控制,当交叉口切换至“不可控状态”时,本文所提切换控制能够使得交叉口各相位的排队总和达到最小,从而使得交叉口在“不可控状态”下得到有效控制.交叉口在不同状态下的转换过程中,采用所提切换控制使得各相位的排队变化幅度最小,避免出现排队大幅振荡的现象.

图11　交通学院南路和交大东路交叉口交通流量Fig.11　Traffic school south road and jiaoda road intersection traffic flow

图12 不同控制策略下交叉口各相位排队Fig.12　Different control strategies of each intersection of phase queue

4结语

在分析交叉口控制状态的基础上引入通过率和阻塞率,利用综合作用结果定义交叉口的可控性.通过采用交通波理论分析交叉口相位剩余排队,使得到的综合作用结果更符合交通的实际状况,从而更好地反映出交叉口可控性的真实面目.将交叉口可控性作为切换条件,建立切换控制模型,通过在“可控状态”下利用清空策略对交叉口进行相应控制,在“不可控状态”下将交叉口最小总排队设为目标函数,采用遗传算法进行求解的方式对交叉口进行控制,从而得到适应不同状态的交叉口的控制策略.

参考文献(References):

[1]付俊. 非线性级联系统的鲁棒不变切换控制[D]. 沈阳：东北大学,2004．

FU Jun. Robust invariance switching control for nonlinear cascade systems [D]. Shenyang: Northeastern University, 2004．

[2]方志明. 切换系统稳定性分析与优化控制若干问题研究[D]. 南京：南京理工大学,2012．

FANG Zhi-ming. Study on several problems of stability and optimal control of switched systems [D]. Nanjing: Nanjing University of Science and Technology, 2012．

[3]赵晓华,李振龙,于泉,等. 基于切换模型的两交叉口信号灯Q学习协调控制[J]. 北京工业大学学报,2007, 33(11): 1148-1152．

ZHAO Xiao-hua, LI Zhen-long, YU Quan, et al. Based on switching-model cooperative control for two intersection applying Q-learing [J]. Journal of Beijing University of Technology, 2007, 33(11): 1148-1152．

[4]赵晓华, 陈阳舟. 基于混杂系统理论的单交叉口信号灯控制[J]. 北京工业大学学报, 2004, 30(4): 412-416．

ZHAO Xiao-hua, CHEN Yang-zhou. Traffic light control method for a single intersection based on hybrid systems theory [J]. Journal of Beijing University of Technology, 2004, 30(4): 412-416．

[5]何忠贺,陈阳舟,石建军. 切换服务系统的稳定性及交叉口信号配时[J]. 控制理论与应用,2013, 30(2): 194-200．

HE Zhong-he, CHEN Yang-zhou, SHI Jian-jun. Stability of switched server system and signal timing of intersection [J]. Control Theory and Applications, 2013, 30(2): 194-200．

[6]何忠贺. 切换服务网络的稳定性及交通信号控制应用[D]. 北京：北京工业大学,2013．

HE Zhong-he. Stability of switched server network and ITS application in traffic signal control [D]. Beijing: Beijing University of Technology, 2013．

[7]HE Zhong-he, CHEN Yang-zhou, SHI Jian-jun, et al. Stability of switched server systems with finite buffer capacity[C]∥Control Conference (CCC). [s.l.] IEEE, 2013: 2108-2113．

[8]HE Zhong-he, CHEN Yang-zhou, SHI Jian-jun, et al. Steady-state control for signalized intersections modeled as switched server system[C]∥American Control Conference (ACC). [s.l.]: IEEE, 2013: 842-847．

[9]HE Zhong-he, WANG Li, ZHANG Li-li. Controllability of switched server systems with service-time and queue constraints on buffers[C]∥Control Conference (CCC). [s.l.]: IEEE, 2015: 140-145．

[10]WANG Li, HE Zhong-he, ZHANG Chi, et al. Stability of switched server systems with constraints on service-time and capacity of buffers[J]. Mathematical Problems in Engineering, 2015, 2015: 1．

[11]CHEN Yang-zhou, ZHANG Ya-xiao, HE Zhong-he, et al. Average dwell-time conditions of switching information topologies for consensus of linear multi-agent systems[C]∥Control Conference (CCC).[s.l.]. IEEE, 2013: 7115-7120．

[12]CHEN Yang-zhou, HE Zhong-he, YU A. Existence of common lyapunov function based on KKM lemma for switched Persidskii-type systems[C]∥2011 International Conference on Electric Information and Control Engineering (ICEICE). [s.l.]: IEEE, 2011: 371-374．

[13]范立权,陈阳舟,李振龙. 基于混杂模糊切换的快速路区域协调控制[J]. 交通信息与安全,2009, 27(3): 44-48．

FAN Li-quan, CHEN Yang-zhou, LI Zhen-long. Freeway area-wide coordinated control based on hybrid system and fuzzy switch [J]. Journal of Transportation Information and Safety, 2009, 27(3): 44-48．

[14]向伟铭. 基于切换系统理论的混杂交通系统特性分析[D]. 成都：西南交通大学, 2014．

XIANG Wei-ming. Characteristic analysis for hybrid transportation system based on switched system theory [D]. Chengdu:Southwest Jiaotong University, 2014．

[15]向伟铭,肖建,蒋阳升. 基于切换系统的过饱和信号交叉口混杂控制[J]. 交通运输系统工程与信息,2014, 14(2): 57-61．

XIANG Wei-ming, XIAO Jian, JIANG Yang-sheng. Hybrid control for over-saturated signalized intersection based on switched system [J]. Journal of Transportation on Systems Engineering and Information Technology, 2014, 14(2): 57-61．

[16]XIANG Wei-ming, XIAO Jian. Real-time signalization for an oversaturated intersection via switched system approach[C]∥Control Conference (CCC). [s.l.]:IEEE, 2014: 3350-3355．

[17] XIANG Wei-ming, XIAO Jian, IQBAL M N. State estimation for short-time switched linear systems under asynchronous switching [J]. International Journal of Adaptive Control and Signal Processing, 2014, 28(6): 553-561．

[18]祁宏生. 考虑信号控制的路网交通流建模[D]. 长春：吉林大学,2011．

QI Hong-sheng. Research on the modelling of network traffic flow considering signal control [D]. Changchun: Jilin University, 2011．

[19]QI Hong-sheng, WANG Dian-hai, SONG Xian-min. On the critical conditions of traffic jams [J]. Journal of Southeast University (English Edition), 2011, 27(2): 180-184．

[20]汪少华,陈龙,孙晓强. 半主动空气悬架多模式切换控制模型的分析[J]. 江苏大学学报：自然科学版,2013, 34(6): 637-642．

WANG Shao-hua, CHEN Long, SUN Xiao-qiang. A multi-mode switching control mode for semi-active air suspension [J]. Journal of Jiangsu University: Natural Science Edition, 2013, 34(6): 637-642.

收稿日期：2015-06-17.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(51308005)；科研基地建设-首都世界城市顺畅交通协同创新中心-参与单位(2011协同)(市级)资助项目(PXM2014_014212_000020)；学科建设-国家特殊需求-城市道路交通智能控制人才培养资助项目(PXM2014_014212_000053)；研究生培养-研究生教育-产学研联合培养研究生基地(市级)资助项目(PXM2014_014212_000032).

作者简介：王力(1978-)，男，副教授，从事智能交通信号控制系统、交通大数据分析的研究.ORCID:0000-0001-6718-0737. E-mail:wangli939@ncut.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.07.007

中图分类号：U 491

文献标志码：A

文章编号：1008-973X(2016)07-1266-10

Traffic signal switching control approach based on state control ability analysis

WANG Li,ZHANG Li-li,PAN Ke,LI Zheng-xi

(IntelligentTransportationKeyLaboratory,NorthChinaUniversityofTechnology,Beijing100144,China)

Abstract:Judging the traffic condition of intersection using the concept of “controllability” was proposed aiming at the problem of existing methods that judge traffic states can’t fully reflect the traffic condition of the intersection. The length of the queue can be utilized by blocking rate defined by the rate and the result of the combined effect in order to define if intersection can be controlled. The traffic wave theory analysis was conducted to quantify the remaining queue for controllable state. The switching control model of intersection was established by using the controllable state as the judgment condition. In the “controllable state”, the policy was used to take advantage of empty intersection control. In the “uncontrollable state”, the intersection minimum objective function was set by using genetic algorithm strategy intersection control. Control strategy under different control state was given. A real network was selected to conduct a simulation. Results show that using the proposed method of intersection traffic state can quickly be determined. The appropriate control strategy was selected for a variety of state. Then the control effect of the intersection was ensured. The feasibility and effectiveness of the proposed method were proved．

Key words:through rate; block rate; intersection controllability; switching control