Benders算法在发电机无功储备管理中的应用

李 杰，罗滇生，李帅虎，吴迎昌（湖南大学电气与信息工程学院，长沙 410082）

Benders算法在发电机无功储备管理中的应用

李 杰，罗滇生，李帅虎，吴迎昌
（湖南大学电气与信息工程学院，长沙 410082）

摘要：电力系统的电压稳定性与系统中的无功储备密切相关。首先，建立了考虑N-1预想故障静态安全约束的发电机无功储备管理模型，并利用Benders算法将该模型分解为一个与正常运行方式相关的主问题和一系列与预想故障相关的子问题：主问题处理正常运行方式下的相关约束以及子问题所返回的Benders割约束，子问题处理一系列的预想故障及静态安全约束。其次，为提高Benders分解算法的求解效率，进一步提出了一种结合连续潮流方法的并行求解策略，减少了所需求解子问题的个数，仅返回一个Benders割至主问题。以IEEE 39节点系统作为算例，仿真结果验证了本文所提模型的正确性及求解策略的有效性。

关键词：电力系统；静态安全约束；无功储备；Benders算法；预想故障

国内外近期发生的失稳事故机理分析表明，无功不足是导致电压失稳的一个关键因素，因而维持一定的无功储备对提高电力系统暂态稳定性的支撑能力至关重要［1-3］。传统的电力系统无功源主要包括发电机、同步调相机、静止无功补偿器SVC （static var compensator）/静止同步补偿器STAT⁃COM（static synchronous compensator）和并联电容补偿器。考虑到发电机是目前系统中最主要的无功源且其控制成本低廉，因此如何更实际有效地实现对发电机无功储备的优化管理，一直以来是电力研究者们的关注重点［3-9］。

发电机无功储备优化管理的主要目标是保证系统在各种运行方式下具有足够的电压稳定裕度。对发电机无功储备的优化管理，理论上需考虑正常运行方式、负荷水平变化、元件的N-1开断和部分重要元件多重开断的情况。考虑到多场景下研究的复杂性，现有的发电机无功储备优化管理主要针对正常运行方式和负荷水平变化的情况，在满足元件运行约束和系统期望的电压稳定裕度要求条件下，最大化发电机的无功储备，提高系统的电压稳定裕度［4-10］。文献［4-5］提出在满足系统正常运行方式相关约束的条件下，最小化发电机的无功出力（等价于无功储备最大）来提高系统的电压稳定性。文献［6-8］在无功储备的优化管理中考虑了系统在基态运行方式及重负荷水平下的相关约束。文献［9-10］提出了考虑系统处于最大运行方式下的无功储备管理方法，通过最小化当前运行方式下的无功出力，最大化系统处于最大运行方式时的无功出力来提高系统的电压稳定性。

但上述方法都未考虑系统N-1预想故障方式下的发电机无功储备管理问题。2003年，意大利大停电正是由于未考虑重要输电线路跳闸，频率下降，导致发电机低频保护动作而退出运行，造成事故影响扩大［11］，其主要原因是系统中缺乏足够的无功储备来保证系统发生N-1故障时的电压稳定。因此，无功储备管理研究中考虑系统N-1故障下的场景更有利于避免连锁故障导致的大停电事故发生。

基于上述理论，本文建立了考虑N-1预想故障静态安全约束的无功储备优化管理模型。结合连续潮流方法的并行求解策略，有效地克服了串行求解策略中出现的“振荡”现象，在不影响计算结果精度的同时提高了问题的求解效率。算例仿真充分说明了本文所提无功储备管理模型的正确性和求解策略的有效性。

1 无功储备优化管理模型

本文所提发电机无功储备管理模型可以描述为：在满足系统正常运行方式及N-1预想故障静态安全约束的前提下，通过对发电机无功备用的优化管理，最大化系统的无功储备。在正常运行状态下，若系统发生预想故障，可不采取任何新的控制措施仍使系统具有期望的静态电压稳定裕度，同时增加系统的无功储备，从而提高系统的电压稳定性。

发电机的过励保护是影响其无功出力的一个重要因数；稳态下发电机的无功出力与基端电压及其限值、发电机的有功出力、电厂辅机母线电压等因数也密切相关［12］。鉴于上述情况较为复杂，在静态电压稳定分析中，本文以可持续的发电机励磁水平所对应的无功储备作为研究对象，将发电机的无功出力限值用简单的固定值表示。

本文提出的发电机无功储备优化管理模型为

式中：QGi，res为发电机的无功储备，在某些情况下，发电机无功出力也可能减小，因此吸收无功的能力也是一种储备［12-13］；QGi、QGi，max分别为发电机i无功出力和最大无功出力；SR为系统发电机节点集合；p1为发电机i的权值；当p2＜0时，表示系统有功损耗的权值；Ploss为系统的有功损耗。

1.1 正常运行方式静态电压稳定约束

正常运行方式潮流平衡方程约束为

式中：SB为网络节点总数；Y0为系统正常运行方式网络节点导纳矩阵；U0为正常运行方式下节点电压幅值向量；θ0为正常运行方式下相角向量；λ0为负荷增长因子，表示正常运行方式下系统所期望获得的静态电压稳定裕度；P和Q为正常运行方式下注入节点i的有功功率和无功功率；P和Q为正常运行方式下节点i的有功负荷和无功负荷。

正常运行方式下节点电压上、下限约束和节点无功注入约束分别为

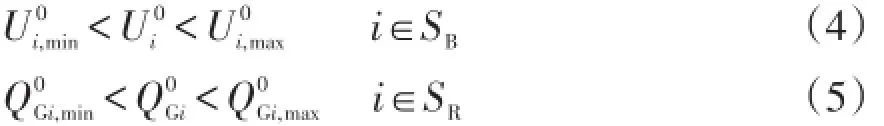
i无功出力的最大值和最小值。

1.2 N-1预想故障下静态电压稳定约束

预想故障下的潮流平衡方程约束为

式中：Yp为预想故障p下网络节点导纳矩阵；Up为预想故障p下节点电压幅值向量；θp为预想故障方式p下的相角向量；λp为负荷增长因子，表示预想故障p下系统所期望获得的静态电压稳定裕度。

预想故障下节点电压上、下限约束和节点无功注入约束分别为

当系统规模较大时，所需考虑的N-1预想故障集数量庞大，系统在各预想故障下所需满足的静态安全约束直接导致计算量非常大。针对该问题，本文后续提出采用Benders分解算法使得该问题得到有效的处理。

2 基于Benders算法的无功储备管理

基于Benders算法，发电机无功储备优化管理模型可以分解为具有循环迭代机制的主问题和子问题［14-15］。其中主问题处理正常运行方式相关约束及由子问题返回的Benders割，子问题处理各预想故障及相应的静态安全约束。将主问题的求解所获得的控制变量以已知量的形式代入所有子问题进行子问题的求解，若某个子问题不能满足相关约束则以Benders割的形式返回主问题，继续主问题的求解，从而产生新一轮的无功控制变量组合，继续上述迭代过程（见图1）。构造相应的主问题与子问题模型，关键在于建立合理有效的Benders割，将子问题得出的信息反馈给主问题。

图1 Benders分解结构Fig.1 Structure of Benders decomposition

2.1 子问题模型

根据Benders算法原理，针对上述考虑正常运行状态及预想故障下静态安全约束的最优潮流问题，将每个预想故障形成一个独立的子问题，第k轮迭代中子问题p的模型可以描述为

式中：sci、sri为松弛变量，表示节点功率不平衡量；u为第k轮迭代中求解主问题所获得的控制变量，以已知量的形式代入子问题进行子问题的求解。松弛变量的作用在于当主问题获得的无功控制变量u（包括PV发电机的机端电压UPV和PQ发电机的无功输出QPQ）不能保证子问题p所期望的静态电压稳定裕度时，有效缓解这一现象，保证子问题始终有解。

在子问题的模型中，若由主问题计算得到的控制变量u使得子问题的目标函数Sk（u）=0，则表明预想故障p发生后在不采取新的控制措施条件下系统能够获得期望的静态电压稳定裕度；若Sk（u）＞0，则说明其不能满足子问题p的静态安全约束，此时将子问题的求解获得的相关信息返回主问题形成Benders割，进而修正下一轮无功控制变量优化结果。所有不能满足静态电压稳定裕度要求的子问题都需要向主问题返回相应的Benders割进行迭代计算，直至所有子问题均不发生越界。

2.2 主问题模型

将越界子问题所得出的信息反馈到主问题形成Benders割约束，反映子问题对主问题的影响。主问题的模型包括式（1）～（5）和Benders割约束，其约束形式为

式中：uk+1为第k+1轮迭代待优化的无功控制变量，在主问题的第1轮迭代过程中不包含Benders割表示的静态安全约束；φk为第k轮迭代中求解子问题获得的与式（17）相对应的最优拉格朗日乘子。

3 结合连续潮流方法的并行求解策略

对于实际电力系统，N-1预想故障数量庞大，大量的子问题及返回到主问题的Benders割约束将导致问题的求解异常繁琐。本文采用文献［16］所提的“不诚实”并行求解策略，并结合连续潮流方法，每次迭代时先用连续潮流方法对预想故障进行扫描，将不能满足系统电压稳定裕度要求的预想故障作为待求的子问题。不需要对所有预想故障都进行计算，减少所需求解的子问题个数。然后分别取各越界子问题返回的矢量S（u）和φ的平均值来形成主问题的单一Benders割约束，避免了主问题中出现多个Benders割约束，提高了求解效率。具体求解流程如下。

（1）数据初始化。读入系统相关数据。φk=0；Sk（u）=0；k=0；kmax=10，表示最大迭代次数。

（2）计算正常运行方式主问题。求解主问题控制变量uk，得到发电机的最大无功储备及系统的有功损耗（k=0）。

（3）用连续潮流方法对各预想故障进行扫描。若所有子问题均满足系统所期望的电压稳定裕度要求，各节点电压不越限，则输出uk为最优解，求得相应的发电机无功储备及系统的有功损耗，直接转步骤（7）；否则转步骤（4）。

（4）利用“不诚实”并行求解策略求解各越界子问题。得到各子问题最优解的平均值S~（u）和最优拉格朗日乘子的平均值φ~（u），形成单一的Benders割返回主问题。

（5）重新求解含Benders割约束的主问题。获得uk+1及系统的最大无功储备和系统的有功损耗（k=k+1）。

（6）用连续潮流方法对各预想故障进行扫描。若各预想故障均能满足系统预定的电压稳定裕度要求转步骤（7）；否则，转步骤（4）。

（7）迭代结束。

4 算例分析

本文将提出的发电机无功管理模型应用到IEEE 39节点系统进行仿真分析。该系统包括10台发电机，12台变压器和34条传输线路，系统的基本参数参见文献［17］。正常运行方式下及N-1预想故障下系统期望的静态电压稳定裕度分别取15%、10%；各节点电压约束上、下限分别取0.92、1.08。主、子问题均采用原-对偶内点法进行求解，收敛精度ε=1×10-6。

4.1 结合连续潮流方法的并行求解策略计算过程

根据算法流程进行第1轮迭代。首先求解不含Benders割约束的主问题，发现当线路14-15故障时，发电机G32吸收的无功功率为8.429 Mvar，同时得到发电机的无功储备为1 601.21 Mvar，系统的有功损耗为40.83 MW。再利用连续潮流方法对各预想故障进行扫描，发现有5条线路发生断线故障后不能满足系统期望的电压稳定裕度要求，分别为线路6-11、2-25、8-9、26-27和21-22。结果如表1所示。

表1 第1轮迭代计算结果Tab.1 Calculation results of the first round iteration

以这5个故障构成子问题，通过并行求解策略进行计算，计算得5个子问题的目标函数的平均值S~（u）=4.71，形成单一的Benders割返回主问题，进行第2轮计算。第2轮迭代过程中，首先计算含有Benders割约束的主问题，得出发电机的无功储备为1 577.14 Mvar，较第1轮计算时有所减小，系统的有功损耗为41.01 MW，较第1轮计算时大，这是由于系统的无功出力增大而导致线路的有功损耗增加。采用连续潮流方法对预想故障进行扫描，此时线路2-25、6-11发生断线故障后的系统电压稳定裕度为10.323%、10.433%，均能满足故障后10%的裕度要求，且另外3个故障下系统的电压稳定裕度都有所改善。计算结果如表2所示。

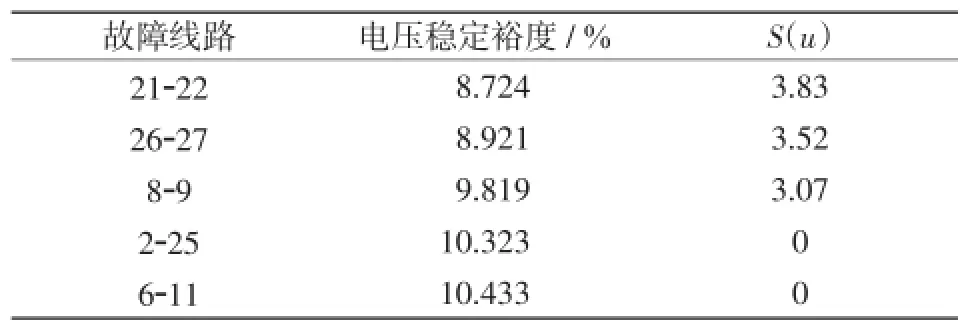
表2 第2轮迭代计算结果Tab.2 Calculation results of the second round iteration

以故障21-22、26-27、8-9构成子问题进行求解，计算得S~（u）=3.47，返回Benders割至主问题，进行第3轮迭代计算。求得发电机的无功储备为1 543.63 Mvar，系统的有功损耗为41.22 MW。对控制变量进行更新，利用最优潮流法扫描各预想故障，线路26-27、8-9、2-25、6-11断线后系统的电压稳定裕度分别为10.121%、10.147%、10.425%、10.651%，均大于10%，仅线路21-22发生故障后不能满足10%的裕度要求。计算结果如表3所示。

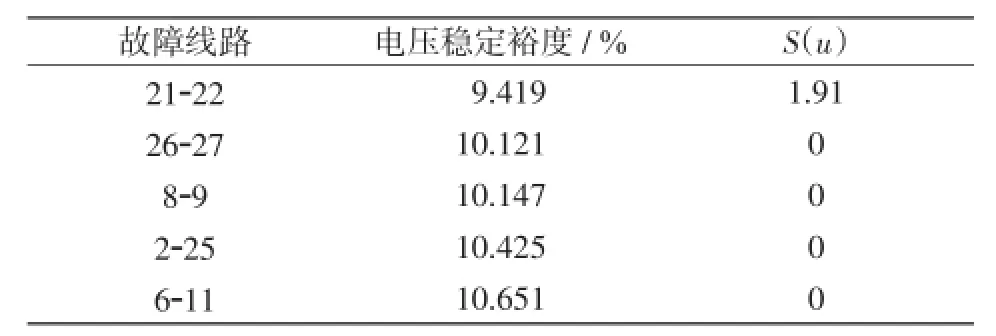
表3 第3轮迭代计算结果Tab.3 Calculation results of the third round iteration

选择故障线路21-22作为子问题求解，计算得S~（u）=1.91，返回Benders割至主问题，进行第3轮迭代计算。求得发电机的无功储备为1 507.92 Mvar，系统的有功损耗为41.36 MW。利用最优潮流法扫描各预想故障，发现所有预想故障均满足系统所期望的静态电压稳定裕度要求，计算结束。

4.2 考虑与不考虑预想故障计算结果比较

由表4可以看出：不考虑预想故障下发电机的无功储备为1 601.21 Mvar（由第1轮迭代求解主问题获得），较考虑预想故障后发电机的无功储备（1 507.92 Mvar）乐观，因此在无功储备的优化管理过程当中必须考虑预想故障的影响；由于预想故障下系统的无功出力较前者大，因此有功损耗也相对较大。

表4 两种计算方式结果比较Tab.4 Comparison of results between two different ways

4.3 3种计算策略的比较

本文分别利用3种计算策略对该模型进行计算：①并行计算，计算结果由第4.1节给出；②串行计算，即在每次的迭代过程中选用最严重的故障作为待求的子问题；③直接计算，即将所得所有的Benders割加入主问题。表5给出了采用串行计算策略求解该问题时的目标函数值，表6为3种计算策略的比较。

表5 采用串行计算策略时子问题的目标函数值Tab.5 Values of objective function of the subproblem using serial calculation strategy

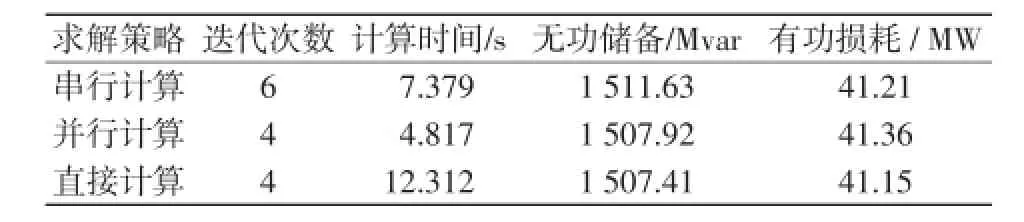
表6 3种计算策略的比较Tab.6 Comparison of results among three different calculation strategies

从表5、6可以看出：采用串行求解策略的计算过程中，子问题的目标函数值S（u）出现了“振荡”现象，即第4轮迭代过程中子问题的目标函数值S（u）较第3轮大，需要6轮迭代求解才能获得问题的最优解。从计算时间来看，采用并行求解策略的计算时间为4.817 s，计算速度最快；从计算结果来看，3种求解策略计算结果的精度差别不大。

5 结语

本文以最优潮流为基础，建立了一种发电机无功储备优化管理模型。并采用Benders分解算法将该模型有效地分解为一个与正常运行方式及相关约束有关的主问题和一系列与各预想故障及相应静态安全约束相关的子问题。提出了结合连续潮流方法的并行求解策略，有效地提高了该问题的求解效率。

本文在上述发电机无功储备的管理研究过程中还存在着几点不足：①未考虑与发电机直接连接的网络元件的故障，由于该类元件是否故障将直接影响发电机的无功注入，因此在发电机的无功储备管理过程当中需要考虑该类元件的影响；②本文所提方法适用于规模较小的系统，当系统规模较大时，考虑到无功电压问题的局部性，可以将电网进行分区，再利用本方法对各分区内的发电机无功储备进行优化管理。以上两点将是笔者后续工作中重点研究的内容。

参考文献：

［1］ Ruiz P A，Sauer P W.Reactive power reserve issues［C］// 38th Annual North American Power Symposium.Carbon⁃dale，USA，2006：439-445.

［2］程浩忠，吴浩.电力系统无功与电压稳定性［M］.北京：中国电力出版社，2004.

［3］张勇，罗滇生，范幸，等（Zhang Yong，Luo Diansheng，Fan Xing，et al）.STATCOM与传统电压无功控制手段协调应用（Coordination and application between STAT⁃COM and traditional voltage quality control means）［J］.电力系统及其自动化学报（Proceedings of the CSU-EP⁃SA），2015，27（12）：12-17，29.

［4］苏永春，程时杰，文劲宇（Su Yongchun，Cheng Shijie，Wen Jinyu）.用于提高电压稳定裕度的发电机无功出力管理（Reactive power generation management for im⁃provement of voltage stability margin）［J］.电力自动化设备（Electric Power Automation Equipment），2007，27（6）：39-42.

［5］熊虎岗，程浩忠，徐敬友（Xiong Hugang，Cheng Hao⁃zhong，Xu Jingyou）.考虑提高系统无功备用容量的无功优化调度（Optimal dispatch of reactive power consider⁃ing increase of system reactive power reserve）［J］.电网技术（Power System Technology），2006，30（23）：36-40.

［6］Arya L D，Singh P，Titare L S.Anticipatory reactive power reserve maximization using differential evolution［J］.Inter⁃national Journal of Electrical Power&Energy Systems，2012，35（1）：66-73.

［7］ Arya L D，Titare L S，Kothari D P.Improved particle swarm optimization applied to reactive power reserve max⁃imization［J］.International Journal of Electrical Power& Energy Systems，2010，32（5）：368-374.

［8］ Dong Feng，Chowdhury B H，Crow M L，et al.Improving voltage stability by reactive power reserve management［J］.IEEE Trans on Power Systems，2005，20（1）：338-345.

［9］ Alizadeh M O，Bozorg M，Cherkaoui R.Preventive reac⁃tive power management for improving voltage stability margin［J］.Electric Power Systems Research，2013，96：36-46.

［10］Mousavi O A，Bozorg M，Ahmadi-Khatir A，et al.Reactive power reserve management：preventive countermeasure for improving voltage stability margin［C］//IEEE Power and Energy Society General Meeting.San Diego，USA，2012.

［11］傅书逷（Fu Shuti）.IEEE PES 2004会议电网安全问题综述及防止大面积停电事故建议（Summary on power system security problems on 2004 IEEE PES meeting and recommendation for developing defense measures）［J］.电力系统自动化（Automation of Electric Power Systems），2005，29（8）：1-4.

［12］吴浩，郭瑞鹏，甘德强，等（Wu Hao，Guo Ruipeng，Gan Deqiang，et al）.发电机有效无功储备的分析和计算（Analysis and computation of effective reactive power re⁃serve of generators）［J］.电力系统自动化（Automation of Electric Power Systems），2011，35（15）：13-17，39.

［13］宫一玉，吴浩，宋卓然（Gong Yiyu，Wu Hao，Son Zhuor⁃an）.发电机无功储备的定义和评估（Definition and as⁃sessment of generator reactive power reserve）［J］.电网技术（Power System Technology），2013，37（7）：1902-1908.

［14］郭瑞鹏，吴浩，韩祯祥，等（Guo Ruipeng，Wu Hao，Han Zhenxiang，et al）.在线多预想故障静态电压崩溃预防控制（Online multi-contingency preventive control to avoid static voltage collapse）［J］.中国电机工程学报（Proceed⁃ings of the CSEE），2006，26（19）：1-6.

［15］王成山，张义（Wang Chengshan，Zhang Yi）.基于Bend⁃er's分解和内点法的无功优化规划（Optimal reactive power planning using Bender's decomposition technique and interior point method）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2003，15（4）：46-50，62.

［16］默哈莫德·夏班，刘皓明，李卫星，等（Mohamed Shaa⁃ban，Liu Haoming，Li Weixing，et al）.静态安全约束下基于Benders分解算法的可用传输容量计算（ATC calcu⁃lation with static security constraints using Benders de⁃composition）［J］.中国电机工程学报（Proceedings of the CSEE），2003，23（8）：7-11.

［17］刘明波，谢敏，赵维兴.大电网最优潮流计算［M］.北京：科学出版社，2010.

中图分类号：TM712

文献标志码：A

文章编号：1003-8930（2016）07-0083-06

DOI：10.3969/j.issn.1003-8930.2016.07.016

作者简介：

李 杰（1987—），男，硕士研究生，研究方向为电力系统稳定性分析与无功优化。Email：lijie82212@126.com

罗滇生（1971—），男，博士，教授，研究方向为电力市场理论研究及应用。Email：lhx20070322@hnu.edu.cn

李帅虎（1981—），男，博士，讲师，研究方向为电力系统稳定性分析与控制研究。Email：lishuaihu2010@126.com

收稿日期：2014-11-21；修回日期：2016-01-07

Application of Benders Algorithm to Reactive Power Reserve Management of Generators

LI Jie，LUO Diansheng，LI Shuaihu，WU Yingchang
（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

Abstract：The voltage stability of power system is closely related to the reactive power reserve of generators.First，a re⁃active power reserve management model is proposed with static security constraints under N-1 contingency fault condi⁃tions.Benders algorithm is applied to decompose the proposed model into a master problem relevant to normal condition and a series of subproblems relevant to N-1 contingency fault conditions：the master handles the constraints of normal condition and the Benders cut returned by the subs，and the subs handle the static security constraints corresponding to contingency fault.Second，to improve the solution efficiency of Benders algorithm，a parallel solution strategy com⁃bined with continuation power flow is given，thus the number of subproblems is reduced and only one Benders cut is re⁃turned to the master problem.A case study is conducted with IEEE 39-bus system，and the results show the correctness of the model and the effectiveness of the proposed strategy.

Key words：power system；static security constraint；reactive power reserve；Benders algorithm；contingency fault