基于多目标粒子群算法的配电网多目标优化重构

陈 萍，毛 弋，童 伟，邓海潮，陈艳平，胡躲华（湖南大学电气与信息工程学院，长沙 410082）

基于多目标粒子群算法的配电网多目标优化重构

陈 萍，毛 弋，童 伟，邓海潮，陈艳平，胡躲华
（湖南大学电气与信息工程学院，长沙 410082）

摘要：本文建立了系统有功损耗、节点最低电压幅值及开关操作次数的配电网多目标优化重构模型，并运用多目标粒子群优化算法求解。多目标粒子群算法的关键是如何选取个体的极值和全局极值，本文依据Pareto支配关系对个体极值进行选择，外部存储器就是全局极值的候选解集，计算外部存储器中各粒子与其他粒子的海明距离之和并作为各粒子的适应值，然后采用与适应值呈比例的轮盘赌方式选取粒子的全局最优位置，避免种群多样性的丧失。带时限的粒子全局极值淘汰策略使粒子能跳出局部最优，防止算法早熟收敛，保持了良好的收敛性。通过IEEE 33节点测试系统仿真计算，实验结果表明了该方法的可行性和有效性。

关键词：多目标优化；配电网重构；粒子群算法；Pareto支配；海明距离

配电网络中含有大量的常闭分段开关与少量的常开联络开关，配电网重构就是通过变换这些开关的开断状态来改变网络拓扑结构。通过重构可以降低网损、均衡线路负荷、消除过载、提高供电电压质量等［1］。以往的研究大多数只选取配电网的1个指标进行单目标优化［2-9］，而配电网重构是多目标非线性混合优化问题。传统的配电网多目标优化重构方法中，对多目标采取加权法［10-11］，将多目标问题转换成单目标后再加以求解。优化结果受权重系数影响较大，算法每次运行只能得到1个解，多次运行程序后才能得到1组近似Pareto最优解。文献［11-13］是单目标优化重构，单目标优化问题的目标函数只有1个，存在最优解；多目标优化问题有两个及以上的目标函数，求解得到1组折衷权衡多目标的Pareto解集。两者有着本质区别，所以基本粒子群算法无法直接用于求解多目标优化问题。

本文建立了系统有功损耗、节点最低电压幅值及开关操作次数的配电网重构多目标优化模型，采用基于粒子群算法与Pareto支配方法的结合来求解，即多目标粒子群算法。多目标粒子群算法的关键是选取个体的极值，建立1个外部存储器以存储迭代过程中的Pareto最优解，外部存储器中的解集就是全局极值的候选解，运用轮盘赌方式从外部存储器中选取；个体极值依据Pareto支配关系进行选择。粒子群算法实现简单、收敛速度快，但容易陷入局部最优从而导致早熟收敛。带时限的粒子全局极值淘汰策略使粒子能跳出局部最优，防止算法早熟收敛，较文献［4-12］结合禁忌搜索（Tabu）算法克服早熟，较文献［13］引入遗传算法的变异操作克服早熟的原理简单。典型IEEE 33节点测试系统实验结果表明算法保持了良好的收敛性，解集分布性、多样性较好。

1 多目标配电网重构的数学模型

1.1 目标函数

（1）有功损耗目标函数为

式中：L为系统支路总数；Ri、Ui、Pi、Qi分别为第i条支路的电阻、末端电压、有功功率、无功功率；Ki为支路上开关的状态，0表示断开，1表示闭合。

（2）开关操作次数目标函数［14］为

式中：Yi和Zj分别为分段开关和联络开关在重构后的状态，闭合时为1，断开时为0；m、n分别为配电网中的分段开关和联络开关数。

（3）节点最低电压幅值目标函数为

1.2 约束条件

（1）节点电压约束为Ui，min≤Ui≤Ui，max，Ui，min、Ui，max分别为节点i的上、下限电压。

（2）支路容量约束为Si≤Si，max，Si、Si，max分别是各支路流过的功率及支路的线路容量。

（3）网络拓扑约束为配电网络具有闭环设计、开环运行的特点，所以重构后的配电网络在运行时应呈福射状且无孤岛。

1.3 Pareto最优的概念

多目标优化问题的数学模型一般为

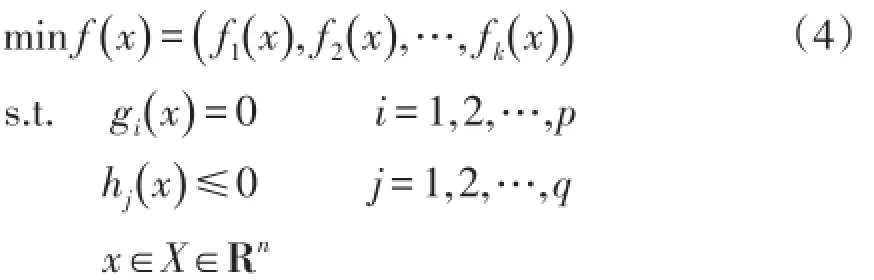
式中：fk（x）为第k个目标函数；gi（x）、hj（x）分别为等式约束和不等式约束。两个决策变量x1和x2，如果满足如下两个条件时，称解x1支配解x2：

（1）对于∀i=1，2，…，k，都满足fi（x1）≤fi（x2）；

（2）至少存在1个i∈｛1，2，…，k｝，使得fi（x1）＜fi（x2）。

满足上述条件的x1是多目标优化的一个Pareto最优解，亦称非劣解。所有Pareto最优解的集合构成Pareto最优解集。多目标优化问题的解不是唯一的，而是存在1组Pareto最优解集，解集间没有可比性。解的某个目标可能最优，而另一目标可能就弱于其他解。决策人员可根据实际问题的要求及操作的便捷性，从Pareto最优解集里面选出1个解或部分解作为所求多目标优化问题的最后方案。

2 多目标粒子群优化算法

2.1 二进制粒子群优化算法

二进制粒子群优化算法［15］将粒子每维位置限制为0和1，对应于开关的开/合状态，速度vid的大小决定位置xid取0或1的概率。粒子速度更新公式为

式中：vid为粒子i的第d维速度分量；xid为粒子i的第d维位置分量；w为惯性权重；c1、c2为学习因子；r1、r2为［0，1］之间的随机数；pid与gid分别为粒子i的历史最优位置和种群最优位置。配电网重构后呈辐射状且无孤岛，所以不在任何1个环路中的支路上的开关都必须闭合。粒子位置更新公式［16］为

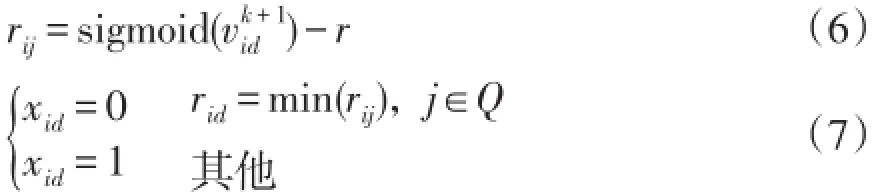
式中：r为［0，1］上的随机数；Q为与开关d属于同一个环路的所有开关的集合。式（6）和式（7）能够确保打开的开关数等于环路数，从而维持了配电网的辐射状结构。为了防止饱和，sigmoid函数设置为

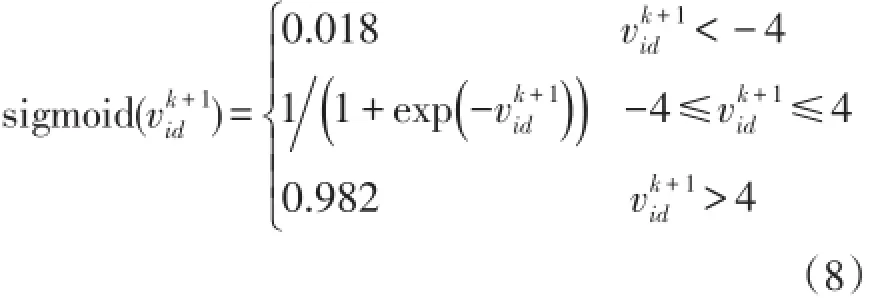
2.2 动态参数调节

惯性权重w表示先前速度对当前速度的影响程度，平衡全局搜索和局部搜索；学习因子调节个体最优位置的经验和全局最优位置的经验在速度更新中的比重。当w较大时，粒子进行全局寻优的能力强；当w较小时，粒子进行局部寻优的能力强。本文采取动态调整策略设置参数为

式中：wmin、wmax分别为惯性权重的最小值和最大值；c1、c2、cmin、cmax分别为学习因子的当前值、最小值、最大值；t为当前迭代次数；tmax为最大迭代次数。算法迭代初期w较大，有利于算法的全局搜索；迭代后期w逐渐减小，有利于算法的局部搜索。迭代初期，c1值较大，c2值较小，粒子对个体的认知能力强；迭代后期，c1值较小，c2值较大，粒子对全局极值的认知能力强。

2.3 外部存储器

种群在每次优化过程中粒子的位置都会发生变化，需要建立1个外部存储器，保存进化过程中产生的Pareto最优解，以引导算法更快地向非劣最优区域逼近。算法将每1代取得的非支配解集存放在存储单元B中，将到目前为止取得的最优解集存放在外部存储器A中。将非支配解集插入外部存储器的过程为：x∈B，如果任意A中的元素优于x，则舍弃x，如果x优于A中一系列解C，则A=A/C，A=A⋃｛x｝。运行至最大迭代次数时，外部存储器中的解个体即为所求的Pareto最优解集。若外部存储器的规模M超过了本身容量N，则采用基于拥挤距离［17］的剔除操作。根据拥挤距离的大小对外部存储器中的个体进行排序，剔除序列中最后1个个体，M=M-1。若M≤N，剔除操作完成，否则，重新计算个体的拥挤距离并排序，重复操作直至M≤N，剔除操作完成。

2.4 极值更新

对于个体极值，若粒子的新位置被粒子的个体极值支配，则用个体极值替代新位置；若粒子的新位置支配粒子的个体极值，则在新位置保持不变，若互不支配，则随机选择一个作为个体极值［18］。对于全局极值，外部存储器就是全局极值的候选集合，首先计算外部存储器中各个体与其他个体的海明距离之和，即二进制位串中不同位的个数，其公式为

式中E、D分别为外部存储器中个体数与粒子的维数。把海明距离的大小赋给对应个体作为其虚拟适应值（Fi=Hi），全局极值则是根据外部存储器中每个解的适应度值，采用与适应度值呈比例的轮盘赌方式从外部存储器中选择。

2.5 带时限的粒子全局极值淘汰策略

粒子i的全局极值在优化过程中若过于频繁地更换，势必会影响粒子群算法的寻优速度。同时，为了防止粒子群算法早熟收敛，提出1种带时限的粒子全局极值淘汰策略［19］以利于粒子在陷入局部最优时能跳出“陷阱”，利用粒子间的支配关系自动调整其时限值。种群粒子i选定了外部存储器中的某个非劣解作为全局极值时，该非劣解被赋予1个时限，初始值设为2。若时限值大于0，则当前全局极值能够引导群体向目标靠近，保留当前全局极值引导下一次迭代运行；若时限值减至0或者负数，则当前全局极值没有能力改善粒子，舍弃该全局极值，从外部存储器中重新选择1个非劣解作为粒子的全局极值。时限值调整过程为若粒子i的新位置被粒子i的历史最优位置支配，则当前全局极值的时限值减少1；若粒子i的新位置支配粒子i的历史最优位置，则当前全局极值的时限值增加1；若互不支配，则当前全局极值的时限值减少0.5。

3 算法流程

（1）输入配电网数据，生成满足辐射状要求的粒子种群规模，进行潮流计算并根据Pareto支配关系生成存储单元B（下文简记为B）并插入外部存储器A中（下文简记为A），剔除超出A规模的粒子。

（2）速度初始化为0，粒子的个体极值为粒子本身，计算A中Fi=Hi，并轮盘赌选择全局极值，赋予A中的全局极值的时限初值为2。

（3）调整w、c1、c2，更新粒子的速度与位置，判断是否达到最大迭代次数。若达到，则结束程序；若未达到，则转步骤（4）。

（4）进行潮流计算并根据Pareto支配关系生成B并插入A，剔除超出A规模的粒子。根据当前位置与粒子的历史最优位置的支配关系更新粒子的个体极值和当前全局极值的时限值。

（5）判断当前全局极值的时限值≤0是否满足。若不满足，则保持当前全局极值不变；若满足，则舍弃当前全局极值，计算A中Fi=Hi，并轮盘赌选择全局极值，转步骤（3）。

4 算例分析

本文采用IEEE 33节点配电系统算例［20］。如图1所示，其中有37条支路、33个节点、5个联络开关；额定电压为12.66 kV；有功功率为3 715 kW；无功功率为2 300 kvar。本文算法设种群规模为100；外部存储器规模为10；wmax=0.9，wmin=0.4；cmax= 2.5，cmin=0.5；tmax=100。本文算法得到的Pareto最优解集如表1和图2所示。配电网重构前打开的支路开关为33|34|35|36|37，系统初始网损为203.55 kW，节点最低电压为0.912 8 p.u.。以不同目标函数求解配电网单目标优化重构所得结果如表2所示。算法的收敛曲线如图3所示。

图1 IEEE 33节点系统Fig.1 IEEE 33 bus system

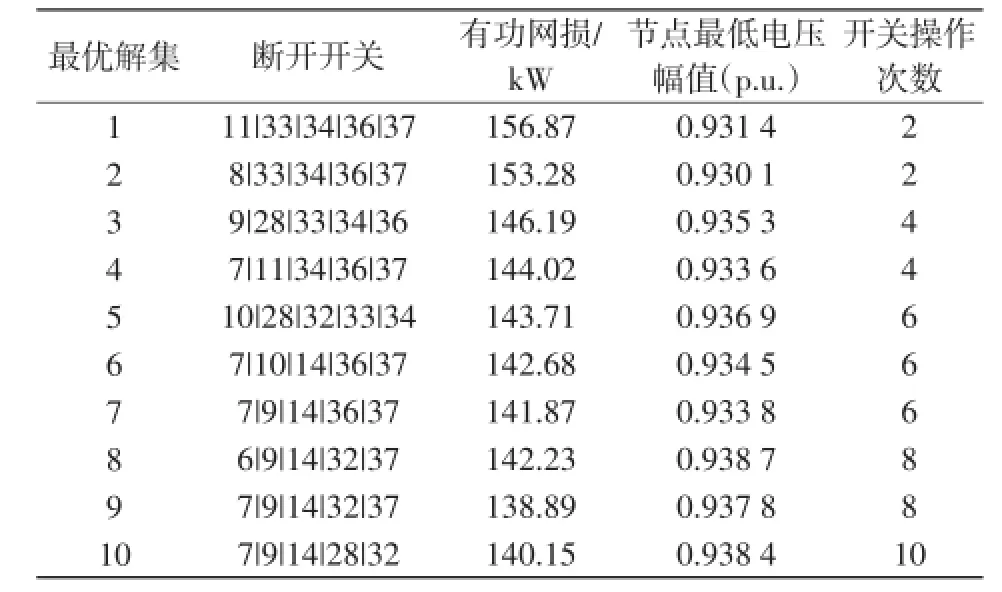
表1 算法的Pareto最优解集Tab.1 Pareto optimal solution set obtained by the proposed method

图2 Pareto最优解集分布Fig.2 Distribution of Pareto optimal solution set

从该仿真算例的结果来看，通过重构各种方案都降低了系统有功损耗，提高了系统节点电压水平。多目标粒子群优化算法的收敛性较好，为决策者提供了分布性、多样性较好的优化方案。运用本文的方法得到了一组重构结果，决策人员可以结合实际的情况，从中选出偏好的重构方案。这比以系统有功损耗、开关操作次数或者节点最低电压幅值为单目标得出的最优解有更好的合理性和实用性。

图3 算法的收敛曲线Fig.3 Convergence curve of the proposed method

5 结语

本文的配电网络重构方案兼顾多种重构目标，调度员可根据系统有功网损、节点最低电压幅值、开关操作次数选择合适的重构方案。采用基于支配的多目标粒子群算法进行求解，外部存储器基于拥挤距离的剔除操作保证了解集的分布性，全局极值的选取保持了种群的多样性，带时限的全局极值淘汰策略能防止算法陷入早熟，线性变化的惯性权重与学习因子提高了算法的性能，算法的收敛性较好。算例结果表明所用方法相对于单目标和加权多目标优化享有良好的优越性，算法一次运行可以得到多个Pareto最优解，为决策者提供了更多的决策方案，便于决策者根据实际系统的要求进行选择，实现了真正意义上的多目标优化，具有非常重要的实际意义。

参考文献：

［1］刘健，鹏翔，董海鹏.复杂配电网简化分析与优化［M］.北京：中国电力出版社，2002．

［2］姚李孝，任艳楠，费健安（Yao Lixiao，Ren Yannan，Fei Ji⁃an′an）.基于蚁群算法的配电网网络重构（Ant colony system algorithm for distribution network reconfiguration）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2007，19（6）：35-39．

［3］余健明，张凡（Yu Jianming，Zhang Fan）.基于改进免疫遗传算法的配电网重构（Distribution network reconfigu⁃ration based on improved immune genetic algorithm）［J］.电网技术（Power System Technology），2009，33（19）：100-105．

［4］许立雄，吕林，刘俊勇（Xu Lixiong，Lü Lin，Liu Junyong）.基于改进粒子群优化算法的配电网络重构（Modified particle swarm optimization for reconfiguration of distribu⁃tion network）［J］.电力系统自动化（Automation of Elec⁃tric Power Systems），2006，30（7）：27-30，79．

［5］刘莉，陈学允（Liu Li，Chen Xueyun）.基于模糊遗传算法的配电网络重构（Reconfiguration of distribution net⁃works based on fuzzy genetic algorithms）［J］.中国电机工程学报（Proceedings of the CSEE），2000，20（2）：66-69．

［6］靳小凌，赵建国（Jin Xiaoling，Zhao Jianguo）.基于改进二进制粒子群优化算法的负荷均衡化配电网重构（Distribution network reconfiguration for load balancing based on improved binary particle swarm optimization）［J］.电网技术（Power System Technology），2005，29（23）：40-43．

［7］邹必昌，龚庆武，李勋（Zou Bichang，Gong Qingwu，Li Xun）.基于负荷平衡的配电网重构遗传算法研究（Re⁃search on network reconfiguration GA in distribution sys⁃tem based on load balancing）［J］.电力系统保护与控制（Power System Protection and Control），2011，39（6）：80-83，111．

［8］HSU Y-Y，YI J-H，Liu S S，et al.Transformer and feeder load balancing using a heuristic search approach［J］.IEEE Trans on Power Systems，1993，8（1）：184-190．

［9］ 毕鹏翔，刘健，张文元（Bi Pengxiang，Liu Jian，Zhang Wenyuan）.以提高供电电压质量为目标的配网重构（Improve voltage quality by reconfiguration of distributed network）［J］.电网技术（Power System Technology），2002，26（2）：41-43，48．

［10］余健明，蔡利敏，杨文宇（Yu Jianming，Cai Limin，Yang Wenyu）.基于提高系统可靠性降低网损的配电网络重构（Distribution network reconfiguration for system reli⁃ability improvement and power loss reduction）［J］.电工技术学报（Transactions of China Electrotechnical Society），2004，19（10）：70-73．

［11］安源，彭先胜，姚李孝，等（An Yuan，Peng Xiansheng，Yao Lixiao，et al）.基于改进粒子群算法的配电网多目标重构（Multi-objective distribution network reconfigura⁃tion based on improved particle swarm algorithm）［J］.西安理工大学学报（Journal of Xi’an University of Technolo⁃gy），2010，26（2）：192-196．

［12］卢志刚，杨国良，张晓辉，等（Lu Zhigang，Yang Guo liang，Zhang Xiaohui，et al）.改进二进制粒子群优化算法在配电网络重构中的应用（Reconfiguration of distri⁃bution network based on improved particle swarm optimi⁃zation）［J］.电力系统保护与控制（Power System Protec⁃tion and Control），2009，37（7）：30-34．

［13］刘宏江，李林川，张长盛（Liu Hongjiang，Li Linchuan，Zhang Changsheng）.基于多种负荷方式的含分布式电源的配电网重构（Reconfiguration of distribution net⁃work with distributed generations based on various load modes）［J］.电力系统保护与控制（Power System Protec⁃tion and Control），2012，40（11）：117-121．

［14］景乾明，邹必昌，应若冰（Jing Qianming，Zou Bichang，Ying Ruobing）.含分布式发电以综合费用最低为目标的配电网重构（Reconfiguration of distribution network for the minimum comprehensive outlay with distributed generations）［J］.中国农村水利水电（China Rural Water and Hydropower），2011（9）：130-133．

［15］Kennedy J，Eberhart R C.A discrete binary version of the particle swarm algorithm［C］//IEEE International Confer⁃ence on Systems，Man，and Cybernetics.Orlando，USA，1997：4104-4108．

［16］黄涛，王倩，谭又宁（Huang Tao，Wang Qian，Tan Youning）.计及分布式电源的配电网重构研究（Research on the distribution network reconfiguration pondering dis⁃tributed generation）［J］.电力学报（Journal of Electric Power），2012，27（3）：199-202，206．

［17］Deb K，Pratap A，Agarwal S，et al.A fast and elitist multiobjective genetic algorithm：NSGA-II［J］.IEEE Trans on Evolutionary Computation，2002，6（2）：182-197．

［18］刘文颖，谢昶，文晶，等（Liu Wenying，Xie Chang，Wen Jing，et al）.基于小生境多目标粒子群算法的输电网检修计划优化（Optimization of transmission network main⁃tenance scheduling based on niche multi-objective parti⁃cle swarm algorithm）［J］.中国电机工程学报（Proceed⁃ings of the CSEE），2013，33（4）：141-148．

［19］谢承旺，李凯，徐君，等（Xie Chengwang，Li Kai，Xu Jun，et al）.一种改进型多目标粒子群优化算法MOPSO-II （An improved multi-objective particle swarm optimization algorithm MOPSO-II）［J］.武汉大学学报：理学版（Jour⁃nal of Wuhan University：Natural Science Edition），2014，60（2）：144-150．

［20］Goswami S K，Basu S K.A new algorithm for the reconfigu⁃ration of distribution feeders for loss minimization［J］.IEEE Trans on Power Delivery，1992，7（3）：1484-1491．

陈 萍（1987—），女，硕士研究生，研究方向为配电网规划、配电网重构。Email：410070487@qq.com

毛 弋（1965—），男，硕士，副教授，研究方向为配网自动化、电力系统规划。Email：maoyidu@yahoo.com.cn

童 伟（1987—），男，硕士研究生，研究方向为配电网规划、电能质量。Email：476035509@qq.com

中图分类号：TM72

文献标志码：A

文章编号：1003-8930（2016）07-0068-05

DOI：10.3969/j.issn.1003-8930.2016.07.013

作者简介：

收稿日期：2014-10-11；修回日期：2015-11-30

Multi-objective Distribution Network Reconfiguration Based on Multi-objective Particle Swarm Optimization

CHEN Ping，MAO Yi，TONG Wei，DENG Haichao，CHEN Yanping，HU Duohua
（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

Abstract：A multi-objective optimal reconfiguration model for distribution network system with minimization of power loss，minimum voltage value of the node and numbers of switches changing is built，and the multi-objective particle swarm optimization（MOPSO）is applied to solve the model.The key of the MOPSO is how to select the personal best and the global best.According to Pareto dominance criterion，the personal best is selected.Taking the Hamming dis⁃tance of each particle of the external archive as its fitness value，then the global best is selected by roulettle proportional to the fitness，maintaining the diversity of the population.With a time limit global best phase-out strategy makes parti⁃cles jump out local optima，avoiding the algorithm into premature convergence and maintaining a good convergence.Simulated calculation results by using the IEEE 33 bus test system demonstrate the feasibility and effectiveness of the proposed method.

Key words：multi-objective optimization；distribution network reconfiguration；particle swarm algorithm；Pareto domi⁃nance；Hamming distance