道砟材料累积沉降量和形变模量的离散元分析
严颖,赵金凤,季顺迎
(1.大连交通大学 土木与安全工程学院,辽宁 大连 116028;2.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116023)
道砟材料累积沉降量和形变模量的离散元分析
严颖1,赵金凤2,季顺迎2
(1.大连交通大学 土木与安全工程学院,辽宁 大连 116028;2.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116023)
摘要:针对铁路有砟道床中碎石材料在细观上的非规则形态,采用离散元模型构造道砟颗粒,并通过道砟箱试验数值分析道砟材料在往复荷载下的累积沉降量和形变模量。计算结果表明:在往复荷载作用下道砟材料的累积沉降量与加载次数呈指数关系,其形变模量随加载次数的增加不断增加并逐渐趋于稳定。在此基础上,对道砟摩擦因数和加载频率影响下的累积沉降量和形变模量进行离散元分析。随摩擦因数的增大,道砟颗粒间的咬合力不断增加,致使道砟材料的累积沉降量减小而有效刚度越大;随加载频率的增大,道砟材料更趋于密实排列,从而使其累积沉降量增大而形变模量降低。本文研究表明离散元模型在分析道砟材料力学特性方面具有较高的可行性,并有助于进一步揭示有砟铁路道床的累积变形规律。
关键词:道砟材料;离散元模型;累积沉降量;形变模量;摩擦因数
有砟道床的主要功能是承受并传递来自轨枕的荷载,保持轨道几何状态的稳定性,并减缓和吸收轮轨的冲击和振动。在列车荷载的重复作用下,有砟道床的弹性和变形受道砟颗粒重新排列、破碎粉化的影响有很大的变化,其塑性变形是轨道结构残余变形的主要原因[1]。对有砟道床累积沉降特性和有效弹性的研究有助于揭示轨道结构的劣化机理[2-4]。有砟道床的累积沉降量和形变模量一般随往复荷载作用次数的增加而增大,并当荷载作用次数达到一定程度时趋于稳定[1-2,5]。通过动三轴试验还研究了荷载、道床密实度和道砟材料等因素对道床永久变形的影响[1]。为模拟道砟的真实工作状态,采用道砟箱试验研究道砟在准静态和往复荷载下的沉降过程。结果表明,道砟颗粒的形态和破碎对道砟材料的沉降变形影响显著[6-8]。然而,对有砟道床的沉降特性及有效模量与外部荷载特性、初始铺设条件、道砟级配和材质等影响因素的对应关系还尚未进行全面深入地研究。为研究有砟道床的动力特性,人们开展了一系列的数值分析。考虑道砟的刚度等物理参数对道床沉降量的影响,用有限元方法模拟了道床在往复荷载作用下的累计变形特性[9-11]。然而,基于连续介质力学的有限元方法未考虑细观尺度下道砟颗粒在往复荷载下的重新排列和破碎特性,不能分析道砟形态、粒径等因素的影响。针对道砟材料的非连续分布特征,离散单元法能够精确地模拟道砟颗粒的粒径、形状、级配、孔隙率等细观特征,以及道砟的破碎粉化过程等,计算结果更加接近工程实际[12-13]。近年来,针对有砟道床的离散结构特性,离散元方法已成功地用于道床累积沉降量和变形模量中的研究,以及道床的捣固过程分析[14-18]。在道砟动力特性的离散元分析中,最初采用规则的圆盘或球体单元模拟道砟颗粒[14-15]。为更合理地描述道砟颗粒的非规则几何形态,人们采用球形颗粒的不同黏接和镶嵌组合形式,以更准确地分析其宏观力学行为[19-22]。采用球体单元的黏结模型可模拟道砟材料在往复列列车荷载下破碎粉化特性[23-25]。为更加精确地表征道砟颗粒的非规则形态,可采用更小粒径的球体颗粒,但单元数目的增加会急剧降低离散元的计算效率[26-27]。此外,采用多面体单元也是有效模拟道砟材料的途径[19,27]。在细观尺度下合理地构造道砟颗粒形态不仅有助于提高计算效率,更重要的是可以更准确地确定道砟材料的宏观力学行为。本文采用球体单元的不同镶嵌组合模式构造非规则形态的道砟颗粒,在往复荷载下对道砟箱试验进行离散元分析,探讨道砟材料的累积沉降规律和形变模量特性。

1道砟箱试验的离散单元模型
1.1非规则形态道砟颗粒的构造
道砟碎石一般为具有一定棱角的非规则多面体结构,如图1所示。针对道砟颗粒的几何形态,本文采用球形颗粒的镶嵌组合方法进行构造。首先依据道砟碎石的粒径和几何形态构造相应的多面体结构,然后在该多面体结构内填充球形颗粒,并让球体膨胀到设计尺寸,从而形成具有非规则形态的道砟单元。这里选取6个不同形态的道砟单元如图2所示。道砟单元由若干个球形颗粒按不同重叠量和几何方位镶嵌而成,其体积、质心和转动惯量可采用有限分割法进行确定[28]。由于道砟碎石粒径在工程应用中有很宽的分布范围,一般在16~63 mm范围内,其中31.5~50 mm级配内的道砟在50%以上[29]。为提高离散元方法的计算效率,又能反映出道砟材料的力学性能,可选用较大粒径颗粒进行离散元分析[20,24]。为此,本文构造的道砟颗粒尺寸在37~54 mm之间。

图1 具有非规则形态的道砟颗粒Fig.1 Ballast particles with irregular shape

图2 铁路道砟的离散单元模型Fig.2 Discrete element model of railway ballasts
对各道砟颗粒分别建立整体坐标和局部坐标,在局部坐标下计算各球体单元的作用力,以及道砟单元的受力和角速度,在整体坐标下计算道砟颗粒的速度和位移;采用四元数方法对2个坐标系间的参量进行转换计算[28]。此外,本文采用Hertz-Mindlin非线性接触模型计算颗粒单元间的作用力。在法线方向上,颗粒之间的作用力包括Hertz弹性力和非线性黏滞力。在颗粒接触的切线方向,采用Mindlin理论和Mohr-Coulomb摩擦定律进行计算。对于非线性接触模型,时间步长由颗粒密度、泊松比和剪切模量确定[31]。
1.2道砟箱模型的离散元构造
本文通过道砟箱试验分析道砟材料在往复荷载下的动力过程。参考相关道砟箱试验结构,这里选取道砟箱尺寸为700 mm×300 mm×450 mm,由此道砟碎石可在7层以上。在对往复加载的道砟箱试验的离散元模拟中,采用的主要计算参数见表1。
表1道砟箱试验离散单元模拟中的主要计算参数
Table 1 Main computational parameters in DEM simulations of ballast box test

参数数值道砟箱尺寸/mm3700×300×450枕木尺寸/mm3295×250×170道砟粒径/mm37~54道砟刚度/(N·m-1)7.25×107道砟密度/(kg·m-3)2545.0颗粒间摩擦因数0.1~1.0颗粒与侧壁摩擦因数0.2最大加载力/kN30.5最小加载力/kN5.5
在离散元数值模拟中,将道砟颗粒随机放置于道砟箱内。初始道砟颗粒设为其实际粒径的0.4倍,然后缓慢生长到所需粒径。在颗粒生长过程中,颗粒之间因相互碰撞而达到新的平衡位置。道砟材料初始排列完成后,将轨枕缓慢放至道砟材料表面,如图3所示。对轨枕缓慢加载至Fmean,然后施加正弦往复荷载,其最大值和最小值分别为Fmax和Fmin。在道砟箱试验的离散元模拟中,轨枕的长度为295 mm,其要明确小于标准钢轨宽度。同时考虑列车对轨枕的冲击特性,这里取最小荷载Fmin=5.5 kN,平均荷载Fmean=18.0 kN和最大荷载Fmax=30.5 kN,加载频率f0=5 Hz。在Lu等的道砟箱试验离散元计算中取最大荷载40 kN,加载频率为3 Hz[7],高亮等的离散元模拟中在整个轨枕上施加的最大荷载为70 kN,加载频率为10 Hz[30]。

图3 道砟箱试验的离散单元模型Fig.3 Discrete element model of ballast box test
2道砟材料累积沉降量和形变模量的离散元分析
2.1往复荷载下道砟材料的累积沉降量和形变模量
采用镶嵌组合颗粒单元,对道砟箱在往复荷载下的动力过程进行了离散元计算,其在35个荷载周期下的计算结果如图4所示。图4(a)为荷载情况,图4(b)为荷载与枕木沉降量间的关系。在第一个加载周期,道床的沉降量较大;随着加载次数的增加,沉降曲线越来越密实,即轨枕沉降趋于平稳。
图4(c)为轨枕累积沉降量随加载次数的演变情况。可以发现,轨枕沉降量随往复荷载呈周期性变化,累计下沉量随往复荷载次数的增加不断增大,但是增长趋势逐渐趋于平缓。这主要是由于道砟颗粒在加载初期排列相对疏松,而在往复荷载的作用下不断重新密实排列,并随加载次数的增加其内部排列不断密实,进而使其累积沉降量趋于平稳。从图4(c)呈现的计算结果来看,道砟材料在35个周期荷载作用下的累积沉降量可达4.5 mm。这与Mcdowell等的离散元模拟结果接近[6,14]。
为进一步分析道砟材料在往复荷载下的弹性演化趋势,这里对轨枕所受作用力P与其对应位移u进行线性拟合,并定义其形变模量为:
(1)
形变模量M单位为N/m。

(a)正弦往复荷载;(b)荷载P与累积沉降量u的对应关系;(c)累积沉降量u随加载次数N的变化趋势图4 离散元模拟的道床在往复荷载作用下的P-u曲线Fig.4 P-u curves of ballast track under cyclic loading simulated with DEM
这里以第2次加载周期为例(如图5(a)所示),荷载P与轨枕沉降量u呈现良好的线性关系,即:
P=13.34u-10.62
(2)
式中,荷载P单位为kN,沉降量u单位为mm。这里的斜率即为道砟材料的形变模量,即M=13.34×106N/m。该形变模量的拟合残差R2=0.999 6,表明荷载与沉降量具有很好的线性关系。由此对35个加载周期的形变模量进行确定,结果如图5(b)所示。在最初几个加载周期内,形变模量增长明显,但随着加载周期的增加,形变模量趋于平缓。从图4(c)和图5(b)可以看出,道砟材料的累积沉降量一直随加载次数的增加而增加,而其形变模量则很快趋于稳定。道砟材料形变模量和累积沉降量均有效地反映了有砟道床在往复荷载作用下的密实过程,分别表征了道床有效弹性和永久变形的演化规律。

(a)P-u线性拟合;(b)形变模量随加载次数的变化趋势图5 道砟材料P-u对应关系及形变模量演化规律Fig.5 P-u relationship of ballast materials and deformation modulus
2.2往复荷载下道砟材料内部的力链分布
力链是散体材料内部各颗粒间作用力的主要传递方式。从细观尺度上分析往复荷载作用下道砟颗粒间力链的空间结构和强度分布,有助于揭示道砟材料的基本力学行为。
取一个加载周期内道砟颗粒间的力链分布如图6所示。当t=1.65 s时,对轨枕施加最小作用力P=5.5 kN,此时力链分布均匀且强度较弱,最大接触力为285.32 N,颗粒之间接触充分,接触数为4 919。当t=1.81 s时,轨枕施加于道砟上的作用力增加到30.5 kN。此时颗粒间的最大接触力增加到898.23 N。在该过程中道砟颗粒间的力链明显发生断裂和重构过程,强力链主要分布于枕木下方,呈辐射状分布。
当t=1.98 s时,即在卸载至P=5.5 kN时,颗粒之间的接触再次发生变化,力链重新组构,强力链发生断裂。此时,颗粒之间的最大接触力为365.72 N,接触数为3 272。由此可见,在加载-卸载过程中,由于道砟颗粒间的相互移动、错动、重新排列组合,从而使颗粒间的力链结构发生相应的变化。

(a)t=1.65 s;(b)t=1.73 s;(c)t=1.81 s;(d)t=1.98 s图6 循环荷载下力链分布Fig.6 Force chain distribution under cyclic loading
3道砟材料累积沉降及形变模量的影响因素分析
3.1道砟颗粒间摩擦因数的影响
摩擦因数是道砟表面粗糙程度的一个表征,摩擦因数越大,道砟颗粒越粗糙。有砟道床的累积沉降量和形变模量与碎石的摩擦因数密切相关。这里取道砟颗粒间的摩擦因数μ= 0.4,0.45,0.5,0.55和0.6时,对道砟箱试验在10次往复加载下进行离散元分析。不同摩擦因数下得到的轨枕位移变化如图7(a)所示,可发现道砟材料的累积沉降量随加载次数而不断增加。这与图4(c)所示结果相一致。由图7(a)确定的不同摩擦因数下第10个加载周期时的累积沉降量如图7(b)所示。可以发现,随着摩擦因数的增加,轨枕沉降量不断减小,且当μ<0.5时,沉降量受摩擦因数的影响更加明显。这是由于摩擦因数较小时,道砟颗粒间的摩擦阻力减小,致使轨枕更容易发生沉降;当摩擦因数较大时,道砟颗粒间的滑动摩擦增加,致使其滚动方式显著增加,并成为道砟相对运动的主要形式。
为进一步分析摩擦因数对道砟材料形变模量的影响,对以上不同摩擦因数第10次加载时作用力P与位移u进行线性拟合,结果如图8所示。可以发现,形变模量随摩擦因数的增加而增大。这主要是由于道砟颗粒间摩擦因数的增大,会使颗粒间的摩擦阻力增加,从而限制颗粒的相互运动。

(a)轨枕沉降量变化;(b)第10个加载周期的道砟材料累积沉降量图7 不同摩擦系数下离散元模拟的轨枕沉降量Fig.7 Accumulated settlement of sleeper simulated with DEM
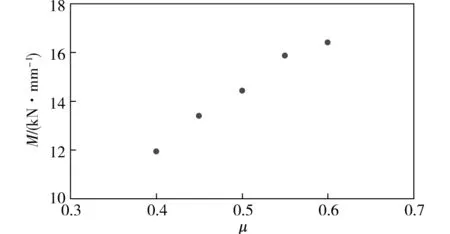
图8 道砟材料有效刚度与摩擦因数的对应关系Fig.8 Relationship between the effective stiffness and the inter-particle friction coefficient of ballast materials
3.2加载频率的影响
道床沉降量与形变模量变化与列车的行驶速度,即往复荷载的频率密切相关。本文对道砟箱试验在加载频率分别为3,5,10,15和20 Hz时进行了10个周期的离散元分析,计算得到的轨枕沉降过程如图9(a)所示,由此得到第10个加载周期时的累积沉降量如图9(b)所示。可以发现,在高频荷载作用下,道砟材料在相同加载次数下的累积沉降量明显增大。这是由于高频加载下道床的弹性变形恢复时间短,同时高频的振动使道砟材料运动加速,从而更容易重新排列。由此可见,在列车高速运行中,有砟道床更容易发生沉降变形。
不同加载频率下第10次加载时作用力P与位移u进行线性拟合,得到的形变模量如图10所示。可以发现,加载频率对道床的形变模量影响比较明显。加载频率越高,道床的形变模量越小。这是由于道砟颗粒在高频荷载作用下振动较强,从而更容易发生疏松排列,致使其形变模量迅速降低。

(a)轨枕沉降量变化;(b)第10个加载周期的道砟材料累积沉降量图9 不同加载频率下轨枕的沉降值Fig.9 Settlement of sleeper under different loading frequencies

图10 不同加载频率下道砟材料的形变模量Fig.10 Deformation modulus of ballast materials under different loading frequencies
4结语
1)针对铁路道砟碎石的细观几何结构特点,采用球体组合镶嵌方式构造道砟颗粒,对道砟材料在往复荷载下的累积沉降和弹性特征进行了离散元数值分析,验证了离散元方法在研究有砟道床动力学中的可行性。
2)道砟材料的累积沉降量和形变模量均随加载次数而增大并趋于稳定,在加载过程中道砟颗粒间的强力链主要分布在轨枕下方,并呈辐射状分布。
3)道砟材料的累积沉降量随道砟颗粒间摩擦因数的增大而减小,随加载频率的增加而增大;形变模量则随摩擦因数的增加而增大,随加载频率的增加而减小。
参考文献:
[1] 王红. 道碴弹性与累积变形的试验研究[J]. 中国铁道科学, 2001,22(6):106-110.
WANG Hong. Test and study on ballast elasticity and accumulated deformation[J]. China Railway Science, 2001, 22(6):106-110.
[2] 胡仁伟,赵钢,王红,等. 道床累积变形模型的改进及荷载作用顺序对累积变形的影响[J].铁道学报, 2001,23(6):81-84.
HU Renwei, ZHAO Gang, WANG Hong, et al. An advanced model of ballast accumulated deformation and the effect of load order on accumulated deformation[J]. Journal of the China Railway Society, 2001, 23(6):81-84.
[3] 高建敏, 翟婉明, 徐涌. 有碴轨道下沉变形参数影响分析[J]. 交通运输工程学报, 2007, 7(4): 15-20.
GAO Jianmin, ZHAI Wanming, XU Yong. Analysis of parameters’ effects on settlement of ballasted track[J] Journal of Traffic and Transportation Engineering, 2007, 7(4): 15- 20.
[4] 井国庆, 封坤, 高亮, 等. 循环荷载作用下道砟破碎老化的离散元仿真[J]. 西南交通大学学报, 2012, 47(2): 187-191.
JING Gouqing, FENG Kun, GAO Liang, et al. DEM simulation of ballast degradation and breakage under cyclic loading[J]. Journal of Southwest Jiaotong University, 2012, 47(2): 187-191.
[5] Suiker A S J, Selig E T, Frenkel R. Static and cyclic triaxial testing of ballast and subballast[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(6): 771-782.
[6] Mcdowell G R, Lim W L, Collop A C, et al. Laboratory simulation of the effects of train loading and tamping on ballast performance[J]. Proceedings of the Institution of Civil Engineers, 2005, May: 89-95.
[7] Lu M, Mcdowell G R. Discrete element modelling of ballast abrasion[J]. Geotechnique, 2006, 56(9): 651-655.
[8] Huang H, Chrismer S. Discrete element modeling of ballast settlement under trains moving at “Critical Speeds” [J]. Construction and Building Materials, 2013, 38: 994-1000.
[9] Zhai W M, Wang K Y, Lin J H. Modeling and experiment of railway ballast vibrations[J]. Journal of Sound and Vibration, 2004, 270(4-5): 673-683.
[10] 朱剑月, 练松良. 基于轨道元的运动有限元分析[J]. 铁道学报, 2009, 31(3):65-68.
ZHU Jianyue, LIAN Songliang. A moving finite element algorithm for the adaptive solution of dynamic behavior of railway track structures [J]. Journal of the China Railway Society, 2009, 31(3):65-68.
[11] Suiker S J, De Borst R. A numerical model for the cyclic deterioration of railway tracks[J]. International Journal for Numerical Methods in Engineering, 2003, 57: 441-470.
[12] Lu M, Mcdowell G R. Discrete element modelling of railway ballast under monotonic and cyclic triaxial loading[J]. Geotechnique, 2010, 60(6): 459-467.
[13] 肖宏, 高亮, 侯博文. 铁路道床振动特性的三维离散元分析[J]. 铁道工程学报, 2009(9): 14-17.
XIAO Hong, GAO Liang, HOU Bowen. Analysis of ballast dynamic behavior with three-dimensional discrete element method[J]. Journal of Railway Engineering Society, 2009(9): 14-17.
[14] Lobo-Guerrero S, Vallejo L E. Discrete element method analysis of railtrack ballast degradation during cyclic loading[J]. Granular Matter, 2006, 8:195-204.
[15] Zeghal. Discrete-element method investigation of the resilient behavior of granular materials[J]. Journal of Transportation Engineering, 2004, 130(4): 503-509.
[16] Makoto I, Takahiro S. Effect on track settlement of interaction excited by leading and trailing axles[J]. Quarterly Report of RTRI, 2005, 46(1): 1-6.
[17] Saussine G, Cholet C, Gautier P E, et al. Modelling ballast behaviour underdynamic loading. Part I: A 2D polygonal discrete element method approach[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195:2841-2859.
[18] Tutumluer E, Huang H, Hashash Y M A, et al. Aggregate shape effects on ballast tamping and railroad track lateral stability[C]// American Railway Engineering and Maintenance of Way Association (AREMA) Annual Conference, Louisville, KY, September, 2006: 17-20.
[19] 严颖, 狄少丞, 苏勇, 等. 风沙影响下铁路道碴变形模量的离散元数值分析[J]. 计算力学学报, 2012, 29(3): 339-445.
YAN Ying, DI Shaocheng, SU Yong, et al. Discrete element analysis of elastic modulus of railway ballasts in wind with different sand contents[J]. Chinese Journal of Computational Mechanics, 2012, 29(3): 339-445.
[20] Lu M, Mcdowell G R. The importance of modeling ballast particle shape in the discrete element method[J]. Granular Matter, 2007, 9(1-2): 69-80.
[21] Chen C, Mcdowell G R, Thom N H. Discrete element modelling of cyclic loads of geogrid-reinforced ballast under confined and unconfined conditions[J]. Geotextiles and Geomembranes, 2012, 35:76-86.
[22] Ferellec J, Mcdowell G R. A method to model realistic particle shape and inertia in DEM[J]. Granular Matter, 2010, 12:459-467.
[23] Hossain Z, Indraratna B, Darve F, et al. DEM analysis of angular ballast breakage under cyclic loading[J].Geomechanics and Geoengineering: An International Journal, 2007, 2(3): 175-181.
[24] Lim W L, Mcdowell G R. Discrete element modeling of railway ballast[J]. Granular Matter, 2005, 7: 19-29 .
[25] Ergenzinger C, Seifried R, Eberhard P. A discrete element model predicting the strength of ballast stones[J]. Computers and Structures, 2012, 108/109: 3-13.
[26] Gao R, Du X, Zeng Y, et al. A new method to simulate irregular particles by discrete element method[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2012, 4 (3): 276-281.
[27] Zhao D, Nezami E G, Hashash Y M A, et al. Three-dimensional discrete element simulation for granular materials[J]. Engineering Computations, 2006, 23(7):749-770.
[28] Yan Y, Ji S. Discrete element modeling of direct shear tests for a granular material[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 34: 978-990.
[29] TB/T 2140—2008,铁路碎石道砟[S].
TB/T 2140—2008, Railway ballast[S].
[30] 高亮, 罗奇, 徐旸, 等. 基于离散元法的铁路道床力学特性[J]. 同济大学学报(自然科学版), 2014, 42(7): 1064-1068.
GAO Liang, LUO Qi, XU Yang, et al. Railway ballast bed mechanical property based on discrete element method[J]. Journal of Tongji University (Natural Science), 2014, 42(7): 1064-1068.
[31] Kremmer M, Favier J F. A method for representing boundaries in discrete element modelling-Part II: Kinematics[J]. International Journal for Numerical Methods in Engineering, 2001, 51:1423-1436.
* 收稿日期:2015-09-20
基金项目:国家自然科学基金资助项目(11172063,11572067,U1234209)
通讯作者:季顺迎(1972-),男,河北武邑人,教授,博士,从事颗粒材料计算力学及工程应用研究; E-mail: jisy@dlut.edu.cn
中图分类号:U213.7+2; O158
文献标志码:A
文章编号:1672-7029(2016)06-1031-08
Discrete element analysis of settlement and deformation modulus of railway ballasts
YAN Ying1,ZHAO Jingfeng2,JI Shunying2
(1.School of Civil and Safety Engineering, Dalian Jiaotong University, Dalian 116028, China;2.State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116023, China)
Abstract:This study investigates settlement and deformation modulus of railway ballasts under repeated loads through ballast box tests by using discrete element method and considering the irregular shapes of ballasts. Simulated results present an exponential relationship between settlement and loading cycles. Deformation modulus of ballasts increases with increasing loading cycles and tends to be constant. Based on the developed discrete element model, this study also explores the influential factors, such as friction coefficients of ballasts and loading frequency. The results show that settlement reduces and deformation modulus increases with increasing friction coefficients because of the increasing interlocking between particles. Settlement increases and deformation modulus reduces with increasing loading rates because of the corresponding compact packing. This study shows the feasibility and contribution of the discrete element method in the understanding of the mechanical characteristics of railway ballasts.
Key words:ballasts; discrete element method; settlement; deformation modulus; friction coefficient

