基于维度特性的二维到达角及极化参量联合估计算法*
吴 娜,司伟建,焦淑红
(哈尔滨工程大学信息与通信工程学院,哈尔滨 150001)
基于维度特性的二维到达角及极化参量联合估计算法*
吴娜,司伟建,焦淑红
(哈尔滨工程大学信息与通信工程学院,哈尔滨150001)
摘要:针对利用极化敏感阵列进行多维参数联合估计运算复杂度大的问题,提出一种基于噪声子空间维度特性的极化敏感阵列DOA及极化参数联合估计算法。算法利用阵列接收数据协方差矩阵噪声子空间的维度特性构造谱函数,有效降低了极化敏感阵列信号参数联合估计的计算复杂度,同时保证了算法的估计性能。对算法与现有基于长矢量的MUSIC算法的运算复杂度进行了理论分析对比。最后,仿真对比实验验证了算法的有效性。
关键词:极化敏感阵列;维度特性;DOA估计;极化参量估计
0引言
近几十年来,基于极化敏感阵列的空间信号到达角(directionofarrival,DOA)和极化参数的联合估计问题受到相关学者的广泛关注[1-6]。利用极化敏感阵列可以实现信号DOA和极化参数的联合估计,获得更多入射信号的信息,从而提高阵列的接收能力,改善相应的DOA估计性能。
极化敏感阵列将空间域的参数估计扩展为空间极化域联合参数估计问题,相比于空间域的二维搜索,空间极化域的四维搜索需要的计算量相当高,严重制约了该类算法在实际工程中的应用。MUSIC算法的巨大计算量主要集中于两部分,即特征值分解和空间谱的构造,其中构造空间谱需要的运算量要远远大于特征值分解运算的运算量。因此,如果可以降低空间谱构造的运算量就可以大大减少MUSIC算法的总运算量。文献[7-11]将MUSIC算法扩展应用到了极化敏感阵列;文献[12]研究了用于极化敏感阵列的基于长矢量MUSIC算法(longvector-basedMUSIC,LV-MUSIC),该方法基于长矢量数学模型,具有较高的估计精度,但运算量巨大;文献[13]研究了基于四元数理论的信号入射角和极化参量的联合估计问题,利用四元数在运算量上的优势,降低了算法的运算次数,但由于四元数由1个实部和3个虚部构成,每次运算需要的运算时间变长,因此总体运算时间并没有降低,同时由于减少了矩阵维数,因此在分辨力上相比于LV-MUSIC算法有所下降。
文中提出一种适用于极化敏感阵列二维到达角和极化参数联合估计算法(dimensionfeature-basedMUSIC,DF-MUSIC)。针对MUSIC算法谱峰搜索运算量大的问题,降低每个谱峰值求解的运算量,从而降低基于长矢量的MUSIC类算法的运算量,并且保留了长矢量数据模型在估计精度上的优势。为了简便,文中算法的理论推导及计算机仿真均假设信号的极化相位差是已知的。但是在极化相位差未知的情况下,所提算法仍然适用。最后,通过计算机仿真对比实验验证了算法的有效性。
1数学模型
由N=M×M对正交偶极子构成的均匀平面阵列如图1所示。其中第il(i,l=1,2,…,M)个偶极子对的中心坐标为(x,y)=((i-1)d,(l-1)d),相邻偶极子对之间的间隔为d,数值等于入射信号源的半波长。
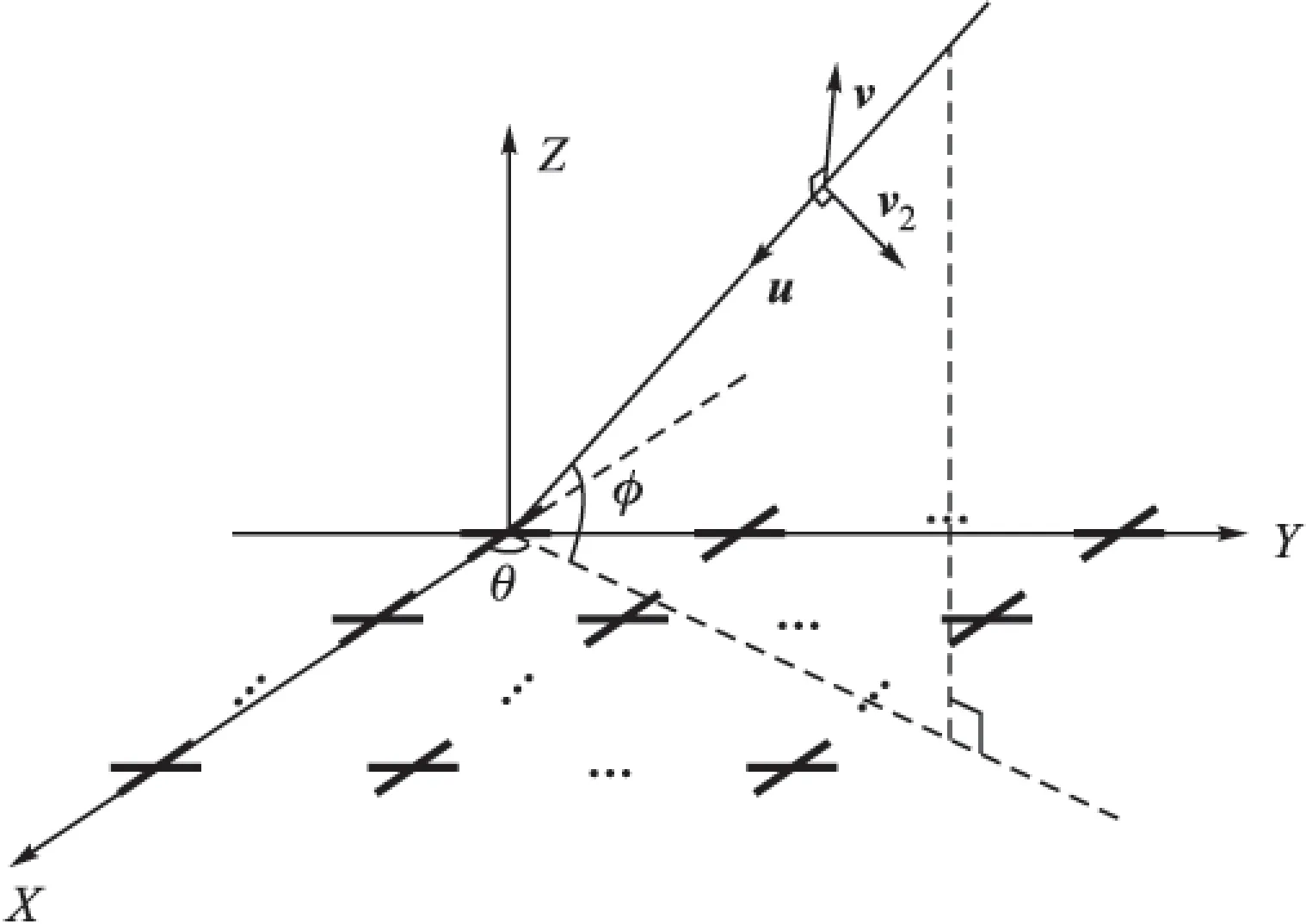
图1 极化敏感均匀平面阵
设有K个远场静态随机信号入射到天线阵列。定义第k个入射信号的DOA和极化参数分别为(θk,φk)和(γk,ηk),为了简便且不失一般性,设ηk=90°,即入射信号的极化在坡印廷球面的同一圆周上[1]。
极化敏感阵列的接收数据的矩阵形式为:

(1)
式中:X(t)=[x1(t)x2(t)…x2N(t)]T∈C2N×1为接收信号矢量;S(t)=[s1(t)s2(t)…sK(t)]T∈CK×1为信号源矢量;N(t)是2N×1维协方差矩阵为σ2I2N的零均值高斯白噪声矢量。A(θ,φ,γ)∈C2N×K为流型矩阵,具体形式如下:
A(θ,φ,γ)=
(2)
式中:a(θk,φk,γk)=as(θk,φk)⊗ap(θk,φk,γk),(k=1,2,…,K),“⊗”为克罗内克积,as(θk,φk)称为阵列流型矢量,具体形式如下:
as(θk,φk)=
(3)
ap(θk,φk,γk)称为极化矢量,其表达式为:
(4)
将极化敏感阵列接收数据矢量的奇数位数据取出得到沿X轴方向的N个偶极子的接收数据矢量,定义为子阵Xx(t),矢量形式为:
(5)
同理,取出对应偶数位的信息得到沿Y轴方向的N个偶极子的接收数据矢量,定义为子阵Xy(t),矢量形式为:
(6)
将阵列接收数据矢量重新排列,得到新的阵列接收数据矢量为:
(7)
设阵列接收的噪声为零均值加性空间平稳高斯白噪声,噪声功率为σ2,则对应的新数据协方差矩阵为:
(8)
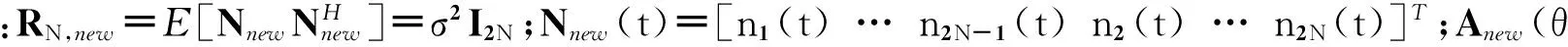
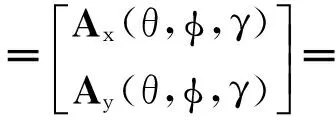
(9)
在实际中,天线接收的数据为有限长的,因此常用最大似然估计方法得到数据协方差矩阵的估计值,即:
(10)
2DF-MUSIC算法基本原理
2.1算法基本原理
对数据协方差矩阵Rx进行特征分解得:
(11)
(12)
其中第一组包含前K个大特征值,其对应的特征矢量构成信号子空间US=[u1u2…uK],第二组包含从第K+1到第N个小特征值,其对应的特征矢量构成矩阵UN1=[uK+1uK+2…uN],该矩阵张成的空间包含于噪声子空间,第三组包含后N个小特征值,其对应的特征矢量构成矩阵UN2=[uN+1uN+2…u2N],该矩阵张成的空间同样包含于噪声子空间。
设噪声子空间为UN,由经典空间谱理论可知,理想条件下数据空间中的信号子空间与噪声子空间是相互正交的,即信号子空间中的导向矢量也与噪声子空间正交,则有下式成立:
(13)
任取e∈UN,由以上分析可知,有等式aH(θ,φ,γ)e=0成立,则任取e∈UN2⊂UN,有aH(θ,φ,γ)e=0成立,则有信号子空间中的导向矢量也与噪声子空间的子空间UN2正交,即:
(14)
UN2的维数等于极化敏感阵列包含的偶极子对个数,与入射信源数无关,则若用UN2来近似噪声子空间,可以实现未知信源数情况下的DOA信息和极化信息的联合估计。
与经典MUSIC算法相同,由于噪声的存在,a(θ,φ,γ)与UN2并不能完全正交,也就是说式(14)只能近似成立,所以构造DF-MUSIC算法的谱估计公式为:
(15)
根据子空间正交原理,在三维空间搜索,可得DOA信息及极化信息为:
(16)
2.2算法步骤总结
根据以上理论分析,将文中算法的步骤总结如下:
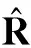
步骤4在信号参数范围内根据式(15)进行谱峰搜索;
步骤5找出极大值对应的角度及极化信息可得信号入射方向及其极化信息。
2.3算法运算量分析
在实际工程应用中,运算复杂度是衡量算法是否满足实时性要求的重要指标之一,因此本节对文中算法(DF-MUSIC)与经典基于长矢量的MUSIC算法的运算复杂度进行分析对比。MUSIC类算法的计算量主要体现在协方差矩阵的构造、特征值分解及谱函数的搜索过程。对比的两种方法采用了相同的协方差矩阵构造及特征值分解方法,因此运算量的区别主要体现在谱函数的搜索过程,而MUSIC类算法的运算量大部分都来自谱函数搜索过程,因此减少谱函数搜索过程的运算量可以极大的减少整个算法的运算量。下面对两种方法的谱函数搜索的运算量进行对比。
设入射源数为K,阵列是由M×M对正交偶极子构成的均匀平面矩形阵列,根据式(14)可知文中算法(DF-MUSIC)计算每一个搜索点的谱值的计算量为4M4+2M2,而经典的基于长矢量的MUSIC(LV-MUSIC)算法计算每一个搜索点的谱值的计算量为8M4-4M2K+2M2,文中算法与LV-MUSIC算法相比,每计算一个搜索点的谱值减少的计算量为Δ=4M4-4M2K=4M2(M2-K),而文中算法和LV-MUSIC算法都是以假设入射信源个数小于接收阵元数为前提推导得出的,即均需满足M2>K,则有Δ>0。计算空间谱包含方位角、俯仰角和极化辅助角三维信息,需要在这个三维空间进行极大值搜索。假设方位角搜索步数为nθ,俯仰角搜索步数为nφ,极化辅助角搜索步数为nγ,则共有nθnφnγ个搜索节点。则在构造空间谱这一步骤时采用文中算法比采用经典LV-MUSIC算法减少的计算量为nθnφnγΔ=nθnφnγ4M2(M2-K)。
综上所述,在两种算法的搜索空间及搜索步数相同的情况下,运算复杂度对比可以归纳为如表1所示。
3计算机仿真分析
为了验证文中算法的估计性能,对文中算法进行仿真分析。仿真采用由3×3对正交偶极子构成的均匀平面矩形阵接收信号,采样快拍数L设为200。假

表1 两种算法运算复杂度对比
设入射信号均为远场窄带横电磁波,且各入射信号之间相互独立。噪声的均值为零的空间加性白噪声。
实验1算法有效性验证
设信噪比SNR=10,两个入射信号到平面天线阵列的DOA参数(θ,φ)分别为(15°,45°)和(150°,60°),极化辅助角为10°和45°。图2和图3分别给出了极化辅助角为10°和45°时的空间谱图。
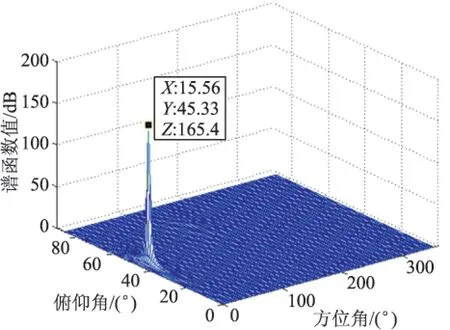
图2 极化辅助角为10°时DF-MUSIC算法的空间谱图
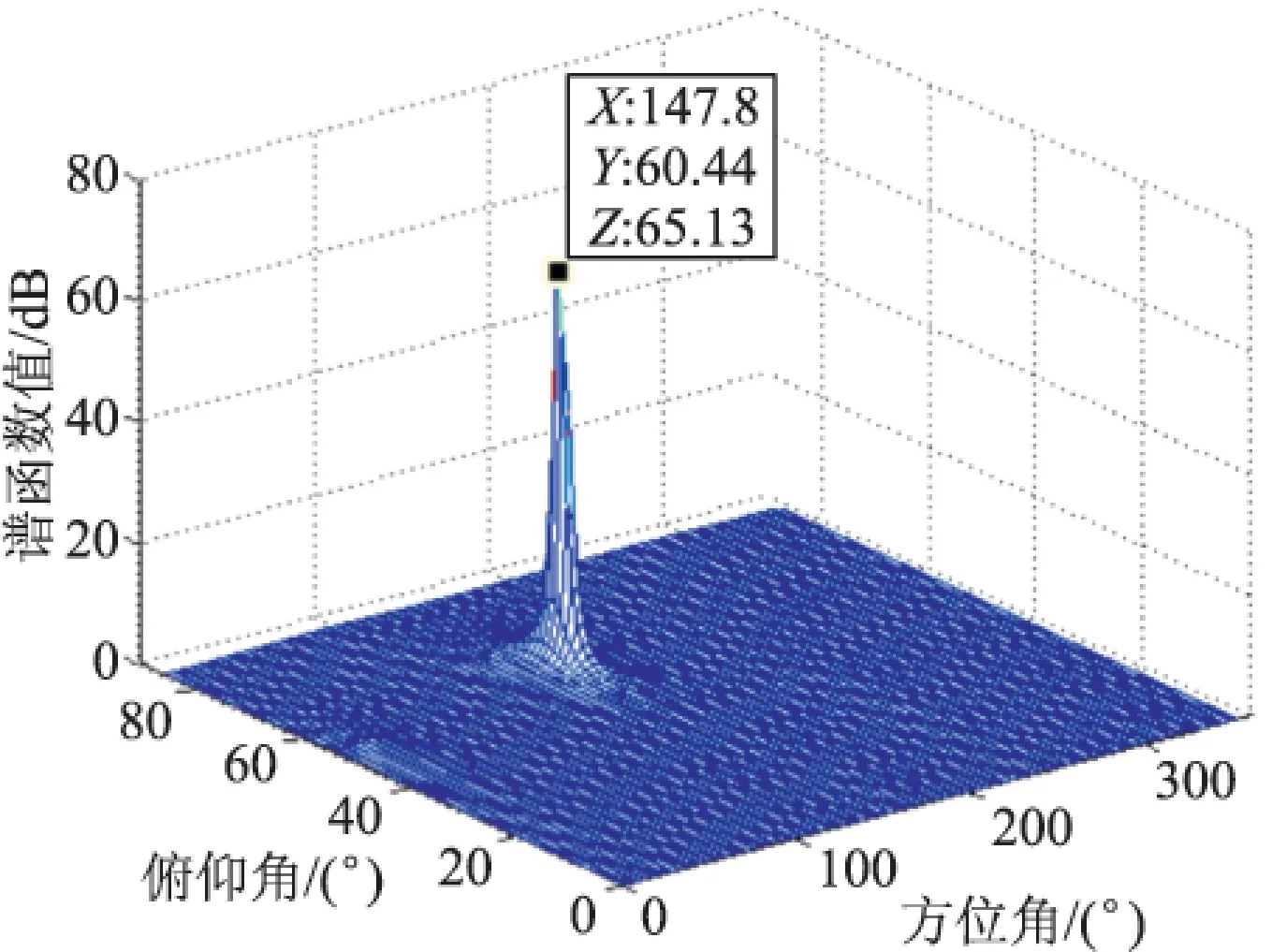
图3 极化辅助角为45°时DF-MUSIC算法的空间谱图
由图2和图3可见:DF-MUSIC算法可以有效估计出入射信号的DOA信息和极化信息,并且得到的空间谱图在入射信号点处的谱峰十分尖锐。这是因为算法采用了极化敏感阵列,接收的极化信息为信号参数估计提供了更多的信息量,有效改善了算法的估计性能。
实验2算法估计性能与信噪比的关系
下面通过仿真对DF-MUSIC算法和LV-MUSIC算法的估计精度进行对比分析。入射信号的DOA参数和极化参数的设置与实验1相同,设快拍数为100,信噪比SNR以2dB为步进值依从-2dB增加到20dB,噪声为空间加性高斯白噪声,进行100次独立重复实验。采用待估计参量的均方根误差来衡量算法的估计性能,定义待估计参量x的均方根误差的表达式为:
(17)
其中M为独立重复实验次数。仿真结果如图4~图6所示。

图4 对两入射信号方位角θ估计的RMSE随SNR的变化
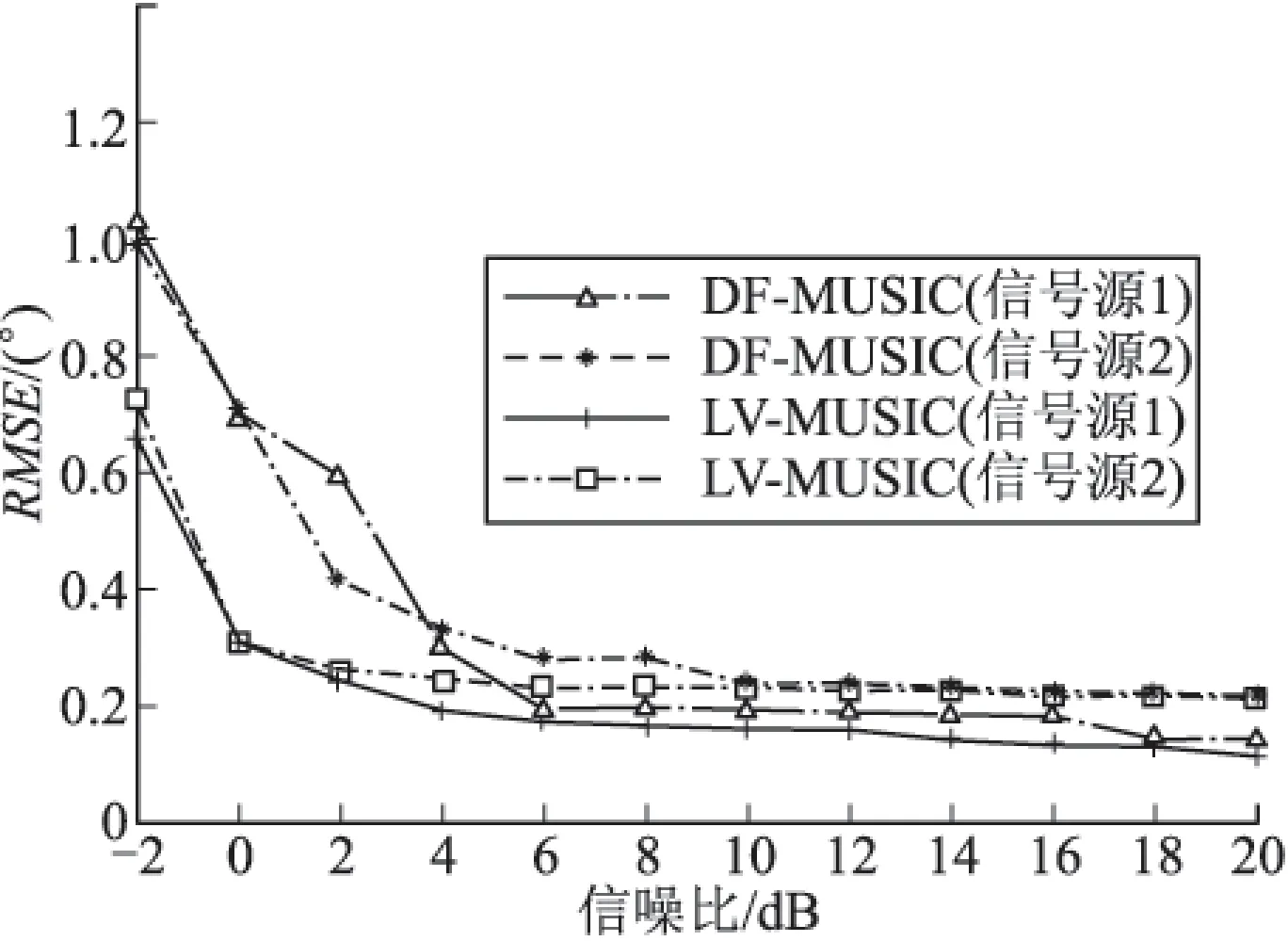
图5 对两入射信号俯仰角φ估计的RMSE随SNR的变化

图6两入射信号极化辅助角γ估计的RMSE随SNR的变化
从图4、图5和图6可以看出,随着信噪比的增加,两种算法对信号入射方位角、俯仰角及极化辅助角的估计误差均变小,即信噪比越大,估计精度越高。由图4可知,两种算法对入射信号方位角的估计误差几乎相同,而对信号源1方位角的估计误差明显大于对信号源2方位角的估计误差,这是由于信号源1的方位角设为150°,入射方向与天线阵成钝角,天线阵对信号的接收效果不及入射方向与天线阵成锐角的情况。而在入射方向与天线阵成锐角的情况下,对入射信号源2的方位角的估计误差在低信噪比时,LV-MUSIC算法的估计精度高于DF-MUSIC算法,但当信噪比增加到2dB以后,二者的估计精度相同。从图5可以看出,在低信噪比时,DF-MUSIC算法的估计精度低于LV-MUSIC算法的估计精度,随着信噪比的增加,二者的差别逐渐变小,并且估计误差趋于稳定。与对方位角和俯仰角的估计结果类似,同样是在低信噪比的情况下,DF-MUSIC算法的估计精度低于LV-MUSIC算法,随着信噪比的增加,二者的估计误差越来越接近。通过对仿真结果的分析可知,在低信噪比的情况下,文中算法的估计精度不及LV-MUSIC算法,但对方位角、俯仰角和极化辅助角的估计误差相差分别不超过0.5°、0.3°、1.2°,对于空间域的两个参量可以满足大多数的工程要求,而极化域的参量一般用于判断信号的极化状态,例如判断信号是水平极化还是垂直极化,仅需要知道信号的极化参量是在哪个区间内就可以满足工程需求,因此文中算法对信号的极化参量进行估计的估计精度同样满足工程指标。并且在同样满足工程需求的前提下,所提算法可以有效降低算法运算量。
4总结
文中基于传统的长矢量数据模型,利用噪声子空间维度特性提出了适用于极化敏感阵列的信号空间域极化域联合参数估计算法。算法对极化敏感阵列接收数据的协方差矩阵的特征值及特征向量进行分析,给出噪声子空间的近似形式,利用该近似形式构造空间谱,降低了生成空间谱时参与乘法运算的矩阵的维度,从而降低计算量。由于生成空间谱时根据各维度搜索步数的不同会导致需要计算的点数不同,因此各维度的搜索步数越大,所提算法较LV-MUSIC算法的运算量减少的就越多。而搜索步数越大,搜索间隔就越小,对应的估计精度越高,因此文中算法可以在保证估计精度的前提下减少一定的计算量。需要补充的是,文中算法的噪声子空间的近似形式并不拘于文中所提的方法,其适用于任何基于极化敏感阵列的噪声子空间类参数估计算法。
参考文献:
[1]庄钊文, 徐振海, 肖顺平, 等. 极化敏感阵列信号处理 [M]. 北京: 国防工业出版社, 2005: 199-213.
[2]张亮, 徐振海, 吴迪军, 等. 相干源诱偏下极化对相位干涉仪导引头测角影响研究 [J]. 电波科学学报, 2012, 27(4): 685-690.
[3]MIRONS,BIHANHL,MARSJI.Quaternion-musicforvector-sensorarrayprocessing[J].IEEETransactionsonSignalProcessing, 2006, 54(4): 1218-1229.
[4]王毅, 陈伯孝, 杨明磊, 等. 分布式nested阵列及其高精度DOA估计 [J]. 系统工程与电子技术, 2015, 37(2): 253-258.
[5]郑桂妹, 陈伯孝, 吴渤三. 正交分离式极化敏感阵列的波达方向估计 [J]. 电子与信息学报, 2014, 36(5): 1088-1093.
[6]WONGKainamThomas,ZOLTOWSKIMichaelD.Closed-formdirectionfindingandpolarizationestimationwitharbitrarilyspacedelectro-magneticvector-sensorsatunknownlocations[J].IEEETransactionsonAntennasandPropagation, 2000, 48(5): 671-681.
[7]WONGKT,ZOLTOWSKIMD.Self-initiatingMUSIC-baseddirectionfindingandpolarizationestimationinspatio-polarizationalbeamspace[J].IEEETransactionsonAntennasandPropagation, 2000, 48(8): 1235-1245.
[8]SOOKNUANT,SULEESATHIRAR.JointestimationofDOAandangularspreadusingpolarizationcomplexMUSIC[C]∥Proceedingsofthe2004InternationalSymposiumonCircuitsandSystems, 2004: 113-116.
[9]XUYou-gen,LIUZhi-wen,YAOGuang-xiang.Uni-vector-sensorSOS/HOS-CSSforwide-bandnon-Gaussiansourcedirectionfinding[C]∥Proceedingsofthe2005InternationalSymposiumonMicrowave,Antenna,PropagationandEMCTechnologiesforWirelessCommunications, 2005: 855-858.
[10]YUANQiao-wei,CHENQiang,SAWAYAKunio.MUSICbasedDOAfindingandpolarizationestimationusingUSVwithpolarizationsensitivearrayantenna[C]∥ProceedingsoftheIEEERadioandWirelessSymposium, 2006: 339-342.
[11]ZHOUMing,ZHANGXiao-fei.JointestimationofangleandpolarizationforbistaticMIMOradarwithpolarizationsensitivearrayusingdimensionreductionMUSIC[J].WirelessPersonalCommunications, 2015, 161(4): 137-143.
[12]GUOWeina,YANGMinglei,CHENBaixiao,etal.JointDOAandpolarizationestimationusingMUSICmethodinpolarimetricMIMOradar[C]∥IETinternationalConferenceonRadarSystems(Radar2012),Glasgow,Radar, 2012:1-4.
[13]李京书, 建武. 信号DOA和极化信息联合估计的降维四元数MUSIC方法 [J]. 电子与信息学报, 2011, 33(1): 106-111.
*收稿日期:2015-04-02
基金项目:航空科学基金(201401P6001)资助
作者简介:吴娜(1986-),女,黑龙江哈尔滨人,博士研究生,研究方向:宽带信号检测、处理与识别。
中图分类号:TN911
文献标志码:A
DimensionFeature-basedTwo-dimensionalDOAandPolarizationEstimationwithaPolarizationSensitiveArray
WUNa,SIWeijian,JIAOShuhong
(CollegeofInformationandCommunicationEngineering,HarbinEngineeringUniversity,Harbin150001,China)
Abstract:Joint estimation of DOA and polarization with a polarization sensitive array has the shortcoming of high computational complexity. In order to solve this problem, a direction of arrival (DOA) and polarization joint estimation algorithm based on dimension feature of the noise-subspace using polarization sensitive array was proposed. Approximation of projection matrix was obtained for construction of spectrum function by dimension feature of noise subspace, which reduces computational complexity of DOA and polarization joint estimation algorithm but also guarantees estimation performance. Ccomputational complexity of the algorithm was compared with that of long vector-based MUSIC algorithm. Finally, efficiency of the proposed algorithm was verified based on the simulation results.
Keywords:polarization sensitive array; dimension feature; DOA estimation; polarization estimation

