基于CFD尾翼稳定可控枪弹气动特性分析*
张成卿,王惠源,国海广,高树华
(1 中北大学,太原 030051;2 63936部队,北京 102200;3 重庆嘉陵特种装备有限公司,重庆 400032)
基于CFD尾翼稳定可控枪弹气动特性分析*
张成卿1,王惠源1,国海广2,高树华3
(1中北大学,太原030051;263936部队,北京102200;3重庆嘉陵特种装备有限公司,重庆400032)
摘要:为了优化可控枪弹结构,对可控枪弹整体结构进行简化处理,用三维软件SolidWorks布尔运算建立数值仿真模型,ICEM CFD生成非结构网格,通过Fluent对可控枪弹外流场数值仿真,得出不同马赫数不同攻角下阻力系数、升力系数、俯仰力矩系数以及压力中心系数变化规律。结果表明,可控枪弹气动特性处于静态稳定临界点,与试验结果相符,需要通过改变弹丸质心或者外形结构以优化结构。
关键词:可控枪弹;空气动力分析;外流场;静态稳定;Fluent
0引言
精确制导技术在中大口径炮弹及导弹已成熟应用,然而在枪弹的应用依然处于研究和试验阶段[1]。因此,提出一种尾翼稳定可控枪弹结构。
弹丸外形设计的优劣直接影响弹丸飞行稳定性及作战效能[2]。
弹丸稳定一般采用旋转稳定和尾翼稳定,判断弹丸稳定的一般方法是静稳定储备量的大小[3]。传统弹丸外形设计方法,对不同设计方案在风洞试验或者靶场试验分析前提下,得出最优结构方案[4],该方法周期长、效率低等缺点,使其已经不能适应现代武器的设计要求。数值仿真在一定程度上可以代替风洞试验,具有极强流场分析能力,可用于气动力设计及气动特性参数计算[5]。
文中采用Fluent对可控弹丸进行数值仿真,并分析仿真结果,能够体现弹丸流场特性,并且与试验结果吻合,为方案优化设计提供理论依据。
1尾翼稳定枪弹气动力学特性
按照空气学理论,对于尾翼稳定不旋转弹丸气动力学分析如图1所示[6]。

图1 总气动力示意图
OXYZ为弹丸运动坐标系,C表示弹丸质心,D表示弹丸压力中心,压力中心D到质心的距离为ld。
分析弹丸气动力学,可得:
(1)
(2)
(3)
式中:ρ为空气密度;ν为弹丸飞行速度;l为全弹长;Cx(Ma,δ)为阻力系数;Cy(Ma,δ)为升力系数;mz(Ma,δ)为俯仰力矩系数。
气动力系数Cx(Ma,δ)、Cy(Ma,δ)与弹丸的外形结构、飞行马赫数以及攻角有关。

(4)
(5)
Mz=Ryldcosδ+Rxldδ≈Ryld+Rxldδ
(6)
(7)
比值叫做静稳定度(压力中心系数),称为“稳定储备量”,静态稳定度主要反映弹丸的静态稳定性;多数情况下,即可得下式:
(8)
2仿真分析
2.1模型建立及网格生成
弹丸三维模型如图2所示,弹长138 mm,直径为12.7 mm,主要包括上弹体、下弹体、尾翼以及舵机等四部分。

图2 弹丸三维结构
为了在Fluent中进行仿真,对可控枪弹三维结构进行简化处理,在Solidworks中将枪弹建成弹丸模型(如图3所示),并且求出枪弹的质心;枪弹进行外流场分析,近似其为圆柱细长体,故在Solidworks中将计算域建成长圆柱体,长度为枪弹全长的6倍,直径为枪弹直径30倍,采用布尔运算生成计算区域;然后导入到ICEM CFD中进行网格划分,并将枪弹针体结构进行网格细化,生成非结构网格,弹丸CFD有限元仿真模型如图4所示。

图3 弹丸模型

图4 弹丸CFD有限元仿真模型
2.2初始条件和边界条件
取无限远处来流作为来流的初始条件,外边界取压力远场条件,用给定的自由流马赫数和湍流无限远处自由流的条件。
假设来流为理想条件,来流的攻角δ为0°~8°,来流马赫数为0.3~3。
2.3气动力学系数求解
Fluent求解后,可以得到流场内每个网格点上的流动参数:压力P,密度ρ等。将可控弹丸表面气动参数进行积分,得到总气动力F,然后分别向坐标系的X、Y、Z轴分解,得到3个方向上的载荷分量,求出气动力学各个系数。
2.4计算结果
气体的工作区域为400 mm×800 mm,ICEM CFD中生成的网格数为584 361个;气动力系数仿真结果如表1所示,1.3Ma时0°~8°攻角弹丸表面气流速度云图如图5所示;8°攻角时0.3~3Ma弹丸表面气流速度云图如图6所示。
2.4.1可控枪弹阻力特性分析
对仿真数据拟合,得出不同马赫数下阻力系数随攻角变化曲线(如图7所示)和不同攻角下阻力系数随马赫数变化曲线(如图8所示)。
由图8可以看出,马赫数大概在1.3左右时,阻力系数达到最大值;在阻力系数达到最大值之前,随着马赫数的增大而增大; 在阻力系数达到最大值之后,随着马赫数的增大而减小;在同一马赫数情况下,阻力系数随攻角的增大而增大;可控枪弹阻力系数曲线符合尾翼稳定弹丸空气动力特性。
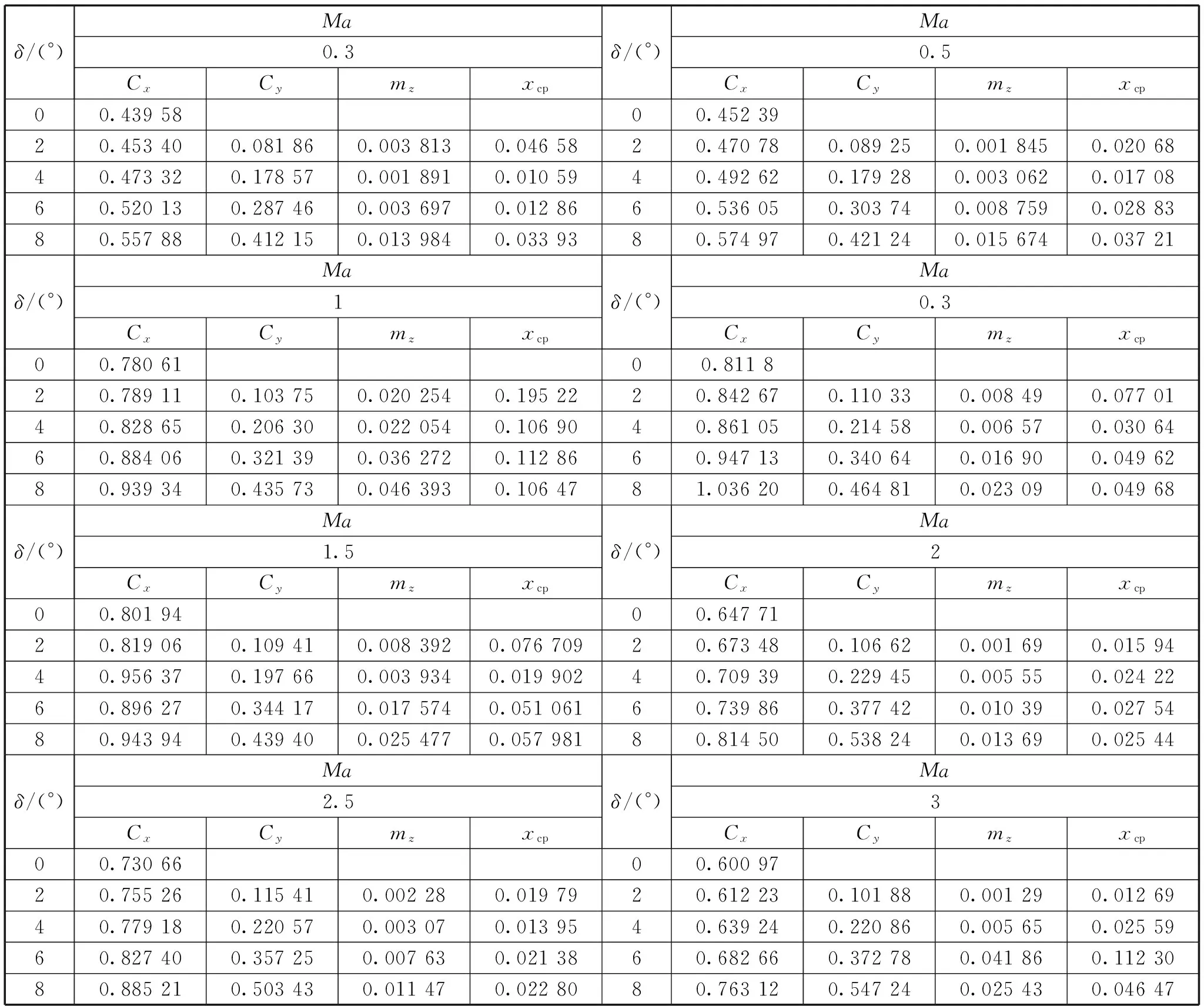
表1 可控弹丸气动力系数仿真结果

图5 1.3 Ma时不同攻角弹丸表面气流速度云图
2.4.2可控枪弹静态稳定性分析
Mz计算是以枪弹质心为力矩参考点,参考长度为枪弹全长0.15 m,参考横截面积为枪弹最大面积0.000 126 72 m2,根据式(8)即可计算出稳定储备量,如表2所示。
由表2可知,在1Ma时,可控弹丸稳定储备量最大,范围在10%~19%;在亚音速和超音速情况下,稳定储备量很低,范围在1%~50%;因此可知,在这种情况下,弹丸处于临界稳定处。高速摄影照片如图9和图10所示,图9弹丸出膛口瞬间弹丸弹头前部明显上抬;图10弹丸出膛口瞬间弹丸弹头基本处于水平飞行;因此可知弹丸处于临界稳定性;即仿真结果与试验结果吻合。
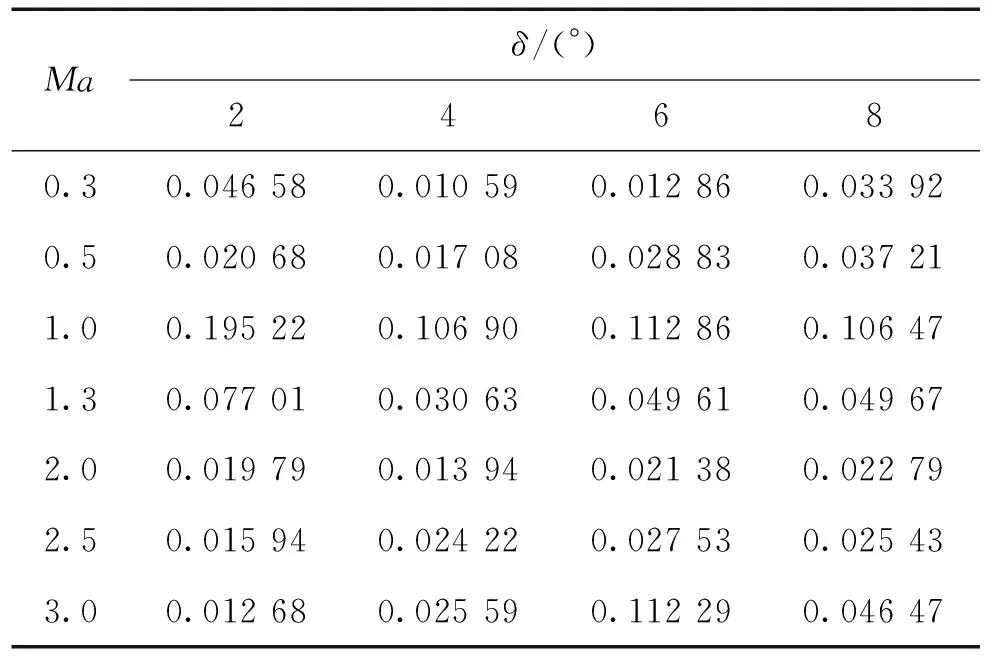
表2 稳定储备量表

图6 攻角为8°时不同马赫数弹丸表面气流速度云图
3结论
利用Fluent对大口径尾翼稳定可控弹丸气动力学仿真计算,可得气动力学参数,用所得结果分析弹丸稳定性,得出弹丸稳定性处于临界条件,与靶场试验结果相符。因此,弹丸整体结构需要进一步结构优化,改进弹形结构或者质心。
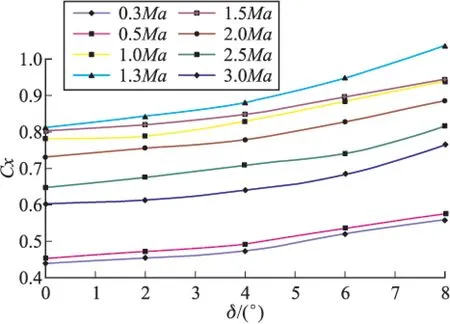
图7 攻角-阻力系数曲线
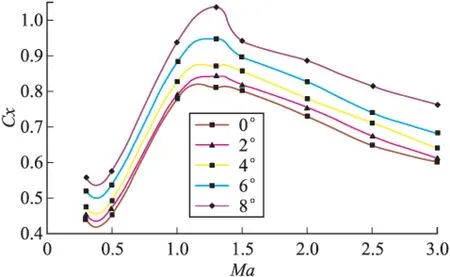
图8 马赫数-阻力系数曲线

图9 弹丸膛口飞行姿态

图10 弹丸膛口飞行姿态
参考文献:
[1]杨绍卿. 灵巧弹药工程 [M]. 北京: 国防工业出版社, 2010: 3-6.
[2]韩子鹏. 弹箭外弹道学 [M]. 北京: 北京理工大学出版社, 2008: 25-41.
[3]孙宜亮. 子弹飞行稳定性 [D]. 南京: 南京理工大学, 2009.
[4]王保国, 刘淑艳, 黄伟光, 等. 气体动力学 [M]. 北京: 北京理工大学出版社2008, 5: 50-56.
[5]苗瑞生, 居贤铭, 吴甲生, 等. 导弹空气动力学 [M]. 北京: 国防工业出版社, 2008, 6: 85-90.
[6]徐明友. 火箭外弹道学 [M]. 哈尔滨: 哈尔滨工业大学出版社, 2004: 64-68.
[8]王良明. 尾翼式柔性弹箭飞行稳定性研究 [J]. 弹道学报, 1998, 10(4): 67-73.
[9]刘万刚, 高宏超, 叶正寅, 等. 细长弹箭自由飞行状态下的静气动弹性分析 [J]. 航空制造技术, 2011(19): 107-108.
[10]TALAYTheodoreA.IntroductionAerodynamicsofFlightNASA.SP-367 [R].NationalAeronauticsandSpaceAdministrtion,Washington,D.C. 1975.
*收稿日期:2015-03-30
作者简介:张成卿(1988-),男,山西运城人,博士研究生,研究方向:高射速发射理论与技术研究。
中图分类号:TJ410.3
文献标志码:A
Aerodynamic Analysis for Fin-Stabilized Smart Bullet Based on CFD
ZHANG Chengqing1,WANG Huiyuan1,GUO Haiguang2,GAO Shuhua3
(1North University of China, Taiyuan 030051, China; 2No.63936 Unit, Beijing 102200, China;3Chongqing Jialing Special Equipment Co. Ltd, Chongqing 400032, China)
Abstract:To optimize bullet design, Solidworks was used to simplify overall structure of bullet and establish numerical simulation with Boolean operation, ICEM CFD generated mesh of this model, and simulation was performed by Fluent for outer flow field to obtain drag coefficient, life coefficient, pitching moment coefficient and center of pressure coefficient at different angles and different Mach number. The result shows that the aerodynamic characteristics of a controlled bullet are in critical point for statically stable, which is consistent with the test results, so it is need to optimize the structure by changing the shape or structure of the projectile centroid.
Keywords:smart bullet; aerodynamic analysis; outer flow field; static stability; Fluent

