导弹喷焰流场与凝结尾迹的工程计算方法*
郭 琼,蔡 猛,靖建全,周德召
(1 洛阳电光设备研究所,河南洛阳 471009;2 北京理工大学宇航学院,北京 100081)
导弹喷焰流场与凝结尾迹的工程计算方法*
郭琼1,蔡猛1,靖建全2,周德召1
(1洛阳电光设备研究所,河南洛阳471009;2北京理工大学宇航学院,北京100081)
摘要:为快速预估飞行器喷焰流场及其在一定空域内产生的凝结尾迹,为飞行器目标红外辐射研究提供条件,采用一种工程模型对含复燃效应和水汽凝结效应的喷焰流场进行计算分析。模型以燃气射流的一维流动理论、湍流混合以及化学平衡条件为基础建立控制方程,并采用四阶Runge-Kutta方法进行求解计算。模型校验和分析表明,该工程计算方法能够获得喷焰流场射流区的典型参数,并具有较高的计算效率。
关键词:喷焰流场;凝结尾迹;复燃;工程计算
0引言
随着火箭导弹技术的发展,各种类型和用途的火箭导弹应运而生,相应地通过尾喷焰获取光学辐射特性来识别、捕获和追踪目标成为一种重要手段[1]。而认识和研究火箭导弹飞行过程中的喷焰流场状态,是进行尾喷焰辐射特性分析的基础,国内外均采用实验方法和数值计算方法开展了大量研究[2-3]。利用二维或三维计算流体力学方法(CFD)计算发动机喷焰能够获得完整的流场分布和组分信息,计算精度较高,得到了广泛应用[4]。但由于CFD方法计算量大,计算周期长,在分析不同高度、不同飞行状态的喷焰流场时,计算效率较低。因此发展能够快速估算喷焰流场特性和组分分布的工程模型和计算方法,对进行大量工程应用的分析具有重要的价值和意义。
这里结合喷焰流场的流动特征,利用喷焰流场与环境大气的湍流混合过程、一维流动理论和化学平衡条件,建立了喷焰流场快速计算的工程模型。与此同时,结合尾喷焰中水汽的凝结机理,建立了一种估算凝结尾迹的计算方法。模型校验和分析表明,采用工程算法不但能够获得一定精度的喷焰流场结果,其计算效率也能大大提高。
1计算模型
1.1简化与假设
在满足连续介质假设的大气层内,由于火箭发动机喷出的超声速燃气射流与环境大气相互作用和掺混,会出现复杂的流场结构和流动现象。在喷管出口附近,高速喷出的燃气射流由于压强、密度和速度等与环境大气不同,形成复杂的马赫波系结构,研究中通常将这一包含复杂波系结构的区域称为初始区;在喷管出口下游一段距离,燃气与环境大气相互掺混,未燃尽组分与氧气混合后产生复燃,对组分和流场分布产生显著影响,研究中将这一区域称为射流区;在初始区和射流区中间为过渡区,如图1所示。
本研究采用的工程模型中,为考虑模型的真实物理效应而又不失简单性,主要针对尾喷焰的射流区进行建模和计算,并考虑湍流卷吸效应、复燃效应、射流扩张以及伴随流影响等。工程模型满足如下简化和假设条件:
1)来自于环境大气的卷吸质量流一经吸入就在射流面上均匀混合;
2)喷焰在射流区内是等压发展,其压强与环境大气压强一致;
3)在初始区和过渡区既没有卷吸效应也没有化学反应的产生。
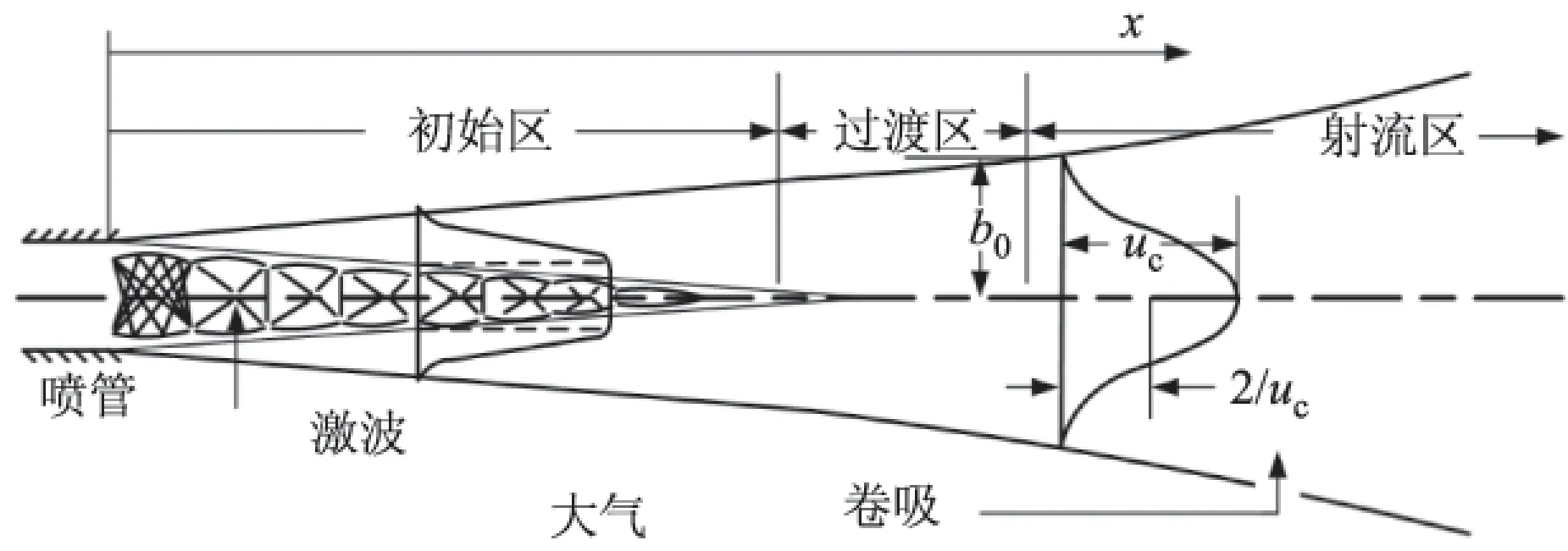
图1 喷焰流场结构示意
1.2喷焰模型方程
工程模型的基本方程参照Woodroffe[5]在1975给出的一维喷焰流场控制方程建立,包含质量守恒方程、动量守恒方程、能量守恒方程、组分守恒方程、复燃模型方程等。
考虑射流区任意微小分段dx的控制体,依据射流流动过程中流进和流出控制体的质量流量、周围空气卷吸进入射流区的质量流量等,可建立控制体内质量流量的变化方程为:

同质量流量的变化类似,控制体的动量守恒表达式为:
结合质量通量和动量通量的关系,易得控制体内的能量变化包括控制体内剩余燃料的燃烧生成热和来自卷吸效应的来流能量,控制体内的能量守恒关系式为:

其中:yi为射流中组分i的质量分数;yi∞为环境大气来流中组分i的质量分数。
对于具有Nr个基元反应的某反应,其当量表达式可以写为:
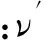
1.3水汽凝结模型
通常情况下,发动机尾喷焰包含大量的由推进剂燃烧生成的水汽,尾喷焰在与环境大气的湍流掺混过程中,尾喷焰气流温度不断降低,相应的饱和水汽压强不断降低,大量水汽从喷焰中析出并凝结为微小液滴或冰晶。由于喷焰中通常包含碳黑或其它粒子,水汽凝结具有丰富的凝结核,因此在模型中不考虑凝结核条件,而只考虑饱和水汽压随温度的变化。
尾喷焰的发展采用上述工程模型进行描述,并引入如下假设描述水汽凝结状态:
1)忽略水汽凝结的时间历程,当尾喷焰发展过程中水汽压一旦超过饱和水汽压,超出部分水汽全部析出并凝结;
2)假定水汽凝结均产生微小液滴,不考虑产生冰晶的状态。
基于上述假设,对于尾喷焰发展过程中的某一微小区域,当其水汽的质量分数为yg,当地压强为p,密度为ρ,液滴密度为ρl,液滴直径为dl饱和水汽压为pa,则在当地产生凝结的水汽质量分数、体积分数和数密度分别为:
1.4模型方程的求解
为求解尾喷焰的工程计算模型,需要依据喷口的流动参数获得射流区入口截面上的流动参数作为初始条件。根据喷焰流场工程模型的假设条件,认为初始区和过渡区内喷焰没有卷吸效应和复燃化学反应,则从喷管出口至射流区入口位置的守恒关系进行匹配可获得射流区的初始参数。
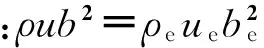


组分守恒:y0i=yei
式中:下标e表示喷管出口参数;CD为射流阻力系数。由于喷焰流场的基本方程为一阶微分方程组,在确定初值情况下,可采用四阶Runge-Kutta方法进行求解计算。
2模型验证与分析
2.1模型的校验
为验证工程计算模型,利用王伟臣[6]研究中给出的条件进行了喷焰流场的计算,获得结果与文献中的温度和速度对比如图2所示。可以看出两种模型在射流段的温度变化趋势基本一致,数据误差小于10%。二者的速度变化趋势基本一致,在0.6 m≤x≤0.7 m之间,即射流初始段部分差异较大,这主要是射流初始位置与实际位置存在差异的缘故;在0.7 m之后,工程模型与文献数据的速度差异保持在10%以内。
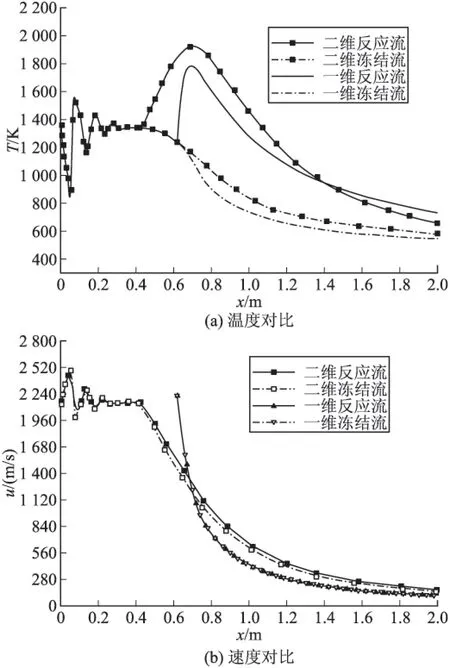
图2 工程模型(图中一维数据)与文献结果(图中二维数据)对比
3.2喷焰流场计算示例
利用上述工程计算方法,对国外某型导弹位于10 km高度,飞行马赫数为2时的喷焰流场进行示例分析。计算模型喷管出口直径为150 mm,喷口燃气压强为83 238 Pa,温度为1 088 K,速度为2 252 m/s,燃气比热比为1.18。喷口位置组分质量分数为:H2为0.042,N2为0.108,CO为0.48,CO2为0.0241,H2O为0.0115,HCl为0.199,其它为0.094。
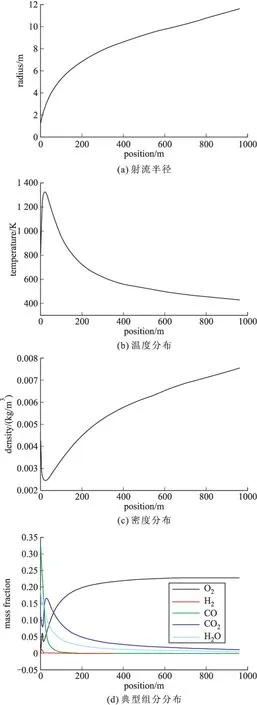
图3 示例模型的工程计算结果
图3给出了该示例模型射流区的半径、温度、密度和典型组分沿轴向的分布状态。从图中可以看出,在射流发展过程中,射流半径逐渐增加;在射流发展初期,射流半径增长较快;在300 m以后,射流半径相对较为平缓。在喷焰射流区发展初期,部分环境空气卷吸进入射流区内,与未燃尽组分发生复燃化学反应,因此这一区域内温度升高,H2、CO等组分质量分数快速降低,H2O和CO2组分浓度增加;此后随着卷吸气体的增加和射流的扩张,燃气组分与空气组分逐渐掺混,燃气组分浓度降低,空气组分浓度增加并趋于环境条件。
相关研究表明,喷焰流场射流区在发展过程中,其横截面上参数的径向分布具有自模性特征[7]。结合工程模型的计算结果,利用典型参数的径向参数自模性,可对其进行径向扩展。针对上述计算结果,近似取自模性分布为:
其中z为满足自模性条件的流场参数,如相对速度、剩余温度以及相对密度等。取zm为工程模型计算值时,可获得扩展后的喷焰射流区流场分布如图4所示。

图4 按自模性扩展后的射流区流场分布
在自模性扩展基础上,利用前述水汽凝结模型,可获得喷焰发展过程中凝结液滴的数密度如图5所示。在计算数密度时,假设液滴直径为10 μm。
示例模型计算时,在单核计算机上的计算时间为10 min,计算域范围自动扩展为20 m×1 000 m。如
同样模型采用基于轴对称模型的CFD方法进行求解计算,在单核计算机的计算时间超过120 h。
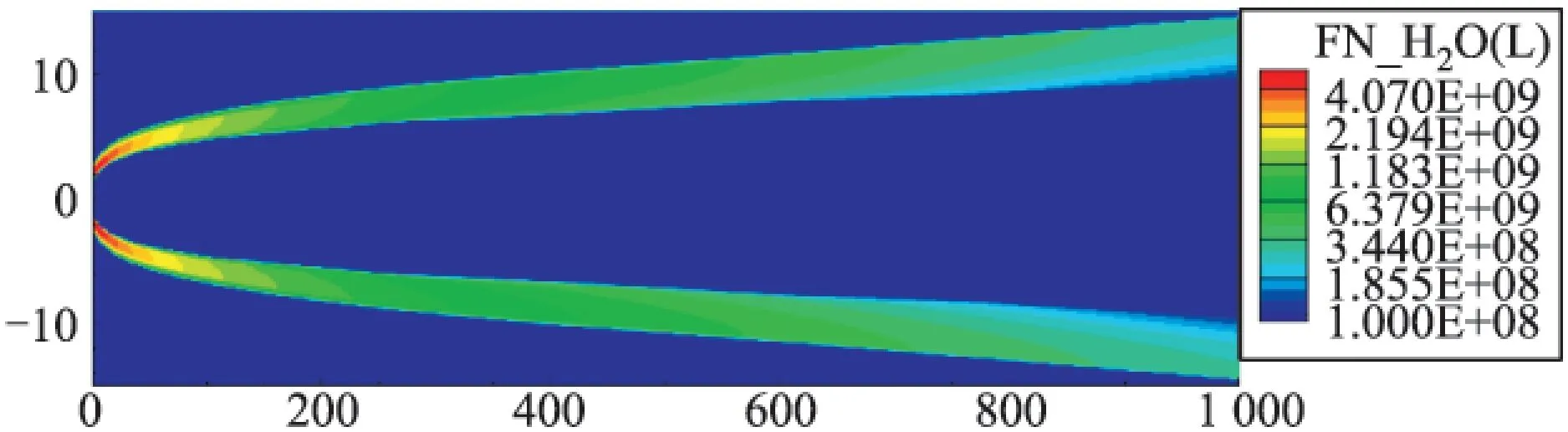
图5 水气凝结尾迹结果
3结论
研究结合喷焰流场特性和目标辐射特性计算需求,基于一维流动、湍流混合、化学平衡条件以及水汽凝结条件,建立了一种进行火箭发动机尾喷流射流区流场参数计算的工程计算方法。通过与公开文献的对比和计算示例分析表明,该方法能够获得尾喷焰的射流区参数,结果误差在工程计算能够接受的范围内;工程模型计算效率较高。此外,由于工程模型不需划分网格,可自动扩展计算区域,能够有效的在较大空间范围内进行喷焰流场计算,对作用范围很广的高空喷焰具有较好的计算分析能力。
参考文献:
[1]张术坤, 蔡静. 尾焰红外辐射特性计算研究综述 [J]. 激光与红外, 2010, 40(12): 1277-1282.
[2]王雁鸣, 谈和平, 董士奎, 等. 低空多喷管发动机喷焰红外特性研究 [J]. 固体火箭技术, 2009, 32(6): 634-637.
[3]国爱燕, 白廷柱, 胡海鹤, 等. 固体火箭发动机羽烟紫外辐射特性分析 [J]. 光学学报, 2012, 32(10): 168-175.
[4]姜毅, 傅德彬. 固体火箭发动机尾喷焰复燃流场计算 [J]. 宇航学报, 2008, 29(2): 225-229.
[5]WOODROFFE J. One-dimensional model for low-altitude rocket exhaust plumes: AIAA-75-224 [R]. 1975.
[6]王伟臣. 固体火箭发动机排气羽流红外特性研究 [D]. 北京: 北京理工大学, 2010.
[7]赵承庆, 姜毅. 气体射流动力学 [M]. 北京: 北京理工大学出版社, 1998: 81-84.
*收稿日期:2015-03-26
基金项目:空军装备预先研究项目(61901060601)资助
作者简介:郭琼(1978-),男,河南驻马店人,工程师,硕士,研究方向:系统仿真。
中图分类号:V411.3
文献标志码:A
An Engineering Calculation Method for Exhausted Jet Flow and Contrail
GUO Qiong1,CAI Meng1,JING Jianquan2,ZHOU Dezhao1
(1Luoyang Institute of Electro-optical Equipment, Henan Luoyang 471009, China;2School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)
Abstract:To predict exhausted jet flow and contrail in specific altitude from rocket engine efficiently, an engineering method was performed to calculate jet flow including afterburning and contrail effect. Control equations based on one-dimensional flow theory, turbulent mixing and equipment chemistry reaction were solved by the method of fourth-orders Runge-Kutta. Model verification and example prove that typical parameters of exhausted jet flow in the jet flow region could be achieved by this method, which is more computationally efficient.
Keywords:exhausted jet flow; contrail; afterburning; engineering calculation method

