复合固体推进剂交变温度载荷下的老化动力学*
王玉峰,黄卫东,李金飞,张旭东,隋玉堂
(海军航空工程学院,山东烟台 264001)
复合固体推进剂交变温度载荷下的老化动力学*
王玉峰,黄卫东,李金飞,张旭东,隋玉堂
(海军航空工程学院,山东烟台264001)
摘要:为考察复合固体推进剂在交变温度载荷条件下的老化动力学,揭示其老化机理,讨论了传统高温加速老化方法在处理复合固体推进剂交变温度加速老化试验数据时存在的局限性,建立了交变温度加速老化动力学模型,给出了等效温度和等效循环时间的计算方法和交变温度环境下活化能的计算公式,提出了复合固体推进剂交变温度载荷下的老化机理,使预估结果更符合实际贮存环境,相关性更好。
关键词:复合固体推进剂;交变温度;老化动力学;等效温度
0引言
复合固体推进剂自生产之日起将会经历生产、运输、贮存和使用环境的考验,这些环境因素对固体推进剂具有明显的不良影响,其中,温度是重要的影响因素,在其作用下,推进剂将发生老化,将导致其物理和化学性能变化[1]。温度影响推进剂化学反应速率,贮存温度越高,性能变化越快。温度对老化速率的影响一般用Arrhenius经验公式描述[2]。所以为了在较短的时间内了解固体推进剂的性能变化规律,都是采用高温加速老化方法[3],在高温加速老化试验的基础上,定期测试其力学性能,给出其力学性能随时间和温度的变化规律,再根据Arrhenius方程和物理老化数学模型,依据相关失效判据,外推至常温及使用环境下的贮存寿命。
许多学者[4-8]都通过高温加速老化法研究了复合固体推进剂的老化动力学和机理,利用Arrhenius公式建立了老化程度与推进剂贮存温度之间的关系。
目前高温加速老化试验中都是定常的试验和使用温度,温度是恒定的,预估的寿命也只针对定值温度。由于活化能是温度的函数(一般是温度越高,活化能越大)[9],但Arrhenius公式一般是用高温活化能作为常温活化能,这样就会引起较大误差,导致预估结果偏于保守,推进剂的预测寿命比实际寿命要短,到期的推进剂仍能使用。在现实条件下,贮存和使用温度是在很大范围内变化的[10],目前对固体推进剂在交变温度下的老化机理及寿命评估研究较少。因此开展固体推进剂在交变温度载荷下的寿命预估研究具有特殊的意义。
1老化模型
为预估推进剂的贮存寿命,首先必须建立推进剂老化过程中性能参数P与贮存温度T和贮存时间t的关系。根据测试数据的变化规律,选择适宜的描述性能变化的方程,一般有3种:
(1)
式中:t为时间;k为性能变化的速率常数;P0为初始性能;P为t时的性能。
k与温度T的关系符合Arrhenius公式,即:
(2)
2传统高温老化数据处理方法
将各个老化温度下通过式(1)求得的k值代入式(2)回归,求出A、Ea,从而可以得到常温下的速率常数k20,再将k20代入式(1),根据性能失效判据得到常温寿命t20[3]。
根据式(1)和式(2)有:
(3)
(4)
式中,τ和T为相应的时间和温度,在这样的时间和温度下所选的力学性能变化到某个值。
式(3)、式(4)对定常的试验和使用温度是正确的,但是在现实条件下,贮存和使用温度是在很大范围内变化的。
3交变温度加速老化动力学模型
交变温度载荷下推进剂的老化失效表现为伸长率的失效[11],选择伸长率作为推进剂失效参量,采用下式作为推进剂老化数学模型:
(5)
式中:εm(t)为老化时间t后的伸长率;t为老化时间;k为伸长率变化速率,是变温周期和温度幅值的函数;εm0为未经老化的推进剂的伸长率。
试验温度:
(6)
式中:T(t)为t时刻的温度;T0为初始温度;Tmax为温度上限值;Tmin为温度下限值;P为温度变化周期。
由于温度不断变化,由式(2)可知,k也是不断变化的,有:
(7)
对于连续的温度:
(8)
由Arrhenius反应速率式可知,在交变温度下:
(9)
式中:k(T)最大值为kmax=Ae-B/[T0+(Tmax-Tmin)/2];k(T)最小值为kmin=Ae-B/[T0-(Tmax-Tmin)/2];k(T)均值为kave=Ae-B/T0。
k(T)在kmax和kmin之间变化,如图1所示。

图1 退化速率
3.1等效温度和等效循环时间
1)等效温度
交变环境温度下,应该存在一个温度,即等效温度Te,在此温度下的老化性能程度与交变温度老化的作用效果是相当的。该等效温度对推进剂老化程度的作用等效于真实温度T=T(t)的作用。
将实际的交变温度区间用Δt分割,在Δt时间内实际上作用着一个温度Ti。
由于等效的贮存温度所引起的推进剂性能变化也应该是真实的可变量,因此,从方程(4)可以得到相应的关系式:
(10)
所以:
(11)
式中:te为指定的贮存和使用时间;Δti为区间平均温度为T1的温度区间(不大于5 K)的持续时间;Ea为活化能(温度系数,J/mol);R为气体常数,值为8.314 J/mol·K;Δτj为区间平均温度为Ti的温度区间(不大于5 K)的持续时间;Te为指定的条件下,按温度Ti的分布数据所计算出的等效温度。
2)等效循环时间
等效循环时间[12]是一个特征时间,是等温老化过程中等效于温度循环中相同的性能变化的时间。
由式(1)可将伸长率的变化改写为:
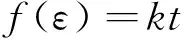
(12)
(13)
在等温老化条件下有:
(14)
进一步改写为:
(15)

在如图2所示的变温环境下,温度变化率为:
(16)
式(15)用积分表示为:
(17)
由式(15)和式(17)即可求得等效循环时间。
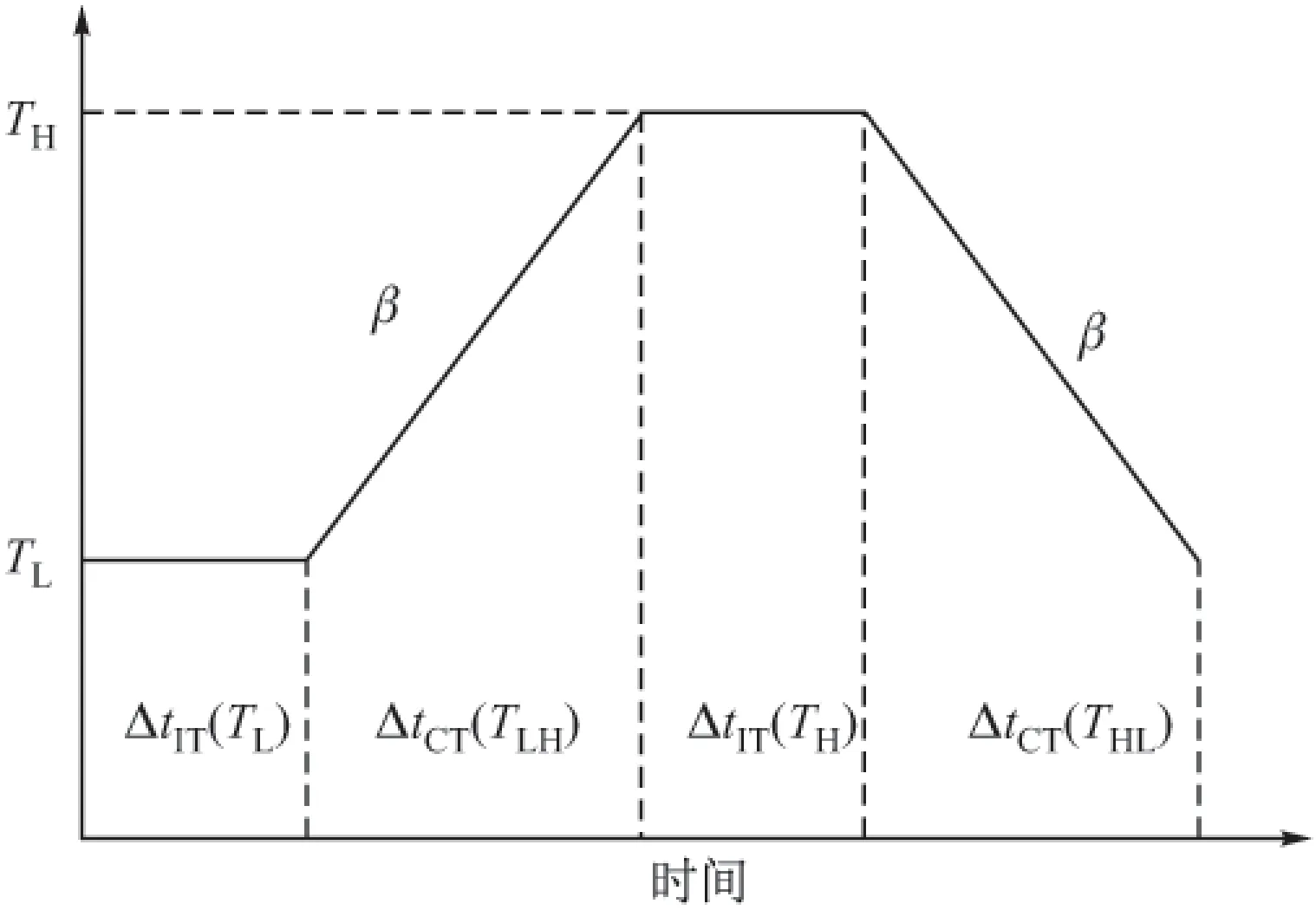
图2 温度循环示意图
式(17)可进一步改写为:
(18)
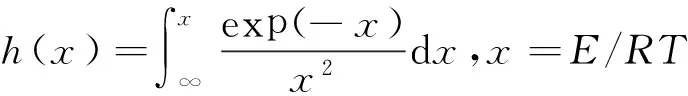
为进一步计算等效循环时间,取某一参考温度Tr,图2中的温度循环由等温和变温过程组成。
图3是等温过程的等效示意图。在等温TL下性能从ε1变化到ε2所需的时间是t2-t1,而相同的变化在参考温度Tr下所需的时间是ΔtIT,ΔtIT定义为Tr下的等效等温时间。同理,ΔtCT为动态升温过程中参考温度Tr的等效等温时间,如图4所示。
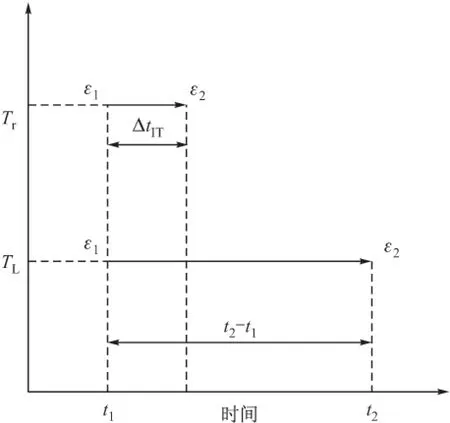
图3 等效恒温时间示意图
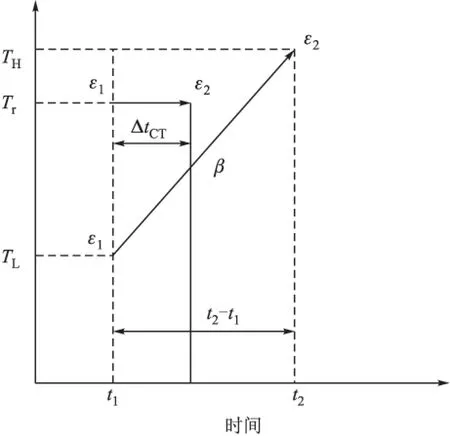
图4 等效循环时间
由图3可以看出,性能从ε1变化到ε2,可得:
(19)
由式(15),在Tr下有:
(20)
由式(19),在温度TL下达到相同的变化有:
(21)
由式(20)和式(21),可得TL等温阶段参考温度Tr的等效等温时间为:
(22)
由图4可将式(18)改写为:
(23)
由式(23)、式(20)得Tr的等效等温时间为:
(24)
式(22)、式(24)分别表示的是等温和动态升温过程的等效等温时间。
将温度循环过程中所有等效等温时间相加即可得到在参考温度Tr的等效循环时间,即:
(25)
式中,N为温度循环数。
3.2活化能的近似估计
根据范特霍夫近似规则,温度每升高10 K,反应速率大约增加2至4倍(取2.7),即:
(26)
而由Arrhenius方程可得加速系数为:
(27)
联立式(26)和式(27)可得:
(28)
两边求自然对数可得:
(29)
美国航天航空工业协会发布的最新标准[9]及文献[13]给出了温度加速寿命试验公式:
(30)
式中:HL为使用寿命;HT为加速贮存试验时间;T2为加速贮存试验温度;T1为正常贮存温度。
其加速系数为:
(31)
再根据式(27)可得:
(32)
两边取对数,有:
(33)
由于推进剂在不同的温度范围内,活化能也有一定的变化,上面两种方法求出的推进剂活化能应该都是正确的,相关文献[7]给出的推进剂的活化能为:低温时70 kJ/mol,高温时120 kJ/mol。文中计算的活化能都在合理的范围内,如图5、图6所示。从图中可以看出,当贮存温度是定常温时,活化能与贮存试验温度成线性关系。但对交变温度加速老化试验来说,其活化能是变化的。

图5 恒温下的活化能

图6 变温环境下的活化能
4固体推进剂的交变温度老化机理
交变温度对固体推进剂的老化效应主要是高温效应、低温效应和疲劳累积效应,如图7所示。

图7 交变温度效应示意图
1)高温效应
高温导致推进剂力学性能衰减,主要表现为老化等现象,其失效模式主要是结构完整性的破坏和因为相变而造成的永久性破坏。化学反应速率随温度升高而增加,因而增加了氧化的发生。高温老化将导致推进剂模量降低[14],交联密度降低,还有加速推进剂破坏的作用。
2)低温效应
诚然温度降低,推进剂老化降解反应减缓,但在更低的温度贮存时,会出现结晶现象,导致伸长率显著降低。低温环境对推进剂的机械性能有造成脆性破坏的趋势,当温度降低时,推进剂材料实际上是变得更硬,导致模量增加,交联密度增加,此时推进剂中高分子粘合剂处于玻璃化状态,高分子链在受到较大应力时才发生强迫高弹形变,有可能会导致伸长率提高,但随着老化时间的增加,高分子粘合剂逐渐老化,长的高分子链也会逐渐断裂成为短链,能发生强迫高弹形变的运动单元越来越少,分子间的相对滑移越来越多[15],导致其力学性能恶化。
3)疲劳累积效应
疲劳效应也促使推进剂降解老化,特别是当推进剂经受温度循环时,由于疲劳和高温老化的综合作用,其降解速率更快[16]。
5结论
通过以上研究,得到下述结论:
1)在交变环境温度下,存在一个等效温度,该等效温度下推进剂老化程度等效于真实温度作用的老化程度。
2)当贮存温度是定常温时,活化能与贮存试验温度成线性关系,活化能随温度的升高而升高。对交变温度加速老化试验来说,其活化能是变化的。所以,传统高温老化试验的数据处理中,以高温条件下得到的活化能作为常温时的活化能,是引起预估偏差的主要原因。
3)交变温度环境条件下,固体推进剂的老化机理主要表现在高温效应、低温效应和疲劳累积效应等方面。
参考文献:
[1]贺南昌. 贮存温度对丁羟推进剂老化性能影响的研究 [J]. 推进技术, 1987, 8(6): 58-63.
[2]MICHAEL D J. An investigation of composite propellant accelerated ageing mechanisms and kinetics [J]. Propellants, Explosives, Pyrotechnics, 2003, 28(3): 114-119.
[3]国防科学技术工业委员会. 复合固体推进剂高温加速老化试验方法: QJ 2328A-2005 [S]. 北京: 中国航天标准化研究所, 2005.
[4]BROUWER G R, KEIZERS H. Aging in composite propellant grains: AIAA 2004-4058 [R]. 2004.
[5]CUNLIFFE A V, DAVIS A, TOD D. Ageing and Life Prediction of Composite Propellant Motors: AGARD-CP-586 [R]. 1996.
[6]MARGETSON J, WONG F C. Service life prediction of solid rocket propellant motors stored in a random thermal environment: AGARD-CP-586 [R]. 1996.
[7]CELINA Mathew, MINIER Leanna, ASSINK Roger. Development and application of tools to characterize the oxidative degradation of AP/HTPB/Al propellants in a propellant reliability study [J]. Thermochimica Acta, 2002, 384(1/2): 343-349.
[8]KIVITY M G, HARTMAM A M A. Aging of HTPB Propellant: AIAA 2005-3802 [R]. 2005.
[9]YANG L C. Correlation between the accelerated aging test(AAT)and real world storage temperature: AIAA 2007-5138 [R]. 2007.
[10]王玉峰, 李高春, 王晓伟. 固体火箭发动机海洋环境下的贮存及寿命预估 [J]. 火炸药学报, 2008, 31(6): 87-90.
[11]王玉峰. 舰载导弹固体火箭发动机装药贮存寿命预估技术研究 [D]. 烟台: 海军航空工程学院, 2010.
[12]CHUNG K, SEFERIS J C, NAM J D. Investigation of thermal degradation behavior of polymeric composites: prediction of thermal cycling effect from isothermal data [J]. Composites: Part A: Applied Science and Manufacturing, 2000, 31(9): 945-957.
[13]赵婉, 韩天龙. 基于活化能的火工品加速贮存寿命试验优化设计方法 [J]. 含能材料, 2009, 17(4): 475-477.
[14]隋欣, 万谦, 王宁飞, 等. 高温老化过程中推进剂模量变化对装药结构完整性的影响 [J]. 推进技术, 2009, 30(3): 370-374.
[15]李松年, 刘勇, 王罗新, 等. HTPB推进剂储存老化性能试验研究 [J]. 推进技术, 2006, 27(5): 473-476.
[16]HARD W D, BRIGGS W E. Experimental and theoretical correlation of aging effects between laboratory and analog motors: AIAA68-527 [R]. 1968.
*收稿日期:2015-04-25
基金项目:武器装备预研基金资助。
作者简介:王玉峰(1978-),男,河南睢县人,讲师,博士,研究方向:固体发动机寿命预估。
中图分类号:V512
文献标志码:A
Aging Kinetics of Composite Solid Propellant Under Cycling Temperature Loading
WANG Yufeng,HUANG Weidong,LI Jinfei,ZHANG Xudong,SUI Yutang
(Naval Aeronautical and Astronautical University, Shandong Yantai 264001, China)
Abstract:In order to evaluate aging kinetics and disclose aging mechanism of composite solid propellant under cycling temperature loading, the limit that the method to process data in traditional high temperature accelerated aging for cycle temperature accelerated aging was discussed. The aging kinetics model under cycle temperature was built. The method for calculating equivalent temperature and equivalent cycling time and formula for calculating activation energy was given. The aging mechanism of composite solid propellant under cycling temperature condition was proposed. Those methods make life prediction accord with actual storage condiction with better correlation.
Keywords:composite solid propellant; cycling temperature; aging kinetics; equivalent temperature

