基于Convex最优化的室内可见光通信灯排布

周中山，叶蔚萍

(南京邮电大学 通信与信息工程学院，江苏 南京 21003)



基于Convex最优化的室内可见光通信灯排布

周中山，叶蔚萍

(南京邮电大学 通信与信息工程学院，江苏 南京 21003)

摘要：非相干多径弥散信道的特性和LED灯发射机的特性使得室内可见光通信系统难以提供室内均匀的通信性能。为了获得近似均匀的通信性能，提出了一种通过反向设计的基于Convex优化的灯排布方案。仿真结果显示，提出的灯排布方案使系统的接收光功率波动从2.706 dB下降到0.277 dB，Q因子从3.224上升到36.271，并符合照明要求。

关键词：反向设计；Convex最优化；接收光功率波动；Q因子

引用格式：周中山，叶蔚萍. 基于Convex最优化的室内可见光通信灯排布[J].微型机与应用，2016,35(12)：70-72.

0引言

与传统的照明设备相比，发光二极管(LED)具有功耗低、光电转换效率高、使用寿命长等优点，被广泛地认为是下一代绿色照明工具[1-4]。随着LED光源制造技术的不断发展以及市场覆盖率的不断提高，将照明和数据通信相结合的室内可见光通信已经得到越来越多学者的广泛研究。虽然在室内可见光通信的系统研究和设计方面已经有很大的进步[5]，但是由于非相干多径弥散信道特性和LED光发射机特性导致的功率覆盖不平坦仍然是一个严峻的问题。

在相关的基于定量优化的灯排布方案设计中[6]，一种人工智能技术——演进算法(Evolution Algorithm)被用于弥补非相干多径弥散信道特性和LED光发射机特性，提高功率覆盖平坦性。为了进一步提高功率覆盖平坦性，本文运用反向设计的思想将最优化理论中的Convex最优化应用于室内可见光通信系统的设计中。本文首先对室内可见光通信系统进行建模，然后提出Convex优化方案，最后进行性能评估。

1室内可见光通信系统模型

本文选用了一个5 m×5 m×3 m无障碍物的典型模型。天花板分成64块大小相等的正方形，每一块分别命名为S1、S2、…、S64。在每块天花板中心均放置一个LED光发射机，向下垂直于通信平面，其半功率角为70°。假设接收面在距离地面0.85 m的高度，平均分成100块大小相等的正方形，每一块分别命名为R1、R2、…、R100。在每块正方形的中心放置一个PD光接收机，接收机的视场角和物理面积分别为60°和1 cm2，并垂直于天花板，如图1所示。

图1　室内可见光通信典型模型

1.1接收光功率

假设每一个LED光源具有朗伯辐射模型，其发光强度可以表示成：

(1)

单位为坎德拉(cd)。在这里φ是LED光源的发射角，m是朗伯辐射模型的阶数，m=ln(1/2)/ln(cos(φ1/2))。光接收机所接收的可见光信号包括两部分：直射链路(Line Of Sight，LOS)部分和非直射链路(Non-LOS)部分。研究表明[1]，直射链路占总能量的95.16%，一次反射占总能量的3.57%。所以，本文仅考虑直射链路和非直射链路中的一次反射。接收光功率可以表示为[7-9]：

(2)

其中,1≤j≤100。为了衡量功率覆盖的平坦性，引入Q因子，它的定义如下：

(3)

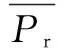
1.2接收光照度

衡量可见光通信系统光照性能的参量是水平光照度E，表达式如下：

(4)

其中，En表示经过n次反射得到的水平光照度。其中直射链路成分E0可以表示成：

(5)

对于高阶(n≥1)分量，其值可以通过下式递归计算[10]：

(6)

其中，ρ表示墙壁的反射系数，φ是LED光源的发射角，φ是光接收机的入射角。根据国际标准化组织的建议，为了满足室内工作需求，光照度需要在300～1 500 lx之间。

2Convex优化方案

2.1Convex最优化的基本概念

一个Convex最优化问题具有如下的形式：

minimizef0(x)

subject tofi(x)≤bi，i=1,…,m

(7)

其中，函数f0，f1，…，fm是凸的，即满足下式：

fi(αx+βy)≤αfi(x)+βfi(y)

(8)

其中,x,y∈Rn或x,y∈R(α+β=1,α≥0，β≥0)。最小均方问题和线性规划问题就是Convex最优化问题的两种。目前，虽然没有通用的解析公式用于解决Convex最优化问题，但是有许多有效的方法可以解决它们，内部点方法是其中比较有效的一种。

2.2目标函数

用一个向量w=[w1，w2，...，w64]来表示每小块中发射机的发射功率。信道矩阵为:

(9)

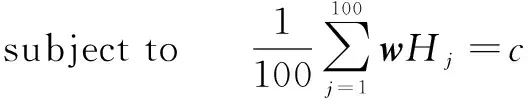
(10)

可以发现上述最优化问题满足Convex最优化问题的判定格式，可用内部点方法来解决这个Convex最优化问题。

在设计之初，c的值并不影响系统平坦性，针对不同的c，只需在设计完成后按比例增大或减小即可。既然相对于灯排布中值的绝对大小，灯排布中各个灯的发射功率之间的比值更加重要，比值一旦确定，功率覆盖平坦性即可确定，所以通过归一化引入系数矩阵的概念。

2.3系数矩阵

对上面部分优化出的w(64)发射功率矩阵进行归一化，得到归一化的发射功率矩阵，并称其为系数矩阵k(64)。系数矩阵一旦确定，功率覆盖平坦性即可确定。对于不同的误码率，对平均接收光功率提出不同的要求时，只需要在系数矩阵的基础上按比例放大或缩小各个LED灯的发射功率。这一性质也显示了本文提出的灯排布方案具有很大的通用性。

3性能评估

通信平面上优化前和优化后的接收功率分布图如图2所示。优化前的接收功率范围为-3.827～1.122 dBm，接收功率波动为2.705 dBm，Q因子为3.224。优化后的接收功率范围为-3.150～-2.873 dBm，接收功率波动为0.277 dBm，Q因子为36.271。对比优化前后的系统，功率覆盖平坦性得到了很大程度的提高。Convex算法迭代的次数为28，算法运行时间复杂度并不是很高。与以前的工作相比[6，10]，功率覆盖平坦性得到了进一步的改善。

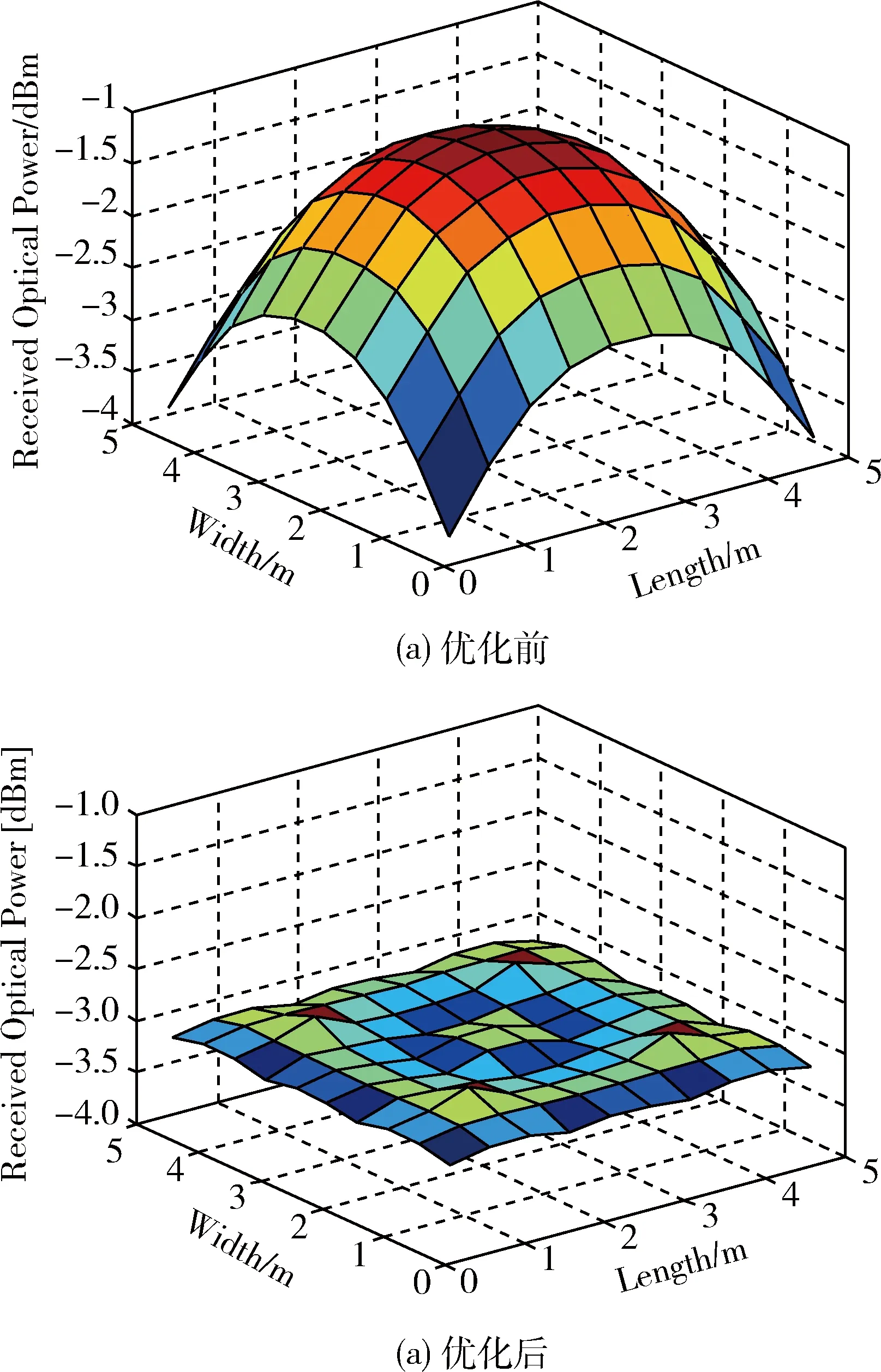
图2　优化前后的接收光功率分布图

优化后的接收光照度分布如图3所示。通过图3可以看到，接收光照度为847～903 lx，系统达到了国际标准化组织建议的办公环境要求。表征设计方案的系数矩阵如图4所示，系数矩阵只有4种颜色(包含表示0的颜色)，意味着在实际的工程安装中只需要4种比例调节器。

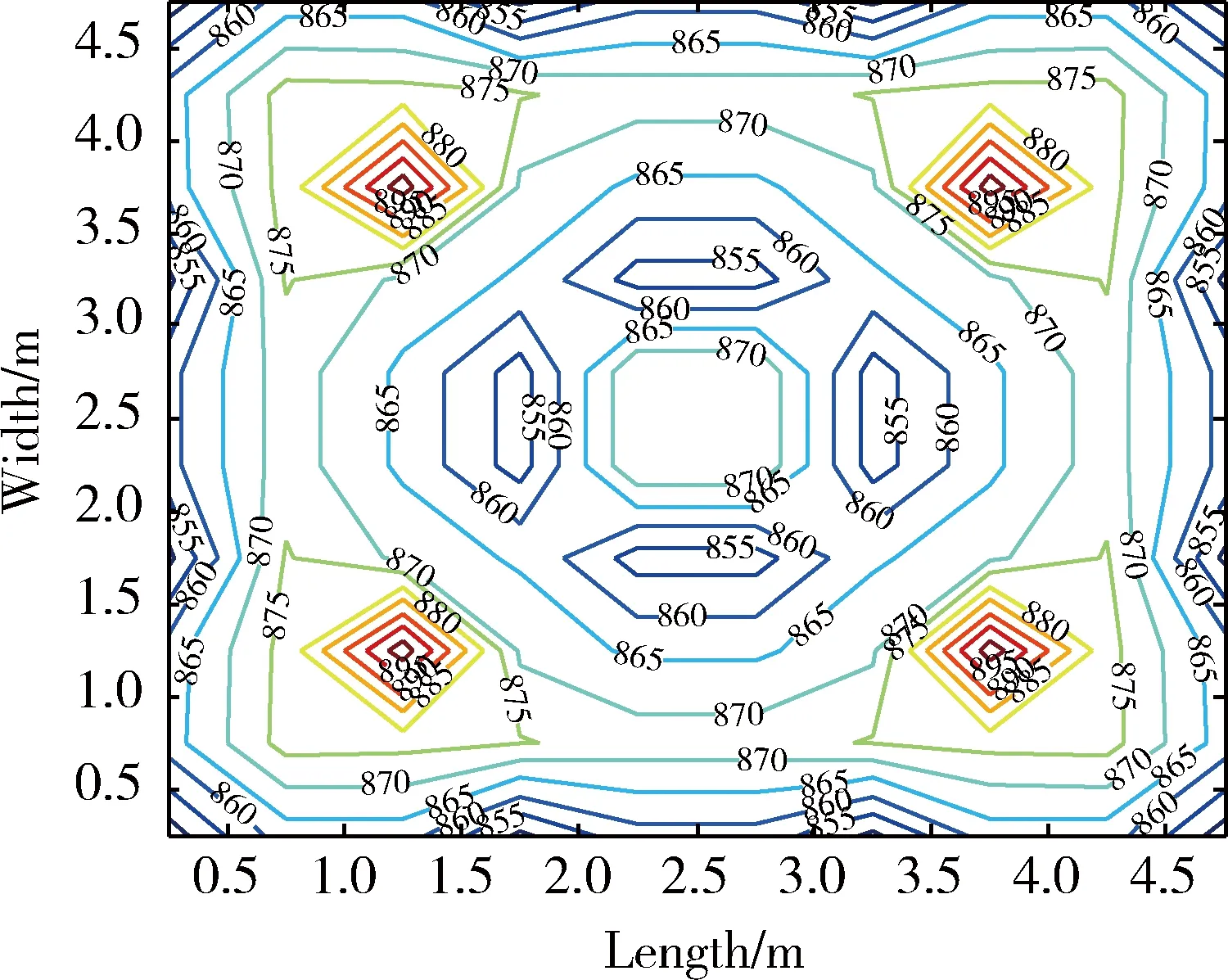
图3　优化后的接收光照度分布

图4　系数矩阵

4结论

本文通过反向设计的思想设计出基于Convex优化的室内可见光灯排布方案。仿真结果显示，在这种方案下，功率覆盖平坦性得到了一定程度的提高，同时，满足办公环境的照明要求。

参考文献

[1] KOMINE T, NAKAGAWA M. Fundamental analysis for visible-light communication system using LED lights[J]. IEEE Transactions on Consumer Electronics, 2004, 50(1): 100-107.

[2] 刘洋,章国安,何黄燕，等.基于高效纠错码的无线光通信系统性能分析[J].电子技术应用,2014,40(12):103-106.

[3] Zeng Lubin, O′BRIEN D C, LE-MINH H, et al. Improvement of date rate by using equalization in an indoor visible light communication system [C]. Proceedings of 4th IEEE International Conference on Circuits and Systems for Communications, ICCSC, 2008, 678-682.

[4] KAHN J M, BARRY J R. Wireless infrared communications[J]. Proceedings of the IEEE, 1997, 85(2): 265-298.

[5] KOMINE T, LEE J H, HARUYAMA S, et al. Adaptive equalization system for visible light wireless communication utilizing multiple white LED lighting equipment[J]. IEEE Transactions on Wireless Communications, 2009, 8(6): 2892-2900.

[6] Ding Jupeng, Huang Zhitong, Ji Yuefeng. Evolutionary algorithm based power coverage optimization for visible light communications[J]. Communications Letters, IEEE, 2012, 16(4): 439-441.

[7] Zeng Lubin, O′BRIEN D C, LE-MINH H, et al. High data rate multiple input multiple output (MIMO) optical wireless communications using white LED lighting[J]. IEEE Journal on Selected Areas in Communications, 2009, 27(9): 1654-1662.

[8] POHL V, JUNGNICKEL V, von HELMOLT C. Integrating-sphere diffuser for wireless infrared communication[J]. IEE Proceedings-Optoelectronics, 2000, 147(4): 281-285..

[9] BARRY J R, KAHN J M, KRAUSE W J, et al. Simulation of multipathimpulse response for indoor wireless optical channels[J]. IEEE Journal on Selected Areas in Communications,1993, 11(3): 367-379.

[10] Wang Zixiong, Yu Changyuan, Zhong Wende, et al. Performance of a novel LED lamp arrangement to reduce SNR fluctuation for multi-user visible light communication systems [J]. Optics Express，2012, 20(4): 4564-4573 .

中图分类号：TN929.1; TN911.74

文献标识码：A

DOI：10.19358/j.issn.1674- 7720.2016.12.022

(收稿日期：2016-01-27)

作者简介：

周中山(1991-)，男，硕士研究生，主要研究方向：室内可见光通信技术。

Convex optimization based LED lamps arrangement for visible light communication

Zhou Zhongshan, Ye Weiping

(College of Telecommunication and Information Engineer, Nanjing University of Posts and Telecommunications, Nanjing 21003, China)

Abstract:The characteristics of inherent multipath diffuse channel and LED optical transmitters make it difficult for visible light communication to provide uniform communication performance. A LED lamp arrangement scheme based on Convex optimization by reverse design is proposed to achieve approximate uniform communication performance. Simulation result shows proposed LED arrangement schema makes the received optical power range from 2.706 dB to 0.277 dB and Q-factor from 2.210 to 29.985, respectively meeting the illuminance need.

Key words:reverse design; Convex optimization; received power fluctuation; Q-factor