双星光学观测体系的目标定位误差分析

杨　虹，张占月，丁文哲，陈　 峰

(1.装备学院 研究生管理大队，北京 101416；2. 装备学院 航天指挥系，北京 101416)



双星光学观测体系的目标定位误差分析

杨虹1，张占月2*，丁文哲1，陈 峰1

(1.装备学院 研究生管理大队，北京 101416；2. 装备学院 航天指挥系，北京 101416)

摘要：为提高双星光学观测体系的定位精度，构建了新型双星光学定位系统。通过对卫星、光电观测平台的建模，构建了地惯系下平台与目标间的观测矢量模型。利用几何定位算法，推导出了地惯系下的目标定位模型与定位误差模型，并利用蒙特卡罗法获得了定位误差分布。在此基础上，引入了小波理论进行误差的优化重构，以提高双星光学观测体系的定位精度。利用测量数据进行仿真，结果表明，引入小波理论对目标定位误差进行降噪重构后，可以使目标定位精度提高30%，为工程上减小目标定位误差提供了新的思路。

关键词:双星光学定位误差；星载光电观测平台；小波分析

1引言

近年来，随着光电探测技术的发展，天基探测方式凭借其不受地域、大气影响的独特优势，逐渐为世界所关注，得到了快速的发展。

相比于利用雷达时差和频差的短距离定位方式，光学定位方式限制约束更少，作用距离更远，更加适合于天基探测[1]。考虑到在被动测角方式下，单星无法通过单次测量对目标进行定位[2]，因此搭建双星光学观测体系，计算定位误差，并对误差进行分析具有十分重要的意义。

美国在此领域的研究要远远快于其他国家。其中“空间目标监视系统” (SBSS)与“空间跟踪与监视系统” (STSS)已经投入了使用[3-6]。国内也在不断开展此项技术的研究。张萍[7]针对地球静止轨道卫星分析了其视线误差。谢凯[8]、盛卫东[9-10]等人针对卫星、相机结构构建了传感器测量模型，分析了天基光学监视系统的目标定位精度。

目前实际应用中的观测方式是将空间相机安装于星载光电观测平台上[11-12]，通过采用多种控制方式对相机视轴进行调控，相比于将相机直接安装在卫星上，可以减少对卫星本体姿态的控制，并降低控制难度。因此，本文针对分别搭载于两颗卫星上的光电观测平台，构建了新型双星光学观测体系目标定位模型。考虑到问题的复杂性，为了保证结果与实际最大程度贴近，建立了基于蒙特卡罗方法的目标定位误差模型。

关于最终定位误差的分析，现有文献大多都是根据各项误差的影响因子，对定位体系进行误差分配，从而降低定位误差[13-15]。本文从另一角度出发，引入小波理论，对定位误差进行优化重构，大幅提高了双星光学观测体系的目标定位精度。为实际应用中节约成本，提高双星光学观测体系的定位精度，提供了新的思路。

2星载光电平台观测矢量模型

2.1定位误差来源

双星光学观测体系中的误差源主要包括：观测系统静态指向误差、动态稳定误差、观测系统与卫星间的对准误差及卫星的测量误差等，如表1所示。

表1　误差源

从表1中可以发现，实际中影响观测系统最终定位精度的误差源种类繁多，分析困难。但总体上却可以将其分为两大类：微观误差和宏观误差。微观误差作为最根本的误差来源，影响了宏观误差的大小。本文不研究微观上的各种误差问题，只从宏观层面对观测系统的成像过程进行考虑，分析双星光学观测体系的目标定位误差。

2.2工作过程及单星成像模型

双星光学观测系统由两颗观测卫星组成，每颗卫星上都载有两轴两框架式光电观测平台，通过求得每颗卫星在空间中的位置以及卫星与目标间连线的视线矢量，从而获取目标的空间位置信息。定位过程如图1所示。

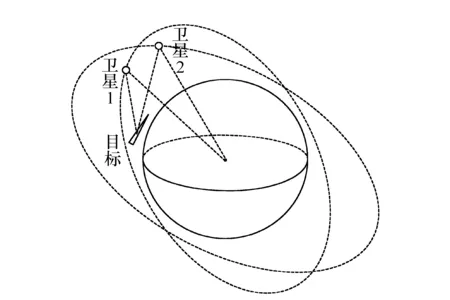
图1　双星定位示意图 Fig.1　Schematic of double satellites positioning

双星光学观测体系中的每颗卫星通过相关姿态敏感器得到自身的姿态角信息，以及星上光电平台内、外框架的转动角信息，再通过空间相机测量得到目标的成像位置信息，从而获得卫星与目标间的观测矢量。整个测量过程如图2、3、4所示。

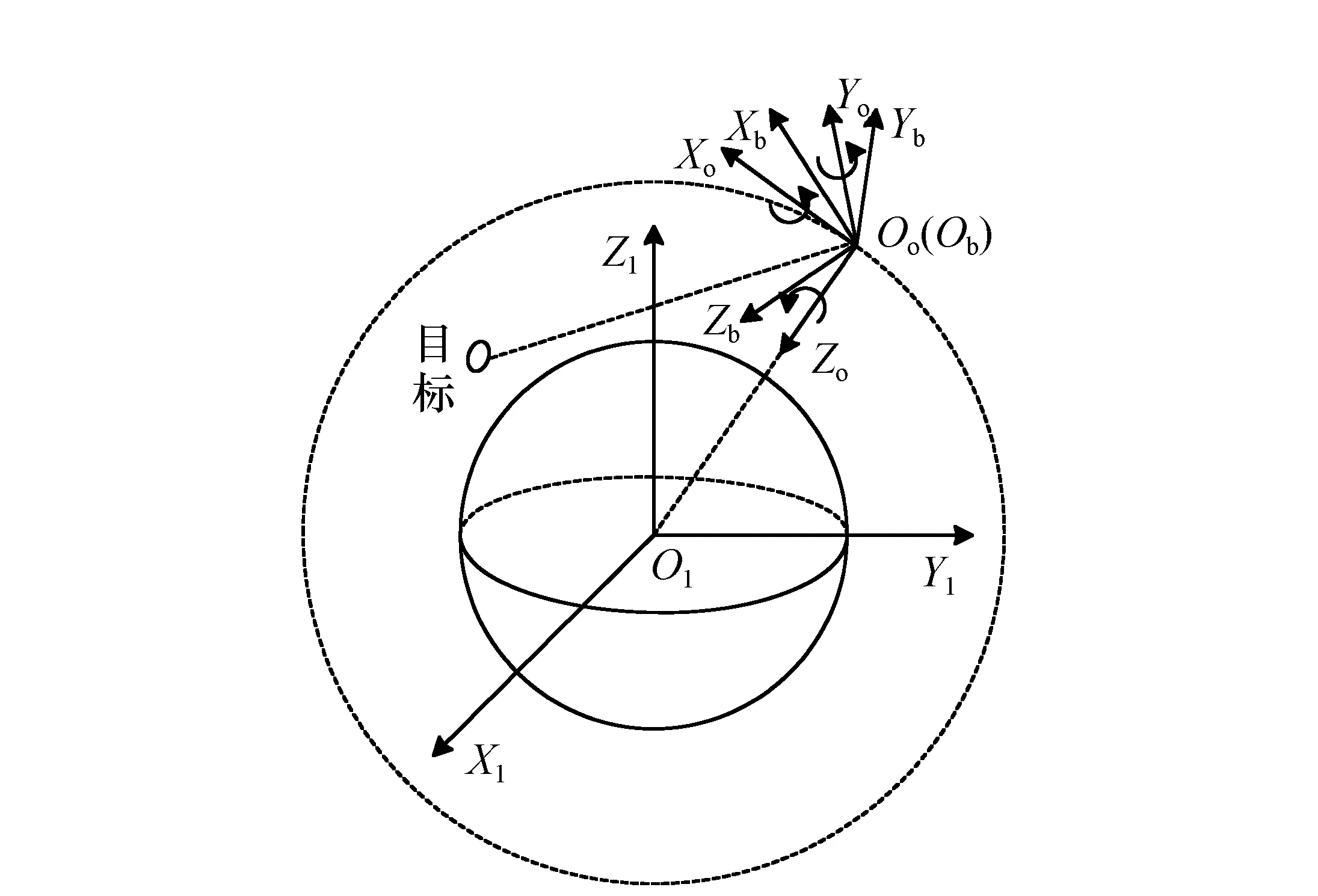
图2　单星观测示意图 Fig.2　Schematic of single satellite observation

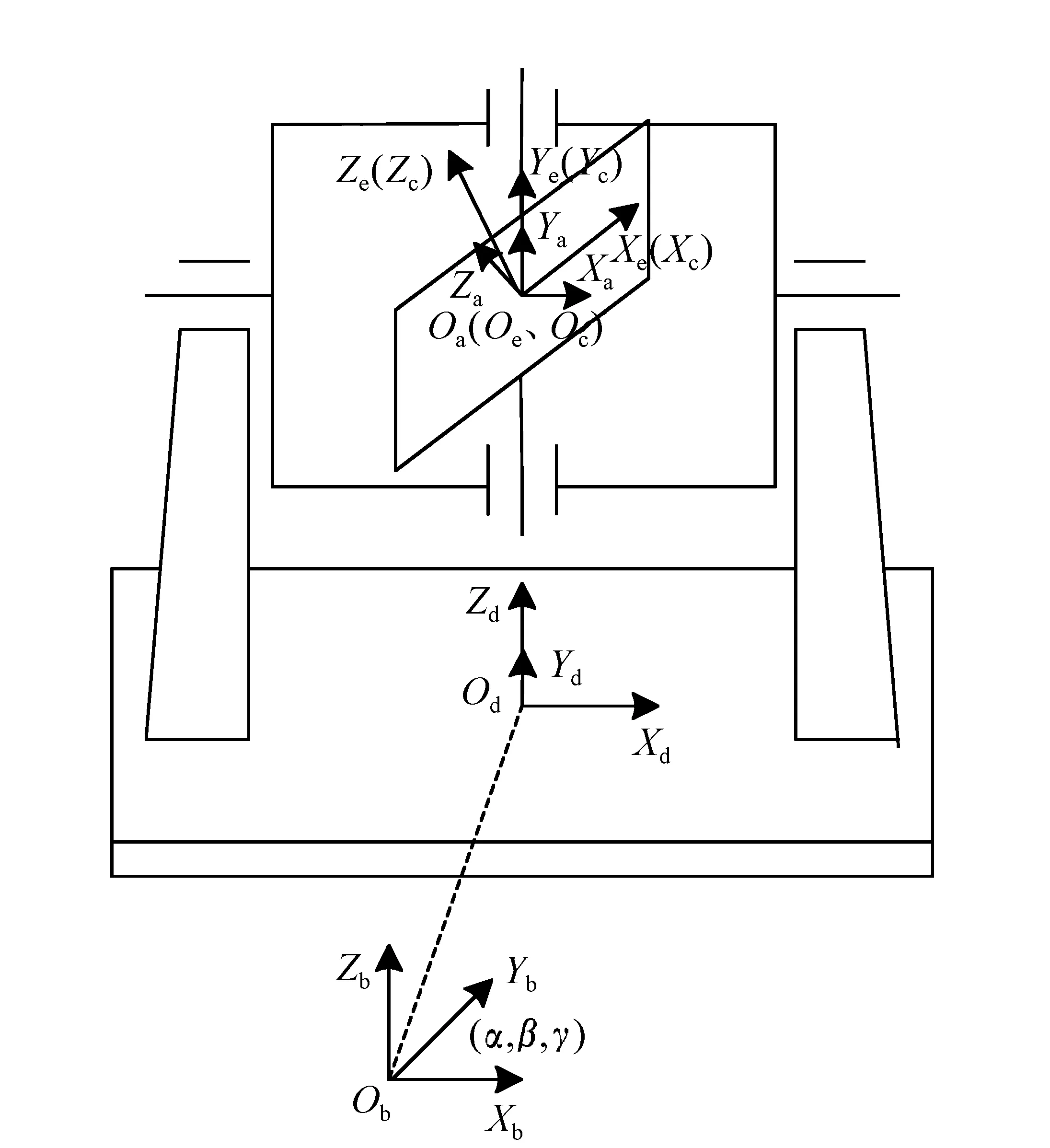
图3　星载光电平台结构 Fig.3　Schematic of space borne optical platform

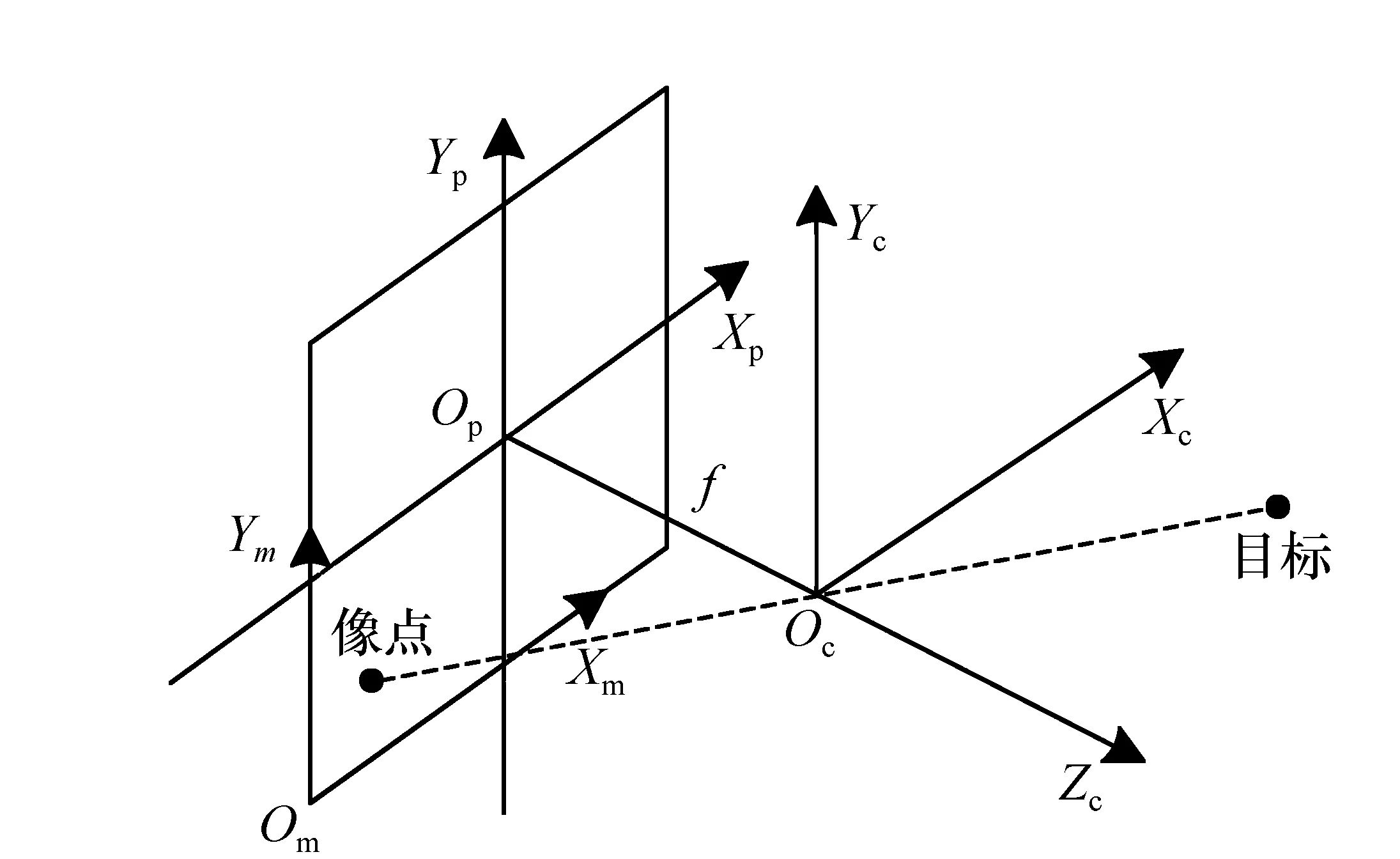
图4　透视过程 Fig.4　Schematic of perspective process

从图2～4可以看出，在整个单星成像过程中共经过了9次坐标系的转换，依次是：地心惯性坐标系{OlXlYlZl}、卫星轨道坐标系{OoXoYoZo}、星体坐标系{ObXbYbZb}、光电平台坐标系{OdXdYdZd}、外框架坐标系{OaXaYaZa}、内框架坐标系{OeXeYeZe}、传感器坐标系{OcXcYcZc}、图像物理平面坐标系{OpXpYp}、图像像素平面坐标系{OmXmYm}。具体的成像过程如图5所示。

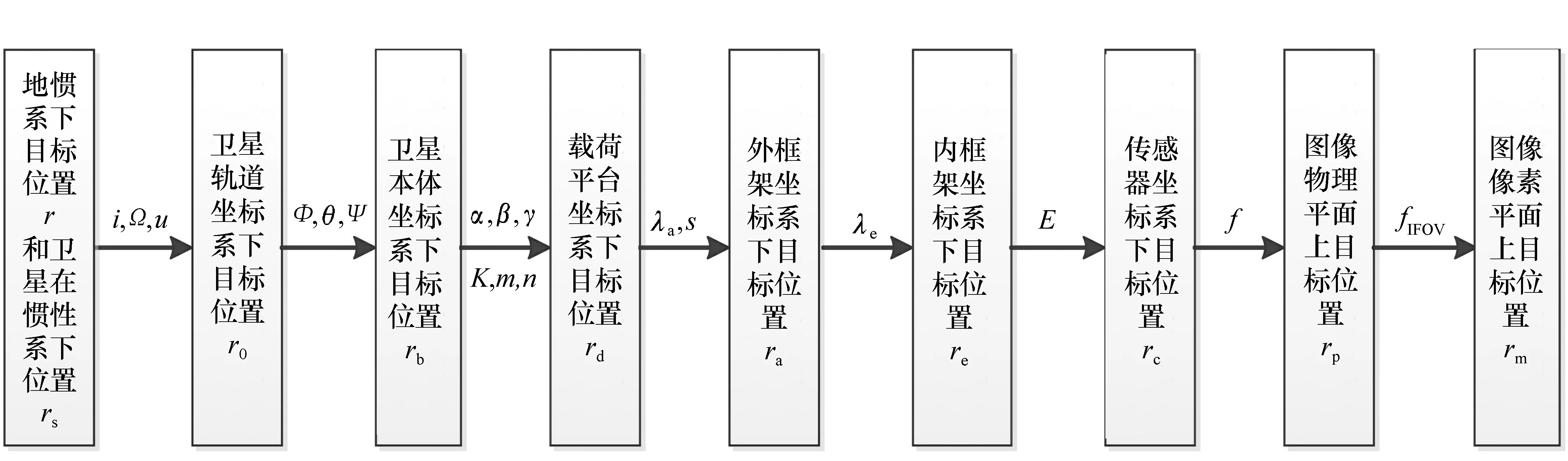
图5　单星观测成像过程 Fig.5　Imaging process of single satellite observation

图5中各参量的定义分别为：轨道参数(i,Ω,u)为坐标系OlXlYlZl到OoXoYoZo的轴转动角、姿态参数(φ,θ,ψ)为坐标系OoXoYoZo到ObXbYbZb的轴转动角、卫星光电观测平台的安装角(α,β,γ)与安装位置(k,m,n)分别为坐标系ObXbYbZb到OdXdYdZd的轴转动角与原点平移量，光电观测平台上内、外框架转动角λa与λe为坐标系OdXdYdZd、OaXaYaZa、OeXeYeZe间的轴转动角，外框架原点位置s为坐标系OdXdYdZd到OaXaYaZa的原点平移量，单位矩阵E表示坐标系OeXeYeZe与OcXcYcZc重合，焦距f表示坐标系OcXcYcZc中心到OpXpYp的距离，瞬时视场角fIFOV表示相机探测单元对应的瞬时视场。

目标从坐标系OlXlYlZl到OcXcYcZc的映射过程如下:

(1)

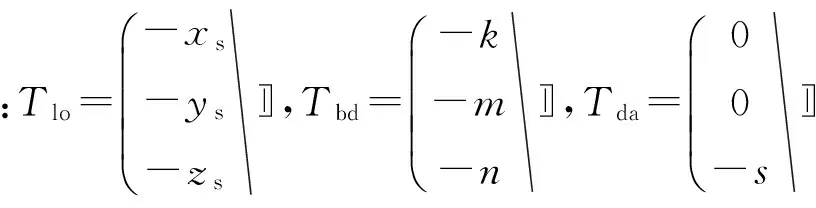
目标从坐标系OcXcYcZc到OmXmYm的映射过程如下：

(2)

(3)

(4)

式中：[·]表示取整，h(·)表示式(4)的量化函数。

2.3观测矢量模型

本文将观测矢量定义为卫星光电平台上的观测相机与空间目标在地心惯性坐标系下的单位连线矢量。由于星内各装置的安装平移量均处于米级范围，而卫星与观测目标间的距离处于百公里范围，在对成像模型进行单位化时，可以发现对于观测矢量来说，旋转量的误差影响占主要因素，而平移量的影响则可以忽略不计。

将式(1)两边同时除以|r-rs|得：

(5)

式中，vc为卫星光电平台上观测相机与空间目标在传感器坐标系下的单位连线矢量，v为卫星的观测矢量。

对式(5)取逆过程得到星载光电平台观测矢量模型为：

(6)

式中，h-1(rm)为:

(7)

3双星光学观测体系目标定位模型

3.1卫星轨道

双星光学观测体系对空间目标进行定位时，需要双星在地惯系下的位置信息。根据天体学运动规律，可以方便地由卫星的轨道根数得到卫星在地惯系下的空间位置rsi(i-1,2):

Ei=Mi+eisin(Ei)

(8)

(9)

Pi=

(10)

(11)

(12)

式中，下标i表示卫星编号，Ei为偏近地点角，Mi为平近地点角，ni为平均角速度，μ为开普勒常数，ei为偏心率，ωi为近地点幅角。

3.2目标定位模型

参考文献由[16]可知，目前常用的无源定位

算法有3种，依次是几何定位算法、基于奇异值分解的最小二乘算法、总体最小二乘算法。对于本文的双星光学观测体系来说，几何定位算法不仅可以得到理论上的最优解，并且计算速度最快，定位精度最高。故本文采用几何定位算法得出目标的定位模型。

在实际观测过程中，由于误差的存在，观测系统中两颗卫星的观测视线可能存在一定偏差，导致两条观测视线在空间中并不能交于一点。这时，可以采用两条视线的公垂线中点作为目标的实际空间位置，使得定位误差最小。

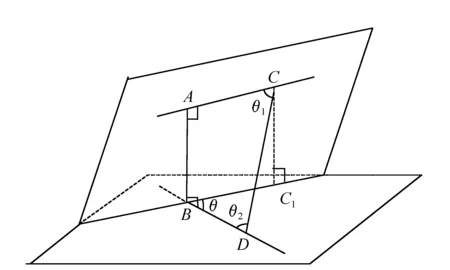
图6　目标定位 Fig.6　Schematic of target location

定位过程如图6所示。图中的C与D分别表示两颗观测卫星在地惯系下的空间位置rs1、rs2，CA与DB分别表示两颗卫星的观测视线，其单位矢量即为观测矢量v1、v2，AB为两视线的公垂线。

设C(x1,y1,z1)、D(x2,y2,z2)，v1(a1,b1,c1)、v2(a2,b2,c2)，可得：

(13)

(14)

(15)

根据空间异面直线定理得：

(16)

(17)

则空间目标在地惯系下的位置为：

(18)

4双星光学观测体系的定位误差分析

4.1基于蒙特卡罗方法的定位误差模型

对于目标定位误差分布的求取，主要有两种方式：基于全微分和最小二乘法的误差分布求取[10]与基于蒙特卡罗方法的误差分布求取[17]。前者计算简单便捷，快速直观，但公式推导困难，且推导过程中假设条件与最小二乘算法所导致的误差可能使最终结果过于乐观。后者虽然仿真复杂，计算量大，但统计结果更加可信。综合考虑，本文选用蒙特卡罗方法得到最终的误差分布。

蒙特卡罗方法(Monte Carlo)是基于大数定律的一门理论，通过构造概率产生过程，并从中进行抽样，得到大量的随机数，使仿真无限贴近于实际，得到相对来说较好的结果[17]。

基于蒙特卡罗方法建立的目标定位误差模型为：

(19)

式中：Δx、Δy、Δz表示定位误差；ΔX表示参数误差。

具体步骤如下：

步骤1：将测量所得的双星光学观测体系运行数据，代入前文所推导的目标定位模型中，计算出目标在地惯系下的理想空间位置。

步骤2：利用蒙特卡罗方法分别产生与双星系统中各误差分布情况相同的随机样本。

步骤3：将产生的随机样本作为噪声添加到各个测量值上，代入各模型中，得到目标在地惯系下的实际空间分布。

步骤4：利用定位误差模型式(19)得到双星观测体系的目标定位误差分布。

4.2测量参数及蒙特卡罗仿真实验

仿真中的误差数据是根据各项误差的分布特性，基于各自坐标系下，由蒙特卡罗方法产生。各项误差特性则是参照文献[8-10]给定。在实际过程中各项误差的具体取值，则需要根据特定任务系统，通过分析各项微观误差源得到。

文献[18]给出了双星光学观测体系在对目标观测过程中的系统运行数据，如表2所示。

表2　双星光学观测体系参数

双星观测误差由双星各自产生，但由于双星采用的系统相同，所以给定双星各自的误差符合同样规律。本次仿真实验取Monte Carlo仿真次数为10 000，双星位置误差Δrsi均符合高斯分布，大小均为100 m，RΔrsi=diag[1002,1002,1002]；双星轨道误差(Δii, ΔΩi, Δui)均符合高斯分布，大小均为20 μrad；双星姿态误差(Δφi,Δθi,Δψi)均符合高。斯分布，大小均为25 μrad；双星光电平台振动误差(Δαi,Δβi,Δγi)均符合均匀分布，大小均为30 μrad；双星光电观测平台内、外框架转动误差(Δλai,Δλei)均符合高斯分布，大小均为10 μrad；双星像素平面脱靶量偏移误差(Δxmi,Δymi)均符合均匀分布，大小均为0.5 pixel。得到目标定位误差在地惯系下分布情况，如图7所示。

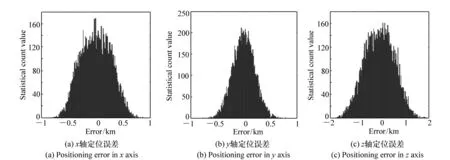
图7　地惯系下目标定位误差分布 Fig.7　Error distribution of target location in the ECI

仿真得到目标在地惯系下的理想空间位置为r(-2.349 km,-58.754 km,-158.758 km)。双星光学观测体系的目标定位误差结果如表3所示。

表3　定位误差分布

4.3小波分析

在双星光学观测系统工作之前，会对系统进行软硬件标定校准，但这并不会使系统工作时的各项误差消失，而只能使系统内的各项误差保持在合理范围内，这就使最终的定位结果具有波动性，定位误差符合某种分布特性。为了提高定位精度，本文引入小波理论对最终定位误差进行优化重构。

小波分析是在傅里叶变换的基础上发展而来的一门新兴理论，它的时—频窗在高、低频时会自动调节窗口大小，具有自适应性，又被成为“数学显微镜”。在分析、处理信号的问题上，被广泛应用，并取得了很好的效果[19]。

接下来利用小波理论对之前仿真得到的目标定位误差进行分解—降噪—重构。

小波基的选取十分关键，理想的小波基应该具有正交性、紧致性、衰减性、对称性、正则性与消失矩。同时分解层数的选取也十分重要，层数选取较少不利于信噪分离，选取过多则失真严重，在工程上一般选取3～5。本文基于以上考虑，选取Symlet(sym3)小波，对原始误差信号进行3层小波分解。Symlet小波是对db小波的改进，在保留db小波较好的各项特性基础上，提升了对称性，可以在一定程度上减少信号的失真。Sym3小波的支撑范围为5，消失矩为3，具备较好的正则性。

由于分析方式近似，下面以x轴定位误差为例进行分析：

(1)对x轴定位误差进行3层小波分解，如图8所示。

原始误差信号s被分解为低频分量a3与高频分量dn(n=1～5)：s=a3+d3+d2+d1。

(2)对各层信号分量进行统计，结果如图9所示。

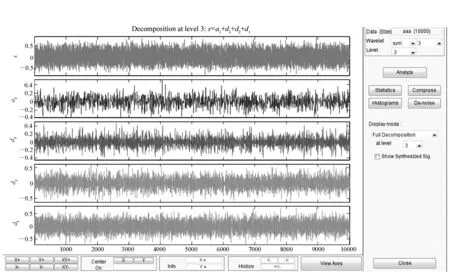
图8　误差分解 Fig.8　Error decomposition

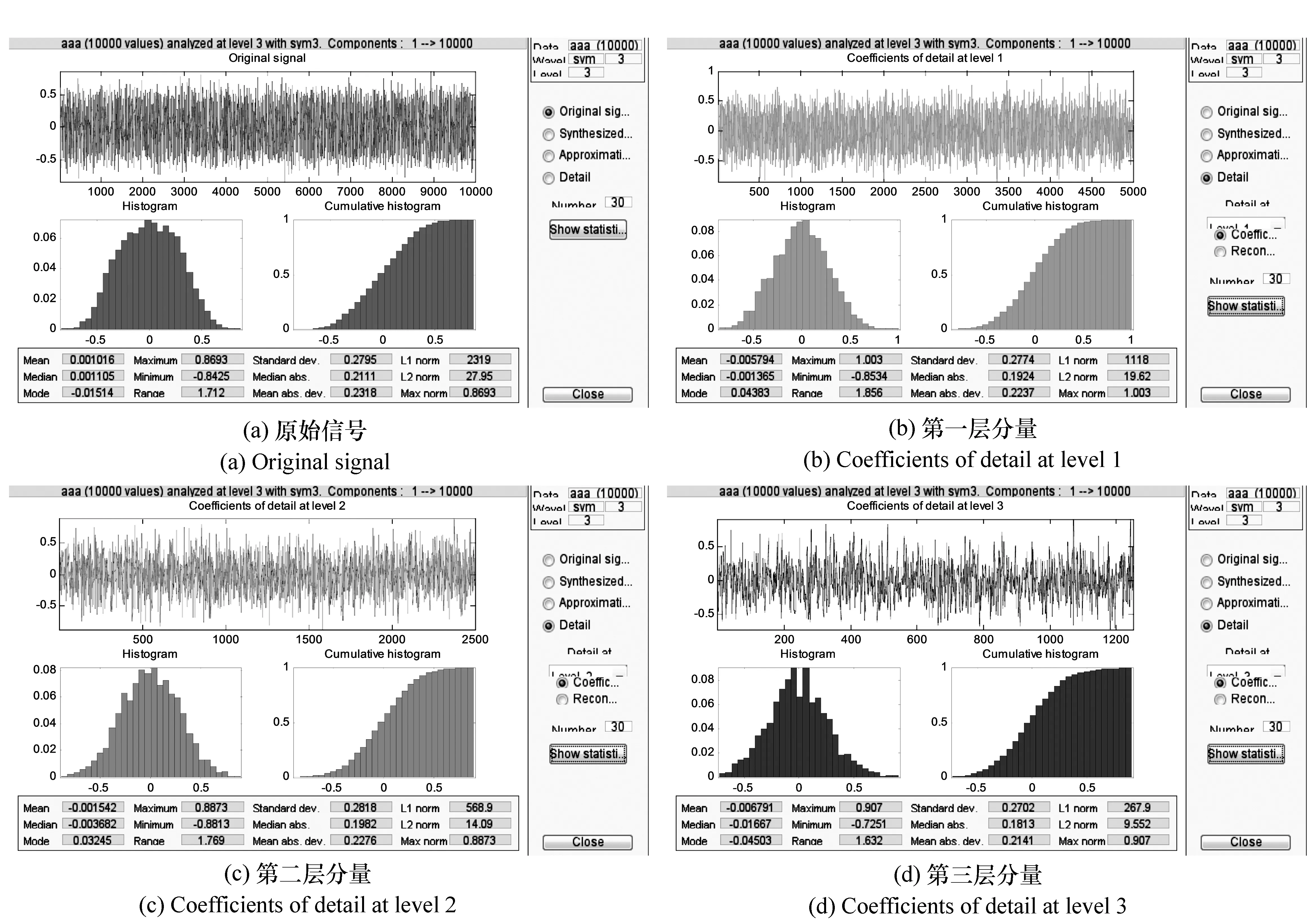
图9　各层信号统计图 Fig.9　Layers of signal statistics

分量均值μ/km均方差δ/kms1.016×10-30.2795d1-5.794×10-30.2774d2-1.542×10-30.2818d3-6.791×10-30.2702

从图9中可以得出，各层分量的统计数据如表4所示。

(3)对原始误差信号进行降噪重构，如图10所示。

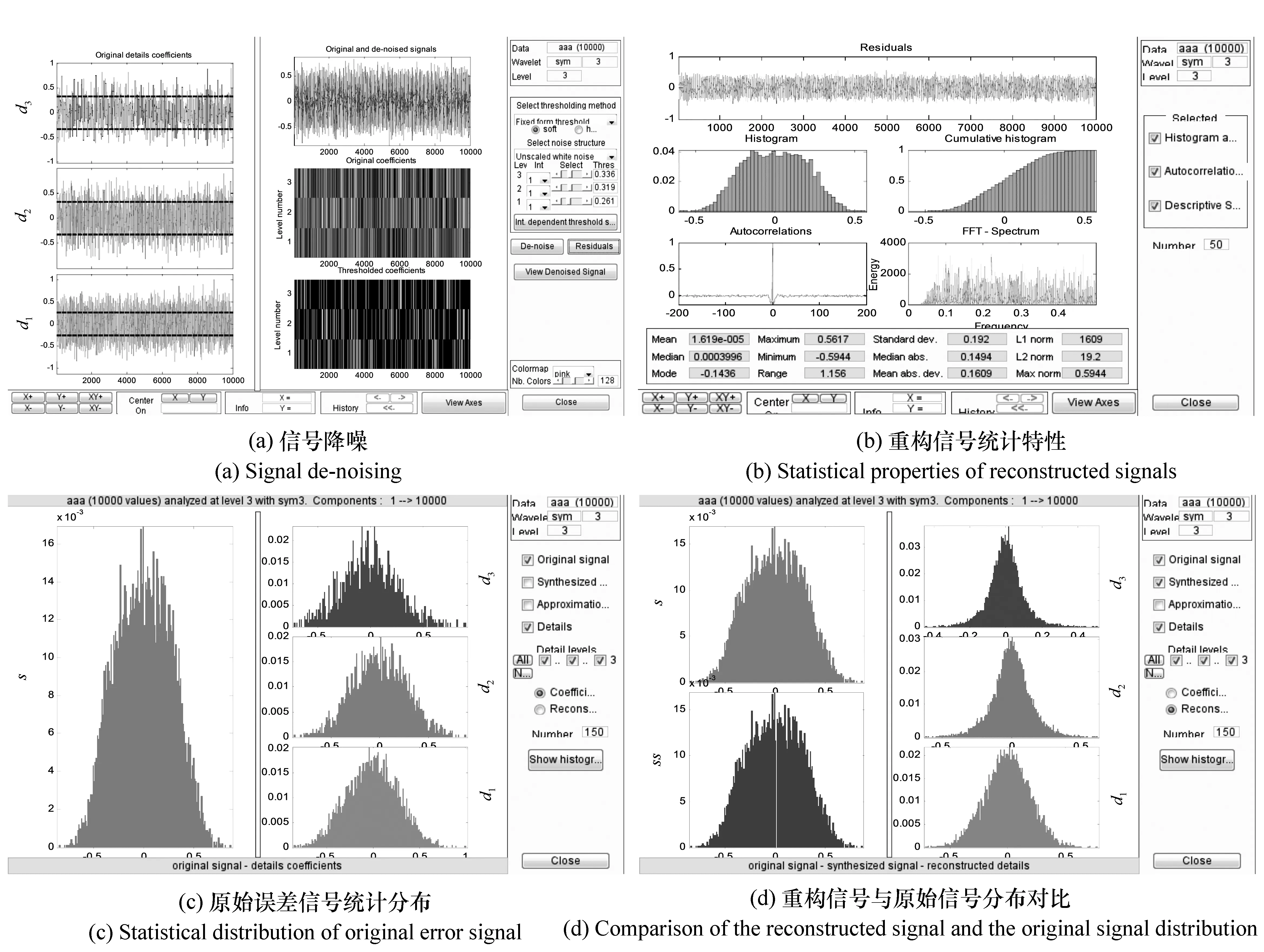
图10　误差信号降噪重构图 Fig.10　Noise reduction and reconstruction of the error signal

从图10可以看出，利用小波分析对原始误差信号进行降噪处理后，得到的重构误差信号相比于原始误差信号，均方差得到了显著的降低，各层重构分量的统计数据如表5所示。

表5　重构信号统计

将表5与表4进行对比，可以看出原始误差信号的均值为1.016×10-3km，均方差为0.279 5 km，而通过小波分析降噪重构之后得到的新误差信号均值为1.619×10-5km，均方差为0.192 km，x轴方向的定位误差Δx从0.279 5 km提高到了0.192 km，定位精度提升了31.3%。

下面分别对y轴方向的定位误差Δy及z轴方向的定位误差Δz进行小波分析，得到重构后的误差分布，如表6所示。

从表6可以看出，引入小波理论后，定位精度得到了较大的提高。y轴原始误差信号的均值为3.276×10-4km，均方差为0.208 km，而通过小波分析降噪重构之后得到的新误差信号均值为-1.192×10-5km，均方差为0.145 km，y轴方向的定位误差Δy从0.208 km提高到了0.145 km，定位精度提升了30.3%。z轴原始误差信号的均值为-3.615×10-4km，均方差为0.595 km，而通过小波分析降噪重构之后得到的新误差信号均值为5.491×10-5km，均方差为0.410 1 km，z轴方向的定位误差Δz从0.595 km提高到了0.410 1 km，定位精度提升了31.1%。

表6　误差前后分布对比

5结论

(1)本文以提高天基无源定位精度为背景，构建了一种新型的双星光学定位体系。首先，根据新型单星观测模式，建立了基于卫星、光电平台的单星观测矢量模型，利用几何定位原理，推导出了双星光学观测体系目标定位模型，根据测量数据，计算出了目标在地惯系下位置。

(2)基于蒙特卡罗方法构建了目标定位误差模型，通过仿真计算发现新型双星光学观测体系的目标定位精度在百米量级，证明了双星光学定位具有一定的可行性。同时得出卫星的位置误差、轨道误差、姿态误差、光电平台振动误差、内外框架转角误差、脱靶量误差是影响双星光学观测体系目标定位的主要因素，为下一步双星光学观测体系的误差分配奠定了基础。

(3)引入了小波理论对目标定位误差进行了降噪重构，仿真计算表明通过进行小波分析，可以使目标的定位精度提高30%以上。该方法为工程上节约成本，减小目标定位误差提供了新的思路。

[1]杨琴,宋锐,马燕新,等.天基空间目标成像仿真系统设计与实现[J].激光与光电子学进展,2015,11:115-123.

YANG Q,SONG R,MA Y X，etal.. Design and implement of space-based target imaging simulation system[J].Laser&OptoelectronicsProgress,2015,11:115-123.(in Chinese)

[2]BLACKMAN S,POPOLI R.DesignandAnalysisofModernTrackingSystems[M]. Norwood,M A:Artech House,1999:700-735.

[3]Space Based Space Surveillance(SBSS)[EB/OL].[2010-09-26].http://www.globalsecurity.org/space/systems/sbss.htm.

[4]TANG Y,ZHONG W N,LI SH. An improved double r-iteration IOD method for GEO UCTs based on SBSS system[J].ChineseJ.SpaceScience,2014,34(6):867-871.

[5]STAIR A T,MILL J D. The Midcourse Space Experiment(MSX)[C]. Proceedings of the 1997 IEEE Aerospace Conference,Snowmass,CO:IEEE,1997:233-245.

[6]VANDENBERG AFB C. STSS Demo Satellites Track Two-Stage Interceptor in Missile Defense Test[EB/OL].[2010-07-08].http://www.asdnews.com/news.

[7]张萍,易东云,吴翊,等.空间预警系统的视线测量误差特性研究[J].中国空间科学技术,2004,6:51-56.

ZHANG P,YI D Y,WU Y,etal.. The LOS measurement error modeling of space early warning system[J].ChineseSpaceScienceandTechnology,2004,6:51-56.(in Chinese)

[8]谢恺,韩裕生,薛模根,等.低轨红外预警星座无源定位精度分析[J].信号处理,2008,3:343-348.

XIE K,HAN Y SH,XUE M G,etal.. Analysis of passive location accuracy in LEO infrared early warning constellation[J].SignalProcessing,2008,3:343-348.(in Chinese)

[9]盛卫东,徐洋,周一宇,等.天基光学传感器的视线测量误差分析[J].宇航学报,2011,1:129-135.

SHENG W D，XU Y，ZHOU Y Y,etal.. Analysis of LOS measurement error for space-based optical sensor[J].J.Astronautics,2011,1:129-135.(in Chinese)

[10]盛卫东,龙云利,周一宇.天基光学传感器网络目标定位精度分析[J].光学学报,2011,31(2):0228001.

SHENG W D,LONG Y L,ZHOU Y Y. Analysis of target location accuracy in space-based optical-sensor network[J].ActaOpticaSinica,2011,31(2):0228001.(in Chinese)

[11]王秀红,李俊峰,王彦荣.天基照相监测空间目标定轨方法及精度分析[J].光学 精密工程,2013,21(6):1394-1403.

WANG X H,LI J F,WANG Y R. Orbit determination and precision analysis of space object with space-based camera[J].Opt.PrecisionEng.,2013,21(6):1394-1403.(in Chinese)

[12]王卫兵,王锐,姜振华,等.天基监视中的双星相对运动模型研究[J].红外与激光工程,2015,44(12):3782-3787.

WANG W B,WANG R,JIANG ZH H,etal.. Research on relative movement model of two satellites in space-based surveillance[J].InfraredandLaserEngineering,2015,44(12):3782-3787.(in Chinese)

[13]ESA Engineering Standardization Board. Pointing Error Engineering Handbook ESSB-HB-E-003[S]. ESA-ESTEC Requirements & Standards Division,2011.

[14]OTT T,BENOIT A,VAN DEN BRAEMBUSSCHE P,etal.. ESA pointing error engineering handbook[C]. 8th International ESA Conference on Guidance,Navigation and Control Systems,Karlovy Vary,Czech,2011.

[15]EISENBIES S K,HOCKEN R J. Error budget by constraints[D]. Charlotte:University of North Carolina at Charlotte,2001.

[16]李罗钢.临近空间飞行器定位跟踪及拦截弹制导问题研究[D]. 哈尔滨:哈尔滨工业大学,2013.

LI L G. Research on the location and of near space aircraft and the guidance of intercepter[D]. Harbin:Harbin Institute of Technology,2013.(in Chinese)

[17]周晓尧,范大鹏,张智永.升降式光电探测平台定位原理与误差分析[J].宇航学报,2011,32(6):1416-1422.

ZHOU X Y,FAN D P,ZHANG ZH Y. Positioning principle and error analysis for lift electro optical detection platform[J].J.Astronautics,2011,32(6):1416-1422.(in Chinese)

[18]王卫兵,王挺峰,郭劲.基于双星双目跟踪方式的空间目标定轨技术研究[J].光学学报,2015,35(1):0112006.

WANG W B,WANG T F,GUO J. Research on orbit determination technology for space target based on method of tracking with double satellites and double cameras[J].ActaOpticaSinica,2015,35(1):0112006.

[19]刘卫，王荣兰，刘四清，等.基于小波变换的卫星阻力系数分析[J].宇航学报,2015,36(2):142-150.

LIU W,WANG R L,LIU S Q,etal.. Analysis of satellite drag coefficient based on wavelet transformation[J].J.Astronautics,2015,36(2):142-150.(in Chinese)

收稿日期:2016-04-06；

修订日期:2016-04-26

基金项目：部委资助项目

文章编号2095-1531(2016)04-0452-11

中图分类号：V443.5

文献标识码:A

doi:10.3788/CO.20160904.0452

作者简介：

杨　虹(1991—)，女，四川绵竹人，硕士研究生，主要从事航天任务分析与设计方面的研究。E-mail:1558513572@qq.com

张占月(1973—)，男，河北吴桥人，博士，教授，博士生导师，主要从事航天系统仿真方面的研究。E-mail:zhangzhan-yue@163.com

Position error analysis of double satellites optical observation system

YANG Hong1, ZHANG Zhan-yue2*, DING Wen-zhe1, CHEN Feng1

(1.DepartmentofGraduateManagement,EquipmentAcademy,Beijing101416,China;2.DepartmentofSpaceCommand,EquipmentAcademy,Beijing101416,China)*Correspondingauthor,E-mail:zhangzhan-yue@163.com

Abstract:In order to improve the positioning accuracy of double satellites optical observation system, a new type of optical positioning system is constructed. Based on the modeling of the satellite and the optical observation platform, the observation vector model between the platform and the target is constructed. According to the geometric location algorithm, the target location model and the location error model are derived, and the location error distribution is obtained by the Monte Carlo method. On this basis, wavelet theory is brought to optimize and reconstruct error for improving the positioning accuracy of double satellites optical observation system. Using the measured data for simulation, the results show that the wavelet theory introduced to reconstruct the position error can make the positioning accuracy increase by 30%. It provides a new way to reduce the location error in engineering.

Key words:position error of double satellites optical observation system;space-borne optical observation platform;wavelet analysis