基于非负矩阵分解的大规模异构数据联合聚类

申国伟 杨 武 王 巍 于 淼 董国忠

（哈尔滨工程大学信息安全研究中心 哈尔滨 150001）（shenguowei＠hrbeu．edu．cn）

基于非负矩阵分解的大规模异构数据联合聚类

申国伟 杨 武 王 巍 于 淼 董国忠

（哈尔滨工程大学信息安全研究中心 哈尔滨 150001）（shenguowei＠hrbeu．edu．cn）

异构信息网络中包含多类实体和关系．随着数据规模增大时，不同类实体规模增长不平衡，异构关系数据也变得异常稀疏，导致聚类算法的时间复杂度高、准确率低．针对上述问题，提出了一种基于关联矩阵分解的2阶段联合聚类算法FNMTF－CM．第1阶段，抽取规模较小的一类实体中的关联关系构建关联矩阵，通过对称非负矩阵分解得到划分指示矩阵．与原始关系矩阵相比，关联矩阵的稠密度更高，规模更小．第2阶段，将划分指示矩阵作为关系矩阵三分解的输入，进而快速求解另一类实体的划分指示矩阵．在标准测试数据集和异构关系数据集上的实验表明，算法准确率和性能整体优于传统的基于非负矩阵分解的联合聚类算法．

随着微博、社交网络等异构信息网络的兴起，异构信息挖掘已经成为当前数据挖掘领域中的一个研究热点．异构网络中包含多类实体，实体之间存在着复杂的交互关系．例如微博中包含用户、消息、标签、词等实体，用户发布消息，消息由词语组成，消息中还包含标签等．通过抽取实体间的关系数据进行聚类分析，能够挖掘出异构网络中不同实体间的潜在结构关系．

联合聚类能够针对不同的实体同时进行聚类分析［12］，因而应用广泛．传统的联合聚类算法包括基于信息理论的算法ITCC［3］、基于矩阵谱信息［4］和矩阵分解的方法．由于关系数据中一般都是非负元素，非负矩阵分解方法［5］成为目前最常用的方法．

传统的非负矩阵分解仅仅处理同类节点之间的同质关系聚类问题，Long等人［6］首次在二元关系矩阵上运用块值分解法实现矩阵分解．在此基础上，提出了一系列改进的非负矩阵分解方法实现联合聚类［7－9］．采用半监督的非负矩阵分解方法实现联合聚类［1012］，算法SS－NMF［12］中融合肯定链接或否定链接等约束信息提高联合聚类算法的准确度，但是真实数据中通常很难获取约束先验知识．

在处理关系数据时，Wang等人［13］提出了快速的非负矩阵三分解方法FNMTF实现快速的矩阵分解，进而实现联合聚类．非负矩阵分解在联合聚类算法取得了很好的效果［14］，但是数据本身的几何结构会影响聚类的准确性［15－16］．当待分析的异构数据规模增大时，关系数据结构呈现明显变化．主要存在以下问题：

1）非平衡问题．待分析的异构数据规模增大时，异构数据中不同类实体的规模并不呈现统一的增长模式．例如微博消息数量呈线性增长时，用户、词和标签等实体并不呈现线性增长模式．传统的非负矩阵分解方法的时间复杂度都与矩阵的行和列规模相关，因此处理大规模异构数据时计算时间复杂度较高．

2）稀疏性问题．真实异构网络中的关系数据比较稀疏，随着待分析异构数据规模进一步增大，关系数据变得异常稀疏．例如微博中的消息内容最多包含140个字，构建的消息和词之间的关系矩阵非常稀疏．当消息规模进一步增大时，由于中文常用词的数量是一定的，因此消息和词之间的关系矩阵变得异常稀疏，消息和用户、标签的关系矩阵同样如此．传统的非负矩阵分解方法针对异常稀疏的关系矩阵进行分解时得到的聚类效果并不理想．

本文针对大规模异构数据分析时出现的非平衡和稀疏性2个问题进行解决．针对非平衡增长问题，在非负矩阵分解时提出了2阶段分解方法．首先，仅对关系矩阵中的规模较小的一类实体进行分析．异构实体之间的关系矩阵非常稀疏，但是同一类实体之间的关联性比较强［17］，通过同类实体之间的关联关系构造的关联矩阵能够明显提高矩阵的稠密度．其次，以较小规模的实体聚类结果直接作为第2阶段的输入，在确保大规模实体聚类结果的同时提高了整体处理效率．

综上所述，本文将针对大规模异构关系数据提出一种基于关联矩阵的2阶段快速联合聚类算法，同时解决非平衡问题和稀疏性问题．

1 问题定义

异构关系数据中包括多类实体，目前的联合聚类算法主要针对二阶异构关系进行联合聚类分析，因此，本文以2类实体之间的异构关系为例叙述．二阶异质关系数据采用二部图G＝（V，E，W）进行建模，其中V＝X1∪X2，X1和X2为异构关系中的2类实体，实体X1和X2的数量分别为m和n，E为异构关系对应的边集合，W为边的权重．进一步可将二部图G表示成m×n的异构关系矩阵R，由于大规模数据中的非平衡问题，可假设mn．

传统的联合聚类算法中将X1和X2分别划分到k1和k2类（通常k1＝k2），本文将针对X1和X2的联合聚类问题转换成针对关系矩阵R的行和列同时进行划分的问题．

2 2阶段非负矩阵分解框架

针对大规模异构关系数据中的非平衡问题和稀疏性问题，本文提出了一个2阶段的非负矩阵分解框架，如图1所示．

对关系矩阵R的行和列同时聚类可将关系矩阵R分解为F，S，B三个矩阵，如图1（a）所示，其中矩阵F，B分别为2类目标实体的聚类指示矩阵，S为联合类之间相关矩阵．本文不直接针对关系矩阵R进行分解，而是分2阶段实现．

第1阶段针对实体数较少的一类实体X2进行处理，其数量为n．从关系矩阵R中抽取同类实体间的关联关系，进而构建关联矩阵C，矩阵C的规模为n×n．对矩阵C进行对称非负矩阵分解，得到指示矩阵B，如图1（b）所示．由于采用同类实体的关联关系，构建的同质关系矩阵C比原来的关系矩阵R要稠密，在某种程度上能够避免非负矩阵分解中的稀疏性问题，进而提高非负矩阵分解的准确性．

在第2阶段中，将关联矩阵C分解得到的指示矩阵B直接作为关系矩阵R三分解的指示矩阵，如图1（c）所示．在矩阵B已知的情况下，可以很容易计算指示矩阵F和矩阵S．由问题定义可知，矩阵C的规模小于原始关系矩阵R的规模m×n，因此该框架能够处理大规模异构关系数据．

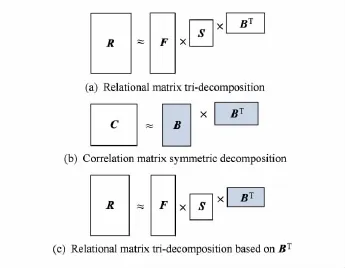
Fig．1 The framework of heterogeneous data co－clustering．图1 异构数据联合聚类框架

3 基于关联矩阵的稀疏联合聚类

根据2阶段非负矩阵分解框架，在异构关系矩阵的基础上，联合聚类主要包括关联矩阵构造、关联矩阵分解、基于关联矩阵的异构关系矩阵三分解3部分．

3．1 关联矩阵构造

在异构关系数据中，选择规模较小的一类实体X2，通过异构关系矩阵R构造X2对应的关联矩阵C．文中利用关联强度Wi，j度量实体X2中任意2个实体xi，xj的关联关系，其可通过2个实体xi，xj基于X1中实体的同现概率进行计算，其计算方法如式（1）所示：

式（2）和式（3）中，N（xi，xj）为X2中的实体xi，xj基于X1中实体同时出现次数．

3．2 关联矩阵分解

通过关联关系构造的关联矩阵C，采用对称非负矩阵分解方法进行分解，其对应的目标函数为式（4）所示：

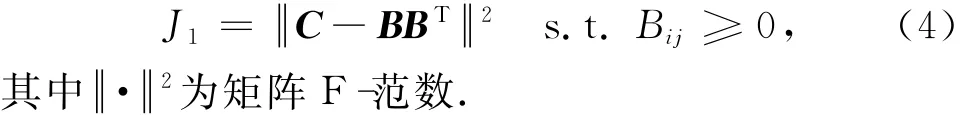
针对目标函数J1，可通过非负最小二乘法进行计算，其计算公式如式（5）所示．基于关联矩阵C的分解结果为聚类指示矩阵B．

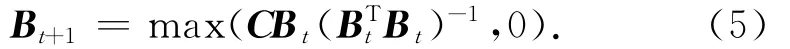
由于聚类指示矩阵中每一个实体只属于一个聚类标签，因此，对矩阵B进行二元化，即B中每一行的最大值对应的聚类结果为1，其余对应的都为0．二元化后的矩阵B将作为关系矩阵R三分解的输入．

3．3 基于关联矩阵的异构关系矩阵三分解

传统的非负矩阵分解通常采用的目标函数如式（6）所示，该目标函数中采用两因子分解法．

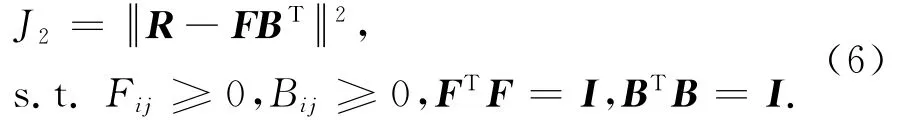
两因子分解法得到的近似低秩矩阵效果较差，因此Ding等人［18］提出了正交非负矩阵三分解，其对应的目标函数为式（7）所示，在目标函数中引入了矩阵S，使得分解得到的矩阵F，B具有实际意义．

由于正交约束条件在某些情况下过于严格，本文中将采用无正交约束的目标函数，如式（8）所示：

对于目标函数J4，现有的方法中常采用乘法更新的迭代求解方法实现，但是其收敛速度较慢．本文将采用快速的迭代求解方法实现，关联矩阵C对称分解得到的矩阵B经过二元化后，直接作为目标函数J4的输入，因此，只需迭代求解矩阵F和S．

在优化求解矩阵S的过程中，固定矩阵F，矩阵S的求解方法如式（9）所示：

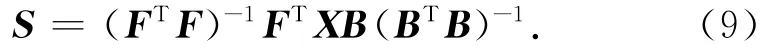
在优化求解矩阵F的过程中，固定矩阵S．由于矩阵F为关系矩阵R的行划分指示矩阵，F中的每一行有且只有一个元素为1，其余为0，因此求解矩阵F的优化问题可按照行进行处理，其转换为式（10）的优化问题．

其中fj·为行聚类指示向量，在该向量中，有且只有一个元素为1，其余的元素都为0，因此，式（10）的优化问题可通过式（11）进行快速求解．

其中珘bk·为SBT对应的第k个行向量．式（10）可通过向量范式枚举法快速求解，避免了使用矩阵乘法迭代更新求解，提高了算法处理速度．

面向大规模异构数据的联合聚类算法的整个过程总结如算法1所示．在关联矩阵C对称分解的基础上对关系矩阵R进行非负矩阵三分解，能够同时解决非平衡和稀疏性问题．算法1中第④～⑨步为异构关系矩阵迭代求解过程．

算法1．异构数据联合聚类算法FNMTF－CM．

输入：R为关系矩阵，聚类数目k，Niter为最大迭代次数，δ为收敛阈值；

输出：F为实体X1聚类指示矩阵，B为实体X2聚类指示矩阵．

4 实验及分析

本文所有实验都在Matlab下实现，硬件平台为曙光8core服务器、8GB内存．

实验中将分别对比算法SS－NMF，FNMTF和本文算法FNMTF－CM．每一组实验分别运行10次，采用随机初始化，最终实验结果中给出平均值．

4．1 实验数据集

本文首先将在联合聚类算法的标准测试数据集［19］①上对算法进行全面的评估．该数据集给出了2类实体的聚类标签，不仅能够针对算法的准确率等指标值进行对比分析，还能对算法在不同聚类难度等级的数据集下进行对比分析．

数据集中共计36组数据，通过贝叶斯错误率Error作为数据集的难度控制参数，包括5%，12%，20%共3个难度等级，其中5%是最容易聚类的数据集，20%是最难聚类的数据集．每1个难度等级分别对应50，100，200，500共4种规模（行和列的规模相同），可针对节点规模进行聚类算法对比分析．每一类节点规模的数据集分别对应3，5，10共3种聚类数目，可针对不同的聚类数进行对比分析．

为了验证FNMTF－CM算法在真实数据集上的效果，将在4个真实的异构关系数据集上进行对比实验．其中Title数据为Sogou提供的新闻标题数据集②，构建新闻标题和词之间的异构关系数据集．Weibo数据集收集了2012年“闯红灯”、“丰田汽车回收”、“美国总统大选”、“莫言获得诺贝尔奖”、“我是特种兵”、“杭州烟花大会”、“中国好声音”7个话题对应的新浪微博消息，经过预处理后得到8 023条微博和374个标签，构建消息和标签之间的异构关系数据集．DBLP1为论文与词之间的关系数据集，DBLP2为论文与作者之间的关系数据集［20］，这2个数据集中分别提取了论文题目和摘要字数超过100个、作者出现多于2次对应的关系数据．4个数据集的详细信息如表1所示：

①https：??www．hds．utc．fr?coclustering?doku．php

②http：??www．sogou．com?labs?dl?tce．html

Table 1 Heterogeneous Relational Dataset表1 异构关系数据集

4．2 评估指标

联合聚类算法的度量指标较多，本文中将采用常见的Purity［21］，NMI［22］，ARI［23］3个指标作为度量标准．对于给定的异构数据集，其中实体规模为n，算法得到的聚类结果为C＝｛c1，c2，…，cK｝，给定的聚类标签为R＝｛r1，r2，…，rL｝，则3个评估指标分别定义如式（12）、式（13）和式（14）．

NMI值在0到1之间，越接近1，则说明聚类结果越好．

ARI（C，R）＝

该ARI值越大，则聚类结果越好．

4．3 人工数据集实验

在同一规模的数据集下评估算法受不同聚类数目K的影响情况，对比结果如图2所示．所有的算法随着K值的增加，准确率都有所下降，但其他2个指标影响较小．因此，在实际使用的过程中，需要根据数据中的真实情况给定聚类数据K．

图3中为在不同数据规模下的对比结果．随着规模的增加，算法的准确率等指标都随之下降．由于该数据集中2类实体的数目一致，无法发挥FNMTFCM算法的优势，其聚类结果接近于FNMTF算法．

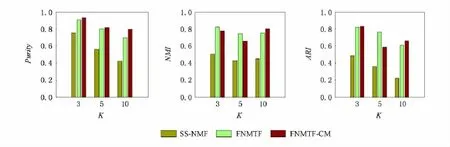
Fig．2 The results of algorithms on the different clustering number K（N＝200，Error＝12%）．图2 算法在不同聚类数K下的对比结果（N＝200，Error＝12%）

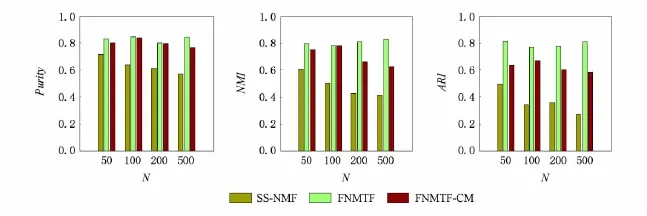
Fig．3 The results of algorithms on the different data scale N（K＝5，Error＝12%）．图3 算法在不同节点规模N下的对比结果（K＝5，Error＝12%）

针对标准测试数据集中不同聚类难度等级的数据集进行算法的鲁棒性对比实验，结果如图4所示．本文算法在处理不同聚类难度等级的数据集时的鲁棒性都优于其他2种算法，这主要是在FNMTFCM算法中降低了数据集本身结构的影响．

4．4 对比实验

为了验证本文算法的效果，在真实的异构稀疏数据集上进行对比实验，在该实验中，设置的聚类数目如表1中所示．

在4个不同的数据集上对比的实验结果分别如表2至表5所示，表中对应的最好结果分别加粗表示．

由实验结果可知，FNMTF－CM算法在4个数据集上的结果整体优于其他2个算法．在Title和Weibo两个数据集上，FNMTF－CM算法的纯度、NMI值和ARI值比其他算法都高．这主要得益于本文算法中基于关联矩阵进行分解，提高了待分解矩阵的稠密度，进而提高了整体算法的准确率．

Fig．4 The results of algorithms on the different clustering difficulty（N＝200，K＝5）．图4 算法在不同聚类难度下的对比结果（N＝200，K＝5）

Table 2 The Result on Title Dataset表2 Title数据集上的对比结果

Table 3 The Result on Weibo Dataset表3 Weibo数据集上的对比结果

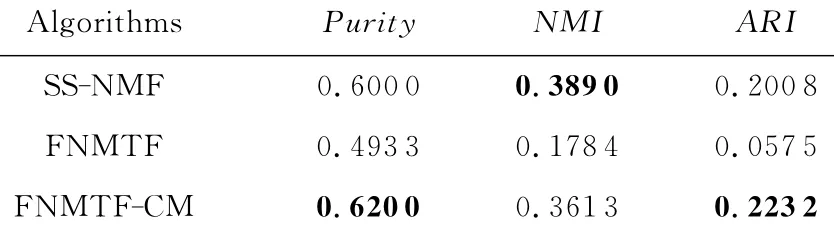
Table 4 The Result on DBLP1Dataset表4 DBLP1数据集上的对比结果

Table 5 The Result on DBLP2Dataset表5 DBLP2数据集上的对比结果

在数据集DBLP1和DBLP2上，SS－NMF算法的NMI值比本文算法要高，特别是在数据集DBLP2上，SS－NMF算法的ARI值也高于本文算法．通过分析可知，DBLP2数据集异常稀疏，该数据集中可能包含较多的奇异点．因此，本文算法在处理奇异点问题上仍有待进一步改进．

进一步分析FNMTF－CM算法在不同聚类数目K值下的效果．在Title数据集中，真实的聚类数目K＝9．该实验中通过调整K值，得到的实验结果如图5所示．由实验结果可知，FNMTF－CM算法在不同的K值下，纯度和NMI值较为稳定，但是在真实的聚类数目下并不是最佳的结果．因此，在实际应用中，需要根据数据选择恰当的聚类数目．

为了说明算法在处理大规模异构关系数据时的处理速度，在Weibo数据集上对3个算法的运行时间进行对比，结果如图6所示．

FNMTF－CM算法的运行时间要小于其他2种算法，主要因为FNMTF－CM算法中选择规模较小的一类实体对应的关联矩阵进行分解，并且求解异构关系矩阵时无需采用乘法更新迭代求解．在微博关系数据中，标签数目比消息数目小很多，因此关联矩阵的规模比原始异构关系矩阵小、处理速度更快．由于SS－NMF算法采用乘法更新迭代求解，收敛较慢，其运行时间最长．

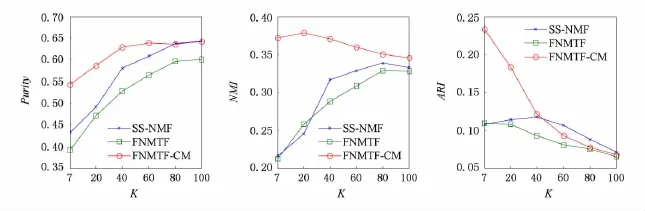
Fig．5 The results of algorithms on different clustering number Kwhen running on Title．图5 在Title数据集上不同聚类数目K的对比结果

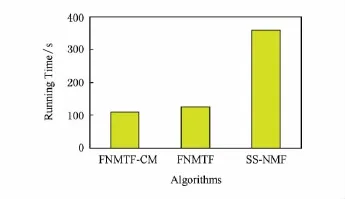
Fig．6 The running time of algorithms on Weibo．图6 算法在Weibo数据集上的时间对比

5 结 论

本文针对大规模异构数据中的非平衡问题和稀疏性问题提出了一种基于非负矩阵分解的联合聚类算法．将传统的联合聚类算法转换成基于关联矩阵的对称分解和基于关系矩阵的三分解，进而实现快速的异构数据联合聚类．实验结果表明本文提出的算法在标准测试数据集和真实异构数据上的效果整体优于其他的算法．

本文算法主要考虑了较小规模实体对聚类的促进作用，下一步将考虑2类实体的相互促进作用．此外，本文只考虑了二阶异构关系，下一步将推广到高阶异构关系数据联合聚类．

［1］Tanay A，Sharan R，Shamir R．Biclustering algorithms：A survey［J］．IEEE Trans on Computational Biology and Bioinformatics，2004，1（1）：24 45

［2］Kemal E，Mehmet D，Onur K，et al A comparative analysis of biclustering algorithms for gene expression data［J］．Briefings in Bioinformatics，2013，14（3）：279 292

［3］Inderjit S D，Mallela S，Modha D S．Information－theoretic co－clustering［C］??Proc of the 9th ACM SIGKDD．New York：ACM，2003：89 98

［4］Inderjit S D．Co－clustering documents and words using bipartite spectral graph partitioning［C］??Proc of the 7th ACM SIGKDD．New York：ACM，2001：269 274

［5］Li Tao，Ding Chris．Non－Negative Matrix Factorizations for Clustering：A Survey［M］??Data Clustering：Algorithms and Applications．London：Chapman ＆Hall?CRC，2013：149 176

［6］Long Bo，Zhang Zhongfei，Yu P S．Co－clustering by block value decomposition［C］??Proc of the 11th ACM SIGKDD．New York：ACM，2005：635 640

［7］Tjhi W C，Chen Lihui，Minimum sum－squared residue for fuzzy co－clustering［J］．Intelligent Data Analysis，2006，10（3）：237 249

［8］Li Zhao，Wu Xindong．Weighted nonnegative matrix trifactorization for co－clustering［C］??Proc of the 23rd IEEE Int Conf on Tools with Artificial Intelligence．Piscataway，NJ：IEEE，2011：811 816

［9］Shang Fanhua，Jiao Licheng，Wang Fei．Graph dual regularization non－negative matrix factorization for coclustering［J］．Pattern Recognition，2002，45（6）：2237 2250

［10］Salunke A，Liu Xumin，Rege M．Constrained co－clustering with non－negative matrix factorisation［J］．Journal of Business Intelligence and Data Mining，2012，7（1?2）：60 79

［11］Chen Yanhua，Rege M，Dong M，et al．Non－negative matrix factorization for semi－supervised data clustering［J］．Knowledge and Information Systems，2008，17（3）：355 379

［12］Chen Yanhua，Wang Lijun，Dong Ming．Non－negative matrix factorization for semisupervised heterogeneous data coclustering［J］．IEEE Trans on Knowledge and Data Engineering，2010，22（10）：1459 1474

［13］Wang Hua，Nie Feiping，Huang Heng，et al．Fast nonnegative matrix tri－factorization for large－scale data coclustering［C］??Proc of the 22nd Int Joint Conf on Artificial Intelligence．Palo Alto，CA：AAAI，2011：1553 1558

［14］Li Tao，Ding Chris．The relationships among various nonnegative matrix factorization methods for clustering［C］?? Proc of the 6th Int Conf on Data Mining．Piscataway，NJ：IEEE，2006：362 371

［15］Gu Quanquan，Zhou Jie．Co－clustering on manifolds［C］?? Proc of the 15th ACM SIGKDD．New York：ACM，2009：359 368

［16］Li Ping，Bu Jiajun，Chen Chun，et al．Relational coclustering via manifold ensemble learning［C］??Proc of the 21st CIKM．New York：ACM，2012：1687 1691

［17］Yan Xiaohui，Guo Jiafeng，Liu Shenghua，et al．Learning topics in short texts by non－negative matrix factorization on term correlation matrix［C］??Proc of the SIAM Int Conf Data Mining．Philadelphia，PA：SIAM，2013：749 757

［18］Ding Chris，Li Tao，Peng Wei，et al．Orthogonal nonnegative matrix tri－factorizations for clustering［C］??Proc of the 12th ACM SIGKDD．New York：ACM，2006：126 135

［19］Lomet A，Govaert G，Grandvalet Y．Design of artificial data tables for co－clustering analysis［R］．Compiègne，France：Universitéde Technologie de Compiègne，2012

［20］Deng Hongbo，Han Jiawei，Zhao Bo，et al．Probabilistic topic models with biased propagation on heterogeneous information networks［C］??Proc of the 17th ACM SIGKDD．New York：ACM，2011：1271 1279

［21］Zhao Ying，Karypis G．Criterion functions for document clustering：Experiments and analysis，UMN CS 01－040［R］．Minnesota，AK：University of Minnesota，2001

［22］Strehl A，Ghosh J．Cluster ensembles—A knowledge reuse framework for combining multiple partitions［J］．Journal of Machine Learning Research，2003，3：583 617

［23］Hubert L，Arabie P．Comparing partitions［J］．Journal of Classification，1985，2（1）：193 218

Shen Guowei，born in 1986．PhD candidate at Harbin Engineering University．His main research interests include data mining，social computing，etc．

Yang Wu，born in 1974．Professor and PhD supervisor at Harbin Engineering University．His main research interests include data mining，information security，etc（yangwu＠hrbeu．edu．cn）．

Wang Wei，born in 1974．PhD and associate professor at Harbin Engineering University．His main research interests include data mining，information security，etc（w＿wei＠hrbeu．edu．cn）．

Yu Miao，born in 1987．PhD candidate at Harbin Engineering University．His main research interests include data mining，social computing，etc（yumiao＠hrbeu．edu．cn）．

Dong Guozhong，born in 1989．PhD candidate at Harbin Engineering University．His main research interests include data mining，social computing，etc（dongguozhong＠hrbeu．edu．cn）．

Large－Scale Heterogeneous Data Co－Clustering Based on Nonnegative Matrix Factorization

Shen Guowei，Yang Wu，Wang Wei，Yu Miao，and Dong Guozhong
（Research Center of Information Security，Harbin Engineering University，Harbin150001）

Heterogeneous information network contains multi－typed entities and interactive relations．Some co－clustering algorithms have been proposed to mine underlying structure of different entities．However，with the increase of data scale，the scale of different class entities are growing unbalanced，and heterogeneous relational data are becoming extremely sparse．In order to solve this problem，we propose a two steps co－clustering algorithm FNMTF－CM based on correlation matrix decomposition．In the first step，the correlation matrix is built with the correlation relationship of smaller－typed entities and decomposed into indicating matrix of smaller－typed entity based on symmetric nonnegative matrix factorization．Correlation matrix has higher dense degree and smaller size compared with the original heterogeneous relationship matrix，so our algorithm can process large－scale heterogeneous data and maintain a high precision．After that，the indicating matrix of smaller－typed can be used as the input directly，so the heterogeneous relational matrix tri－factorization is very fast．Experiments on artificial and real－world heterogeneous data sets show that the accuracy and performance of FNMTFCM algorithm are superior to the traditional co－clustering algorithms based on nonnegative matrix factorization．

heterogeneous network；co－clustering；nonnegative matrix factorization；large－scale data；correlation matrix

TP391

2014－11－24；

2015－03－26

国家“八六三”高技术研究发展计划基金项目（2012AA012802）；国家自然科学基金项目（61170242）

This work was supported by the National High Technology Research and Development Program of China（863Program）（2012AA012802）and the National Natural Science Foundation of China（61170242）．

杨武（yangwu＠hrbeu．edu．cn）

关键词 异构网络；联合聚类；非负矩阵分解；大规模数据；关联矩阵