面向数据融合的半环溯源计算方法

薛见新 申德荣 寇 月 聂铁铮 于 戈

（东北大学信息科学与工程学院 沈阳 110819）（xuejianxin＠research．neu．edu．cn）

面向数据融合的半环溯源计算方法

薛见新 申德荣 寇 月 聂铁铮 于 戈

（东北大学信息科学与工程学院 沈阳 110819）
（xuejianxin＠research．neu．edu．cn）

数据融合是集成数据的质量保证和分析挖掘的前提条件；然而，数据融合作为一个整体对于用户来讲是一个黑盒过程，使得当前数据融合过程缺乏可解释性和可调试性．为了便于数据融合过程中有效的冲突检测和调试，需要利用数据溯源技术建立数据融合的可回溯机制．数据溯源描述了数据产生并随着时间推移而演变的整个过程，半环溯源模型作为一种经典的数据溯源表示形式，不仅能表示结果数据是由哪些数据派生的，而且还能够描述这些数据以什么方式进行派生．主要研究用于数据融合的半环溯源的计算问题．用于数据融合的半环溯源计算是一个pay as you go的模式，计算数据的溯源信息是一个非常耗时的过程．首先，提出一种基于Kleene序列的近似迭代方法，并证明了该方法与半环溯源的派生树定义的关系，从而证明了该方法的正确性．然后，提出了一种类牛顿序列，这种方法比Kleene序列有更好的收敛性．由于递归的引入可能会导致这2种迭代算法无法终止，通过分析结果元组的半环多项式溯源的特点，证明这2种近似算法最坏可在n次迭代后终止．最后，通过实验说明了本文提出的方法是可行和有效的．

数据融合；半环溯源；多项式系统；派生树；递归查询

随着网络的飞速发展，Web技术以其广泛性、交互性、快捷性和开放性等特点迅速风靡全球，并且已经渗入到社会的各个领域，网站及网页数量正以指数级飞速增长．如何准确、有效地集成海量高价值的Web信息，对于诸如市场情报分析、舆情分析、商业智能等分析型应用尤为重要，具有非常重要的应用价值和现实意义．

但是，由于Web信息发布的随意性以及信息发布者的水平差异，使得Web中存在大量不完整、过时、甚至错误、虚假的信息，为了保证集成的准确性，数据融合需要对多数据源的数据进行冲突解决．Web数据融合作为一个整体对用户来讲是一个黑盒过程，这使得当前数据融合过程缺乏可解释性和可调试性．因此，为了使用户能够了解数据来源及演化过程，同时，追踪冲突数据来源以便有效地解决冲突，需要研究一种基于数据溯源的可回溯的数据融合方法．

数据溯源（data provenance）是指数据的产生、并随着时间推移而演化的整个过程的信息，可以为数据融合提供可回溯机制．但是，用于解决数据融合中数据冲突的数据溯源是一种细粒度的pay as you go模型，而当前细粒度的数据溯源方法要么是根据Data lineage［1］的方法计算数据起源，要么是预先计算所有数据的溯源形式［2］．这些方法都不能满足数据融合可回溯机制的要求．

针对现在数据融合过程中透明化、融合阶段比较孤立的特点，同时为了使融合结果具备可解释性、融合过程具备可调试性，需要一种数据溯源方法来实现数据融合可回溯机制，该数据溯源方法应该：

1）是一种细粒度的数据溯源方法，不仅能够表示数据的起源，而且还能够描述数据的生成过程．

2）是一种快速的溯源计算方法，由于数据融合中冲突的解决是一种pay as you go模式，数据融合对溯源计算的实时性要求较高．

很显然基于Datalog查询的半环溯源模型是数据融合可回溯机制的选择．

Datalog查询是合取查询在递归上的一种扩展．近几年Datalog再次成为研究热点，例如基于Datalog的逻辑的表述式语言的大量应用、Internet协议与服务的设计、程序语言的分析与查询、本体的推理与查询等．Datalog查询俨然成为数据交换和数据集成中的一种更具有表达能力的语言．然而，面向Datalog查询的数据溯源的研究还处于起步阶段．其中主要的研究工作是宾夕法尼亚大学提出的半环多项式溯源模型［2］．

半环溯源作为一种典型的细粒度溯源方法，不仅能够追踪结果元组是由哪些数据派生得到的，还能够表示这些数据以什么方式结合派生出结果元组．结果元组的半环多项式溯源信息主要通过结果元组的派生树定义［2］计算得到．这种计算本质上是一种查询的逆操作，需要大量的访问原数据库，尤其是在分布式环境下，计代价很大．然而溯源计算是数据融合可回溯机制的前提，当前的溯源计算方法无法满足数据融合对数据溯源的需求．

本文主要研究面向数据融合的半环溯源计算问题．首先，提出一种近似序列Kleene序列，Kleene序列的第i个值ki等于结果元组的所有高度不高于i的派生树收益．因此，Kleene序列就相当于按派生树的高度对结果元组的派生树进行划分．根据半环溯源模型的派生树定义，结果元组的半环溯源计算可以转换成求解Kleene序列．这种代数方法通过把派生树的构建转化成对相应方程组的近似求解来减少对原数据库的访问，从而大大提高了半环溯源的计算效率．

针对Kleene序列收敛速度较慢的问题，提出了类牛顿序列vi．通过扩展函数在半环域内的可导的语义给出一种类牛顿的方法．由证明可以看出类牛顿序列有比Kleene更好的收敛速度．

然而Kleene序列和类牛顿序列都是一种近似迭代方法，当Datalog查询出现递归时，可能会无限迭代下去．通过分析派生树的结构特性，引入Kleene星操作，最多派生树的高度为n后迭代终止，n表示结果元组的数目．

1 相关工作

数据融合的概念最初来源于多传感器数据融合［3］，是指对来自多个传感器的数据进行多级别、多方面、多层次的处理，从而产生新的有意义的信息．由于需要整合来自不同数据源的异构数据，数据集成很自然地需要进行数据融合的研究．但是对于数据融合的解释还没有一个统一的标准，其中普遍认可的是Dong等人在文献［4］中的解释：数据融合是指将来自不同数据源的表示同一实体的不同表象融合成一种单一的表象，并解决可能存在的数据冲突的过程．

Dong等人［5－8］在数据集成的数据融合方面做了很多具有代表性的工作，他们借助Web网站的拷贝现象，通过建立数据源之间的依赖关系，进而有效地融合多数据源的数据，并设计一个原型系统SOLOMON［9］，以展示数据源之间依赖关系及数据融合过程．

数据溯源是数据管理的重要内容，特别是在Web数据集成中，由于数据源的自由性以及集成过程的多阶段性，更需要追踪数据的起源及其演化过程，以确保集成数据的质量的可解释性和可调试性．

关于数据溯源已经有了大量的研究工作．在传统的异构数据集成方法中，通常使用模式级的数据溯源方法来追踪数据在不同模式间的演化过程．由于数据融合过程中的冲突检查处理的对象是数据，因此，细粒度的数据溯源方法是本文的研究对象．元组溯源是当前数据溯源研究的热点，它在关系表上额外增加一个属性来表示标注信息，用来对元组的元数据进行管理，这些标注信息可以是概率、置信度、布尔变量等．Cui等人提出的lineage溯源［1］方法用来标注哪些元组对结果元组的生成做了贡献．Buneman等人提出的where［10］溯源方法用来表示哪些元组在一起共同构成结果元组．Green等人提出了一种更一般的标注模型——半环溯源（howprovenance［2］）．

对于数据溯源的查询DBNotes［5，11］系统提出一种类似于SQL查询的语言pSQL，用来指定where溯源的传递规则．Trio［12］系统开发了新查询语言TriQL，支持不确定性和溯源查询．Karvounarakis等人［13］提出了一种基于元组、半环溯源的查询语言ProQL，可以很好地实现对溯源信息的查询，同时提供一些机制解决存储和查询的相关问题．Perm［14］是一种数据溯源原型系统，它采用非标注表示法，用查询重写规则来修改SQL查询．文献［15－16］主要研究了数据溯源的查询包含问题．文献［17］提出一种基于circuit的溯源计算方法，这种方法是面向布尔查询，主要是利用布尔电路递归地计算溯源信息，该方法可以在多项式时间构建多项式大小的溯源信息．

2 半环溯源与问题描述

在这节首先介绍Datalog查询和半环溯源的一些相关概念．

2．1 Datalog查询

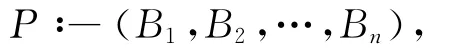
一个Datalog查询通常包含一系列如下形式的规则：这里n≥0，P表示这个Datalog规则的头部，B1，B2，…，Bn的表示Datalog规则的主体．本文假定读者对Datalog已有足够的了解，不再赘述．

关系在Datalog规则中由谓词表示．每个谓词拥有固定数目的参数，一个谓词和它的参数一起被称为原子．实质上，谓词就是一个返回布尔值的函数名．对于Datalog规则中的谓词可以分为扩展谓词（EDB）和内涵谓词（IDB），扩展谓词的关系存放在数据库中，内涵谓词的关系是由一个或多个Datalog规则计算出来的．

2．2 半环多项式溯源

作为一种一般的抽象溯源模型，半环溯源模型是在不完整数据库、概率数据库基础上抽象出来的，是不同溯源模型应用的一个统一框架．文献［6］给出了一个统一的数据溯源框架K关系，即提出一个半环溯源表示模型，溯源的传播是根据关系代数的演算得到的，和查询的耦合度较高．下面给出K关系的定义．

定义1．假设有一个半环K＝（κ，＋，×，0，1），包含2个演算操作符＋和×以及特异元0，1．U表示关系表上的属性集．那么U上的K关系是指一个函数R：U．tuple→κ，其中它的支持元组集supp（R）＝｛t｜R（t）≠0｝．

半环溯源模型是用半环多项式来表示结果数据的生成过程．其中溯源多项式中的×操作对应关系代数中的连接操作，＋操作对应关系代数中的union操作．这样就可以通过多项的结构表示结果数据是由哪些数据通过什么方式生成的．例如一个结果元组t的标注是xy2＋z＋z，其中x，y，z分别表示源数据库中元组的抽象标注，这个多项式表示元组t是由3种派生路径生成，一种是通过x标注的元组与y标注的元组做连接操作生成的，别外2种派生路径是由z标注的元组直接生成．K关系本质是关系半环到标注半环的一个映射关系．

下面给出半环多项式溯源的基于派生树的定义．

定义2［2］．给出一个可交换半环（κ，＋，×，0，1），一个数据库实例D，查询Q∈Datalog≠，Datalog≠表示存在不等式谓词的Datalog查询，对于Q（D）中的任意元组t，其多项式溯源可以表示为：

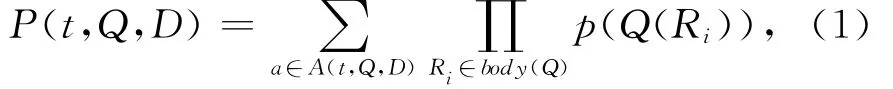
其中A（t，Q，D）是产生t的所有派生树集合．

定义2不仅仅说明了半环溯源的语义，同时也给出半环溯源的计算方法．

2．3 派生树

派生树是本文提出的方法的关键，本文中派生树的概念来源于上下文无关文法．

下面介绍一个在ω－连续半环域内的关于幂级数向量f的派生树，如果没有特殊说明，本文中的半环都是指ω－连续半环．派生树中每一个结点都标注为（X，j）的形式，其中X∈χ表示f中的变量，j表示该结点依赖幂级数哪个项进行派生，它本质上表示一种项的索引．如果一个派生树t的结点是（X，j），映射λ（t）（X，j）表示该派生树与根结点的映射，λv（t）X表示根节点的变量，λm（t）j表示该结点按幂级数中的哪个项派生．

下面将给出关于多项式方程组的派生树定义，并介绍如何定义每个派生树的收益．

定义3．幂级数向量f的派生树和派生树的收益可递归地定义为：

如果向量f的任一单项式mx，j中都是常量（终止符），那么派生树t只包含一个被标记为（X，j）的结点，同时派生树t的收益Y（t）＝mx，j．

如果单项式mx，j＝a1X1a2X2…akXkak＋1，k≥1，t1，t2，…，tk是f中的一个项，其中λv（ti）Xi；那么以t1，t2，…，tk作为子树的树t同样也是f的派生树，如果λ（t）（X，j），那么Y（t）＝a1Y（t1）a2Y（t2）…akY（tk）ak＋1．

定义4．派生树t的高度h（t）表示由根结点到叶子结点的最长的路径长度．为了表示方便，用根结点表示派生，t＝h表示根结点为t的高度为h的所有派生树集合，t＜h表示根结点为t的所有高度小于h的派生树集合．

2．4 问题描述

为了更形象地说明半环溯源计算问题，下面给出实例来详细说明．

给出Datalog查询如图1（a）所示，源数据库实例抽象标注形式如图1（b），图1（c）表示查询结果实例．通过Datalog查询，能够生成如图1（d）所示的固定点方程组．其中结元组的实例表示变量，源数据实例表示常量．最终求解的结果就是用表示常量的源数据库实例来表示结果元组的标注．

当前关于半环溯源的一些研究工作［12］是假定已知如图1（d）所示的等式，这个等式是表示各数据库元组之间的关联关系．数据溯源的查询、传播与存储等研究都是建立在这个派生关系的基础上．生成结果元组与原数据实例之间关系的过程就是计算元组间的派生关系．因此溯源计算过程是半环溯源的研究基础．相同关系内不同元组的派生路径并不相同，因此元组的溯源计算过程以元组为处理对象．结果元组的溯源计算是一个复杂而耗时的过程，由于数据融合中对时效性要求较高，因此需要快速而高效的溯源计算方法．

Fig．1 Provenance for result tuples．图1 结果元组溯源实例

当前Web数据更新与演化比较频繁．而当数据经过多次演化后，多项式溯源的项会指数倍增加，这将导致溯源信息量过大，使得溯源计算过程更加复杂，而快速的计算溯源信息就成为一种挑战．

递归的引入会使得溯源计算过程更加复杂化．递归导致一些元组会重复地派生自身，结果元组的溯源表达式是形式幂级数．面向递归查询的溯源信息计算代价很大，同时溯源信息的存储将会占用更多空间．解决递归查询引起的无穷溯源问题是半环多项式溯源计算专有的问题．

3 Datalog查询与多项式方程组

第2节给出了结果元组的半环多项式溯源的定义，显然这个定义不是一个有效的计算方法．因此，这种半环多项式的派生树定义只可以用来作为理论证明．从Datalog查询评估的角度来看，会存在一个固定点理论．正如溯源信息的Datalog查询一样，会存在一种与派生树定义等价的固定点语义，这种定义具有更好的可计算性．

根据Datalog查询评估的特点，可知结果元组可能会由其他IDB元组派生得到，因此，为了方便表示，对每一个结果元组使用新的变量来表示．因此，通过Datalog规则可以构建结果元组与所有其他元组之间的一个等价关系．

这种等价关系的构建可以在查询执行时构建．但是，一方面需要重写查询机制；另一方面查询执行过程并不能完全反映结果元组的派生路径，比如递归，因为递归查询的终止条件是两次的查询结果相同；而且，数据融合过程中的冲突检测是一个pay as you go模型，只有需要时才会计算相应数据的溯源信息，这种在查询过程中预先计算所有数据的溯源信息方法会大大降低查询的执行效率，也会计算很多不需要的溯源信息并占用大量的存储空间．本节提出一种查询逆操作的方程组构建方法．

定理1．利用Datalog查询构建结果元组的多项式方程组是一个NP－hard问题．

证明．多项式方程组的构建主要利用Datalog查询找出结果元组与其他元组之间的等价关系，如果Datalog规则是合取式的话，那么这个问题可规约为SAT问题，显然是一个NP－complete问题．所以，利用Datalog查询构建结果元组的多项式方程组至少是NP－complete问题．证毕．

对于一个NP－hard问题要从算法的角度优化该问题是比较困难的，但是可以从减少输入的角度来优化该问题．

为了简化概念，假定只存在一个EDB谓词和一个IDB谓词．对于给定的有限的EDB谓词k－关系可以按如下方法（算法1）构建固定点方程组：

算法1．GenerateEquations．

输入：查询Q，IDB元组I，EDB元组E；

输出：固定点方程组．

算法1主要致力于通过Datalog查询规则构建结果元组与其他元组之间的等价关系．首先对于每个EDB元组和IDB元组都赋予一个变量来唯一表示这个元组（行③④）．EDB元组变量在固定点方程中表示常量，而IDB元组变量在固定点方程中表示变量．算法1的关键就是找出IDB变量与其他所有变量之间的等价关系．这种等价关系就是根据Datalog查询找出所有能派生出IDB元组的EDB元组的赋值．由于这个问题超出本文的范围，在另一篇文章中将有详细的解决方法．

4 基于Kleene迭代的半环溯源计算方法

第3节介绍了结果元组半环多项式溯源计算到固定点方程组的转换．那么是不是有可能有一种对方程组的处理方法能够有效地计算结果元组的半环多项式溯源？对固定点方程组的求解显然要比根据结果元组的派生树定义直接构建派生树要有效得多，因为可以避免大量对原数据库的访问．

定理2．给定源数据库实例S、目标数据库实例T、Datalog查询规则q．那么，由算法1构建的固定点方程组的解等于结果元组的半环多项式溯源．

证明．根据Kleene定理可知，在ω－连续半环内求解多项式方程组X＝f（X），存在Kleene近似序列，使得方程组X＝f（X）的解等于这个序列的上确界，而Kleene序列可以迭代地表示为k0＝0，ki＋1＝f（ki）．显然Kleene序列可以看成是一种迭代的方程组求解方法．为了证明定理，只需要证明Kleene迭代与结果元组的派生树的关系．证毕．

引理1．固定点方程组的第i个Kleene迭代ki等于高度不大于i的所有变量的派生树的收益之和．

证明．可以通过归纳法来证明．下面的Hi表示度不高于i的所有派生树集合．

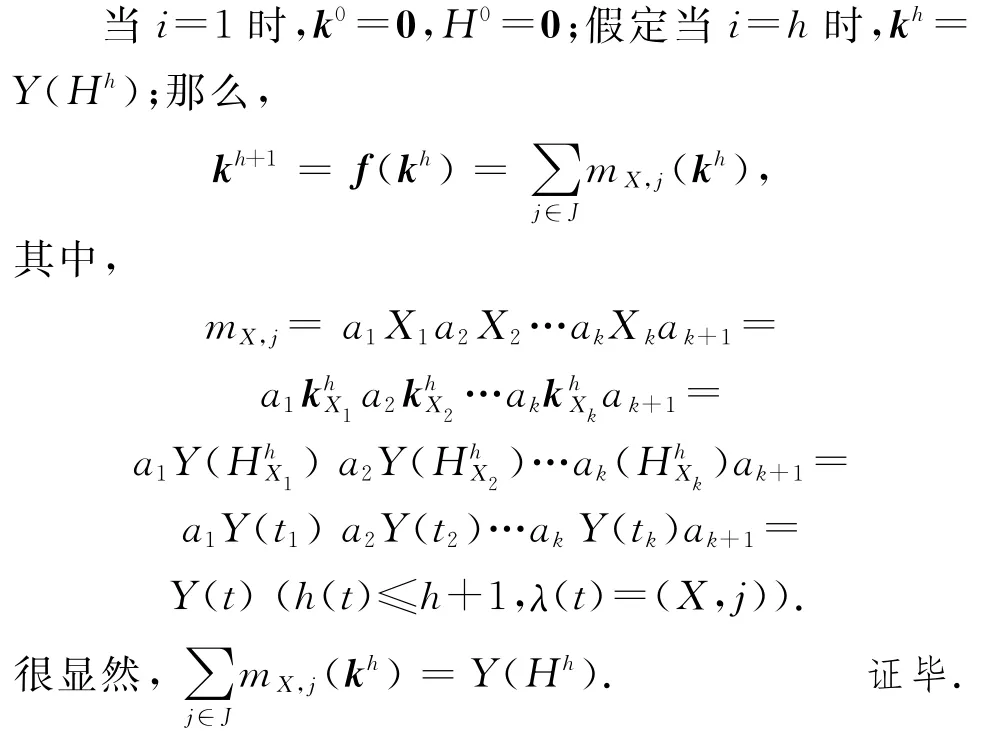
由于固定点方程组的变量表示的是IDB元组的标注，因此，Kleene序列就相当于按派生树的高度来构建结果元组的派生树．根据定义2，可知由算法1生成的于固定点方程组的解就是结果元组的半环多项式溯源信息．

定理2的证明不仅说明了半环多项式溯源的计算可以转化成一种数学计算，而且还给出了一种近似迭代的半环溯源计算方法．这种方法可以避免大量的访问数据，因此，能有效地提高半环多项式标注的计算过程．

5 类牛顿迭代的半环溯源计算

由v0开始，按vi＋1＝vi＋Δi迭代地计算，其中Δi是线性固定点方程Df｜vi（X）

尽管Kleene迭代方法是一种通用方法．但是对于递归查询来说可能无法终止，并且收敛速度较慢．

牛顿迭代是数值域内求解非线性方程组的一种经典方法，它本质上是将非线性方程逐步转换成线性方程来求解，是平方收敛的．那么在半环域内是不是能够有一种迭代方法能快速地收敛．

把牛顿迭代的思想扩展到半环域内，由算法1得到的固定点方程组的一般形式为：

x1＝f1（x1，x2，…，xn）；

x2＝f2（x2，x2，…，xn）；

xn＝fn（x1，x2，…，xn）．

这种方程组可以表示成向量的形式X＝f（X）．计算X＝f（X）的最小解就相当于计算g（X）＝0，其中g（X）＝f（X）－X．

利用牛顿迭代求解方程组，给出可导函数g1，g2，…，gn：Rn→R，求解半环多项式溯源方法就是计算方程组g（X）＝0的解，其中g＝（g1，g2，…，gn）；存在这样一个序列vi＋1＝vi＋Δi，其中Δi是如下线性方程组的解：最小解．这个序列的极值就是原方程组的解．

然而牛顿迭代到半环域内的没有可导函数，这里扩展了半环域内的函数的可导性．

定义5．f是半环域S内的形式幂级数，其中X∈χ是其中的变量．关于变量X的在v点的微分函数DXf｜v（X）：v→S定义如下：

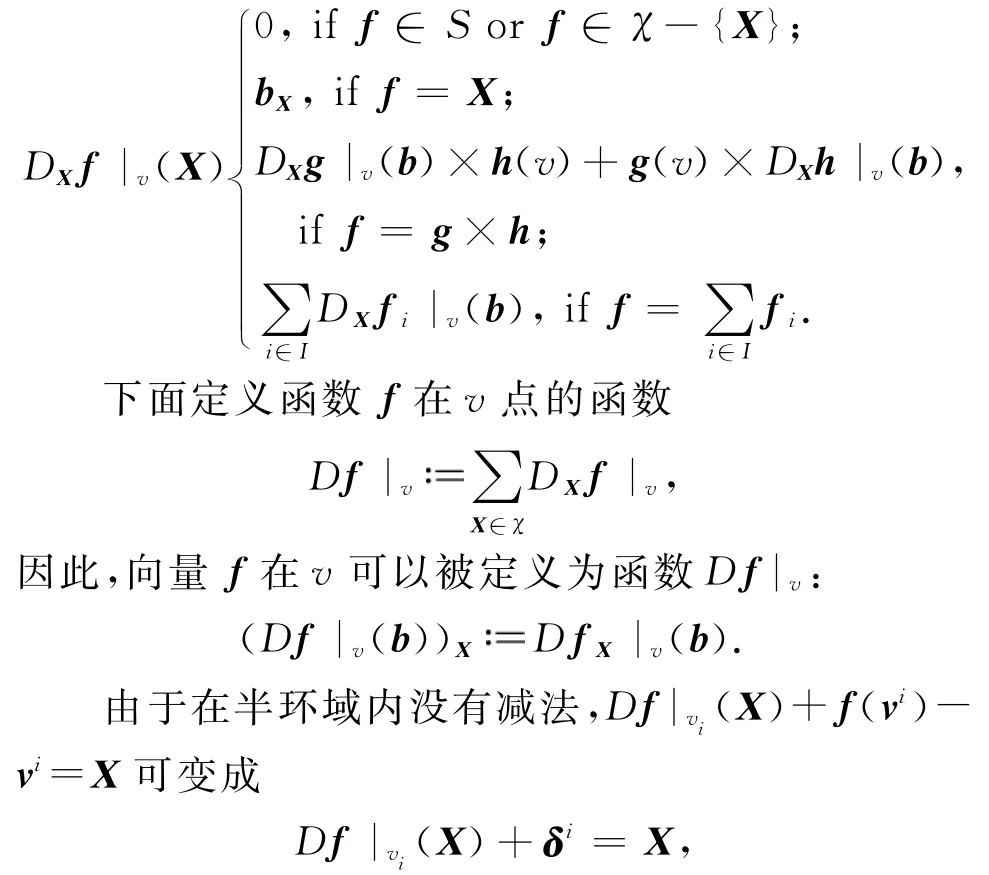
其中δi是满足方程f（vi）＝vi＋δi的取值．

定义6．f是一组形式幂级数的向量，第i个类牛顿近似vi可以被归纳地定义为：

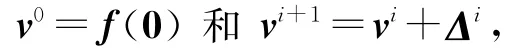
其中Δi是方程Df｜vi（X）＋δi＝X的最小解，δi是满足方程f（vi）＝vi＋δi的任意取值，序列vi被称为类牛顿序列．

给出近似迭代方法类牛顿序列，下面给出类牛顿序列与Klenne序列的关系．

引理2．f：V→V是一组形式幂级数的向量，其中u，w∈V，那么Df｜u（X）＋w＝X；的最小解是Df｜＊u（w）．相似地，类牛顿序列可以被定义为w0＝f（0）和wi＋1＝wi＋Df｜＊vi（δi）．

f（u）＋Df｜u（v）≤f（u＋v）≤f（u）＋Df｜u＋v（v）．

证明．对于由于f一组形式幂级数的向量，可以假定ρ表示向量f中的一个元素，那么ρ一般形式ρ＝g×χ×a，其中，g表示单项式，χ表示变量，a表示常量．

定理3．f是一组形式幂级数的向量，那么只会存在一个类牛顿近似vi，满足如下性质：

ki≤vi≤f（vi）≤vi＋1≤μf＝supkj．

证明．首先证明对于所有的i来说会存在一个δi，满足ki≤vi≤f（vi）．利用归纳法证明这个结论：

当i＝0时，结果显然是满足的．那么假定i取任意大于0的整数时也满足，即ki≤vi≤f（vi）．

接下来需要证明vi≤μf．

当迭代次数为0时，显然是满足的，假定当迭代次数为i时也满足：

定理3的证明说明了类牛顿序列比Kleene序列有更好的收敛性，也就是能更快地计算出半环多项式溯源．

由于Kleene序列和类牛顿序列都是一种迭代方法，而当Datalog查询出现递归时迭代可能是无法终止的．

定理4．Kleene序列和类牛顿序列最多可经过n步终止，其中n表示结果元组的数目．

证明．由于第n个Kleene序列表示所有高度不大于n的派生树集合．定理就相当于证明派生树的高度不需要大于n就可以计算出结果元组的半环多项式溯源．证毕．

6 实验结果与分析

本节给出了基于Kleene迭代方法和类牛顿迭代方法的结果元组半环多项式溯源计算的性能测试结果，并与基于派生树构建的半环多项式标注计算方法进行比较．

采用TPC－H Benchmark的数据集来进行测试．TPC－H Benchmark是通过数据库查询性能测试的实验平台，本文在TPC－H Benchmark测试中选用了查询结果中不包含聚类操作的查询Q2，Q11，Q15和Q20．

此次实验使用的数据库是sql sever 2008数据库，开发工具使用vs2010，系统实现的语言为C＃．6．1 不同数据大小的溯源计算比较

首先考虑的是输入数据大小对各算法的执行时间的影响．选择查询Q2，Q11，Q15和Q20来度量面向不同的查询结果元组的半环多项式溯源计算过程的执行时间．

Tradition方法指的是传统的基于派生树构建的方法，Kleene是指Kleene近似迭代方法，Newton是指类牛顿迭代方法．

由图2中可以看出传统的基于派生树构建的半环多项式溯源计算方法随着元组数的增长计算代价增长较快，而Kleene近似方法和类牛顿近似方法的计算代价随着数据的增长近似线性，可见Kleene近似方法与类牛顿近似方法有很好的计算效率，同时也有很好的可扩展性．

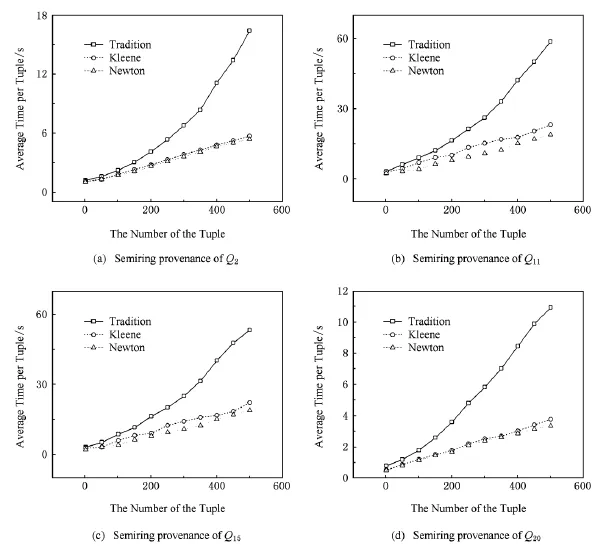
Fig．2 Comparison of semiring provenance with different queries．图2 不同查询的半环多项式溯源计算对比

6．2 合取谓词不同对溯源计算的影响

半环多项式溯源主要是根据Datalog查询找出满足查询的所有元组的组合，本小节测试溯源计算方法面对不同长度的Datalog规则的计算效率．

图3所示为数据大小为1MB，10MB，100MB， 500MB的情况下合取式大小由2～8的计算代价．

通过图3可以看出传统的基于派生树的构建方法代价要远远高于基于Kleene迭代和类牛顿迭代的方法．而随着合取式数目的增加类牛顿迭代表现了更好的性能．

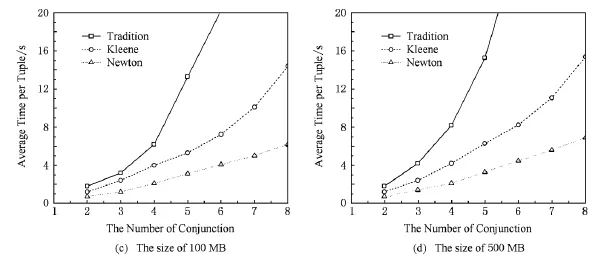
Fig．3 Comparison of semiring provenance with different size of queries．图3 不同查询长度的半环多项式溯源计算对比

6．3 不同演化版本的半环溯源计算分析

针对TPCH数据集构建不同版本的数据，每个版本都可以用实化视图表示．图4中对源数据大小为10MB和100MB两种情况进行了分析比较．半环多项式溯源的计算代价随着版本的增加快速增加，很显然传统的方法增长很快，而随着版本数的增加，类牛顿迭代表现了很好的计算性能和良好的可扩展性．

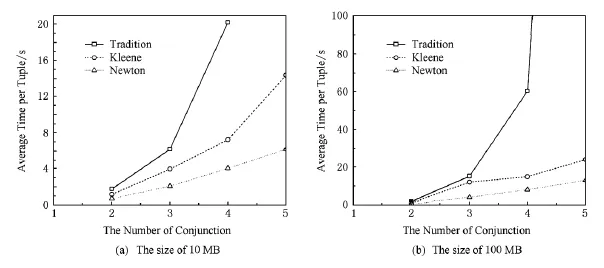
Fig．4 Comparison of semiring provenance with different versions．图4 不同演化版本下的半环多项式溯源比较

7 结束语

针对数据融合过程缺乏可解释性和可调试性，同时为了便于数据融合过程中有效的冲突检测和调试，本文提出了一种基于数据融合的可回溯机制．本文方法致力于研究快速的溯源计算方法，以应对数据融合过程的可回溯机制对实时性的要求．首先提出一种基于Kleene序列的近似迭代方法，该方法通过把对数据处理转换对半环多项式的求解来避免对数据库的大量访问；然后提出一种类牛顿迭代方法通过加速收敛来提高溯源计算效率．通过分析，本文提出的2种迭代方法均收敛．实验结果表明，相对于传统的基于派生树的溯源计算方法，本文提出的2种方法有正好的计算效率，同时随着数据量增长，类牛顿迭代方法有更好的可扩展性．

［1］Cui Y，Widom J，Wiener J L．Tracing the lineage of view data in a warehousing environment［J］．ACM Trans on Database Systems，2000，25（2）：179 227

［2］Green T J，Karvounarakis G，Tannen V．Provenance semirings［C］??Proc of the 27th ACM SIGMOD Int Conf on Management of Data Symp on Principles of Database Systems．New York：ACM，2007：31 40

［3］Llinas J，Hall D L．An introduction to multi－sensor data fusion［C］??Proc of ISCAS 98．Piscataway，NJ：IEEE，1998：537 540

［4］Dong X L，Naumann F．Data fusion—Resolving data conflicts for integration［J］．Proceedings of the VLDB Endowment，2009，2（2）：1654 1655

［5］Dong X L，Gabrilovich E，Heitz G，et al．From data fusion to knowledge fusion［J］．Proceedings of the VLDB Endowment，2014，7（10）：881 892

［6］Dong X L，Berti－Equille L，Srivastava D．Data fusion：Resolving conflicts from mutiple sources［C］??Proc of the WAIM2013．Berlin：Springer，2013：64 76

［7］Li Xian，Dong X L，Lyons K，et al．Scaling up copy detection［C］??Proc of the 31st IEEE Int Conf on Data Engineering．Piscataway，NJ：IEEE，89 100

［8］Xuan Liu，Xin Luna Dong，Beng Chin Ooi，et al．Online data fusion［J］．Proceedings of the VLDB Endowment，2011，4（11）：932 943

［9］Dong X L，Berti－Equille L，Hu Yifan，et al．Solomon：Seeking the truth via copying detection［J］．Proceedings of the VLDB Endowment，2010，3（12）：3 3

［10］Buneman P，Khanna S，Tan W C．Why and where：A characterization of data provenance［C］??Proc of the 8th Int Conf on Data Theory．Berlin：Springer，2001：316 330

［11］Chiticariu L，Tan W C，Vijayvargiya G．DBNotes：A post－it system for relational databases based on provenance［C］?? Proc of the 24th ACM SIGMOD－SlGACT－SlGART Symp on Principles of Database Systems．New York：ACM，2005：942 944

［12］Widom J Trio．A system for integrated management of data，accuracy，and lineage［C］??Proc of the 2nd Biennial Conf on Innovative Data Systems Research．New York：ACM，2005：262 276

［13］Karvounarakis G，Ives I G，Tannen V．Querying data provenance［C］??Proc of the ACM SIGMOD Int Conf on Management of Data．New York：ACM，2010：951 962

［14］Glavic B，Alonso G Perm．Processing provenance and data on the same data model through query rewriting［C］??Proc of the 25th IEEE Int Conf on Data Engineering．Piscataway，NJ：IEEE，2009：174 185

［15］Green T J．Containment of conjunctive queries on annotated relations［J］．Theory of Computing System，2011，49（2）：429 459

［16］Green T J，Huang S S，Loo B T，et al．Datalog and recursive query［J］．Processing Foundations and Trends in Databases，2013，5（2）：105 195

［17］Deutch D，Milo T，Roy S，et al．Circuits for datalog provenance［C］??Proc of the 17th Int Conf on Data Theory．New York：ACM，2014：201 212

Xue Jianxin，born in 1984．PhD candidate．Student member of China Computer Federation．His research interests include recursive query evaluation and data provenance（xuejianxin＠research．neu．edu．cn）．

Shen Derong，born in 1964．Professor and PhD supervisor of the Northeastern University．Senior member of China Computer Federation．Her main research interests include distributed database，Web data management and Web services．

Kou Yue，born in 1980．Associate professor at Northeastern University，China．Member of China Computer Federation．Her main research interests include Web search，Web mining，and dataspace．

Nie Tiezheng，born in 1980．Associate professor at Northeastern University，China．Member of China Computer Federation．His main research interests include data quality and data integration．

Yu Ge，born in 1962．Professor and PhD supervisor at Northeastern University，China．His main research interests include database theory and technology，distributed and parallel systems，and network information security．

Semiring Provenance for Data Fusion

Xue Jianxin，Shen Derong，Kou Yue，Nie Tiezheng，and Yu Ge
（College of Information Science and Engineering，Northeastern University，Shenyang110819）

As an important part of the Web data integration，Web data fusion is the quality assurance of integrated data and the precondition of accurate analysis and mining．However，being a uniform data fusion is treated as black box，which makes the fusion lack of interpretability and debuggable ability．Therefore，to describe fusion process and origin for solving the conflict，we should construct a provenance mechanism with data provenance．Data provenance describes about how data is generated and evolves with time going on，which can not only show which input tuples contribute to the data but also how they contribute．We study the semiring provenance for data fusion．Firstly，we propose an approximate iterative approach to optimal the computational process of semiring provenance．After，to speed up the convergence，we show a Newton－like approach．Recursion may make the situation complicated，we analysize the characteristic of semiring provenance and show that Kleene sequence and Newton－like sequence can convergent only after n step．And experiments show that the technologies in this paper are highly effective and feasible．

data fusion；semiring provenance；polynomial systems；derive trees；recursive queries

TP391

2015－09－25；

2015－11－23

国家自然科学基金项目（61472070）；国家“九七三”重点基础研究发展规划基金项目（2012CB316201）

This work was supported by the National Natural Science Foundation of China（61472070）and the National Basic Research Program of China（973Program）（2012CB316201）．