无线传感器网络DV—Hop定位算法研究

吕元海 王海波

摘 要：基于非测距的DV-Hop定位算法，根据距离未知节点最近的三个信标节点之间的覆盖关系，利用三边测量法估算未知节点的坐标，将传统三边测量法改进后估计未知节点的坐标值，并利用MyEclipse平台进行了仿真实验。实验结果表明，改进的三边测量算法能对无线未知节点的坐标进行有效地定位。

关键词：定位；DV-Hop；三边测量；MyEclipse

中图分类号：TP212.9 文献标识码：A 文章编号：2095-1302（2016）07-00-04

0 引 言

无线传感网络中，在对节点自身定位的研究中[1]，很多改进定位精度的算法被提出来，但由于多种原因例如节点定位带来的开销、大规模无线传感器网络中存在的误差累计等并没有一种完善的DV-Hop算法，因此，包括DV-Hop定位算法在内的很多定位算法仍然需要进一步的研究和探索[2]。

1 网络模型

为了验证改进后的估算未知节点坐标的三边测量法[3]，将其实验平台设置为一个矩形区域，并在此区域内随机部署若干实验节点，作以下要求：

（1）实验中，随机在实验区域内布置出同构的信标节点和未知节点，节点半径均为5 m，每个节点的通信半径为10 m。

（2）为保证网络的连通性，避免不可达节点的出现，尽量保证信标节点和未知节点的分散密集[4]。

（3）每个节点位置均已知。

2 算法设计

2.1 基于求交点的三边测量法

2.1.1 设计思想

基于求交点的三边测量法将三个圆在平面中所形成的交点情况分为四类进行讨论，其中（xi， yi）代表未知节点的坐标值。

（1）三个圆两两相交时，会形成六个交点，如图1所示，将这六个交点的平均值作为未知节点的估计位置，此时（xi，yi）的值使用式（1）计算。

（2）当一个圆同时与其它两个圆有交点时，会形成四个交点，选取如图2所示的四个交点两两连线，连线的长度分别为d1，d2，d3，d4，选出长度最小的直线，用它两个端点的均值作为未知节点的估计位置，采用式（2）计算。

（3）三个圆中只有两个圆相交时，如图3所示，计算出两圆交点后再分别计算出这两个交点与第三个圆圆心的距离d1，d2，将距圆心距离小的点的坐标值作为未知节点的估计位置，按式（3）计算。

（4）当三个圆没有任何交点时，这种情况依然利用基于求交线的三边测量法来计算未知节点的估计距离。

2.1.2 算法流程图

基于求交点的三边测量法流程如图4所示。

2.2 基于求交线的三边测量

将三个圆在平面中的位置关系分为两类：内含和其它，以此为基础将三个圆之间形成的交线分为三种情况讨论。其中（xi， yi）代表未知节点的坐标值，三个圆的圆心坐标为（x1， y1），（x2，y2），（x3，y3），半径为r1，r2，r3，所对应的三个圆的方程如式（4）所示：

圆的方程两两相减求出直线如式（5）所示：

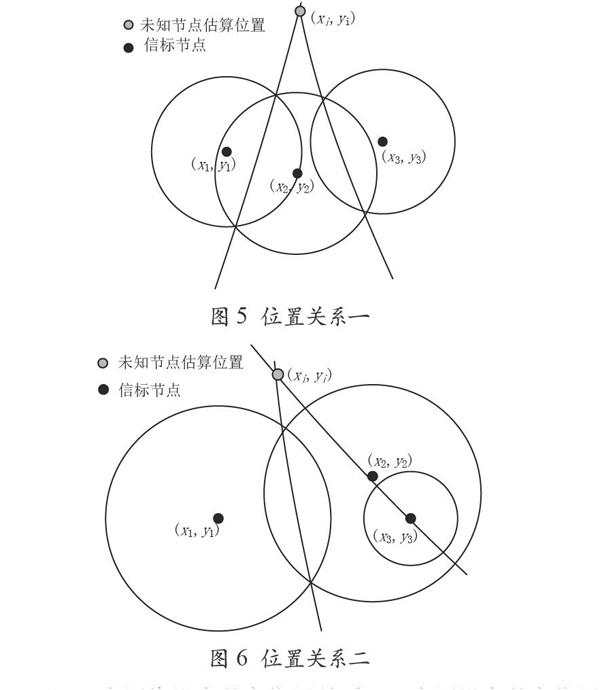
（1）三个圆中两组圆的位置关系均为其它。图5所示以两条直线的交点作为未知节点的估计位置。

（2）三个圆中一组圆的位置关系为其它，如图6所示，求出交线后，在任选两个圆的圆心，求过两个圆圆心的直线，求出交点。

（3）三个圆均没有其它位置关系。三个圆没有其它位置关系的情况非常少见，即三个圆均存在内含关系，如图7所示。在这种情况下估算未知节点坐标时，选取两组圆心间的连线形成交点，在实验中发现，由于此位置关系的特殊性，三个信标节点的距离非常相近，在这种计算方式中，三个信标节点的任一信标节点坐标会被视为未知节点的估计位置。形成交点时，此交点作为未知节点的估计位置，如果出现没有交点的情况，那么未知节点将无法定位，所以这种位置关系的定位精度相对较差[5]，特殊情况下甚至无法定位。

2.3 算法流程图

基于求交线的三边测量法流程如图8所示。

3 仿真实验与性能分析

3.1 仿真实验

本实验通过在MyEclipse中编写Java代码来模拟上述算法的仿真实验，模拟区域参数设置为70 m×70 m，在实验区域内部署30个同构的信标节点和100个同构的未知节点，节点半径为5 m。在实验过程中，为了测试所写算法对定位精度的影响，首先保持信标节点个数不变，将未知节点的个数分别设置为100、200、300、400、500。再保持未知节点个数不变，将信标节点的个数分别设置为10、20、30、40、50。实验平台如图9所示。

3.2 性能分析

在实验过程中，计算出未知节点的估计坐标后，由于生成坐标时未知节点的坐标是已知的，计算出估计的坐标值与实际的坐标值之差越小，证明估算误差越小。

定位误差随未知节点变化的趋势如图10表示，增加未知节点的个数，通过两种算法计算出的各个未知节点的估计坐标与实际坐标之差的平均数，从图中折线图的走向来看，此时基于求交线的三边测量法的定位平均误差在不断增大，而基于求交点的三边测量法的平均误差保持稳定，增大幅度较小，且基于求交点的三边测量法的平均误差始终比基于求交线的三边测量法的平均误差小。

定位误差随信标节点变化的趋势如图11所示，保持未知节点数目不变，逐渐增多信标节点的个数为10，20，30，40，50，计算出平均误差后整理出折线图，可以从折线图的走势看出，两种定位算法的平均误差都在逐渐减小，但基于求交点的三边测量法的平均误差始终小于基于求交线的三边测量法的平均误差，并且下滑趋势快，所以，随着信标节点数目的增多，基于求交点的三边测量法的定位精度优于基于求交线的三边测量法。

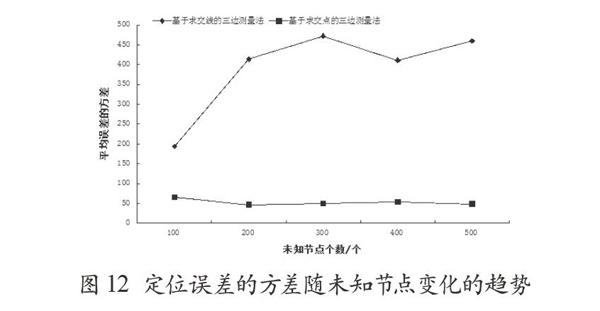
定位误差的方差也可作为定位精度的参考，方差在通常情况下表示的是数据波动性的大小，在本实验中，平均误差的方差所代表的是某一定位方法中定位精度波动的大小。定位误差的方差随未知节点变化的趋势如图12所示，使用平均误差的方差时，随着未知节点个数的增加，基于求交线的三边测量法平均误差的方差始终大于基于求交点的三边测量法平均误差的方差，并且基于求交线的三边测量法的方差整体呈增大趋势，而基于求交点的三边测量法的方差保持稳定。由此可知，未知节点个数增多时，基于求交线的三边测量法对于单个节点定位的误差波动逐渐增大，而基于求交点的三边测量法的定位精度保持稳定，比较具有可靠性。

定位误差的方差随信标节点变化的趋势如图13所示，保持未知节点的个数不变，随着信标节点个数的增加，两种算法所求得的平均误差的方差均逐步减小。基于求交点的三边测量法对每个未知节点的定位误差的波动较小，而基于求交线的三边测量法在定位误差上波动比较大。总体上，基于求交线的三边测量法平均误差的方差始终大于基于求交点的三边测量法的平均误差的方差。

由实验可以看出，平均误差在保持未知节点的数目不变时，改变信标节点数目，信标节点数目越多，定位的精度越高，根据研究数据可知，综合平均误差来看，两种算法均优于传统三边测量法，但基于求交点的三边测量法的定位精度高于基于求交点的三边测量法，故可得出结论，基于求交点的三边测量法的定位精度较高。

4 结 语

本文设计了基于RSSI实现网络目标定位的条件概率定位算法和均值定位算法，通过仿真实验证明，这两种算法都能够实现无线传感网络中未知节点的定位，但在同等环境下，条件概率定位算法在稳定性、平均误差和定位精度等方面均优于均值定位算法。本文的研究仅基于二维空间，具有一定的局限性，下一步将在三维空间中实现未知节点的定位问题。

参考文献

[1]王珊珊，殷建平，蔡志平，等.基于RSSI的无线传感器网络节点自身定位算法[J].计算机研究与发展，2008，45（S1）：385-388.

[2]李成岳.基于DV-Hop的无线传感器节点定位算法研究[D].长春：吉林大学，2011.

[3]秦小虎，辛云宏，夏海峰，等.无线传感器网络节点定位技术[J].计算机系统应用，2011，20（9）：117-121.

[4]催逊学，左从菊.无线传感器网络简明教程[M].北京：清华大学出版社，2009：17-19.

[5]赵文辉，姜宇，刘大昕.高精度无线传感器网络节点定位算法[J].哈尔滨工程大学学报，2009，30（4）：466-471.