加卷积窗测量电气参量时的噪声误差研究

曹堃锐++刘梧林++丁海洋

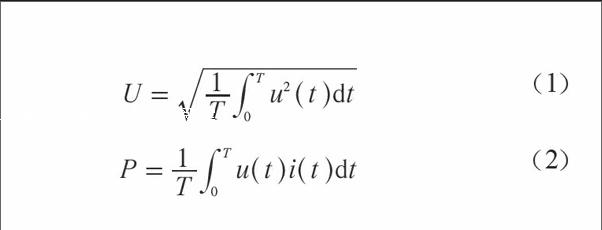
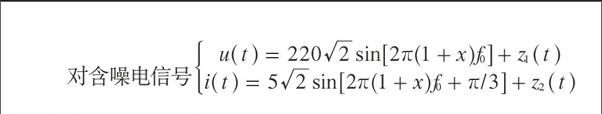
摘 要：采用卷积窗加权法能够基本消除电气参量测量时的不同步采样误差，但却无法降低噪声带来的测量误差。文中研究了加卷积窗测量电气参量时噪声带来的误差问题，研究得出：该测量误差与信噪比及采样频率的开方成反比；根据随机噪声具有的统计特性，提出了对实际测量值进行数理统计运算，以计算量的增大换得噪声引起的误差减小；最后通过数值模拟验证了所提理论的有效性。

关键词：电气参量；卷积窗加权测量法；噪声；误差

中图分类号：TM732 文献标识码：A 文章编号：2095-1302（2016）07-00-04

0 引 言

以微处理器为基础的电工测量仪表在测量有效值、有功功率等电气参量时，信号频率的不稳定会带来不同步采样误差[1，2]。许多学者就克服这种测量误差进行了研究[3-8]，但各种方法都有其侧重点与局限性。文献[9]提出的电气参量卷积窗加权算法，可基本消除不同步采样的测量误差，且权函数有固定解析式，算法简单便于实现。但对于加权算法计算电气参量时，干扰噪声带来的误差问题却没有进行详细的研究。在测量过程中，发现噪声永远存在于电力系统中，其对测量带来的误差往往不能忽视，尤其对强度较弱的电流信号而言[10]，一点噪声干扰可能就使系统的信噪比很低、误差很大。因此本文在简单阐述了卷积窗加权算法的基础上，重点推导了电气参量加权测量中的噪声误差公式，并给出了相应的减小误差的方法。该方法对于解决电气参量高精度测量中的实际问题具有借鉴和指导意义。

1 电气参量的卷积窗加权测量法

设交流电信号u（t）、i （t）的周期为T，则有效值及有功功率为：

在电信号采样过程中，会出现不同步误差，导致用（1）、（2）式计算有效值时，使得信号周期T只能用一近似值T0代入。设x为相对频偏，即T0=（1+x）T；f=（1+x）f0。对电信号加卷积窗可有效克服不同步带来的误差，为便于数值模拟，对加窗后的有效值及有功功率进行时间上的离散。

设N为一个估计周期T0中的采样点数，采样序列记为un、in，相应的卷积窗序列为wk，则有效值及有用功率的加权离散表达式为：

列出了常用的1～3阶卷积窗函数解析式[7]，见式（5）～（7）所示：

2 电气参量加权测量中噪声误差分析

2.1 有效值的噪声误差分析

以电压信号u（t）为例进行说明。随机高斯白噪声假设为z（t），其离散采样序列为zn，为在加噪声z（t）条件下得到的电压有效值，则根据式（3）可得：

式中Uz为噪声信号的有效值，ξ是电压与噪声信号的相关系数，与信噪比SNR（dB）有关，不同SNR下的ξ值分别为：

由于高斯白噪声的随机性，每个采样点zn可以认为服从N（0，σ2）的正态分布，而高斯白噪声信号的标准差等于其有效值Uz，则有：

其中，Pu、Pz分别为电压信号及噪声信号的有功功率，SNR为信噪比。

通过以上计算可以得出：

不同采样点的噪声误差可以看成是相互独立无关的，则信噪比一定时，电压有效值的期望和方差为：

其中，Ak定义与上节相同，主要依赖于权系数的阶数k，有A1=1.00，A2=1.15，A3=1.29[11]。信噪比一定时，由噪声随机性引起的电压有效值与噪声有效值之和的测量相对误差为：

式中fS为采样频率，T0为额定周期（T0=1/f0）， ξ由式（9）确定。

同理可得，电流有效值与所加噪声有效值之和的测量相对误差为：

通过式（15）、式（16）可以看出，加入高斯白噪声引起的测量相对误差反比于信噪比及采样频率的开方根，而增大卷积窗阶数k会使Ak也增大，故只使误差略微减小。

2.2 有功功率的噪声误差分析

设电压信号为u（t），电流信号为i（t）。zn1、zn2分别为电压、电流的噪声信号离散采样序列，为在噪声条件下得到的有功功率，则根据式（4）有：

对于zn1、zn2序列可以认为服从N（0，σ2）的随机正态分布，根据式（11）可以得出：

式中SNR1、SNR2分别代表电压信号、电流信号的信噪比（dB）。

电压与电流的噪声信号zn1、zn2是相互独立无关的，可得出以下推导：

不同采样点的噪声误差可以看成是相互独立无关的，则有功功率的期望和方差为：

其中，Ak、Ak1、Ak2定义与上节相同（、），在给定权系数的阶数k后，Ak1=Ak2=Ak，且有A1=1.00，A2=1.15，A3=1.29[11]。因此由于噪声而造成的有功功率测量的相对误差为：

式中fs为采样频率，ψ为功率因数的真值。

通过式（22）可以看出，加入高斯白噪声引起的测量相对误差反比于信噪比及采样频率的开方根，而增大卷积窗阶数k会使Ak也增大，故只使误差略微减小。

3 降低噪声误差的方法

由上节可知，直接测量出的有效值应在综合有效值（真有效值与噪声有效值之和）上下一定范围内随机得出，且信噪比越小，波动范围越大。但信噪比低于一定值时，波动范围大小将基本不变。同时噪声信号与电信号的不相关性，使得式（15）中的综合有效值波动不会太大。由此，我们可以求出多个周期的有效值大小，再通过其期望和方差，联立式（13）、式（14）建立二元一次方程组，求出真有效值与信噪比大小。

假设在信噪比不变的情况下，采样了3n个周期，每三个周期加三阶卷积窗权系数求一次有效值，则将得到n组有效值，记为Ui（i=1，2，…，n），建立方程组有：

若在计算前能大概估出信噪比范围，则直接利用式（9）确定相关系数ξ，否则可先按ξ=1代入计算信噪比，再进行调整即可。endprint

由于加了三阶卷积窗权系数求其有效值，故不同步误差可忽略。这时由式（23）算出的电压、电流真有效值的主要误差为：在信噪比一定时，有限个数Ui所求出的均值、标准差的实际值与理论值之间不相同所带来的计算误差。根据上面的分析，可以通过以下办法提高计算的精度：

（1）在信噪比不变的情况下，增加采样周期，使得原有效值Ui的数量增多，这样Ui的均值及标准差将更接近理论值。此办法的可行性在于只需考虑计算量因数，而不用考虑频率偏差是否变化。

（2）通过硬件设备降低系统的信噪比，这样可使Ui围绕综合有效值的波动范围减小，求出的均值及标准差更准确。

（3）增加采样频率，式（15）采样频率的增大也会使Ui误差的波动范围减小。

与有效值的方法类似，在信噪比不变的情况下，对电压、电流信号分别采样 3n个周期，加三阶卷积窗权系数求出n组有功功率值，记为 （Pi（i=1，2，…，n）），其均值为：

根据式（20）可知， 便是所要求的有功功率值。若要进一步提高计算精度，可做与有效值类似的处理。

4 数值模拟

4.1 有效值仿真

为验证本节理论的有效性，对加白噪声的电信号进行数值仿真：

式中的z（t）代表随机生成的标准高斯白噪声信号[12]。在电力系统中信号频率的波动范围一般为49.5～50.5 Hz，取f0=50 Hz，则相对频偏|x|<0.01。各次谐波的振幅（V）与初相位（rad）见表1所列。

假设量化位数足够高，因此，不考虑量化误差。图1列出了采样频率 ，卷积窗阶数k=3，信噪比SNR=120、50、8、0、 -8、-20（dB）时相对频偏与综合相对误差的关系仿真图，点状直线为式（15）算出的理论噪声误差，曲线或折线为实际综合误差，花点为不同步采样造成的误差（信噪比较低时可忽略）。由图中可以看出两点：

（1） 由于干扰噪声的随机性，实际误差值以理论估计值为中心上下波动，说明理论公式可以估计真实的情况，具有实际应用性；

（2）随着信噪比的降低，综合有效值的误差逐渐增大，但极低信噪比下，变换趋势却很缓慢。

在仿真条件不变的情况下，表2列出了常用信噪比下利用式（23）在不同测量次数时，求得的有效值与真值的绝对误差大小（V）。信号的真有效值为U=220.064 V。

可以看出，使用式（23）可以很好的求出电信号有效值大小，且随着测量次数的增多，所求的结果越准确。

4.2 有功功率仿真

对含噪电信号

进行数值仿真，以验证本节理论的有效性。在电力系统中，f0=50 Hz，相对频偏|x|<0.01。取采样频率fs=3 200 Hz，权阶数k=3。

假设量化位数足够高，不考虑量化误差。随机选取几组电压、电流的信噪比SNR1、SNR2对有功功率及功率因数测量中因噪声引起的相对误差进行仿真，如图2所示。点状直线为式（22）算出的测量误差的理论估计值，折线为实际测量误差。可以看出：由于干扰噪声的随机性，实际误差值以理论估计值为中心上下波动，说明理论公式可以估计真实的情况，具有实际应用性。

在前提条件不变的情况下，表3列出了在不同测量次数时，求得的有功功率与真值的绝对误差大小（W），有功功率的真值为P=550 W。可以看出，测量出的有功功率次数越多，求出的均值越接近于其真值。

5 结 语

在基于三阶卷积窗加权算法的电气参量测量中，不同步采样引起的误差基本可以忽略不计，这时干扰噪声引起的测量误差将变得重要，尤其对于某些小信号而言。从推导出的噪声误差关系式中可以看出，测量误差与采样频率的开方及信噪比成反比。根据噪声具有的随机性特征，可通过数理统计的相关知识降低其信噪比，以改善电气参量的测量精度。数值模拟结果说明，对电气参量测量的次数越多，求出的均值越接近于各参量的真值。因此需在计算量与测量精度之间做折中选择。

参考文献

[1]李沂乘.采样计算方法测量交流电压有效值误差分析[J].电子测量与仪器学报，2008（ZJ）：62-65.

[2] Kampik M，Laiz H， Klonz M.Comparison of Three Accurate Methods to Measure AC Voltage at Low Frequencies[J].IEEE Trans.on IM，2000，49（2）：429-433.

[3]郑势，王秋光，石雨涛.采用小波变换的有效值和频率测量方法[J].电子应用，2007，26（2）：101-103.

[4]葛庆庆，邵天章.交流电信号有效值高精度测量算法研究[J].电测与仪表学报，2012，49（11）：11-14.

[5]赵明旭，周佩娟.交流模拟量参数精确测量仪表设计[J].东北电力技术，2011（6）：36-37.

[6]龙军.三相电气参量快速和高精度的测量算法[J].传感器技术，2004，23（8）：63-65.

[7] ZHANG Yu，HE Qiu-rui.Weak Signal Detection Based on Phase Locked Loop and Chaotic Oscillator[J].Electrical Measurement & Instrumentation，2012，49（559）：38-40.

[8] Liu Ya-dong， Yang Hong-geng， Ma Chao， et al.An Adaptive Measuring Method for Frequency Signal[J].Transactions of China Electrotechnical Society，2012，27（11）：263-270.

[9]张介秋，陈砚圃，梁昌洪，等.交流电电气参量高精度测量的加权算法[J].仪器仪表学报，2005，26（2）：172-176.

[10]洪磊，谢川，李玉玲，等.基于新过采样方法的APF电流THD测量[J].电力电子技术，2011，45（1）：96-98.

[11]张介秋，梁昌洪，陈砚圃.卷积窗及其在电力系统参量估计中的应用[J].电子学报，2004，32（12）：2013-2016.

[12]张萍，戴光明.高斯随机噪声实时生成实现方法研究[J].电子技术应用，2004（4）：10-12.endprint