基于多目标遗传算法的高速履带车辆动力学模型参数修正研究

王钦龙，王红岩，芮强（装甲兵工程学院机械工程系，北京100072）



基于多目标遗传算法的高速履带车辆动力学模型参数修正研究

王钦龙，王红岩，芮强
（装甲兵工程学院机械工程系，北京100072）

摘要：为了提高高速履带车辆多体动力学模型仿真结果的准确度，对模型参数修正方法进行了研究。建立了高速履带车辆多体动力学模型，根据其行驶工况统计规律，选择水泥路和砂石路作为参数修正的行驶路面条件。对比分析了模型参数修正前的仿真结果与实车测试结果，并给出了修正目标函数的表达式。通过正交实验设计筛选出对目标函数影响较大的待修正模型参数。为了解决修正效率低、计算量大的问题，建立了修正参数与目标函数之间关系的径向基神经网络近似模型。通过分析目标函数随修正参数的变化规律，采用多目标遗传算法NSGA-Ⅱ对两种工况条件下的模型参数同时进行修正，并确定了最终解。研究结果表明，动力学模型仿真结果的准确度得到了提高，证明该修正方法的有效性。

关键词：兵器科学与技术；高速履带车辆；参数修正；多目标遗传算法；径向基神经网络

0　引言

由于虚拟样机技术的多体动力学建模及仿真是当前研究高速履带车辆行驶平顺性、操纵稳定性以及越野机动性等动力学性能的一种重要方法［1-3］，而动力学性能分析结果是否可信直接取决于所建立的动力学模型的准确程度。在建模过程中，由于模型的简化、参数测量误差等因素的影响，所建立的多体动力学模型与实际车辆之间必然存在一定的差异，为了缩小这种差异，需要对车辆多体动力学模型的参数进行修正，从而提高其动力学性能分析结果的准确度［4］。

车辆多体动力学模型参数修正就是通过某种优化算法在参数设计空间中进行搜索，获得使动力学模型的仿真结果与实车测试结果最接近的模型参数，从而提高模型仿真结果的可信性和准确度。

本文以某型高速履带车辆为研究对象，根据其行驶工况的统计规律，分别选取车辆在水泥路和砂石路两种典型路面并以30 km/h匀速行驶作为模型修正的工况条件。首先建立高速履带车辆多刚体动力学模型，对比分析两种工况条件下参数修正前的仿真结果与实车测试结果，初步验证动力学模型的可信性并确定修正目标函数的表达形式；其次，利用正交实验设计筛选出待修正的模型参数；为解决修正效率低、计算量大的问题，建立了待修正参数与目标函数之间关系的径向基神经网络近似模型；最后，通过分析目标函数随修正参数的变化规律，采用多目标遗传算法NSGA-Ⅱ对上述两种工况条件下的动力学模型参数同时修正，获得Pareto前沿并确定参数修正的最终解。相关技术流程如图1所示。

1　高速履带车辆多体动力学建模

1.1模型的拓扑结构分析

某型高速履带车辆主要由上装与车体系统、动力传动系统和行动系统等组成，其中行动系统包括主动轮、负重轮、托带轮、诱导轮及曲臂型张紧机构、履带板、履带销及悬挂装置弹性元件和阻尼元件等。建模时，主要以行动系统为主，其中，在保证履带张紧力符合实际的前提下，张紧机构的传动装置简化为滑柱和套筒，二者采用移动副和弹簧阻尼力进行约束，传动装置与车体、曲臂之间分别采用球副和圆柱副进行约束，曲臂与车体、诱导轮之间分别采用旋转副进行约束，以保证张紧机构与诱导轮之间具有确定的运动关系。其他子系统与车体合并为一个刚体系统模型。首先根据部件之间的约束关系，对模型进行拓扑结构分析，如图2所示，各部件和约束明细见表1和表2.

图1　模型参数修正技术流程Fig.1 Updating process of model parameters

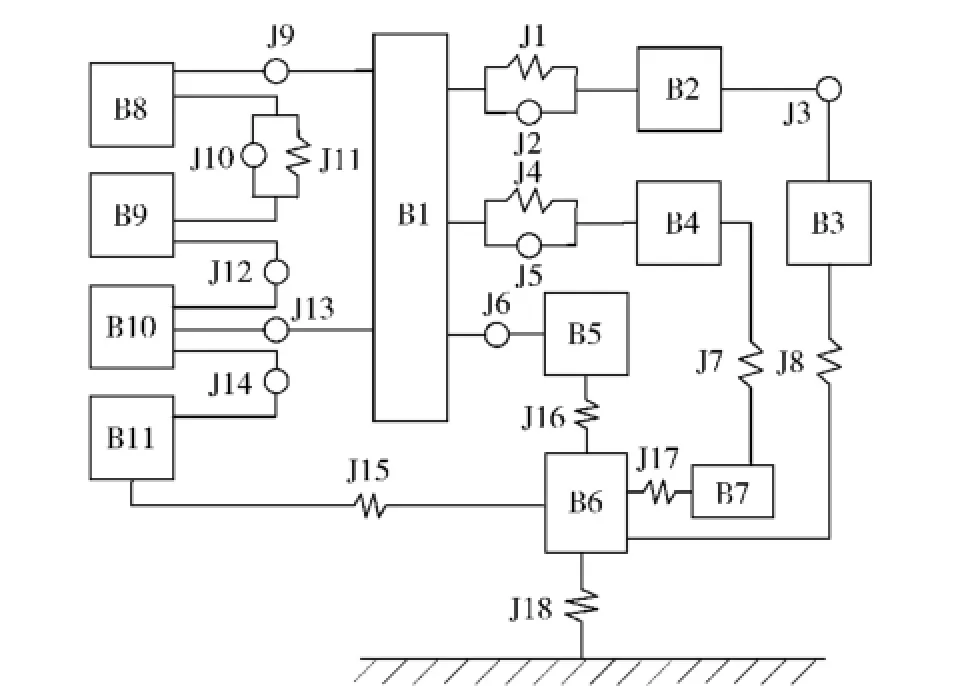
图2　模型拓扑结构图Fig.2 Topological structure of model

分析图2、表1和表2可知，建立动力学模型共需部件数目为427，位移约束数目为54，其中旋转副、球副、移动副和圆柱副限制自由度分别为5、3、5和4，模型总自由度数目为2 348.

表1　部件明细表Tab.1 Parts list

表2　约束明细表Tab.2 Constraint list

1.2力约束描述

在图2中，约束J1为作用在平衡肘和车体之间的弹簧阻尼力矩，通过对悬挂系统的扭杆弹簧-叶片式减震器等效得到［5-6］，等效公式为

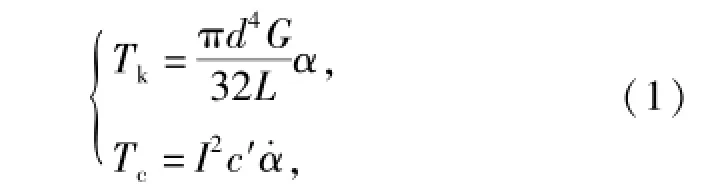
式中：Tk和Tc分别为等效弹簧力矩和等效阻尼力矩；d为扭杆弹簧直径；G为扭杆弹簧剪切模量；L为扭杆长度；I为减震器拉臂至平衡肘安装点的传动比；c′为减震器阻尼系数；α为平衡肘转动角度变化量，α·为其变化率。

在高速履带车辆中，主动轮、负重轮、诱导轮及托带轮与履带间的相互作用力按接触力处理，即约束J7、J8、J15和J16，其计算公式为

式中：″为接触力；τ和ε分别为接触刚度系数和阻尼系数；e为接触力非线性指数；δ为接触广义距离，其变化率为；δ1为产生接触力的临界距离。

履带板与地面之间的相互作用力按接触-摩擦力约束处理，即J18，其中接触力计算公式同（2）式，摩擦力计算公式为

式中：″μ为摩擦力；v为履带板与地面之间的相对滑动速度；vs为静摩擦转换速度；vd为动摩擦转换速度；μs为静摩擦系数；μd为动摩擦系数；Nμ为履带板与地面间的正压力。

主动轮驱动力矩约束J4根据具体工况条件进行定义，其余力约束（J11和J17）按线性弹簧阻尼力处理，计算公式较为简单，限于篇幅，不再赘述。

1.3位移约束描述

动力学模型中任一部件广义坐标可表示为

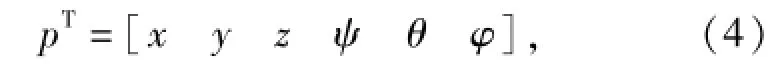
式中：x、y、z为笛卡尔坐标系下的部件质心坐标；ψ、θ、φ为质心坐标欧拉角。以模型中应用最多的旋转副为例，对其进行位移约束描述，由于旋转副限制3个方向的相对位移和两个方向的相对转角，因此，其位移约束方程可表示为

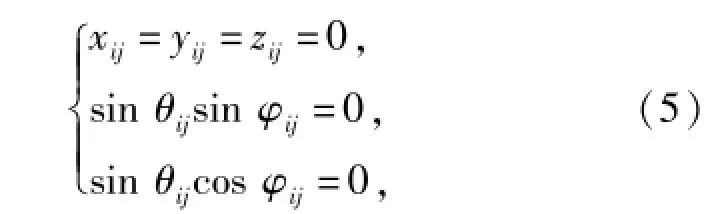
式中：xij、yij、zij为部件i相对部件j在3个方向的位移分量；ψij、θij、φij为部件i相对部件j的欧拉角。

1.4路面建模

高速履带车辆行驶路面以砂石路和水泥路最具有代表性，是车辆的典型行驶路面，为了使模型参数修正结果具有较好的适应性和普遍性，本文选择某车辆试验场的水泥路和砂石路作为模型修正的行驶路面条件，根据国家标准GB7031的规定，对两种路面实测路面谱进行拟合，路面谱拟合表达式为

式中：Gq（f）为路面不平度空间频率f对应的功率谱密度；fl和fu分别为f的下限和上限；Gq（f0）为路面不平度参考空间频率f0对应的标准功率谱密度，f0=0.1 m-1；w为频率指数，是路面功率谱密度与空间频率在双对数坐标下的比例系数。根据（6）式，路面不平度可表示为

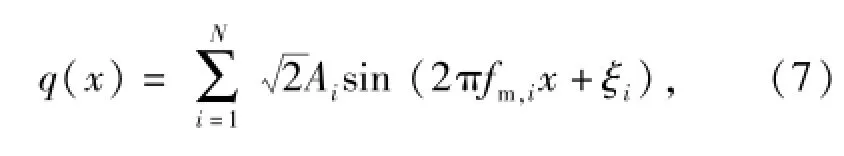
式中：q（x）为路面纵向距离x对应的路面不平度；ξi为N个在［0，2π］区间均匀分布的随机数；fm，i为在［fl，fu］内划分的N个区间所对应的中心频率，每个区间长度为Δf；Ai为对应谐波的振动幅值，即

根据路面不平度序列，构造路面节点矩阵和单元矩阵，并生成代表水泥路和砂石路的动力学仿真路面模型［7］，如图3所示。

图3　随机路面模型Fig.3 Simulation model of random road surface

1.5整车多体动力学模型

采用基于广义笛卡尔坐标系的第一类拉格朗日方程建立高速履带车辆多体动力学模型，系统广义坐标矩阵为

式中：n为模型部件数量。对于系统的约束矩阵方程可表示为

式中：m为系统位移约束和力约束方程数目。则动力学模型的欧拉-拉格朗日方程组［8］为

2　模型参数修正目标函数

2.1模型可信性初步验证

在进行参数修正之前，需要对模型的可信性进行初步验证，以保证后续修正计算初始点的准确度。为此，本文以在某车辆试验场进行的高速履带车辆行驶振动试验为例进行研究工作，试验路面选取前述水泥路和砂石路，行驶车速为30 km/h，测试信号为车体前甲板中央处的垂向振动加速度，动力学仿真工况条件与实车试验一致。图5和图6分别为水泥路和砂石路上实车测试结果与动力学仿真结果的加速度功率谱密度曲线对比。

图4　高速履带车辆多体动力学模型Fig.4 High mobility tracked vehicle multi-body dynamic model

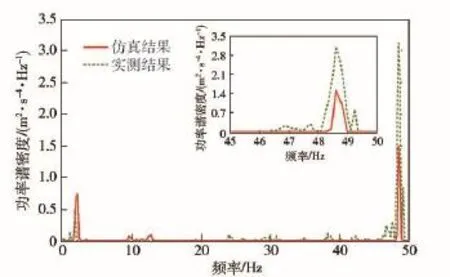
图5　水泥路工况的加速度功率谱密度曲线对比Fig.5 Comparison of PSD curves under the condition of cement road

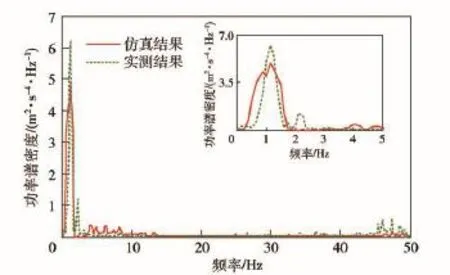
图6　砂石路工况的加速度功率谱密度曲线对比Fig.6 Comparison of PSD curves under the condition of gravel road

由图5可知，水泥路工况下实车测试结果与仿真计算结果的功率谱密度曲线主峰值均在48.5 Hz附近，而由该车履带板节距tT和行驶车速u可知，来自履带板节距的激励频率fT=u/tT=48.3 Hz，说明在水泥路面行驶时，车体振动的主要激励源来自履带板的激励，由于水泥路的路面等级较高，路面不平度对车体振动的影响相对较小。

由图6可知，砂石路工况下实车测试结果与仿真计算结果的功率谱密度曲线主峰值均在1 Hz附近，与车体的振动主频率较为一致。对比图5可知，由于砂石路的路面等级较低，车辆在砂石路面行驶时，车体振动的主要激励源来自路面不平度的激励，履带板的激振对车体振动的影响相对较小。

综上所述，本文建立的高速履带车辆动力学模型具有一定的可信性，仿真结果较为真实地反映了实际车辆的动力学响应特性。

2.2模型参数修正的目标函数

由前述可知，实车测试结果与仿真计算结果的功率谱密度曲线比较相似，但仍然存在一定的差异。造成这种差异的来源主要有：一是建模时对部分设计参数进行了等效简化；二是受加工误差、测量误差以及装配误差等因素的影响，设计参数本身就存在一定的不确定性。因此需要对模型参数进行修正，以提高仿真计算结果的准确度。

由于仿真计算用路面谱是实际路面谱的一致估计，具有较高的统计精度，因此不考虑由于路面谱差异所造成的仿真计算结果与实车测试结果的误差。

参数修正的首要工作是建立修正目标函数，以量化实车测试结果与仿真结果的相似性。由于振动加速度功率谱密度曲线不仅反映了振动能量的总体大小，还反映了信号的频率成分以及各频率成分所对应振动能量的相对大小，因此，采用功率谱密度曲线构造参数修正的目标函数，即

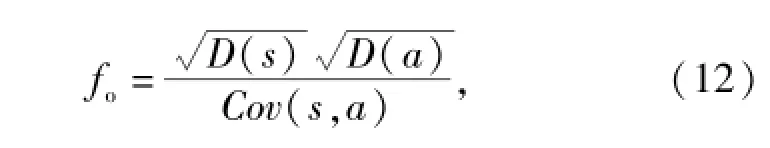
式中：s和a分别是仿真结果与实测结果的功率谱密度；D（s）和D（a）分别是仿真结果与实测结果的方差；Cov（s，a）是仿真结果与实测结果的协方差。fo的取值范围为［1，∞］，函数值越接近1，则表示仿真结果越准确，与实车测试结果越接近。

3　模型修正参数筛选

为了确定对修正目标函数影响较大的参数，以缩小参数设计空间和提高修正效率，本文首先利用实验设计进行参数筛选。根据车辆动力学的相关理论［9］，选取车体主惯量Ixx和Iyy、车体质心纵向位置cmx、车体质心垂向位置cmz、扭杆弹簧刚度系数（该车第1，2，5，6扭杆弹簧刚度系数与第3，4扭杆弹簧刚度系数不同，分别记为k1、k2）以及减震器的等效阻尼系数c进行参数筛选，车体质量一般认为是准确值，故不将其作为修正参数。为保证参数修正后，车体姿态和车底距地高变化不大，参数取值范围设定在［-10%，10%］。

由于筛选参数较多，单次实验仿真计算量较大，故采用L8（27）标准正交表进行7因子2水平正交实验设计，对每组实验参数组合进行动力学仿真，提取仿真结果并根据（12）式计算修正目标函数的响应值，最后计算各参数对应的极差以确定对目标函数影响较大的参数，极差K计算公式为

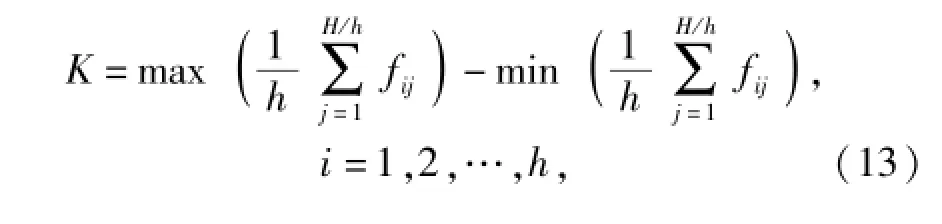
式中：H为实验次数；h为因子水平数；H/h为每个因子水平的实验次数；fij为因子第i个水平的第j次实验所对应的目标函数响应值。不同因子的极差是不同的，极差越大，表明该因子对目标函数的影响程度越大。根据极差计算结果绘制柱状图如图7所示。

图7　两种路面工况条件下模型参数的极差Fig.7 Range of model parameters under two road conditions

由图7可知：在水泥路工况条件下，对目标函数影响较大的参数依次是Iyy、k1和c；在砂石路工况条件下，对目标函数影响较大的参数依次是cmx、Iyy和k1.其中k1和Iyy对两种工况条件下的目标函数影响程度均较大。由于在砂石路工况条件下，cmx的影响程度最大，而参数c的影响程度很小。因此，选取Iyy、k1和cmx作为两种工况条件下的待修正模型参数。

4　径向基神经网络近似模型

4.1径向基神经网络近似模型

由于高速履带车辆多体动力学模型的规模较大，仿真解算时间长、效率低，为解决这一问题，本文采用径向基神经网络构造了待修正参数与修正目标函数之间关系的近似模型，以替代动力学模型复杂的仿真计算，提高修正效率。

径向基神经网络［10-12］是一种高精度的多维空间非线性函数逼近技术，由输入层、隐含层和输出层构成，其中隐含层中神经元的变换函数即径向基函数，是一种对中心点径向对称且衰减的非负非线性函数，其表达式为

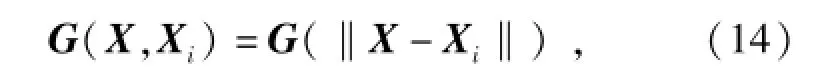
式中：X表示输入向量；Xi为任一隐含层节点径向基函数的中心点，一般选取自训练样本；‖X-Xi‖为欧几里德范数，表示函数值仅与X和Xi之间的欧式距离有关，常采用多元高斯函数表示，即

式中：σ2为高斯函数的方差。则径向基神经网络输出层第j个神经元输出为

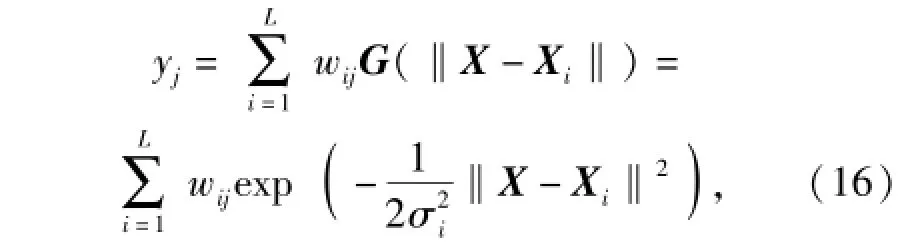
式中：wij为隐含层第i个节点与输出层第j个节点之间的突触权值；L为隐含层节点数目。则整个神经网络输出层的响应为

式中：W=［wij］为输出权值矩阵；G为由（15）式组成的格林矩阵，具有旋转不变性和平移不变性。则权值矩阵W可直接用伪逆的方法求解，即

式中：Y为该神经网络训练样本所对应的期望响应，在本文中，即用于建立近似模型的样本点所对应的修正目标函数响应值。

求得权值矩阵W后，径向基神经网络训练完成，即得到所求近似模型。

首先利用优化拉丁超立方实验设计构造待修正参数的设计空间，参数取值范围与参数筛选一致，一共得到32组修正参数组合，对每组参数组合进行动力学仿真并计算修正目标函数响应值，获得用以训练径向基神经网络的样本组合，利用该样本组合求取权值矩阵并得到修正参数与目标函数之间的近似模型，图8～图13为修正参数初始值处的近似模型，例如，图8为参数k1初始值处的近似模型。

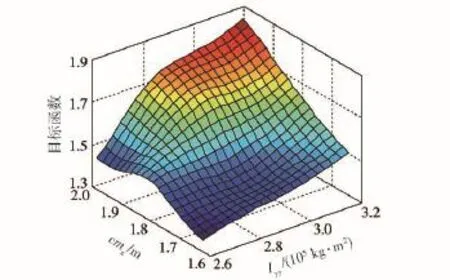
图8　水泥路工况cmx、Iyy与目标函数的近似模型Fig.8 Approximation model of cmx，Iyyand objective function under the condition of cement road

图9　砂石路工况cmx、Iyy与目标函数的近似模型Fig.9 Approximation model of cmx，Iyyand objective function under the condition of gravel road

图10　水泥路工况cmx、k1与目标函数的近似模型Fig.10 Approximation model of cmx，k1and objective function under the condition of cement road

图11　砂石路工况cmx、k1与目标函数的近似模型Fig.11 Approximation model of cmx，k1and objective function under the condition of gravel road

图12　水泥路工况Iyy、k1与目标函数的近似模型Fig.12 Approximation model of Iyy，k1and objective function under the condition of cement road

图13　砂石路工况Iyy、k1与目标函数的近似模型Fig.13 Approximation model of Iyy，k1and objective function under the condition of gravel road

4.2近似模型拟合精度检验

在修正参数设计区间内随机抽取15个样本点，分别利用动力学模型和近似模型得到对应的目标函数真实值和预测值，如图14和图15所示。近似模型拟合精度指标通常采用复相关系数R2表示，即

式中：yi为样本点的真实值；为近似模型在样本点处的预测值；为样本点真实值的均值；S为拟合精度检验所用的样本点个数。R2数值大小在［0，1］之间，一般要求近似模型的R2大于0.9才能满足使用要求，R2越靠近1，则近似模型的拟合精度越高，预测值越准确。经计算，水泥路工况和砂石路工况的近似模型R2分别为0.964 2和0.978 7，说明构建的径向基神经网络近似模型的拟合精度较高，可满足后续参数修正计算的需要。

图14　水泥路工况近似模型预测值与真实值对比Fig.14 Comparison of real value and predicted value of approximation model under the condition of cement road

图15　砂石路工况近似模型预测值与真实值对比Fig.15 Comparison of real value and predicted value of approximation model under the condition of gravel road

5　动力学模型参数修正

5.1目标函数随修正参数的变化规律

分析上述近似模型可知，在整个设计空间内，修正参数与目标函数大致呈单调变化，为更加直观地分析其变化规律，分别在修正参数初始值处选取目标函数随其中一个参数的变化曲线进行分析，如图16～图18所示。

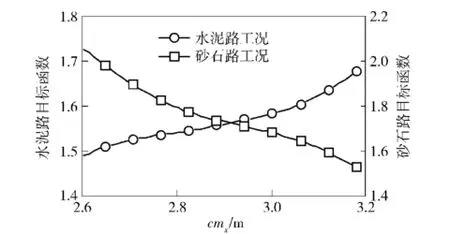
图16　目标函数随cmx的变化曲线Fig.16 Objective functions vs.cmx

图17　目标函数随Iyy的变化曲线Fig.17 Objective functions vs.Iyy

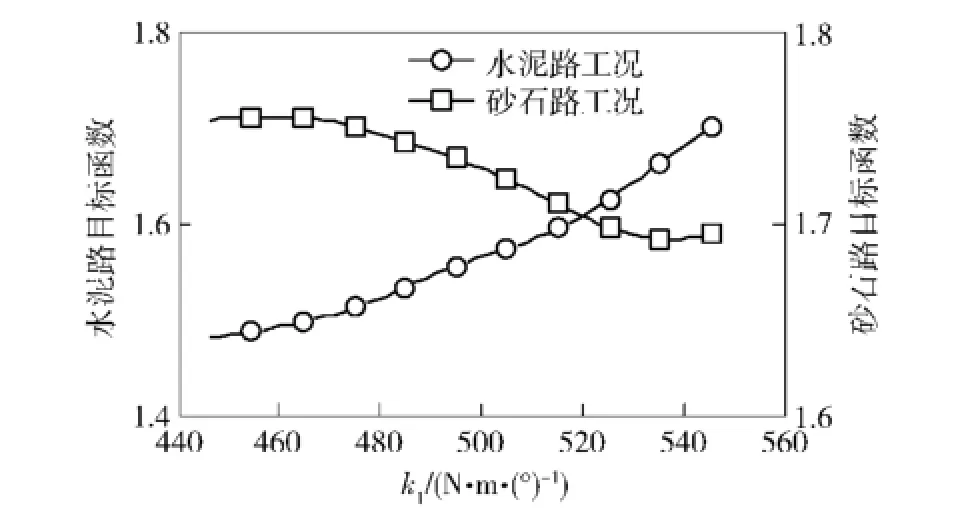
图18　修正目标函数随k1的变化曲线Fig.18 Objective functions vs.k1

由图16～图18可知，虽然水泥路和砂石路工况的目标函数与参数Iyy的变化规律基本一致，但是与参数cmx、k1的变化规律皆相反，说明两种工况的目标函数存在着一定的冲突。若采用传统的单目标优化算法分别对水泥路和砂石路工况的模型参数单独修正，则不能同时取得最优解。因此，本文采用基于遗传算法的多目标修正方法对水泥路和砂石路工况条件下的动力学模型参数同时进行修正。

5.2基于多目标遗传算法的参数修正

动力学模型参数修正的数学表达式为

式中：fo，b和 fo，f分别为水泥路和砂石路工况下的修正目标函数；修正参数上标L、U分别表示参数取值下限和上限，与近似模型的参数设计区间一致。

目前，用于多目标优化问题的遗传算法主要有：邻域培植遗传算法NCGA、存档微遗传算法NSGA、第一代非支配遗传算法NSGA和第二代非支配遗传算法NSGA-Ⅱ等。其中，NSGA-Ⅱ是一种带精英策略的遗传算法，其搜索寻优性能良好，在非支配排序中，接近Pareto前沿的个体被选择，因而其Pareto前进能力强，收敛效率高，是目前求解多目标优化问题最有效的遗传算法［13］。NSGA-Ⅱ的计算流程［14］如图19所示。

图19　非支配遗传算法NSGA-Ⅱ的计算流程Fig.19 Calculation flow of NSGA-Ⅱ

在本文的参数修正问题中，设置初始种群数为12，总进化代数20，共进行240次迭代计算，得到的参数修正Pareto前沿如图20所示。

由图20可知，NSGA-Ⅱ搜索得到的Pareto前沿大致呈一条光滑的曲线分布，前沿表面大多数Pareto最优解均可搜索到，且砂石路工况目标函数的寻优方向与水泥路工况目标函数的寻优方向相反，体现了参数修正问题中两个目标函数与修正参数之间变化规律相互冲突的现象。表3为根据参数修正Pareto前沿得到的部分具有代表性的修正结果及其相对于参数修正前的目标函数变化率。

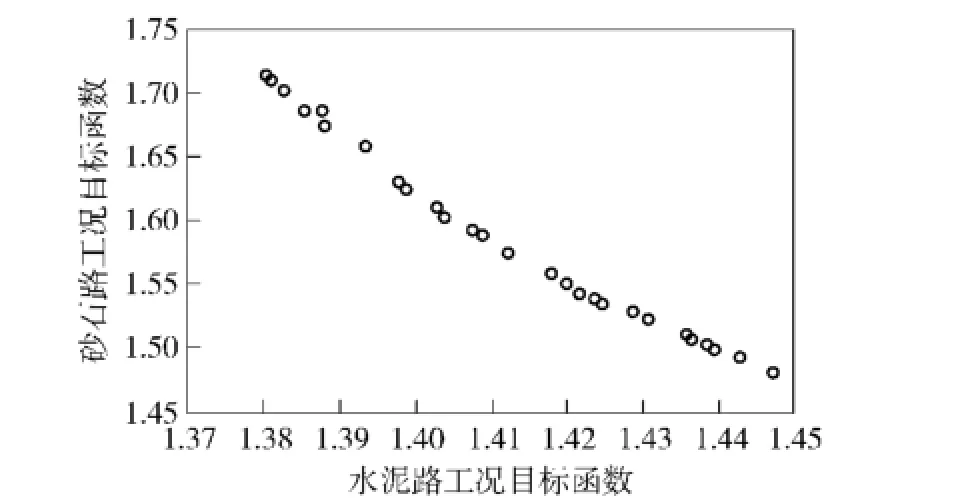
图20　动力学模型参数修正的Pareto前沿Fig.20 Pareto front of dynamic model parameter updating

表3　模型修正结果及变化率Tab.3 Updated results and rate of change

由表3可知，在修正参数的设计区间内，水泥路和砂石路工况目标函数的变化率分别在11.38%～15.01%和2.44%～14.28%之间，虽然水泥路工况第9解的修正效果达到了最佳，但此时砂石路工况的修正效果不明显，只有2.44%，此外，高速履带车辆在实际行驶过程中，砂石路面行驶里程占总行驶里程的比例最高，对车辆动力学性能的影响最大，因此选择砂石路工况条件下修正效果最佳的第1解作为参数修正的最终解。将第1解对应的修正参数代入高速履带车辆多体动力学模型中，重新计算两种工况的动力学响应，并与参数修正前的仿真结果和实车测试结果对比，如图21和图22所示。

由表3、图21和图22可知，与修正前相比，水泥路工况目标函数变化率为11.38%，砂石路工况目标函数变化率为14.28%，修正效果明显，且修正后的功率谱密度曲线与实车测试结果更加接近，从功率谱密度曲线主峰值看，水泥路工况修正后的仿真值相对于试验值的误差由修正前的51.67%减小至13.50%，砂石路工况修正后的仿真值相对于试验值的误差由修正前的21.64%减小至9.88%，说明仿真结果的准确度得到了有效的提高，同时也证明了基于多目标遗传算法的模型参数修正方法的有效性。

图21　水泥路工况修正前后仿真结果与实测结果对比Fig.21 Comparison of test results and simulated results before and after parameter updating under the condition of cement road

图22　砂石路工况修正前后仿真结果与实测结果对比Fig.22 Comparison of test results and simulated results before and after parameter updating under the condition of gravel road

6　结论

本文以某型高速履带车辆为研究对象，针对两种典型随机路面行驶工况，为提高动力学模型仿真结果的准确度，提出了基于多目标遗传算法的模型修正方法，主要结论如下：

1）根据高速履带车辆实车测试结果和动力学仿真结果的对比，初步验证了动力学模型的可信性，并分析了两种工况下车体振动响应的主要激励源。

2）采用正交实验设计对模型参数进行了筛选，该方法直观简单且计算量小，特别适于参数多，计算成本高的动力学模型参数修正问题。

3）根据修正参数随修正目标函数的变化规律，对水泥路和砂石路工况条件下的动力学模型进行同时修正，采用第二代非支配遗传算法NSGA-Ⅱ求解，得到了参数修正的Pareto前沿，并确定了最终解，结果表明：修正后模型仿真结果的准确度得到了明显的提高，证明了基于多目标遗传算法的模型修正方法的有效性。

参考文献（References）

［1］ 韩宝坤，李晓雷，孙逢春.履带车辆动力学仿真技术的发展与展望［J］.兵工学报，2003，24（2）：246-249. HAN Bao-kun，LI Xiao-lei，SUN Feng-chun.Present state and future outlook of the simulation of tracked vehicles［J］.Acta Armamentarii，2003，24（2）：246-249.（in Chinese）

［2］ Ferretti G，Girelli R.Modelling and simulation of an agricultural tracked vehicle［J］.Journal of Terramechanics，1999，36（3）：139-158.

［3］ Rubinstein D，Hitron R.A detailed multi-body model for dynamic simulation of off-road tracked vehicles［J］.Journal of Terramechanics，2004，41（2/3）：163-173.

［4］ 马伟标，王红岩，芮强.基于广义简约梯度算法的履带车辆模型参数修正［J］.系统仿真学报，2012，24（4）：774-779. MA Wei-biao，WANG Hong-yan，RUI Qiang.Researchon model updating for tracked vehicle dynamic model based on generalized reduced gradient method［J］.Journal of System Simulation，2012，24（4）：774-779.（in Chinese）

［5］ 居乃鵕.装甲车辆动力学分析与仿真［M］.北京：国防工业出版社，2002. JU Nai-jun.Dynamics analysis and simulation for armored vehicle ［M］.Beijing：National Defense Industry Press，2002.（in Chinese）

［6］ 丁法乾.履带式装甲车辆悬挂系统动力学［M］.北京：国防工业出版社，2004. DING Fa-qian.Dynamics of tracked armored vehicle suspension system［M］.Beijing：National Defense Industry Press，2004.（in Chinese）

［7］ 王钦龙，王红岩，芮强.轮式越野车动力学建模及行驶动力学特性仿真分析［J］.装甲兵工程学院学报，2012，26（5）：34-38. WANG Qin-long，WANG Hong-yan，RUI Qiang.Dynamic modeling and simulation analysis on ride dynamic of wheeled off-road vehicle［J］.Journal of Academy of Armored Force Engineering，2012，26（5）：34-38.（in Chinese）

［8］ 陈立平，张云清，任卫群，等.机械系统动力学分析及 ADAMS应用教程［M］.北京：清华大学出版社，2005. CHEN Li-ping，ZHANG Yun-qing，REN Wei-qun，et al.Dynamic analysis of mechanical system and application course of ADAMS ［M］.Beijing：Tsinghua University Press，2005.（in Chinese）

［9］ Mitschke M，Wallentowitz H.汽车动力学［M］.陈萌三，余强，译.北京：清华大学出版社，2009. Mitschke M，Wallentowitz H.Dynamic of vehicle［M］.CHEN Meng-san，YU Qiang，translated.Beijing：Tsinghua University Press，2009.（in Chinese）

［10］ Bu D X，Sun W，Yu H S，et al.Adaptive robust control based on RBF neural networks for duct cleaning robot［J］.International Journal of Control Automation and Systems，2015，13（2）：475-487.

［11］ 高隽.人工神经网络原理及仿真实例［M］.北京：机械工业出版社，2003. GAO Jun.Theory and simulation example of artificial neural network［M］.Beijing：China Machine Press，2003.（in Chinese）

［12］ David V，Sánchez A.Searching for a solution to the automatic RBF network design problem［J］.Neurocomputing，2002，42（1）：147-170.

［13］ 李伟平，王世东，周兵，等.基于响应面法和NSGA-Ⅱ算法的麦弗逊悬架优化［J］.湖南大学学报：自然科学版，2011，38（6）：28-32. LI Wei-ping，WANG Shi-dong，ZHOU Bing，et al.Macpherson suspension parameter optimization based on response surface method and NSGA-Ⅱalgorithm［J］.Journal of Hunan University：Natural Science，2011，38（6）：28-32.（in Chinese）

［14］ Chen S M，Shi T Z，Wang D F，et al.Multi-objective optimization of the vehicle ride comfort based on Kriging approximate model and NSGA-Ⅱ［J］.Journal of Mechanical Science and Technology，2015，29（3）：1007-1018.

中图分类号：TJ811

文献标志码：A

文章编号：1000-1093（2016）06-0969-10

DOI：10.3969/j.issn.1000-1093.2016.06.002

收稿日期：2016-01-10

基金项目：军队“十二五”预先研究项目（2011YY18）

作者简介：王钦龙（1987—），男，博士研究生。E-mail：wang_qinlong@126.com；王红岩（1965—），男，教授，博士生导师。E-mail：why_cvt@263.net

Research on Parameter Updating of High Mobility Tracked Vehicle Dynamic Model Based on Multi-objective Genetic Algorithm

WANG Qin-long，WANG Hong-yan，RUI Qiang
（Department of Mechanical Engineering，Academy of Armored Forces Engineering，Beijing 100072，China）

Abstract：A method of model parameter updating is researched to improve the accuracy of simulation results of high mobility tracked vehicle dynamic model.A dynamic model of high mobility tracked vehicle is established，and the cement road and the gravel road are selected for updating the model parameters according to the statistical regularity of the driving conditions.The simulation results of dynamic model without parameter updating and the corresponding real vehicle test results under the same driving conditions are compared and analyzed，and the expression of objective function for model parameter updating is given.The updating parameters which influence objective function strongly are screened by using orthogonal experiment design method.The radial basis function neural network approximation models about the relation among updating parameters and objective functions are established to solve the issues of large calculation quantity and inefficiency of parameter updating.By analyzing the change rule of objective functions with updating parameters，the dynamic model parameters are updated simultaneously by using the second non-dominated sorting genetic algorithm（NSGA-Ⅱ）for two driving conditions.The final resultsof parameter updating are obtained.The research results show that the simulation accuracy of high mobility tracked vehicle dynamic model is effectively improved，and the availability of the proposed method is validated.

Key words：ordnance science and technology；high mobility tracked vehicle；parameter updating；multiobjective genetic algorithm；radial basis function neural network