针对舰艉流抑制的ACLS纵向控制律优化设计
张智, 李佳桐, 董然, 原新
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)
针对舰艉流抑制的ACLS纵向控制律优化设计
张智, 李佳桐, 董然, 原新
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)
摘要:舰艉气流扰动是造成舰载机着舰误差的一个主要因素,因而自动着舰系统需要具有较强的对抗扰流能力。本文借鉴美国F/A-18A飞机自动着舰控制器基本构型,对算例舰载机完成了纵向着舰控制系统优化设计。针对舰艉流随机性分量,利用遗传算法对控制回路参数进行离线寻优,寻优过程兼顾了系统时域性能指标和频域安全边界约束;针对舰艉流稳态分量,在固定参数寻优结果的基础上加入内回路补偿指令以实现控制系统对完整舰艉流的最优抑制;通过仿真验证优化后的控制系统。结果表明,所提出的优化方案可行有效,优化后的自动着舰系统具有更好的指令响应特性以及更强的鲁棒性,提高了舰载机着舰精度。
关键词:舰载机;舰艉流;自动着舰系统;遗传算法;频域安全边界;指令补偿
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20160421.1040.006.html
由于在着舰阶段环境扰动复杂,飞行控制精度要求高,因而舰载机着舰操作难度很大;为减轻飞行员负担,提高舰载机着舰飞行品质,美国海军研制了全自动着舰导引系统(automatic carrier landing system, ACLS)并投入使用[1]。
在设计ACLS时,除了考虑舰载机的机动性,还须特别关注控制系统对进场路径大气紊流(主要指舰艉流)的抑制能力,因为大气扰动是引起着舰误差的主要来源之一[2-3]。为此,美国海军曾在20世纪70年代末开发了以高度变化率(即“H-dot”)为基准反馈信号的ACLS,并将其应用于A-7E,F-14A,S-3A和F/A-18A等舰载机上进行验证,大量测试结果表明,具有H-dot指令模式的ACLS在恶劣流场中展现出良好的鲁棒性[2,4]。另外,在发展着舰控制系统的过程中,美国海军总结了ACLS设计准则,包括时域和频域指标,它们是对舰载机进场和着舰性能的一般规定,并不局限于特定机型[4-5]。
然而,许多针对ACLS控制律优化设计的理论研究工作并没有综合考虑ACLS的性能。例如:文献[6]仅从系统对阶跃指令的响应方面进行控制器参数调校,并未优化系统的扰动抑制能力;文献[7]采用模糊自适应PID参数整定方法改善了基于迎角恒定的动力补偿系统(Approach Power Compensation System, APCS)的性能,但在检验抗风能力时,扰动输入仅选取了用单位阶跃信号代表的垂向突风,它同复杂的舰艉流模型相差很大;文献[8]的研究与文献[7]存在类似问题;文献[9]利用基于模型参考的模糊自适应系统整定了ACLS纵向内回路参数,使纵向ACLS对不同海况下的舰艉流扰动都有良好的抑制能力,文献[10]结合非线性动态逆与滑模控制,通过改善纵向ACLS各个反馈环的性能以实现舰艉流场中舰载机对指令路径的精确跟踪,但这两项研究都未考虑所引入的设计方法对舰载机操纵性能的影响;文献[11]利用有限界H∞方法综合了F/A-18A飞机H-dot控制律,但令人满意的验证结果仅是ACLS对垂直速率指令以及对舰艉流垂直分量的响应。此外,以上这些研究都忽视了设计ACLS时应满足的频域边界问题。
为使ACLS具有良好的指令响应性能和鲁棒性,并且满足频域设计边界,本文将F/A-18A飞机H-dot指令构型应用于某型舰载机,利用遗传算法技术完成ACLS纵向控制律的优化设计并通过仿真验证了结合参数寻优和指令补偿后的ACLS的时域性能。
1舰艉流模型
本文采用军标MIL-HDBK-1797所描述的舰艉流工程化模型对着舰阶段大气环境建模。该模型将扰流速度矢量分为水平纵向分量u、水平横向分量v和垂向分量w。u与甲板风Vw/d的方向平行,向前为正;v沿驾驶员右手方向为正;w向下为正[12]。并且,根据舰艉流特性,分为4部分建模,每部分的速度都能在上述3个方向上分解,即:自由大气紊流分量由u1、v1和w1组成;舰艉流稳态分量由u2和w2组成;周期性分量由u3和w3组成;随机性分量由u4、v4和w4组成。计算完整的舰艉流速度[12]:
(1)
1.1自由大气紊流分量
该分量与舰机相对位置无关,可通过有限带宽白噪声信号输出到式(2)描述的空间频谱来模拟其速度分量[12]:
(2)
1.2舰艉流稳态分量
特点是在垂直方向上一种特有的雄鸡尾形状的风,又称为“雄鸡尾流”,是舰艉大气扰动的主要组成部分。它的其风向与距舰艉的距离有关,临近舰艉处是向下的有效风,并且它随离开舰艉的距离增加而减弱并最终变为向上的风。若已知甲板风大小以及舰载机的近舰速度,则舰载机受到的雄鸡尾流可用与时间相关的确定性函数来模拟。
1.3舰艉流周期性分量
该分量由航母的垂荡运动和纵摇运动产生,大小与航母的不规则运动、海面风及舰载机距航母的距离有关:
(3)
式中:ωp为舰纵摇频率,rad/s;θs为舰纵摇幅度,rad,P为随机相位,rad;X为舰载机距航母纵摇中心的距离,m;u0为舰载机基准进场速度,m/s。
1.4舰艉流随机分量
可根据图1(a)仿真该分量,其中:σ(X)、τ(X)分别是与X和vw/d有关的均方根和时间常数,具体关系如图1(b)所示。

图1 舰艉流随机分量模型Fig.1 Details on the random component of carrier air-wake model
2纵向ACLS设计基础
2.1控制系统基本组成与工作原理

2.2待优化的飞行控制系统
F/A-18A飞机的ACLS采用H-dot指令模式,其纵向控制器具有图2(b)所示的基本结构[13],控制输入为油门和升降舵,控制回路主要为APCS和高度控制,其中:高度控制回路包含内环的俯仰角速度反馈、中环高度变化率反馈和外环的高度反馈;APCS的作用是稳定进场舰载机的速度和迎角,增强垂向飞行轨迹控制能力[3],简化后的控制律为:
(4)
式中:Δv、Δα、Δq、Δθ、Δh、Δnz、Δγ分别为舰载机速度、迎角、俯仰角速度、俯仰角、高度、法向过载以及航迹角相对平衡点的扰动量;Δδp为有效油门开度。
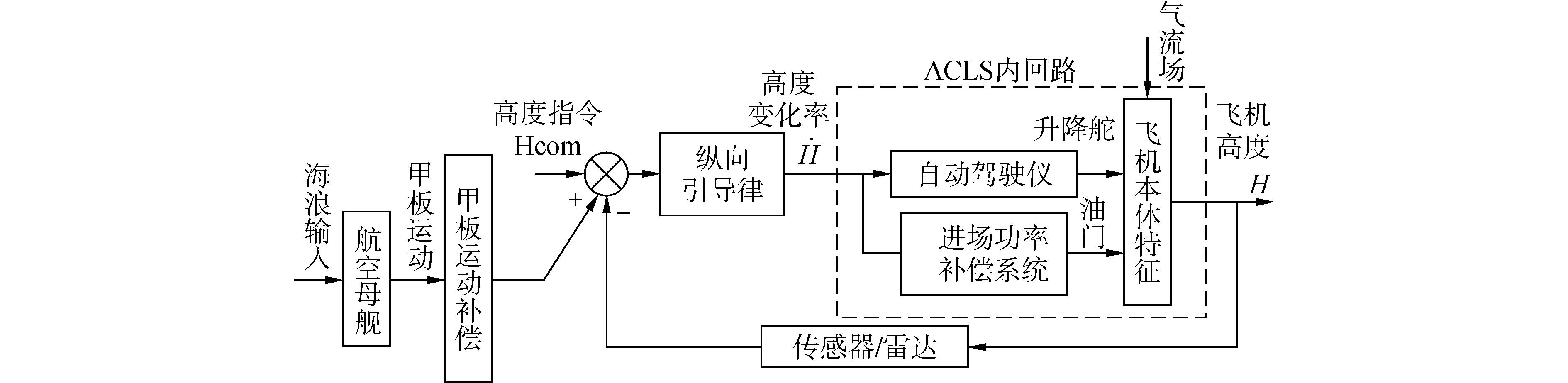
(a)原理图

(b)F/A-18A飞机的ACLS纵向基本结构图2 基于H-dot指令构型的纵向ACLSFig.2 Longitudinal channal of H-dot ACLS
本文针对图2(b)所示控制器结构完成优化设计,被控舰载机型与文献[13]中一致,舰载机进场动力学特性可由式(5)和式(6)代表的小扰动线性模型描述:
(5)
(6)
式中:Δδe、Δδc、Δδpl分别为升降舵指令、鸭翼指令、油门杆指令相对基准值的偏差;u0为基准进场速度,取70 m/s;u与w分别为气流扰动的水平纵向速度分量和垂直速度分量;g为重力加速度[13]。
本文在优化飞行控制律设计过程中将APCS参数固定为文献[13]的整定结果:K1=4、K2=-95、K3=40、K4=150、K5=20。根据图2(b)所示的ACLS纵向结构,将高度控制回路中的参数Kω取为定值12.606;8个待定参数分别是:内环滞后超前环节T1、T2,反馈增益Kq,内环前向通道比例、积分增益Kp和Ki,航迹角反馈增益Kγ、过载反馈增益Knz以及导引律中Kh(注:仿真时图2(b)中反馈的飞机角度、角速度状态量采用弧度单位制)。
2.3 性能评价方法
为保证舰载机动态调整过程的快速性和安全性,并使ACLS具有较强鲁棒性,评价依据包括纵向ACLS阶跃响应性能,以及扰流作用下舰载机高度偏差、迎角偏差、俯仰角及俯仰速率偏差等指标。此外,还要满足ACLS频域设计边界,这是确保控制算法与各硬件设备特性、与甲板运动补偿算法等其他辅助环节具有更好适配性的客观要求。图3给出ACLS设计的频域特性要求[5],测出的舰载机频域特性曲线应位于图中黑实线所界定的区域内。

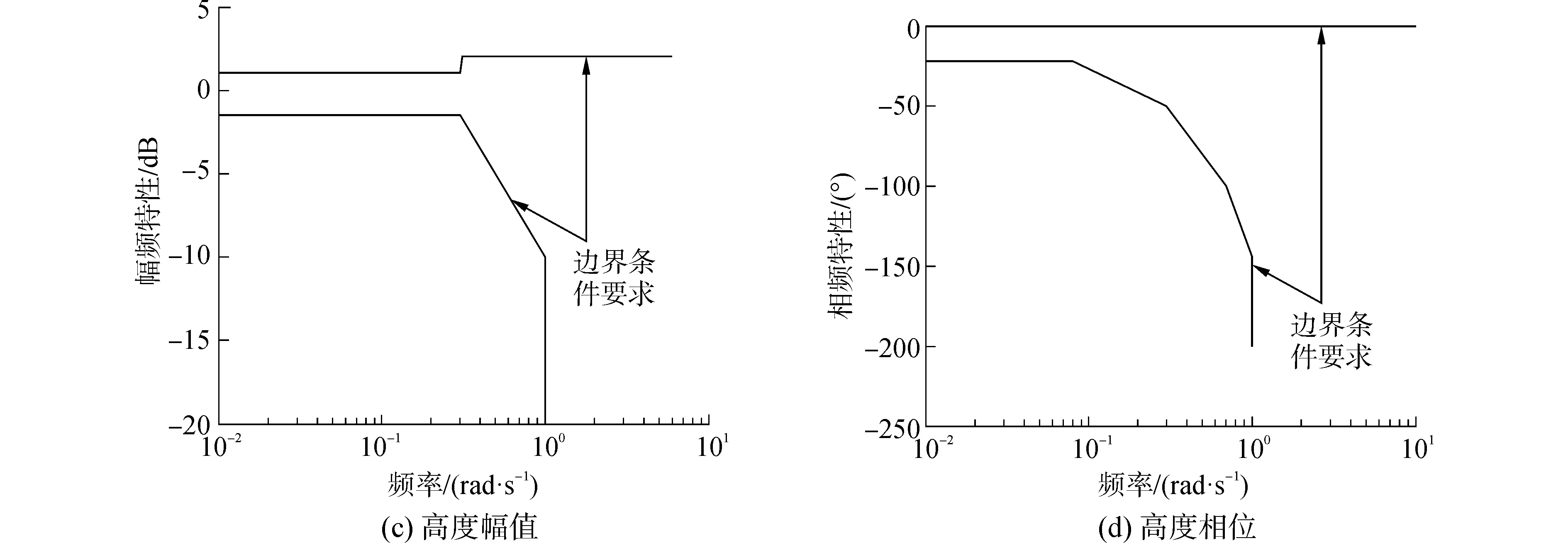
图3 ACLS频域特性边界条件要求Fig.3 Requirements on ACLS response boundary in frequency domain
本文将该边界作为算例机型ACLS参数寻优的频域评价指标,在寻优过程中也综合考虑了系统的时域性能指标。若仅考虑纵向ACLS对指令输入的响应指标,仿照F/A-18A飞机ACLS的设计性能,则一组可行的控制器参数如下[14]:
T1=0.76Ki=30.25Kq=0.6281Kγ=1
T2=0.65Kp=30.25Knz=5.729Kh=0.42
本文将其作为优化前的纵向ACLS参数。
3纵向ACLS优化设计
本文通过结合控制器参数优化和补偿控制指令来增强ACLS对抗大气扰动的能力。这是因为,在舰艉流的4大分量中,稳态分量与其它3种的特性不同:稳态分量波形具有确定性,可根据经验对其影响进行预先补偿;其余分量都具有随机性(周期性分量的相位是随机的),通过经验补偿的方法实现扰动抑制往往效果不佳,可以考虑优化控制器参数来提高系统鲁棒性。参数寻优方案是:首先,按照时域误差最小原则进行初步寻优;然后,检验寻优后系统的频域特性;最后,通过多次调整评价指标对不满足约束的部分再次寻优,以达到预期性能要求。
3.1基于遗传算法的纵向ACLS参数寻优方法
图4给出了根据遗传算法优化控制器参数的流程。将待寻优的8个参数映射成遗传个体,计算个体适应度前,需先将个体解码出对应的控制器参数代入纵向ACLS仿真进行系统仿真。由于优化期望是使ACLS在对抗扰流时的多次平均误差最小,因此本文针对每一组控制器参数进行20次仿真,每次对应的流场数据不同(可在建模舰艉流时指定不同的随机数种子或者随机相位来实现),然后计算系统状态偏差的均方根(Root Mean Square,RMS)作为最终的个体适应度值。
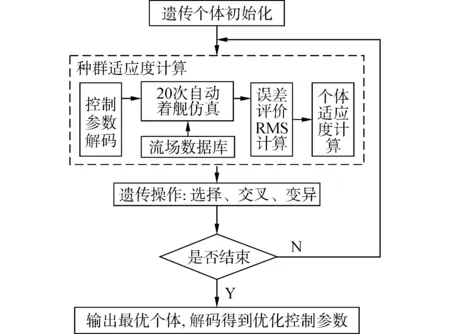
图4 遗传寻优流程图Fig.4 Flow chart of parameter optimization with genetic algorithm
3.2基于遗传算法的控制器参数时域寻优
3.2.1编码方式
在2.1节已给出了待寻优的系统参数:T1、T2、Kq、Kp、Ki、Knz、Kγ、Kh。参数编码前必须指定其取值范围,一般可根据参数的物理意义及系统调试过程的经验。本文根据文献[13]中的参数确定方法,选取参数变化范围如表1所示。
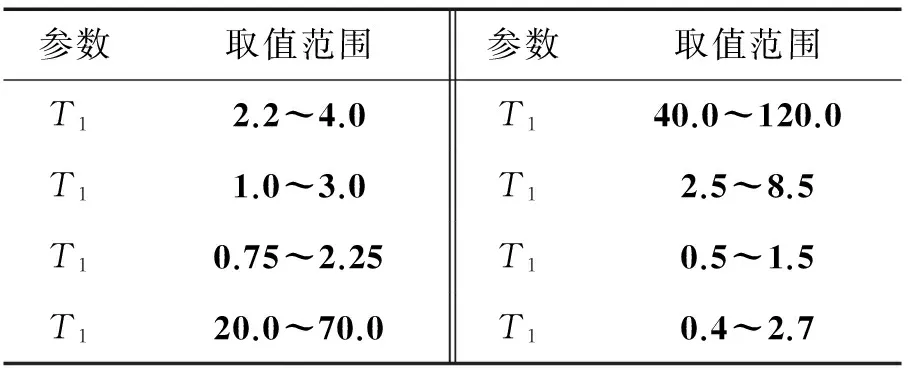
表1 控制器参数范围
对这8个参数进行2进制编码,每个参数占用16位2进制码,如图5所示,这是为保证寻优时具有足够的搜索精度,以参数T1为例,其搜索时对应的最小分辨率为(4.0-2.2)/216。

图5个体基因编码形式
Fig.5Form of encoded individual gene
3.2.2个体评价函数
仅考虑纵向ACLS的时域性能设计个体评价函数(即适应度函数),式(7)给出评价函数fitness:
(7)

3.2.3时域寻优结果
定义遗传算法参数为:交叉概率0.8,变异概率0.15,种群大小150,最大遗传代数400。在控制系统参数寻优和验证过程中所加入的扰流只含除舰艉流稳态分量之外的其余3种分量;关于稳态分量的抑制方法将在4.4节讨论。经遗传寻优后各参数取值如下:
T1=2.87Ki=70.39Kq=0.99Kγ=1
T2=1.12Kp=53.25Knz=2.59Kh=0.42
图6为纵向ACLS在时域寻优前、后对高度偏差阶跃指令响应的对比结果,显然,系统超调量和调节时间均有显著改善。图7给出寻优前、后的纵向ACLS在20次扰流作用下的偏差曲线,可见迎角和高度偏差均有显著降低,说明控制系统经寻优后鲁棒性更强。
此外,本文寻优指标(见式(7))中还体现了俯仰角、俯仰角速度等量的寻优,限于篇幅,图7未给出全部曲线对比。最优解变化曲线如图8所示,算法开始时收敛速度较快,至100代时已获得较好的结果,100~400代的适应度值趋于稳定,这说明利用遗传算法对纵向ACLS进行参数寻优是可行的。
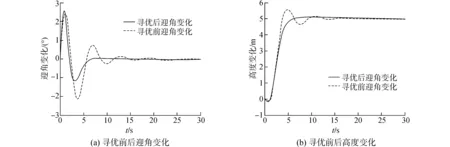
图6 纵向ACLS寻优前后阶跃响应仿真结果Fig.6 Comparison of longitudinal ACLS step responses before and after time domain parameter optimization
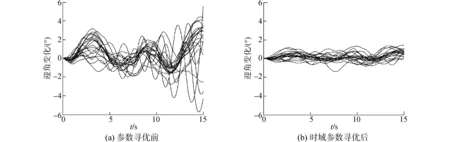
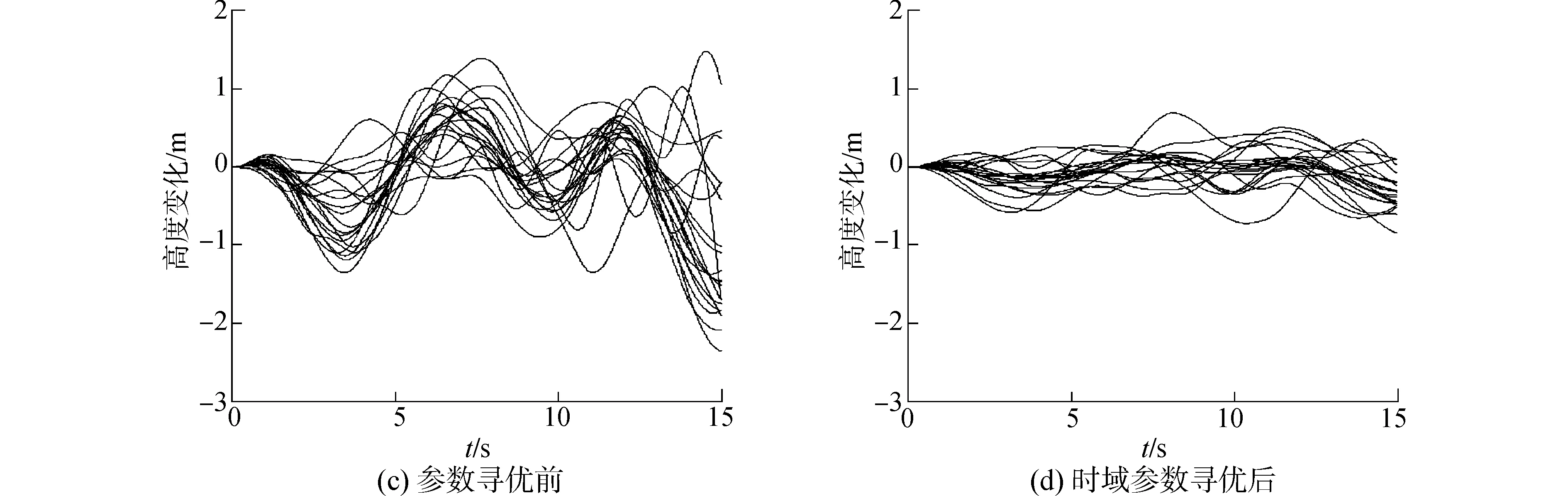
图7 加入舰艉流三种分量后的20次仿真结果Fig.7 Twenty times simulated results of longitudinal ACLS affected by three kinds of random components in burble
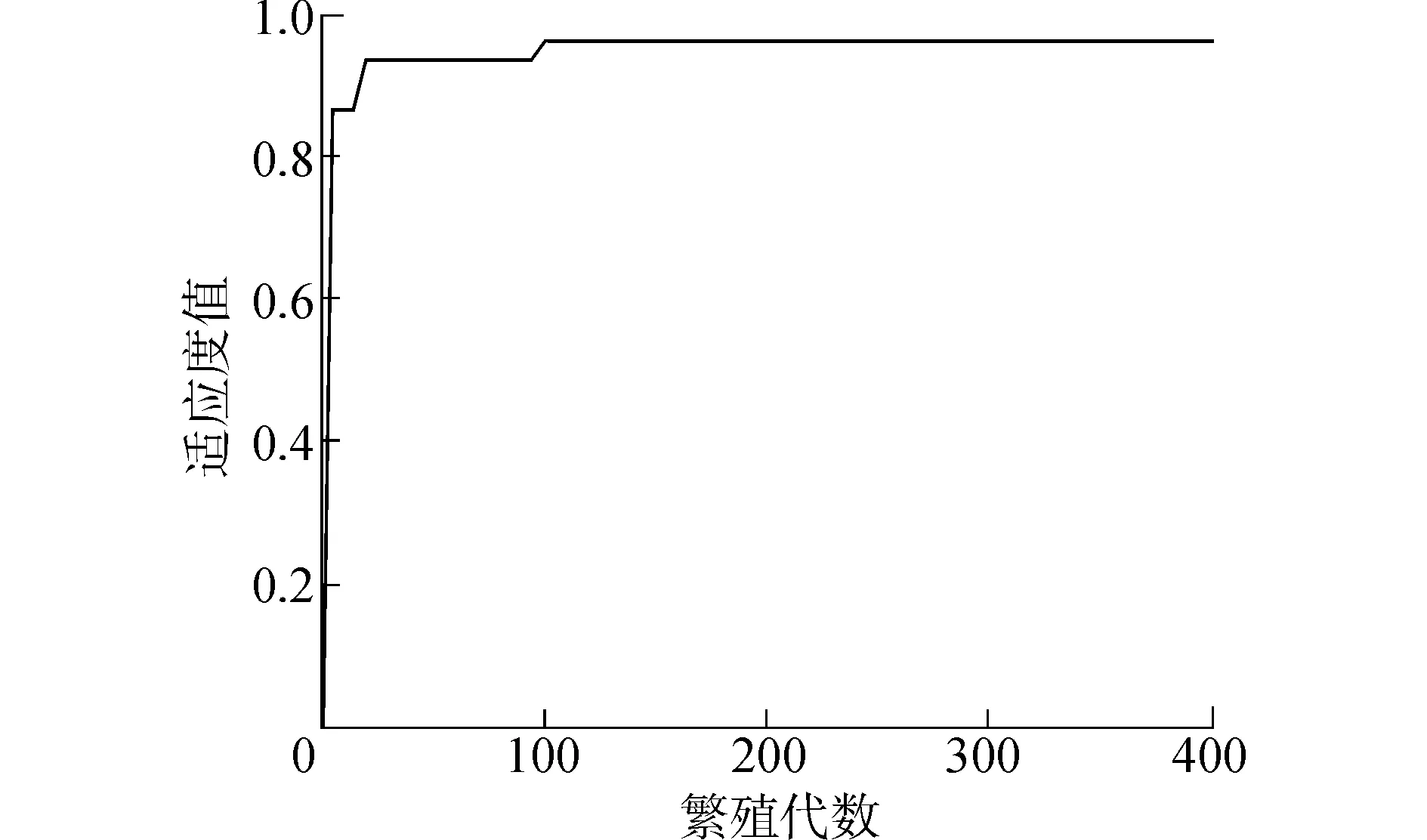
图8 最优解收敛曲线Fig.8 Convergence curve for the optimal solution
3.3控制器参数的时频域综合寻优
3.3.1时域寻优结果的频域检验
根据2.3节给出的ACLS频域安全边界,检验时域寻优后的纵向ACLS的频域性能,结果如图9所示。显然,对于垂直速度响应,系统幅、相曲线均满足边界要求;对于高度响应,系统幅频特性曲线满足边界要求,但相频特性曲线在0.5~1rad/sec的相位滞后明显超出边界限制,而该频段恰处于甲板运动的主频范围[16],此处滞后过大会导致飞机跟踪甲板运动时间滞后较大,增加甲板运动补偿难度。因此,若不对寻优过程进行调整,使系统在达到时域指标的同时也满足频域边界规定,则会影响ACLS的总体安全性。
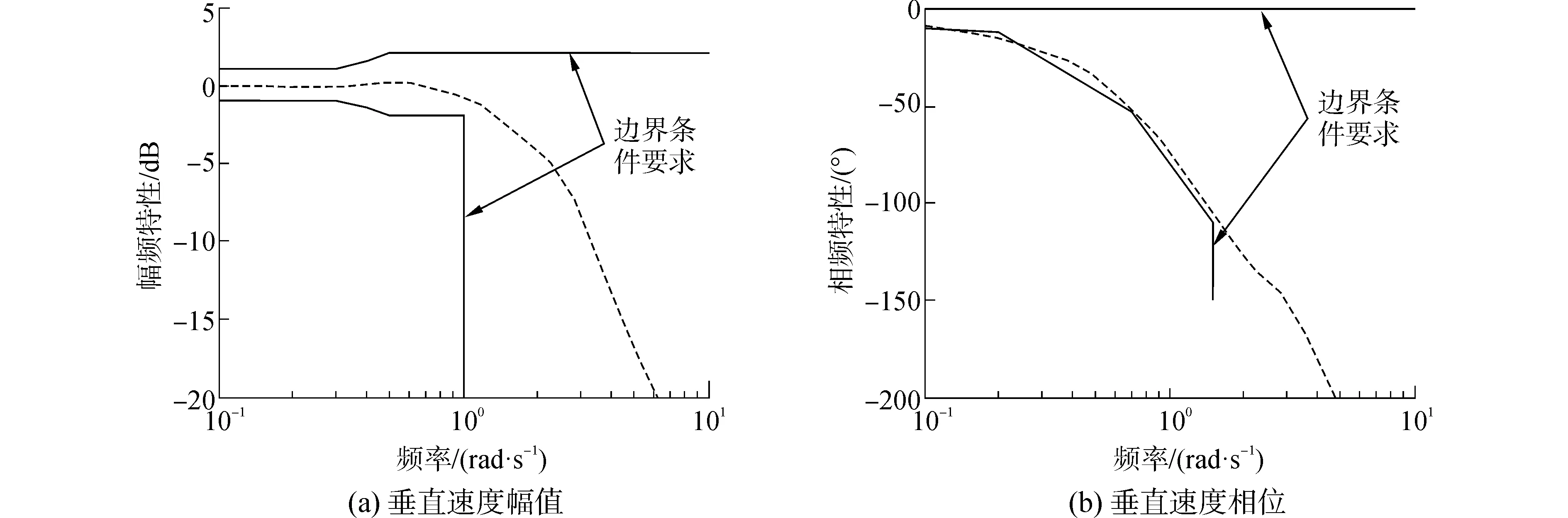
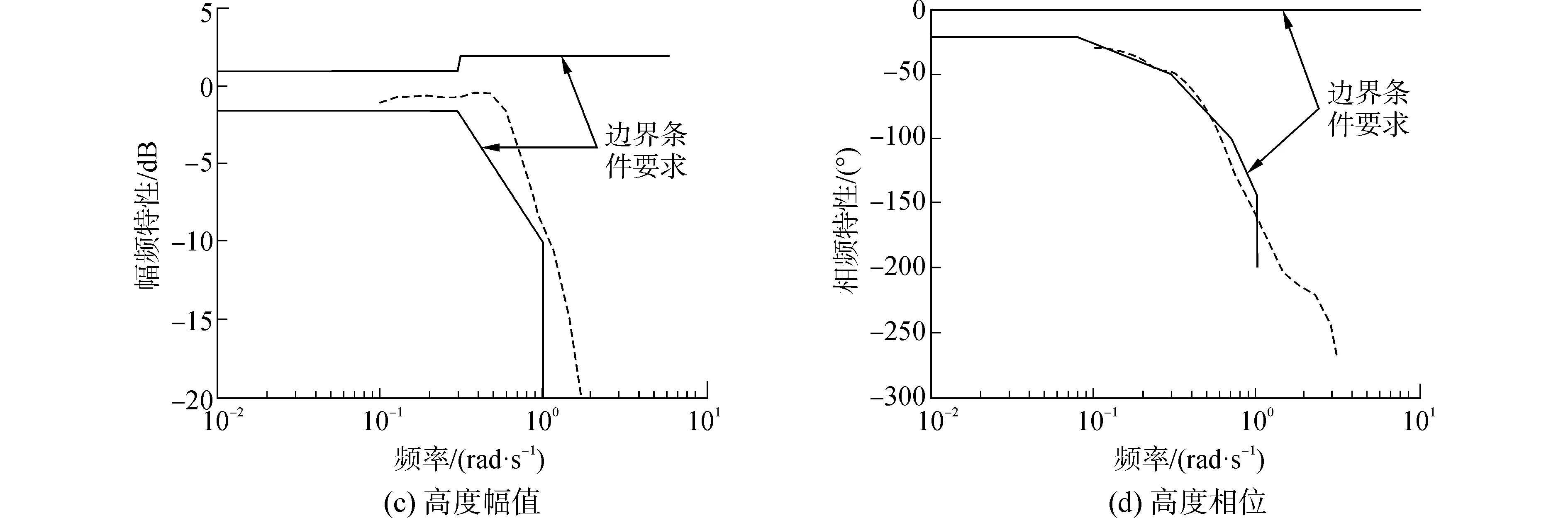
图9 时域寻优后ACLS频域响应曲线Fig.9 Frequency-domain characteristics of longitudinal ACLS after optimizing the parameters in time domain
3.3.2 时频域综合寻优
针对当前系统相频特性超限问题,重新修正评价函数fit2,修正后为:
(8)
式中:fω为系统在1rad/sec正弦信号激励下相位滞后的绝对值;wω为该指标对应权重(取0.12),函数中其余分量含义和对应权重均与式(7)一致。
利用该适应度函数,重新对参数进行遗传寻优的结果为
T1=3.98Ki=72.76Kq=1.45Kγ=1
T2=1.25Kp=39.45Knz=3.09Kh=0.42
经时频域综合寻优后的系统频域特性如图10所示。表2给出未寻优、时域寻优、时频域综合寻优3种情况下的ACLS适应度值、在舰艉流随机性分量作用下的高度偏差响应均方根(HRMS),以及在1rad/sec处的相位滞后量。

表2 不同寻优方式的结果比较

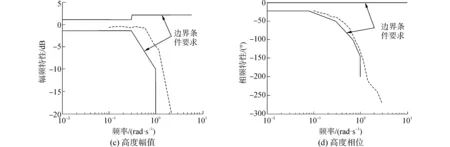
图10 时频域综合寻优后ACLS频域响应曲线Fig.10 Frequency-domain characteristics of longitudinal ACLS after optimizing the parameters in time and frequency domains
由图10及表2可知,引入时频域约束条件寻优后,ACLS的频域特性曲线已完全满足边界要求,与仅采用时域寻优的结果相比,该系统的时域偏差指标虽然略有下降(因为适应度有所降低),但与未寻优前相比,高度偏差仍有明显改善。
3.4 舰艉流稳态分量的抑制方法
舰艉流稳态分量具有确定性,可根据经验对其干扰进行预先补偿,为分析稳态分量对着舰性能的影响,将完整的舰艉流4个分量加入经参数寻优前、后的ACLS,多次仿真后分别得到高度偏差曲线图11(a)和图11(b)。可见,高度偏差曲线集出现明显的先向上波动、再向下波动,这是进场舰载机进入尾流区时先遭遇明显的上洗流、后遭遇下洗流造成的[15]。针对这种情况,文献[15]中指出:可在以俯仰姿态为基准的飞行控制系统的反馈指令上叠加俯仰指令前馈信号,以削弱由舰艉流稳态分量引起的航迹偏差。仿照该思路,本文尝试在高度变化率回路中预先叠加附加指令来抑制稳态分量的影响,如图12(a)所示;并且,采取分段补偿策略,补偿值切换两次,详细设计补偿引入的时刻和大小,以确保补偿后的系统响应指标最优。
为此,本文仍采用遗传算法技术,对补偿时刻及补偿幅度进行编码,将前文时频域综合寻优后的参数固定后单独对该补偿指令的波形寻优,适应度函数仍根据式(8),最后得到的补偿指令波形如图12(b)所示。

图11 ACLS对完整舰艉气流扰动的响应Fig.11 Responses of ACLS to full ship burble
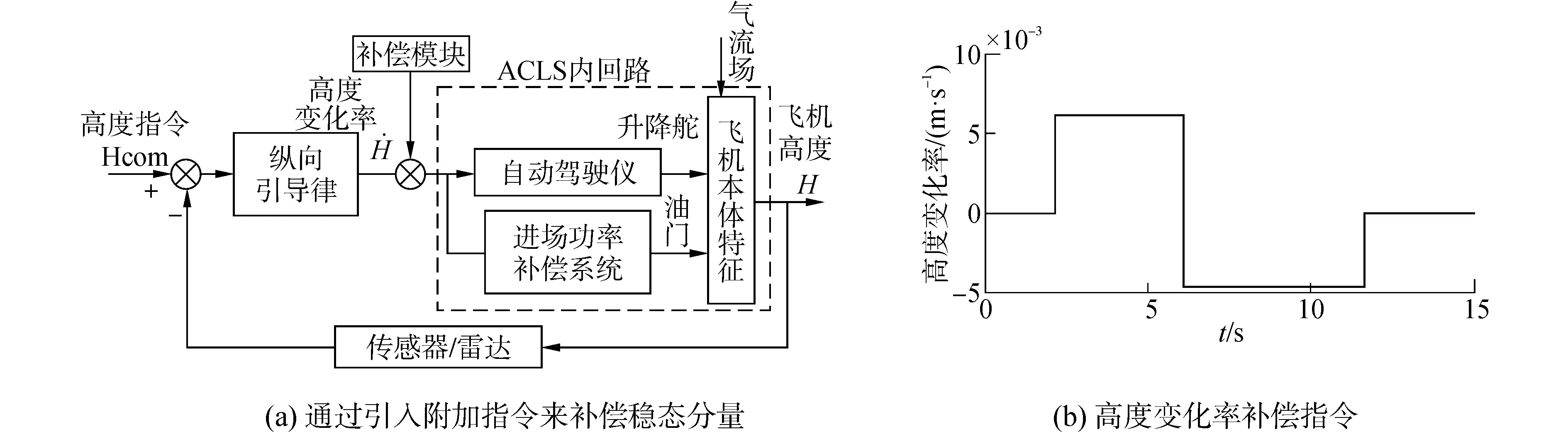
图12 针对舰艉流稳态分量的指令补偿Fig.12 Compensated command for the steady component of carrier air wake
加入补偿指令后,纵向ACLS对抗20次完整舰艉流的仿真结果如图11(c)所示,并且计算可知:仅考虑时、频域参数寻优的ACLS的HRMS为0.467 3 m,而综合指令补偿和参数寻优的ACLS的HRMS为0.351 7 m,这说明高度变化率指令补偿对于改善纵向ACLS抑制稳态上、下洗流的影响有积极作用。
4纵向ACLS优化设计验证
前文已实现了基于完整舰艉流分量的扰流最优抑制。通过完成控制参数寻优以抑制3种随机分量与完成补偿指令寻优以抑制稳态分量相结合,使所设计的纵向ACLS在舰艉流作用下具有较高的时域控制精度,并且满足频域安全边界约束。为进一步表明优化后的纵向ACLS对扰流具有更强的抑制能力,对纵向ACLS响应100组完整舰艉流的情况进行仿真,仍得到较好的偏差统计结果见表3。
表3进场舰载机高度偏差响应统计结果
Table 3Statistics of altitude deviation of the carrier-based aircraft in approach phase m

优化方式平均偏差值最大绝对峰值偏差平均绝对峰值偏差优化前-0.19971.58050.8246参数寻优-0.13340.94930.6301参数寻优和指令补偿-0.12490.75050.5703
最后,对优化后的纵向ACLS进行综合路径跟踪性能测试,仿真初始条件设为:进场舰载机存在初始高度偏差,在着舰前35 s时加入幅值5 m的高度纠偏指令,在着舰前15 s时加入舰艉流扰动。对比纵向ACLS在优化设计前、后的高度偏差响应,如图13所示。由此可知:尽管两个着舰控制系统都能有效引导舰载机着舰,使舰载机通过前期调整快速消除高度偏差,进入平稳飞行状态,但显然优化设计后的ACLS调节时间更短,超调更小。
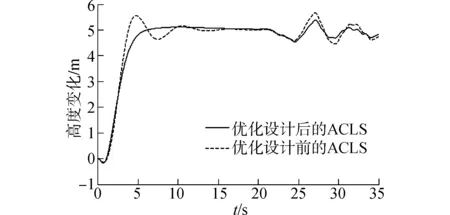
图13 舰载机高度偏差对比Fig.13 Comparison of carrier-based aircraft altitude deviations
5结论
论文针对ACLS优化舰艉流抑制能力进行设计,分别研究了随机性扰和稳态扰流分量的抑制和补偿方法,得到结论如下:
1)扰流抑制可分类处理,对于固定规律的稳态分量可采用指令补偿的方式进行抑制,其余分量需采用控制器参数优化设计的方式进行抑制;
2)控制器参数寻优要同时兼顾时域误差最小和频域边界约束,才能获得更好的综合效果,并能与甲板运动补偿环节更好适配;
3)将参数的时、频域综合寻优策略和稳态扰流抑制的内环指令补偿叠加使用,可在完整扰流作用下实现很好的控制效果。
参考文献:
[1]STEINBERG M. A fuzzy logic based f/a-18 automatic carrier landing system[C]//Navigation and control conference, AIAA. Washington, D.C., 1992: 407-417.
[2]HESS R K, URNES J M, MOOMAW R F, et al. H-dot automatic carrier landing system for approach control in turbulence[J]. Journal of guidance, control, and dynamics, 1981, 4(2): 177-183.
[3]HUFF R K, KESSLER G K. Enhanced display, flight controls and guidance systems for approach and landing[R]. Patuxent River, MD: Naval Air Test Center Report, 1991.
[4]URNES J M, HESS R K. Development of the F/A-18A automatic carrier landing system[J]. Journal of guidance, control, and dynamics, 1985, 8(3): 289-295.
[5]PRICKETT A L, PARKES C J. Flight testing of the F/A-18E/F automatic carrier landing system[C]//IEEE Proceedings aerospace conference. Big Sky, MT, 2001: 52606-52611.
[6]吉祥. 舰载机自动着舰轨迹控制技术研究[D]. 南京: 南京航空航天大学, 2011: 49-58.
JI Xiang. The research on trajectory control of automatic carrier landing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011: 49-58.
[7]满翠芳, 江驹, 王新华, 等. 舰载机动力补偿系统模糊逻辑设计技术[J]. 南京航空航天大学学报, 2010, 42(5): 656-660. MAN Cuifang, JIANG Ju, WANG Xinhua, et al. Carrier-based aircraft approach power compensator system design based on fuzzy logic techniques[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2010, 42(5): 656-660.
[8]李冀北, 侯志强. 自动着舰导引律设计及其参数优化[C]//第20届中国控制与决策会议. [S.l.], 2008.
[9]焦鑫, 江驹, 王新华, 等. 基于模型参考模糊自适应的舰尾流抑制方法[J]. 南京航空航天大学学报, 2013, 45(3): 396-401.
JIAO Xin, JIANG Ju, WANG Xinhua, et al. Air wake rejecting method based on model reference fuzzy adapting system control[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2013, 45(3): 396-401.
[10]朱齐丹, 孟雪, 张智. 基于非线性动态逆滑模的纵向着舰系统设计[J]. 系统工程与电子技术, 2014, 36(10): 2037-2042.
ZHU Qidan, MENG Xue, ZHANG Zhi. Design of Longitudinal carrier landing system using nonlinear dynamic inversion and sliding mode control[J]. Systems engineering and electronics, 2014, 36(10): 2037-2042.
[11]SUBRAHMANYAM M B. H-infinity design of F/A-18A automatic carrier landing system[J]. Journal of guidance, control, and dynamics, 1994, 17(1): 187-191.
[12]Department of Defense Interface Standard. Flying qualities of piloted aircraft, MIL-HDBK-1797[S]. USA: Department of Defense, 1997: 686-689.
[13]董然. ACLS纵向内回路控制系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 34-55.
DONG Ran. Research on the longitudinal inner loop configuration in ACLS[D]. Harbin: Harbin Engineering University, 2013: 34-55.
[14]邱兵. 舰载机自动着舰模糊控制系统设计[D]. 哈尔滨: 哈尔滨工程大学, 2014: 21-31.
QIU Bing. The design of fuzzy control system for aircraft automation carrier landing[D]. Harbin: Harbin Engineering University, 2014: 21-31.
[15]RUDOWSKY T, COOK S, HYNES M, et al. Review of the carrier approach criteria for carrier-based aircraft[R]. NAW-CADPAX/ TR-2002/71. [S.l.]: Naval Air Warfare Center Aircraft Division, 2002.
[16]SIDAR M M, DOOLIN B F. On the feasibility of real-time prediction of aircraft carrier motion at sea[J]. IEEE transactions on automatic control, 1983, 28(3): 350-356.
本文引用格式:
张智, 李佳桐, 董然,等. 纵向ACLS对舰艉流抑制的优化设计[J]. 哈尔滨工程大学学报, 2016, 37(6): 802-811.
ZHANG Zhi,LI Jiatong,DONG Ran, et al. Optimal design of longitudinal automatic carrier landing system for carrier air wake rejection[J]. Journal of Harbin Engineering University, 2016, 37(6): 802-811.
收稿日期:2015-04-28.
基金项目:国家自然科学基金项目(61104037, 61304060);国家国际科技合作专项(2013DFR10030);中央高校基本科研业务费(HEUCFX41304).
作者简介:张智(1981-), 男, 副教授; 通信作者:李佳桐,E-mail:S313040175_ljt@hrbeu.edu.cn.
DOI:10.11990/jheu.201504065
中图分类号:TP273,V212
文献标志码:A
文章编号:1006-7043(2016)06-0802-10
Optimal design of longitudinal automatic carrier landing system for carrier air wake rejection
ZHANG Zhi,LI Jiatong,DONG Ran,YUAN Xin
(College of Automation,Harbin Engineering University,Harbin 150001,China)
Abstract:Carrier air wake disturbance is one of the main factors contributing to carrier-based aircraft landing errors. As such, a powerful automatic carrier landing system must have a strong capacity to reject airflow. In this study, we examine the basic configuration of an automatic carrier landing system (ACLS) controller employed by USA F/A-18A fighter jets and design an optimal longitudinal control for use in a carrier-based aircraft model. For the random component of a carrier air wake, we use a genetic algorithm to perform an offline optimization of controller parameters considering both property indices in the time domain and security boundaries in the frequency domain. For the steady component of the carrier air wake, the formerly optimized parameters have been fixed , and we add a compensation command to the controller's inner loop to achieve an optimal suppression of full carrier air wake . We then verify the optimized flight control system through simulation. The results show that the proposed optimization scheme is feasible and effective. The optimized ACLS demonstrates better command response characteristics and robustness compared with the original system, thereby improving the landing accuracy of aircraft.
Keywords:carrier-based aircraft; carrier air wake; automatic carrier landing system(ACLS); genetic algorithm; security boundaries in frequency domain; compensation command
网络出版日期:2016-04-21.
李佳桐(1990-), 女, 硕士研究生.

