敷设气囊的充水圆柱壳的声辐射特性*

段嘉希，周其斗，郑　晗

(海军工程大学 舰船工程系， 湖北 武汉　430033)



敷设气囊的充水圆柱壳的声辐射特性*

段嘉希，周其斗，郑晗

(海军工程大学 舰船工程系， 湖北 武汉430033)

摘要：为降低充水圆柱壳受内部点声源激励时的水下辐射噪声，在其外壳上敷设气囊，形成气囊圆柱壳。为指导气囊圆柱壳的设计，将充水裸圆柱壳和充水气囊圆柱壳分别简化为单、双层无限长隔板。比较隔板、气体与水的波阻抗，分析气体声速与层厚对双层无限长隔板在平面声波入射时的低频声辐射的影响机理。分析表明，声速小的气体和适当的气层厚度可以降低双层障板的辐射噪声。采用声无限元法计算气囊圆柱壳的水下声辐射，结论与对隔板的机理分析吻合。优化设计出的充水CO2气囊圆柱壳的水下辐射声功率与远场辐射声压明显低于充水裸圆柱壳。

关键词：气囊圆柱壳；隔板；辐射声功率；声速；无限元法

声学覆盖层是常用的降低水下航行体振动与辐射噪声的设备，通常由多层功能各异的复合材料[1-2]制成，对覆盖层降低结构声辐射性能的研究始于层合板，Kerwin[3]对由“基结构-黏弹性层-约束层”组成的层合板的弯曲特性进行了理论与研究，提出了复剪切模量的概念。实验表明，对约束层厚度远小于基结构厚度且复剪切模量的虚部远小于实部的层合结构，可采用该理论分析其弯曲特性。Berry等[4]将该成果拓展到了有限结构，对浸在重质流体中，四周简支的覆盖解耦材料的弯曲平板的动力学与声学响应进行了理论研究。Lu等[5]基于有限元法，采用NASTRAN直接频率响应分析求解序列，对层合板的振动进行了数值分析，结果与实验值吻合良好。

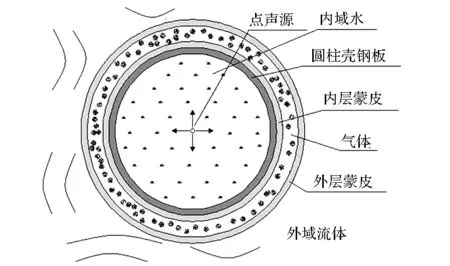
图1　敷设气囊的充水圆柱壳Fig.1　Gas-bag coated water-filled cylindrical shell

圆柱壳是水下航行回转体的基本结构形式。一些学者分析了敷设阻尼层的圆柱壳的振动与声辐射特性。姚熊亮等[6]采用实验法研究了去耦瓦的敷设方式对双层圆柱壳的水下振动与声辐射的影响，其白噪声激励工况表明，在外壳上全部敷设去耦瓦可有效控制双层圆柱壳的总辐射声压，但未对其进行深入的频谱分析。白振国等[7]在半径3.5 m/3 m的双层圆柱壳上敷设了多层隔声阻尼层，对降低高频噪声有明显的效果，但在500 Hz以下频段作用不明显。Cao等[8]采用波数谱方法对敷设阻尼层的圆柱壳进行了研究，分析了辐射声压的螺旋波数谱，但其关注重点仍在高频段。本文提出一种新型的气囊式声学覆盖层，即：以充水的圆柱壳模拟水下航行回转体的非耐压舱段，在其外壳上敷设由阻尼材料制成的气囊，形成如图1所示的敷设气囊的充水圆柱壳(简称“气囊圆柱壳”)，讨论降低受点声源激励的充水圆柱壳的低频辐射噪声的可行性。其中，气囊包括内、外层蒙皮及充入的气体。分别建立气囊圆柱壳与裸充水圆柱壳(简称“裸圆柱壳”，如图2所示)的一维简化模型和三维有限元模型。对一维简化模型进行定性的机理分析和编程计算，对三维有限元模型采用声无限元法进行数值计算，分析气囊圆柱壳的降噪效果。

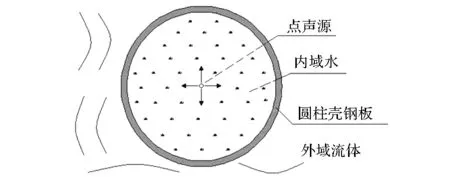
图2　裸充水圆柱壳Fig.2　Bare water-filled cylindrical shell

1隔板的声学特性

受内部点声源激励，充水圆柱壳发生弯曲振动。壳板不同部位受声波入射角度不同，其振动是由多种波长的弯曲波按照不同幅值叠加而成的。为探讨气体声速和层厚对气囊圆柱壳辐射噪声的影响，为气囊覆盖层的参数设计提供指导，将“气囊圆柱壳”和“裸圆柱壳”分别简化为一维无限长隔板，采用理论手段和MATLAB编程，对其在平面声波入射时的振动与声辐射规律进行定性的机理分析。这种简化方式忽略了圆柱壳的一些结构特性[9]，但不影响对气体参数的定性分析，且可以更直接地从气体中声波、水中声波与结构弯曲波之间的波数关系[10]揭示气体对气囊圆柱壳辐射噪声的影响机理。

1.1隔板的声传播机理分析

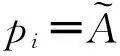
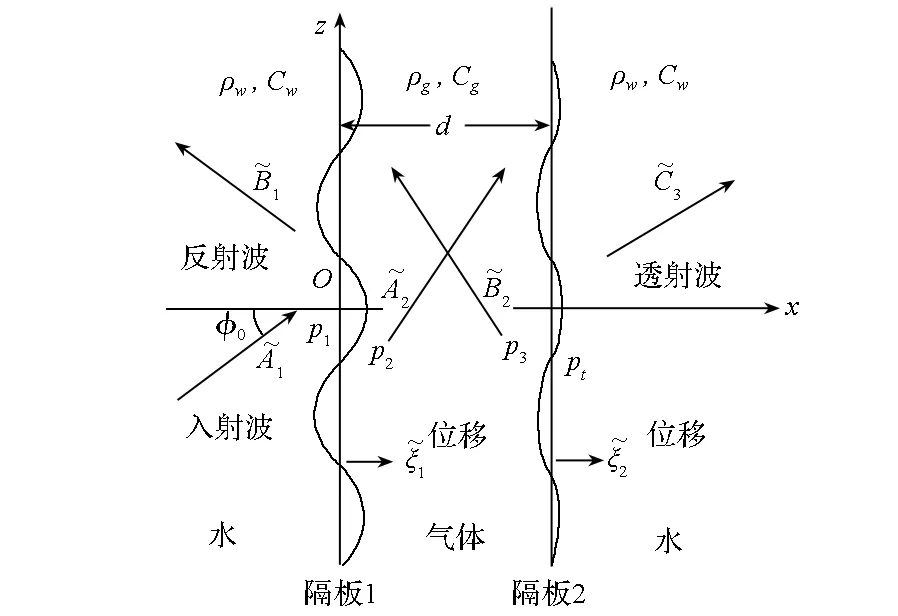
图3　双层隔板的声辐射Fig.3　Sound radiation from double-leaf partitions

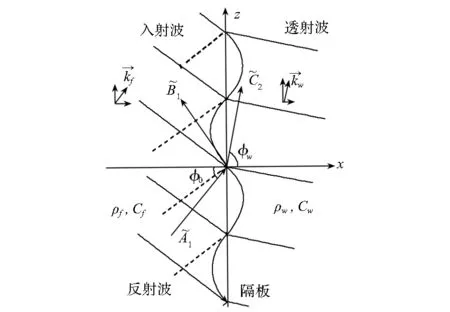
图4　单层隔板的声辐射Fig.4　Sound radiation of single-leaf partition

假设D1s，m1s，ξ1s与D1r，m1r，ξ1r分别为钢板和阻尼层的复刚度、质量和位移。分析图3中隔板1钢板的动力学特性得：

(1)

式中，-σz为橡胶对钢板施加的约束力。

分析隔板1中阻尼层的动力学特性得：

(2)其中，p1与p2分别为隔板1左右两侧的总声压。由于钢板与阻尼层贴合紧密，可认为ξ1s=ξ1r=ξ1。将式(1)与式(2)相加，引入隔板1的总复刚度D1=D1s+D1r与总质量m1=m1s+m1r，得到隔板1的动力学方程：

(3)

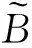
(4a)

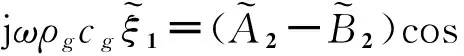
(4b)

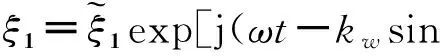
隔板1两侧的总声压p1与p2分别为：

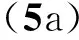
φgz)]

(5b)

其中，kwsinφ0=kgsinφg。

将式4(b)、式5(a)、式5(b)代入式(3)中，得到：

(6)

分析隔板2的振动方程：

(7)

式中，p3和pt分别为隔板2左右两侧的总声场：

exp[j(ωt-kgsinφgz)]

(8a)

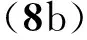
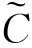
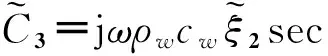
(9a)

(9b)

将式8(a)、式8(b)与式9(b)代入式(7)中，得到：

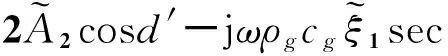
(10)

将式(4b)代入式(9b)，得到隔板1与隔板2的位移关系：

(11)

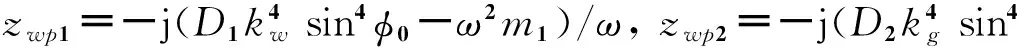
(12)

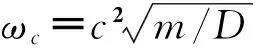
(13)

对充水的裸圆柱壳，采用同样的方法，可求得低频段单层隔板右侧的声波幅值：

(14)

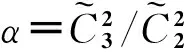
T=10 lgα

(15)

这样，T< 0时，双层隔板有降低辐射噪声的效果；T> 0时，双层隔板无效。

1.2MATLAB数值分析

采用MATLAB对式(15)编程，计算10～700 Hz频段的T值，步长2 Hz。各参数取值如下：钢板密度7850 kg/m3，板厚6.35 mm；阻尼层密度1200 kg/m3，内外阻尼层厚h1与h2；气体密度5.36 kg/m3，层厚d，声速c_gas；水密度1000 kg/m3，声速1450 m/s。

1.2.1气体声速的影响

设定c_gas分别为960 m/s，640 m/s，320 m/s，127 m/s；d=60 mm，h1=h2=10 mm；入射角度分别为0°，20°，40°。计算所得频响曲线如图5所示，表明：在平面声波从水中入射的情况下，双层隔板在10～700 Hz都有降噪效果，频率越高，降噪效果越好。入射角在0°～40°内变化时，其对双层隔板的降噪效果影响很小；气体声速越小，降噪效果越好。

1.2.2气层厚度的影响

设定声波入射角为20°；c_gas分别为127 m/s，330 m/s；d分别为40 mm，80 mm，160 mm，320 mm，640 mm；钢板厚度为12.7 mm，h1=h2=10 mm，气体密度为5.36 kg/m3。计算结果如图6所示。结果表明：气层较薄时，双层隔板的降噪效果在10～700 Hz频段变化平缓；气层变厚会导致T值在该频段出现较均匀的波峰和波谷，峰值和波谷分别出现在气层厚度为气体中声波半波长(0.5λg)的整数倍处和1/4波长(0.25λg)的奇数倍处。声速为330 m/s时，在300 Hz以下频段，适当增加气层厚度可使双层隔板降噪效果更好；但在厚度达到320 mm时，在500 Hz处出现较大峰值。声速为127 m/s时，峰值则更加密集。因此，气层厚度与气体声速之比越大，曲线中峰值越密集。图5中，由于气体层厚较小，在10～700 Hz频段各曲线均不能达到d为0.5λg的整数倍，因此未出现峰值。

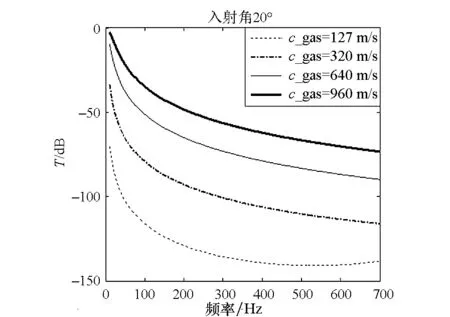
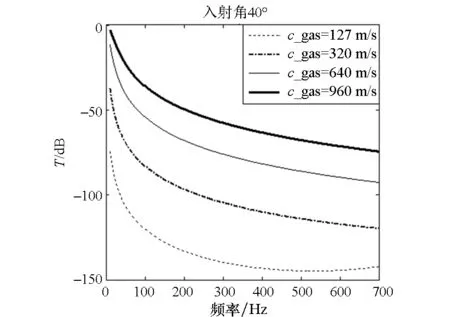
图5　气体声速及入射角对双层隔板降噪效果的影响Fig.5　Influence of sound velocities of gases and incident angles on the noise reduction effect of double-leaf partitions

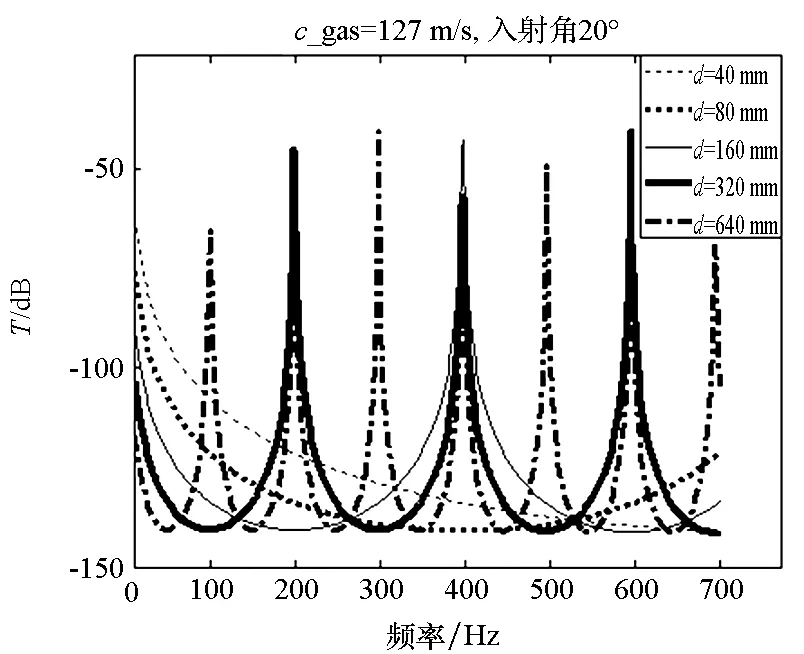
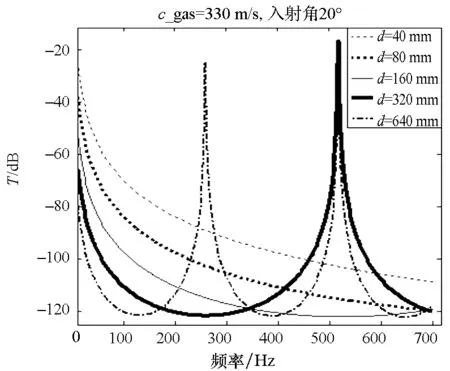
图6　气层厚度对双层隔板降噪效果的影响Fig.6　Influences of gas thickness on the noise reduction effects of double-leaf partitions

2圆柱壳有限元分析

声无限元法是由Astley等[12]提出，并经过实验和理论验证的一种可以快速计算无限域中声场的算法，在国外已得到广泛应用。本节采用声无限元法计算气囊圆柱壳和裸圆柱壳在水下受内部点声源激励时的辐射声功率级。对比1.2节和无限元的计算结果，分析气体声速和气层厚度对气囊圆柱壳辐射声功率的影响规律，得出最优方案。

2.1声无限元法

声无限元法的动力学方程由刚度矩阵和质量矩阵装配而成。无限元法在结构边界S外的无限域R设置一虚拟边界S1。声场p满足以下方程组：

(16)

其中，第一式为无限域内Helmholtz方程，式中k=ω/c为波数；第二式为虚拟边界S1上满足的纽曼边界条件，其中g相当于法向速度与阻抗的乘积[12]；第三式为无穷远处满足的索末菲条件[12]，式中r为无限元极点到声场点的距离。只需找到一个满足方程组(16)的解p，即可求得外域声场问题。引入一测试函数u，可以得到：

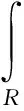
(17)

对虚拟边界S1内、外的流体介质分别进行有限元离散与无限元离散，可得到由有限元刚度矩阵和无限元刚度矩阵装配成的总刚度矩阵和由有限元质量矩阵和无限元质量矩阵装配成的总质量矩阵，进而求解出整个外域声场问题[13]。

2.2气体参数的有限元/无限元分析

图7为充水圆柱壳在水中受内部点声源激励的示意图。充水裸圆柱壳与充水气囊圆柱壳均处于无限水域中，并在各自结构外设定如⑨所示的无限元面。图中，①～⑩分别为：钢壳板厚，内、外域水，端盖厚度，点声源位置，柱壳直径，内层蒙皮厚度，气层厚度，外层蒙皮厚度，无限元面和柱壳长度。借助NASTRAN无限元技术，将图7中⑨采用声无限单元CACINF进行网格划分，并设置径向插值阶数为7，采用RLOAD1卡片定义点声源。柱壳最大单元尺度180 mm，端盖最大单元尺度230 mm，无限元面最大单元尺度330 mm。钢板、阻尼蒙皮采用板单元建模，气体和内域水采用正六面体单元建模。由于采用无指向性的点声源激励，敷设了气囊的钢壳与未敷设气囊的端盖均受到点声源的作用。为了专门研究气囊的作用，应除去端盖的影响。在1.1节的分析中已指出，由于平板与两侧流体的耦合作用，在远低于截止频率的频段，刚度项的作用远低于惯性项的作用。因此，将端盖材料的密度设定为钢的106倍，而不改变端盖的刚度，使得端盖对声辐射的贡献可以忽略不计。如图8所示，采用板单元对圆柱壳结构进行有限元离散；采用流体有限元对圆柱壳内的水、气囊中气体及圆柱壳外无限元面内的水进行离散。计算圆柱壳湿表面的辐射声功率级，并提取远场点声压级，如图7中第二图所示。

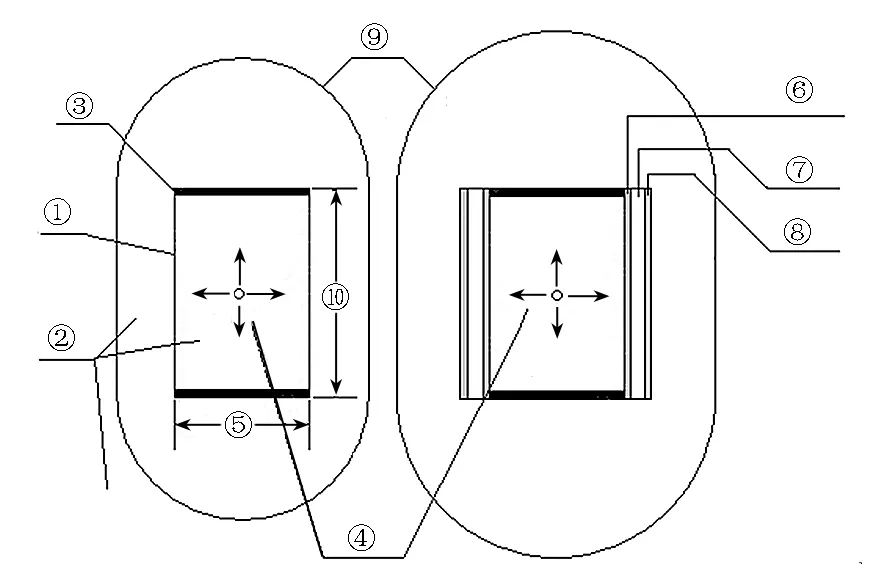
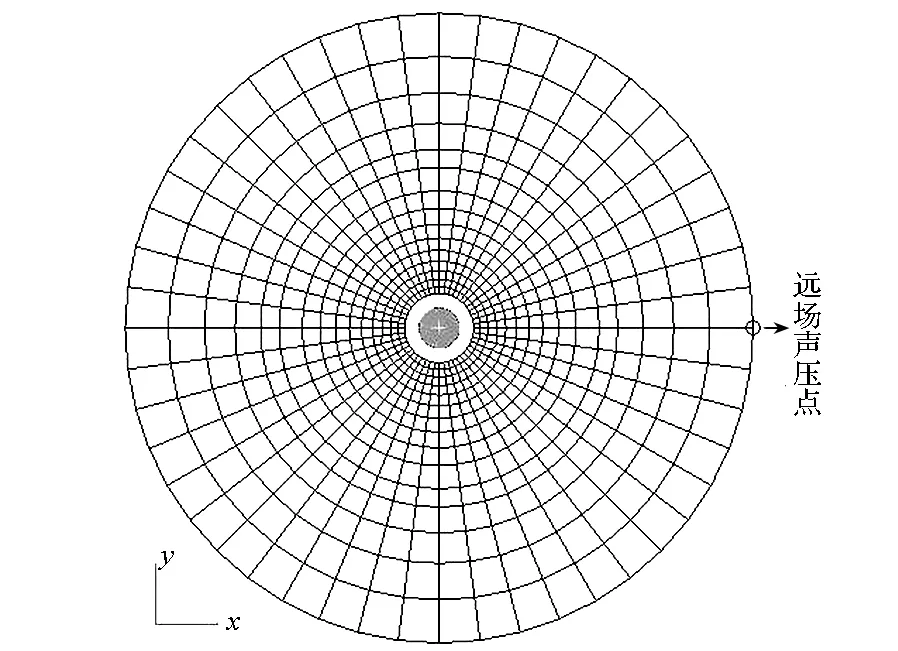
图7　水下计算工况设置Fig.7　Cases of underwater calculation

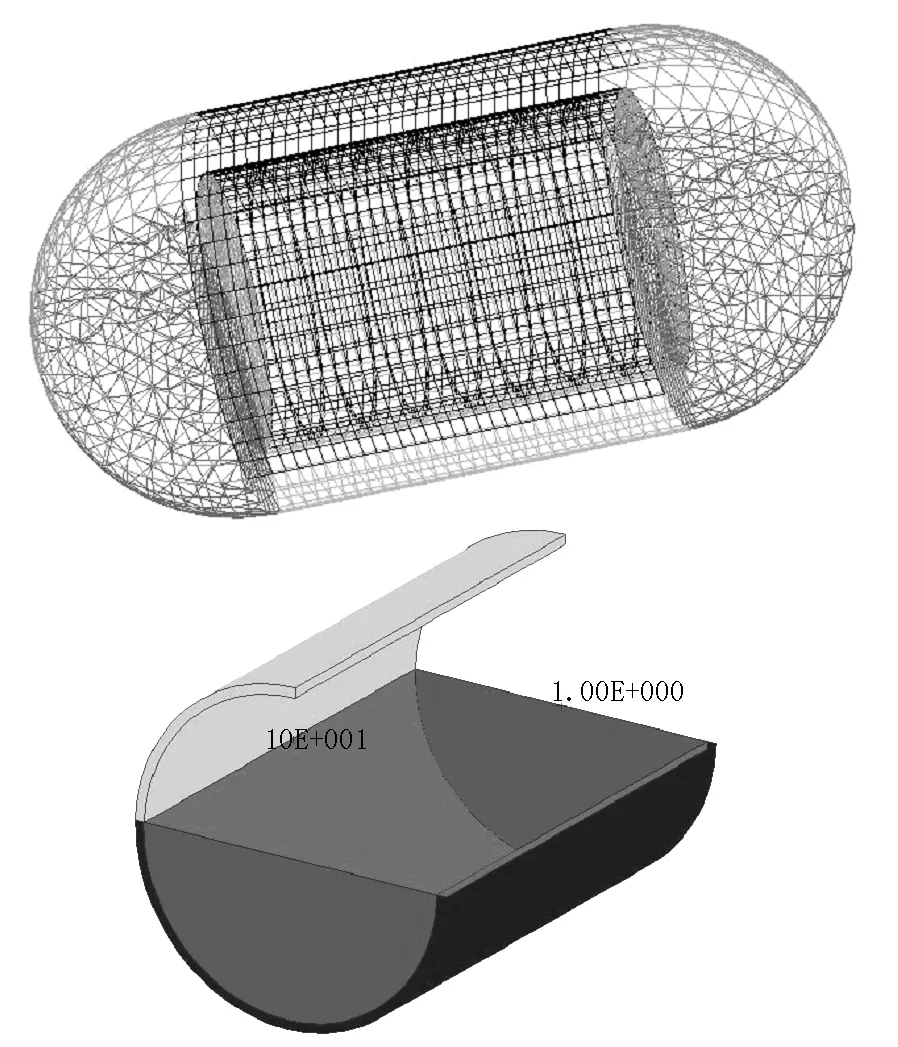
图8　有限元与无限元网格Fig.8　Finite element and infinite element meshing

2.2.1气体声速的影响

采用声无限元法分析气体声速对气囊圆柱壳降噪效果的影响。设定图7中参数①、③分别为：6.35 mm，25.4 mm；⑤～⑧分别为：1270 mm，10 mm，60 mm，10 mm；⑩为1905 mm。为便于计算，将点声源强度Q对时间t求导数，从而将激励声源设定为与频率无关的量，为1.257×107mm3/s2。气体声速分别取为960 m/s，640 m/s，320 m/s，127 m/s。计算频带为18～498 Hz，步长4 Hz。计算各气囊圆柱壳湿表面辐射声功率级与远场点声压级频响曲线，如图9所示，其中远场点距点声源10 m。结果表明，气囊圆柱壳的辐射声功率级与远场声压级的频谱规律基本一致；且气体声速越小，辐射声功率级与远场声压级越小，降噪效果越好；随着气体声速变小，其频响曲线上会出现的小的峰值，且声速越小，谱峰越多。采用声无限元法计算三维圆柱壳模型所得的规律与采用MATLAB对一维简化模型公式编程计算所得的规律符合良好，均说明：采用声速较小的气体充入气囊可以得到更好的降噪效果，但应考虑到声速越小谱峰出现越密集这一现象。

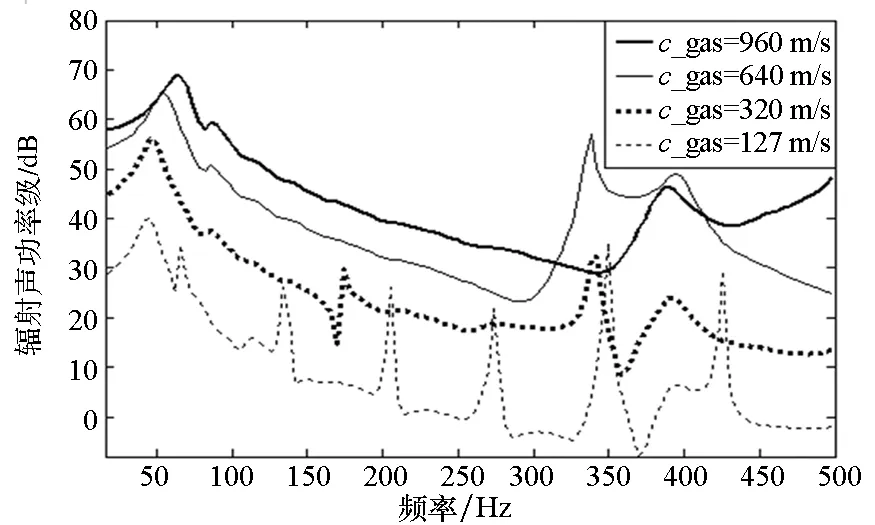
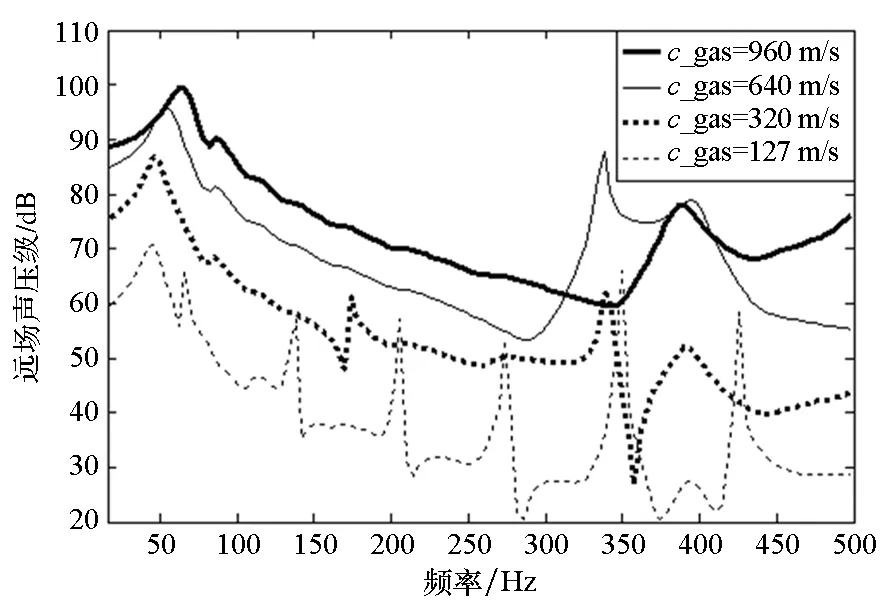
图9　充入不同声速气体的充水气囊圆柱壳辐射声功率级与远场声压级Fig.9　Radiated power and far field sound pressure level of GCWCS with gases of different sound velocities

2.2.2气层厚度的影响

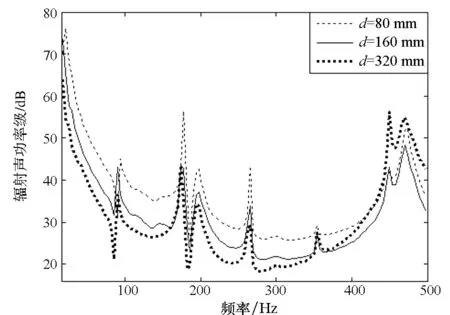
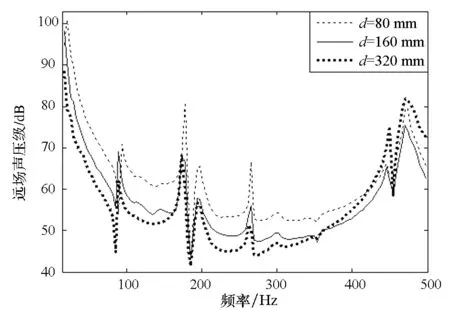
图10　气层厚度对气囊圆柱壳辐射声功率级与远场声压级的影响Fig.10　Influence of gas thickness to radiated power and far field sound pressure level of GCWCS

采用声无限元法分析气层厚度对气囊圆柱壳降噪效果的影响。将图7中的参数①～⑤与⑩分别扩大为2.2.1节中的二倍，远场点距点声源20 m。计算频带与步长不变。气体密度与声速分别设定为5.36 kg/m3与330 m/s，⑦分别为80 mm，160 mm，320 mm。计算各气囊圆柱壳湿表面辐射声功率级与远场声压级频响曲线，如图10所示。结果表明，在300 Hz以下，气体层厚增加，气囊圆柱壳的辐射声功率级与远场声压级均有明显下降。但在400～500 Hz频段，气体层厚为320 mm的圆柱壳的辐射声功率级与远场声压级的峰值高于气体层厚为80 mm与160 mm的圆柱壳，结论与1.2节相似。需要注意的是，图9与图10的曲线比图5与图6的曲线复杂。这是由于图5与图6是针对气体参数定性的机理分析所得的结果；而图9与图10反映的则是气囊圆柱壳整体的声学特性既受气体参数的影响，也受圆柱壳自身的模态等其他动力学特性[14]及内域水的影响。

2.3优化模型计算

基于以上结论，选择声速为258 m/s的CO2气体[15]充入气囊。为保证气囊外层蒙皮两侧压强一致，应对气囊内气体加压。将CO2气体等温加压至1 MPa，此时气体密度为19.8 kg/m3，声速仍为258 m/s。气囊圆柱壳尺寸与2.2.2节相同，气体层厚80 mm。分别计算裸圆柱壳与气囊圆柱壳的湿表面辐射声功率，并提取距各自点声源20 m处的远场点声压级。计算所得频响曲线如图11所示，130 Hz频点的湿表面位移云图与声压级云图如图12所示。结果表明：敷设CO2气囊的充水圆柱壳在30～500 Hz频段的辐射声功率与远场辐射声压均远小于充水裸圆柱壳。

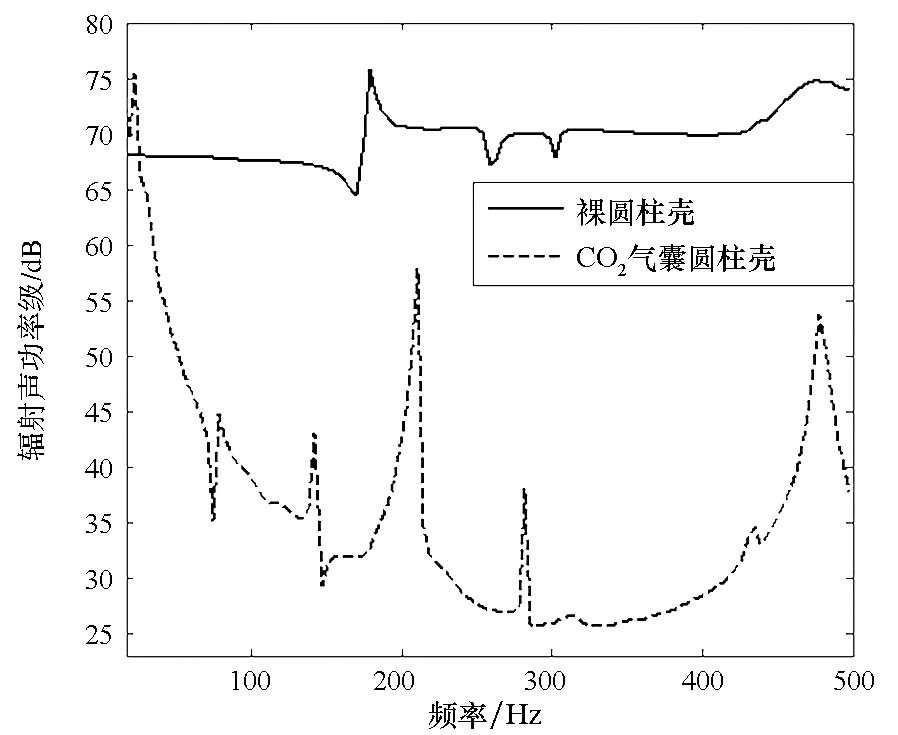
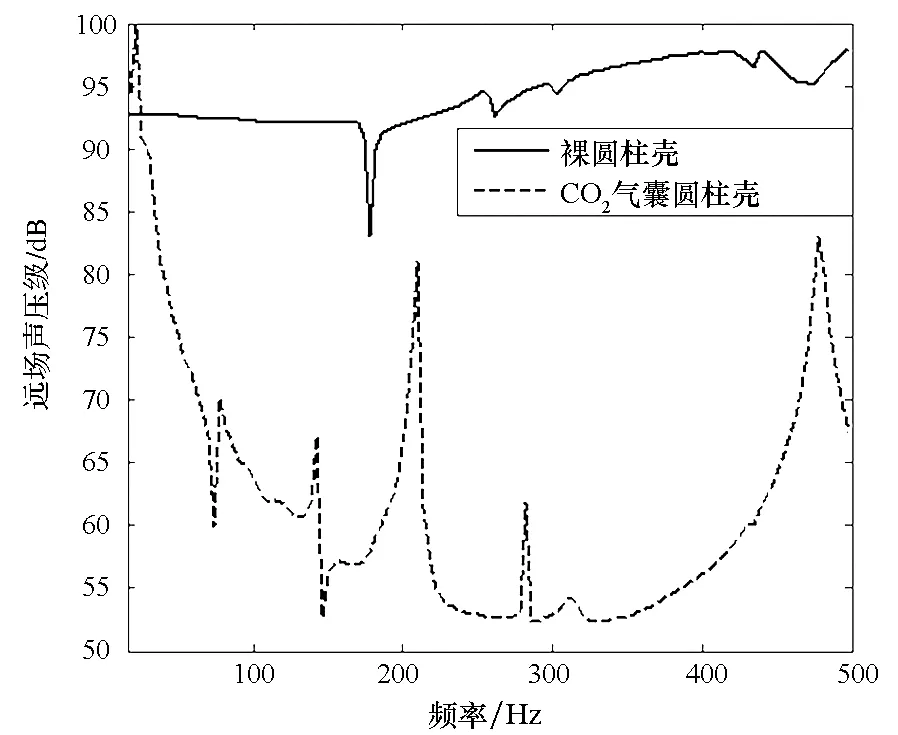
图11　充水CO2气囊圆柱壳的降噪效果Fig.11　Noise reduction effects of CO2-bag coated WCS

(a) 裸圆柱壳湿表面位移(a) Wet surface displacement contour of bare WCS

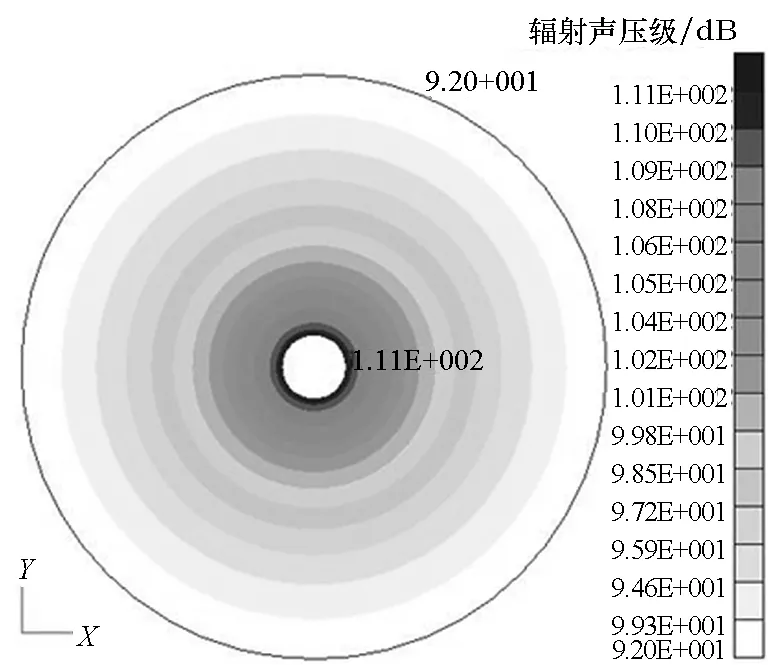
(b) 裸圆柱壳辐射声压级(b) Radiated sound pressure level of bare WCS

(c) CO2气囊圆柱壳湿表面位移(c) Wet surface displacement contour of CO2-bag coated WCS

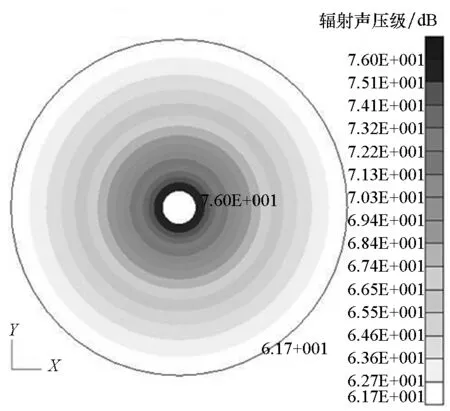
(d) CO2气囊圆柱壳辐射声压级(d) Radiated sound pressure level of CO2-bag coated WCS图12　裸圆柱壳与CO2气囊圆柱壳的湿表面位移与辐射声压云图Fig.12　Wet surface displacement contours and radiated sound pressure contours of bare and CO2-bag coated WCS

3结论

在充水裸圆柱壳上敷设气囊式声学覆盖层，形成了气囊圆柱壳。针对气体在整个系统中的作用，将充水裸圆柱壳和充水气囊圆柱壳分别简化为单、双层一维隔板。将入射声波设定为单频、斜入射的平面波，对单、双层隔板的声传播特性进行机理分析，采用MATLAB编程，分析了气体参数对双层隔板声辐射的影响。采用声无限元法，将机理分析中所得的规律应用于裸圆柱壳与气囊圆柱壳，计算了充水气囊圆柱壳和充水裸圆柱壳的水下湿表面辐射声功率与远场点声压级，优化设计出了CO2气囊圆柱壳。得出结论如下：

1) 平面波的入射角小于40°时(对文中的圆柱壳，点声源入射到外壳上任意位置的入射角均小于40°)，声速的变化对双层隔板降噪效果的影响规律比较一致。气体声速越小，双层隔板的降噪效果越好，频率越高，降噪效果越明显。该规律对充水气囊圆柱壳同样适用。

2) 谱峰的出现和气体层厚与气体中的声波长之比有关。可以通过选择适当声速的气体及其层厚，权衡频带上总的辐射噪声水平和谱峰的密集程度，进一步降低气囊圆柱壳的辐射声功率。

3) 有限长圆柱壳的水下辐射声功率在任一频率点的值是单频、入射角不同的声波叠加的结果。优化设计出的充水CO2气囊圆柱壳在点声源激励下的辐射声功率级与远场声压级明显低于充水裸圆柱壳。

参考文献(References)

[1]Cao X T, Hua H X. Sound radiation from shear deformable stiffened laminated plates with multiple compliant layers [J]. Journal of Vibration and Acoustics, 2012, 134(5): 051001.

[2]黄炎, 李种复, 杨光松. 复合材料弹性常数的直接测试[J]. 国防科技大学学报, 1984(01): 15-26.

HUANG Yan, LI Zhongfu, YANG Guangsong. Direct measuring for elastic constants of composite materials [J].Journal of National University of Defense Technology, 1984(01): 15-26. (in Chinese)

[3]Kerwin E M, Jr. Damping of flexural waves by a constrained viscoelastic layer [J]. Journal of the Acoustical Society of America, 1959, 31: 952-962.

[4]Berry A, Foin O, Szabo J P. Three-dimensional elasticity model for a decoupling coating on a rectangular plate immersed in a heavy fluid [J]. Journal of the Acoustical Society of America, 2001, 109(6): 2704-2714.

[5]Lu Y P, Killian J W,Everstine G C. Vibration of three layered damped sandwich plate composite [J]. Journal of Sound and Vibration, 1979, 64(1): 63-71.

[6]姚熊亮, 张阿漫, 钱德进， 等. 去耦瓦敷设方式对双层壳声振动的影响[J]. 海军工程大学学报, 2008, 20(2): 33-37.

YAO Xiongliang, ZHANG Aman, QIAN Dejin, et al. On effect of laying regions of uncoupled anechoic material on sound radiation of double cylindrical shell [J]. Journal of Naval University of Engineering, 2008, 20(2): 33-37.(in Chinese)

[7]白振国, 俞孟萨. 多层声学覆盖层复合的有限长弹性圆柱壳声辐射特性研究[J]. 船舶力学, 2007, 11(5): 788-797.BAI Zhenguo, YU Mengsa. Sound radiation of finite composite cylindrical shells with multi-layers acoustic coating[J]. Journal of Ship Mechanics, 2007, 11(5): 788-797. (in Chinese)

[8]Cao X T, Hua H X, Zhang Z G. Acoustic radiation from stiffened cylindrical shells with constrained layer damping[J]. Journal of Vibration and Acoustics, 2013, 135(1): 011005.

[9]Wang C, Lai J C S. The sound radiation efficiency of finite length acoustically thick circular cylindrical shells under mechanical excitation I: theoretical analysis [J]. Journal of Sound and Vibration, 2000, 232(2): 431-447.

[10]谭路, 纪刚, 张纬康, 等. 采用波数域方法分析细长柱壳的振动与声辐射特性[J]. 海军工程大学学报, 2013, 25(3): 66-71.

TAN Lu, JI Gang, ZHANG Weikang,et al. Slender cylindrical vibration and radiation by use of wave-number domain approach [J]. Journal of Naval University of Engineering, 2013, 25(3): 66-71. (in Chinese)

[11]Fahy F, Gardonio P. Sound and structural vibration [M]. 2nd ed. Oxford: Academic Press, 2007.

[12]Astley R J, Hamilton J A.The stability of infinite element schemes for transient wave problems [J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(29/30/31/32): 3553-3571.[13]Mertens T, Gamallo P, Astley R J. A mapped finite and infinite partition of unity method for convected acoustic radiation in axisymmetric domains[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197: 4273-4283.[14]汤渭霖, 何兵蓉. 水中有限长加肋圆柱壳体振动和声辐射近似解析解[J]. 声学学报, 2001, 26(1): 1-5.

TANG Weilin, HE Bingrong.Approximate analytic solution of vibration and sound radiation from stiffened finite cylindrical shells in water [J]. Acta Acustica, 2001, 26(1): 1-5. (in Chinese)

[15]杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京：南京大学出版社, 2012.

DU Gonghuan, ZHU Zhemin, GONG Xiufen. Fundamentals of acoustics [M]. Nanjing: Nanjing University Press, 2012.(in Chinese)

doi:10.11887/j.cn.201602030

*收稿日期：2015-08-22

基金项目：国家部委基金资助项目(9140A14080512JB115)

作者简介：段嘉希(1987—)，男，湖北仙桃人，博士研究生，E-mail：504179891@qq.com；周其斗(通信作者)，男，教授，博士，博士生导师，E-mail：qidou_zhou@126.com

中图分类号：U663.2

文献标志码：A

文章编号：1001-2486(2016)02-183-08

Acoustic radiation characteristics of gas-bag coated water-filled cylindrical shell

DUAN Jiaxi, ZHOU Qidou, ZHENG Han

(Department of Naval Ship Engineering, Naval University of Engineering, Wuhan 430033, China)

Abstract：In order to reduce the underwater radiated noise of WCS (water-filled cylindrical shell) excited by an interior point acoustic source, a gas-bag was coated on the outer surface to form the gas-bag coated cylindrical shell. In order to give instructions on the design of GCWCS (gas-bag coated water-filled cylindrical shell), the bare and the gas-bag coated WCS were respectively simplified into the single-leaf and the double-leaf partitions. By comparing the wave impedances of the partition, gas and water, the influences of the sound velocity and thickness of gas on the low frequency radiation of double-leaf partition with plane incidence sound wave were analyzed. Analysis results show that gases with smaller sound velocity and proper thickness have better radiation noise reduction effect. The acoustic infinite element method was employed to calculate the underwater acoustic radiation of GCWCS, whose results are in good accordance with those of the partition analysis. The underwater radiated sound power and the far-field radiation sound pressure of the optimized CO2-bag coated WCS are much lower than the bare one.

Key words：gas-bag coated cylindrical shell; partition; radiated acoustic power; sound velocity; infinite element method

http://journal.nudt.edu.cn