复杂系统脆弱性综合分析方法*

张旺勋，李　群，王维平，李海兵

(国防科技大学 信息系统与管理学院， 湖南 长沙　410073)



复杂系统脆弱性综合分析方法*

张旺勋，李群，王维平，李海兵

(国防科技大学 信息系统与管理学院， 湖南 长沙410073)

摘要：为全面识别复杂系统中的脆弱点，科学评价其脆弱性，针对纯拓扑脆弱性分析方法的不足，在考虑非拓扑因素条件下，提出一种结合复杂网络技术和效能评估技术的复杂系统脆弱性综合分析方法，从拓扑结构和非拓扑因素两方面全面分析复杂系统的脆弱性。以复杂网络的中心性指标为基础，通过广义指标法进行拓扑脆弱性分析；借鉴概率风险评价理论，从易攻性和易坏性两个方面对非拓扑脆弱性进行评价；通过对两者结果的综合得到总的脆弱性分析结果。示例结果表明：拓扑和非拓扑分析的结果有交集但又有所区别，两者密切相关且互为补充，并能共同筛选出复杂系统中的关键环节。较之纯粹的拓扑结构分析，综合分析得到的结果更为全面。

关键词：复杂系统；脆弱性；复杂网络；效能评估；拓扑

脆弱性表示系统容易受到攻击或容易被破坏的趋势，描述系统的不完美性、缺陷性或容易受到破坏的性能；而脆弱点是系统中比较薄弱的、有缺陷的节点或链路，一旦失效将造成严重后果[1-2]。

复杂系统一般由众多子系统和关系链路组成，其中一些关键核心节点或链路即脆弱点一旦失效、发生故障或被攻击，整个系统可能瘫痪。从攻防对抗的角度，军事复杂系统中的脆弱点具有至关重要的军事和战略价值，一般是敌方首选的攻击对象，也是己方防护的要点。同时脆弱性研究对能源、航天、生态等民用领域同样具有重要价值[1, 3-4]。

当前关于复杂系统重要节点、重要链路的挖掘大多是针对拓扑结构的[5-6]，但节点或链路的重要性显然不仅与它在网络中的拓扑位置有关，还与其功能、角色、物理位置等属性有关。虽然系统的拓扑结构决定了其功能，但研究表明纯拓扑结构的分析方法忽视了系统的物理属性、运行特征等信息，不能把握其他有关系统安全性的重要方面[7]，单独依靠拓扑结构模型并不能为系统的脆弱性分析提供充足的信息[8]，甚至可能会产生错误的结论[9]。因此，不能仅依赖拓扑结构分析进行评价或决策，而需要将其与其他建模方法结合，兼顾功能、逻辑关系等非拓扑层面的因素[10]，从而提供更全面综合的评价结果和决策支持[11]。

为此，张旺勋等从复杂系统的拓扑结构和非拓扑因素两方面，分析不同节点和链路的重要度，识别网络中的关键节点和链路，筛选出网络的脆弱点，并根据脆弱点的数量、威胁程度等给出总体的脆弱性评价。

1分析框架

为更全面科学地研究复杂系统的脆弱性，结合前文的现状分析和定义描述，考虑非拓扑因素的脆弱性分析。目的是从脆弱性相关的拓扑结构和非拓扑因素出发，结合复杂网络理论和其他效能评估分析技术，找出体系中最重要的节点和边，并对体系脆弱性进行度量和评价，基于此提出了基于复杂网络-综合效能评估(Complex Networks & Comprehensive Effectiveness Assessment，CNEA)的复杂系统系脆弱性综合分析方法，分析框架如图1所示。

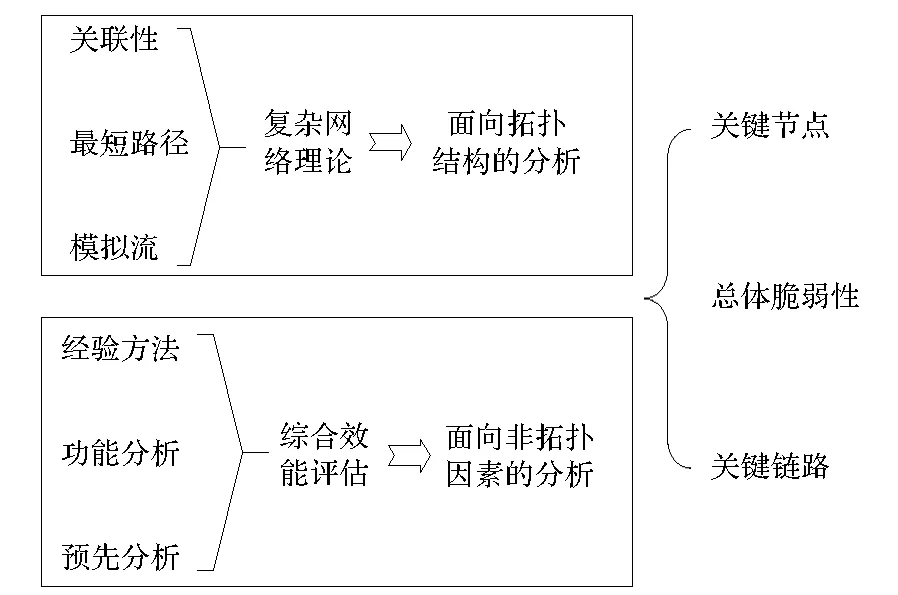
图1　复杂系统脆弱性综合分析框架Fig.1　Framework for comprehensive vulnerability analysis of complex systems

复杂系统脆弱性分析包括面向拓扑结构的分析和面向非拓扑结构的分析。其中拓扑结构表示与体系中组分系统的功能、角色、形状、大小等细节无关，仅与系统之间有无联系相关的，用点和线描述的体系结构图。面向拓扑结构的脆弱性分析，主要根据复杂网络理论即方法的CN部分，通过相关的拓扑统计特征和方法来筛选系统中的关键节点和关系[5, 12]。非拓扑结构的脆弱性，则根据体系脆弱性的定义，考虑除拓扑结构以外的与“易受攻击、易被破坏”相关的因素，如功能角色对使命任务或关键能力的重要性、被攻击或失效的难易程度和概率、失效后对系统的影响程度等。面向非拓扑结构的脆弱性分析，主要以多指标的综合效能评估方法为主[4]，即方法的EA部分。

需要说明的是，面向拓扑结构的脆弱性分析和面向非拓扑结构的脆弱性分析分别代表了脆弱性的不同方面，考虑的是不同因素：非拓扑分析较全面，但具有一定的主观性，拓扑分析更为客观，但不够全面。但两者并不矛盾，而是相互补充的，方向一致的。只有综合考虑，才能得到全面合理的结论。

2分析方法

2.1基于复杂网络的拓扑脆弱性分析

复杂网络为网络脆弱性研究引入了新的概念和方法，建立了拓扑结构和网络脆弱性的联系[13]。通过复杂网络的相关理论，研究面向拓扑结构的体系脆弱性分析方法。

常见的评价重要节点和边的拓扑指标有很多种，其中中心性指标是直接反映网络各节点和链路相对重要性的因素，包括度中心性、介数中心性、特征向量中心性等[14]。

脆弱节点挖掘方面，以节点度中心性CD(vi)、介数中心性CB(vi)、特征向量中心性CX(vi)3个指标为基础，通过广义指标法将3个指标通过加权聚合得到一个总的重要度值，具体方法如下：

1)用S1,S2,S3分别表示由所有节点的节点度中心性、介数中心性和特征向量中心性按照数值从大到小排序组成的数值序列，分别用Mx1=max{CD(vi)}，Mx2=max{CB(vi)}，Mx3=max{CX(vi)}表示其中的最大值。

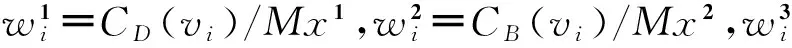
3)对所有节点，其总得分w(vi)的计算公式为：

(1)

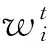
4)为便于与之后的边重要度综合处理，对所有节点的总得分归一化，得到最终的节点重要度W(vi)，其计算公式为：

W(vi)=w(vi)/max{w(vi)}

(2)

脆弱边方面，以边介数中心性为评判标准，其重要度计算方法如下：

1)用S4表示由边的介数中心性按照数值从大到小的排序组成的数值序列，并记最大值为Mx4=max{CB(ei,j)}。

2)根据最大值，对所有边的介数中心性归一化，边的重要度记为：

(3)

根据重要度指标，则可以计算系统的脆弱性。但前提是该系统要是拓扑结构脆弱的，下面给出复杂系统拓扑脆弱的定义。

定义1(复杂系统拓扑脆弱)用M和N分别表示复杂系统拓扑结构中边和节点的总数；S1,S2,S3分别表示所有节点的节点度中心性、介数中心性和特征向量中心性按照数值从大到小的排序，S4表示所有边的介数中心性照数值从大到小的排序，用St(t=1,2,3,4)表示上述4个序列，Gt表示St序列中取值的个数，且Gt≤N。那么，复杂系统是拓扑脆弱的，必须满足条件1或者同时满足条件2与条件3。

1)M≤N-1；

2)∃t0∈{1,2,3,4}，使得Gt0>1；

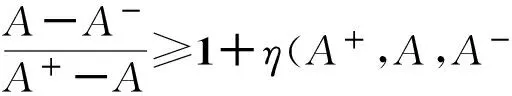
条件1拓扑结构中的边数量较少，仅有1个节点或1条边异常，将导致孤立点出现或体系不连通。这种网络是拓扑脆弱的。

条件2表明从拓扑结构角度，体系中的节点或边是有差异的。

条件3在条件2的基础上，若某个拓扑统计值体现了网络的差异性，且有两种取值，则至少较大值A要比较小值B大η倍(η与具体系统的具体任务场景相关)，此时取值为A的点或边为脆弱点，网络是拓扑脆弱的。若有两个以上取值，则多个取值最少存在一个很明显的拐点A，此时取值大于A的点或边为脆弱点，网络是拓扑脆弱的。若所有拓扑统计差异不大，即没有特别与众不同的关键点或边，则网络也不是拓扑脆弱的。同样这个“拐点”与具体武器装备体系的具体任务场景相关。

定义复杂系统拓扑脆弱性VT为：

(4)

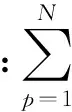
2.2基于效能评估的非拓扑脆弱性分析

从节点的功能、分类、运行等非拓扑方面考察复杂系统中子节点和通信链路的重要性，筛选系统的关键环节并评价其脆弱性。

复杂系统非拓扑信息的多样性、复杂性使得面向非拓扑因素的脆弱性分析面临众多困难，如系统类型多样、指标参数差异较大、历史数据不足、定量化数据较少等，从而非拓扑脆弱性分析应该以专家经验法、层次分析法、模糊评估方法等[15]定性半定性或模糊方法为主。

根据脆弱性定义，节点或链路即薄弱环节的筛选需要从易受攻击或失效、易被破坏两方面考虑。从而将脆弱性角度出发的节点或链路关键程度评价的顶层指标记为Li，其主要受易攻性Pa和严重性Se两方面指标的影响。

易攻性Pa指节点或链路被破坏或摧毁的发生概率和难易程度，该指标与其在复杂系统中的地位、攻击实施成本、攻击技术水平以及现有的防护水平等因素有关。

易坏性Se指节点或链路被破坏摧毁后对整个复杂系统造成的影响，与该节点或链路被破坏后造成的性能降阶、影响时间、影响范围等相关。

系统或链路越容易被摧毁且摧毁后的影响越严重，则这个地方就是复杂系统的重要薄弱环节。若将易毁性分为极易、容易、困难、特难四个等级，严重性分为灾难、严重、轻度、轻微四个等级。链路或节点的重要度可以根据这两者的级别组合得到，一种较简单直观的算法是根据两者的乘积得到。

Li=Pa×Se

(5)

当然，还可以通过更详细的指标分解，由下层具体的指标聚合得到易攻性和严重性指标，此处不再赘述。表1给出了根据乘积方法计算得到的不同易毁性和严重性组合得到的重要度数值，数值越高表示该节点或链路在系统中越薄弱、越关键，是防护的重点。

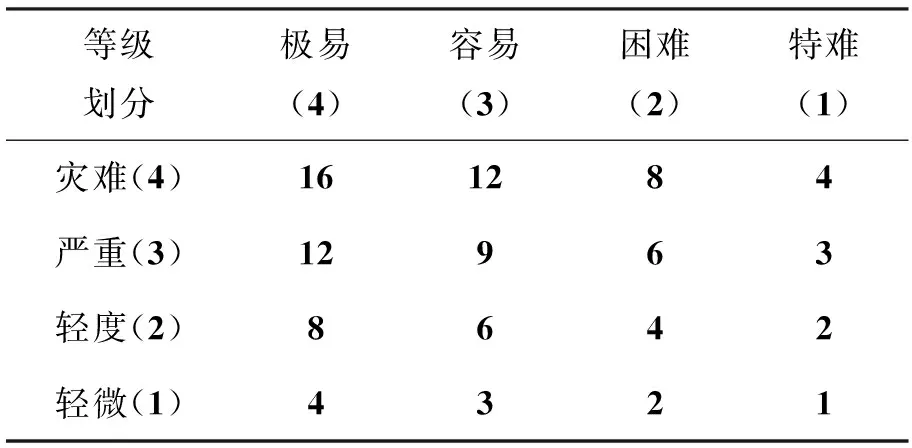
表1　非拓扑重要度评价表

根据上述指标获取到节点或链路的重要度之后，根据定义2和定义3识别哪些是脆弱点，并判断复杂系统是否为非拓扑脆弱的。

定义2(复杂系统非拓扑脆弱)复杂系统称为非拓扑脆弱的，须满足以下三个条件之一。

1)∃ob∈V∪E，Pa(ob)=极易；

2)∃ob∈V∪E，Se(ob)=灾难；

3)∃ob∈V∪E，Li(ob)≥8。

其中：V和E分别表示复杂系统中的节点集合和链路(关系)集合；ob表示任意的节点或链路(关系)。这三个条件是“或”的关系，即只需满足任意一个，则可以判定该节点或链路是非拓扑脆弱的。

同时根据定义2，给出节点或链路是否为脆弱点的判断定义3。

定义3(非拓扑脆弱点)复杂系统中的节点或链路ob称为非拓扑脆弱点，须满足以下三个条件之一。

1)Pa(ob)=极易；

2)Se(ob)=灾难；

3)Li(ob)≥8。

定义复杂系统的非拓扑脆弱性为：

(6)

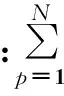
2.3脆弱性综合分析

2.1～2.2节分别从拓扑结构和非拓扑结构两方面分析了系统脆弱性。本节对这两部分的结果进行综合，给出系统总的脆弱性评价。

2.3.1脆弱点筛选

记根据拓扑结构筛选出来的节点集合和链路集合分别为TNS和TES；非拓扑评价得出的重要节点与链路的集合分别为CNS和CES，则综合网络拓扑结构和非拓扑结构的功能、属性等筛选出来的重要节点和重要链路集合分别记为VNS和VES，且有：

VNS=TNS∪CNS

(7)

VES=TES∪CES

(8)

2.3.2脆弱性评价

根据拓扑结构和非拓扑综合评价得到的脆弱性分别代表了脆弱性的两个不同方面，前者(ST)是纯粹从拓扑抗毁性出发的；后者(SC)则考虑角色功能、分类等非拓扑信息。对于这两个指标的处理，可以根据指标综合方法将两者融合得到一个指标，即NS=k1ST+k2SC；或者根据木桶原理取最薄弱的(最大值)得到一个总的评价值，即NS=max(ST,SC)；亦或是由两者组成的综合安全性向量表示，即NS=[ST,SC]。具体分析过程中，分析者可以根据需要选择不同的方法。

3示例分析

以美军的弹道导弹防御系统(Ballistic Missile Defense System，BMDS)为例，对提出的CNEA方法进行演示验证。

BMDS并无固定结构，它通过若干指控节点将一系列传感器和拦截武器集成为一个整体。理论上，BMDS允许范围内任何传感器与任何拦截武器关联[16]。根据BMDS的现状和网络化防空的发展趋势[17-18]，分析中心化和网络化两种不同结构下BMDS(分别记为A-BMDS和B-BMDS)的脆弱性。

用无向网络表示两种不同的结构，分别如图2和图3所示，节点代表S1～S11不同的系统，包括指控节点以及不同防御阶段的传感器节点和火力节点；边表示系统之间的情报、指控、协同等关系。

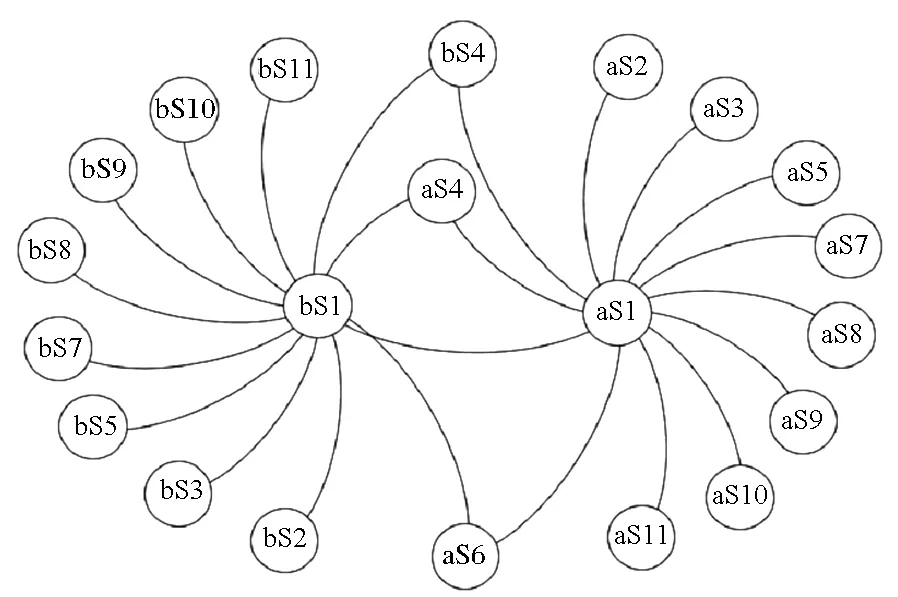
图2　A交互关系图Fig.2　Interaction relationships of A

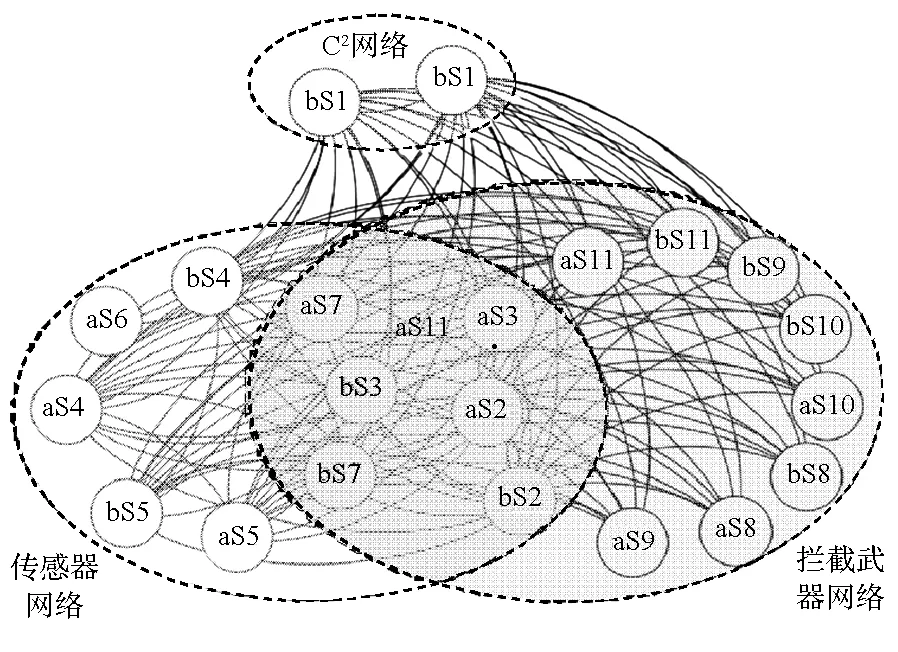
图3　B交互关系图Fig.3　Interaction relationships of B

根据前文给出的脆弱性分析方法及计算公式，中心化BMDS和网络化BMDS脆弱点、拓扑脆弱性(VT)、非拓扑脆弱性(VNT)等的分析和比较结果如表2和图4所示。

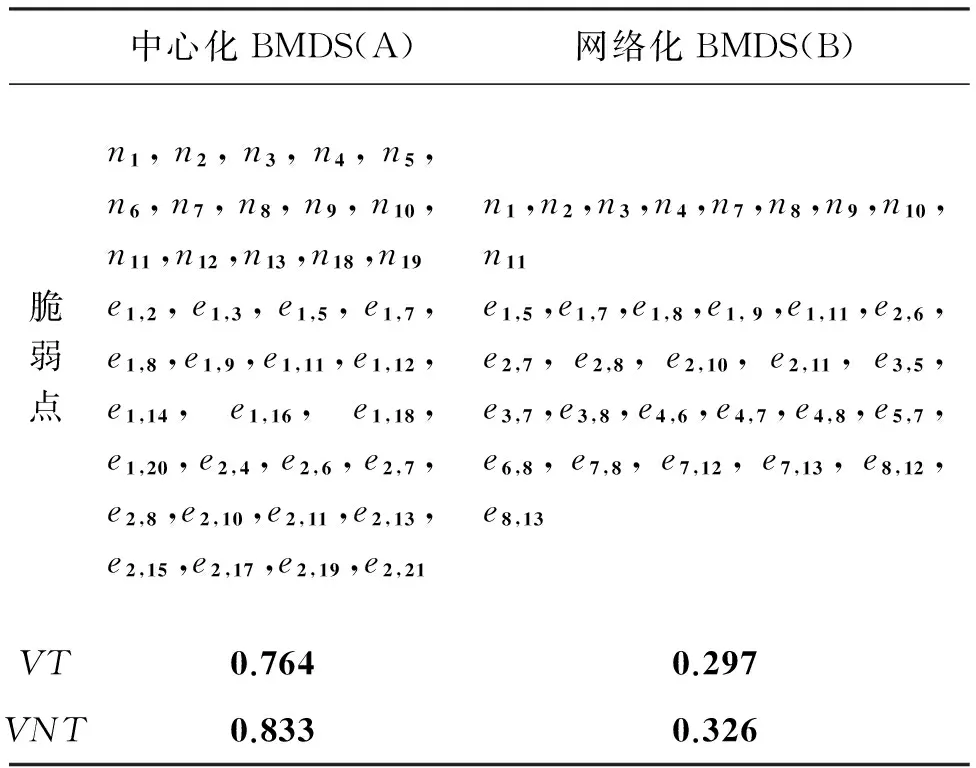
表2　脆弱性分析结果

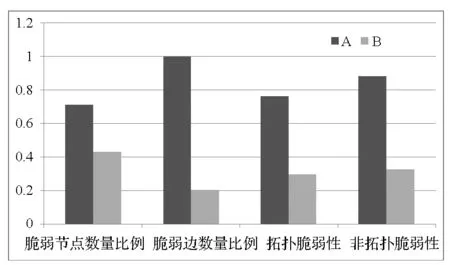
图4　两种结构脆弱性数据比较Fig.4　Vulnerability compare between A and B

根据上述数据可知：

1)从脆弱性角度考察，B明显优于A：B中脆弱节点和脆弱边的数量比例明显少于A；B的拓扑脆弱性和非拓扑脆弱性都明显小于A。

2)由于侧重点不同，拓扑和非拓扑分析的结果是有所区别的；同时由于结构和功能的关联关系，两个角度筛选出的结果是有交集的，并且结果较为接近的。

3)拓扑分析和非拓扑分析密切相关且互为补充，共同筛选出复杂系统中的关键环节，较之纯粹的拓扑结构分析，综合分析得到的结果更为全面。

4结论

针对纯拓扑脆弱性分析的不足，提出一种结合复杂网络技术和综合效能评估技术的复杂系统脆弱性综合分析方法。

1)明确了复杂系统脆弱性综合分析的基本概念，提出了脆弱性分析的思路框架。

2)提出了基于复杂网络理论的复杂系统拓扑脆弱性分析方法。从拓扑结构角度筛选复杂系统中的关键节点和链路，并通过指标对拓扑脆弱性进行评价。

3)借鉴系统安全性评价中有关风险发生概率和风险后果的处理方法，提出了基于综合效能评估的非拓扑脆弱性分析方法，通过易攻性和易坏性两个指标及其乘积来评价节点或链路的重要程度。

4)根据拓扑脆弱性和非拓扑脆弱性的辩证关系，综合筛选出复杂系统的关键节点和链路，并得到了总的脆弱性结果。

5)以BMDS系统为例，对比了两种不同结构BMDS的脆弱性，结果符合军事理论常识和现实，验证了CNEA方法的科学性。

参考文献(References)

[1]王博. 复杂电力系统安全风险及脆弱性评估方法研究[D]. 武汉: 华中科技大学, 2011.

WANG Bo. Research on security risk and vulnerability assessment method for complicated power system[D]. Wuhan: Huazhong University of Science and Technology,2011.(in Chinese)

[2]张怡, 赵凯, 来犇. 警报关联图：一种网络脆弱性量化评估的新方法[J]. 国防科技大学学报, 2012, 34(3): 109-112.

ZHANG Yi, ZHAO Kai, Lai Ben. Alert correlation graph: a novel method for quantitative vulnerability assessment[J]. Journal of Nation University of Defense Technology, 2012, 34(3): 109-112. (in Chinese)

[3]Zhang W X, Hou H T, Li Q, et al. Vulnerability analysis of the global navigation satellite systems from the information flow perspective[C]//Proceedings of 6th International Conference on Information Management, Innovation Management and Industrial Engineering, Xi′an, IEEE, 2013： 263-267.

[4]邹君. 湖南生态水资源系统脆弱性评价及其可持续开发利用研究[D]. 长沙: 湖南师范大学, 2010.ZOU Jun. Vulnerability evaluation and its sustainable utilization of eco-water resource system in Hunan province[D]. Changsha: Hunan Normal University, 2010. (in Chinese)

[5]吴俊. 复杂网络拓扑结构抗毁性研究[D]. 长沙: 国防科学技术大学, 2008.

WU Jun. Study on invulnerability of complex network topologies[D]. Changsha: National University of Defense Technology, 2008. (in Chinese)

[6]郭世泽, 陆哲明. 复杂网络基础理论[M]. 北京: 科学出版社, 2012: 63.

GUO Shize, LU Zheming. The basics of complex networks[M]. Beijing: Science Press, 2012: 63. (in Chinese)

[7]Bompard E, Napoli R, Xue F. Extended topological approach for the assessment of structural vulnerability in transmission networks[J]. IET Generation, Transmission & Distribution, 2010, 4 (6): 716-724.

[8]Hines P, Cotilla-Sanchez E, Blumsack S. Do topological models provide good information about vulnerability in electric power networks?[J]. Chaos, 2010, 20 (3): 033122.

[9]Hines P, Cotilla-Sanchez E, Blumsack S. Topological models and critical slowing down: two approaches to power system blackout risk analysis[C] //Proceedings of 44th Hawaii International Conference on System Sciences, Hawaii, IEEE, 2011: 1-10.

[10]金伟新. 体系对抗复杂网络建模与仿真[M]. 北京: 电子工业出版社, 2010.JIN Weixin. SoS-Ops M&S based on the complex network[M]. Beijing: Electronic Industry Press, 2010. (in Chinese)

[11]Ouyang M. Review on modeling and simulation of interdependent critical infrastructure systems[J]. Reliability Engineering & System Safety, 2014, 121(1): 43-60.

[12]王智源, 丁泽中, 胡广水. 军事通信网络拓扑结构抗毁性仿真[J]. 计算机系统应用, 2010, 19 (12): 109-113.

WANG Zhiyuan, DING Zezhong, HU Guangshui. Invulnerability simulation of military communication networks topology[J]. Journal of Computer Applications, 2010, 19(12): 109-113. (in Chinese)

[13]Guo C, Zhao Z D, Hill D J,et al. Attack structural vulnerability of power grids: a hybrid approach based on complex networks[J]. Physica A: Statistical Mechanics and its Applications, 2010, 389(3): 595-603.

[14]何大韧, 刘宗华, 汪秉宏. 复杂系统与复杂网络[M]. 北京: 高等教育出版社, 2009.

HE Daren, LIU Zonghua, WANG Binghong. Complex system and complex network[M]. Beijing: Higher Education Press,2009. (in Chinese)

[15]石福丽, 方志刚, 杨峰, 等. 基于仿真的潜艇装备作战能力ANP幂指数评估方法[J]. 国防科技大学学报, 2011, 33 (4): 168-174.

SHI Fuli, FANG Zhigang, YANG Feng, et al. ANP power index evaluation method for operational capability of submarine equipment based on simulation[J]. Journal of National University of Defense Technology, 2011, 33 (4): 168-174. (in Chinese)

[16]Redmond P J. A system of systems interface hazard analysis technique[D]. USA: Naval Postgraduate School, 2007.

[17]唐苏妍. 网络化防空导弹体系动态拦截联盟形成机制与方法研究[D]. 长沙: 国防科学技术大学, 2011.

TANG Suyan. Research on dynamic interception coalition formation mechanism and method in networked air defense missile systems[D]. Changsha: National University of Defense Technology, 2011. (in Chinese)

[18]朱智, 雷永林, 朱宁, 等. 面向网络化防空反导体系的可组合建模框架[J]. 国防科技大学学报, 2014, 36 (5): 186-190.

ZHU Zhi, LEI Yonglin, ZHU Ning,et al. Composable modeling frameworks oriented networked air & missile defense systems[J]. Journal of National University of Defense Technology, 2014, 36 (5): 186-190. (in Chinese)

doi:10.11887/j.cn.201602025

*收稿日期：2015-03-26

基金项目：国家自然科学基金资助项目(91024015)

作者简介：张旺勋(1985—)，男，陕西韩城人，博士研究生，E-mail：zhangwangxun2010@163.com；王维平(通信作者)，男，教授，博士，博士生导师，E-mail：wang.wp2010@gmail.com

中图分类号：TN967.1

文献标志码：A

文章编号：1001-2486(2016)02-150-06

Comprehensive analysis method for vulnerability of complex systems

ZHANG Wangxun, LI Qun, WANG Weiping, Li Haibing

(College of Information System and Management, National University of Defense Technology, Changsha 410073, China)

Abstract：In order to identify vulnerable points in complex system roundly and assess its vulnerability scientifically, to improve the insufficiency of the pure topological methods, an analysis method integrated complex network theories and effectiveness assessment technologies was proposed, which considers both the topological and non-topological factors of vulnerability. Based on centricity measurements of complex network, a generalized indicators method was used for topological vulnerability analysis. Referring to the probability risk assessment theory, non-topological vulnerability was analyzed from susceptibility and brittleness. Then the final vulnerability results were integrated from the former two results. The demonstration results show that there is an intersection set but also some differences between topological and non-topological analysis. These two aspects of vulnerability are correlative and complementary close, they both contribute to the screening of critical points and links in a complex system, and compared to purely topological study, conclusions from integrated analysis were more comprehensive.

Key words：complex system; vulnerability; complex network; effectiveness assessment; topology

http://journal.nudt.edu.cn