非理想信道下测量零值无偏干扰抑制滤波器设计*

范广腾，倪少杰，唐小妹，陈华明，孙广富

(国防科技大学 电子科学与工程学院， 湖南 长沙　410073)



非理想信道下测量零值无偏干扰抑制滤波器设计*

范广腾，倪少杰，唐小妹，陈华明，孙广富

(国防科技大学 电子科学与工程学院， 湖南 长沙410073)

摘要：现有的抗干扰滤波器在通道非理想特性下会导致接收机测量零值发生偏移，且偏移量与干扰参数相关，其已成为高精度测距接收机实现其精度提升的主要障碍。针对上述问题，从对称通道特性出发，给出一种无偏的时域抗干扰滤波器设计技术。解决了传统的时域抗干扰滤波器在非理想信道下测量零值偏移的问题，且工程实现简单。理论分析和仿真实验进一步验证了方法的有效性，采用该方法可以使测量零值偏移小于0.2 ns。

关键词：非理想信道；干扰抑制滤波器；零值偏移；高精度测量

地面接收到的全球导航卫星系统(Global Navigation Satellite System, GNSS)信号强度在-130 dBm左右，远在噪声之下[1]。随着定位功能越来越多地集成到移动设备中，由其他通信设备泄漏到GNSS信号频段的干扰不断增多。这些干扰严重降低卫星导航接收机的性能。其中对GNSS接收机影响最大，且最常见的干扰类型是窄带干扰[2]。因此，目前的GNSS接收机普遍都会装有抗窄带干扰设备。其中基于线性估计的时域干扰抑制技术基础理论成熟，实现时硬件规模小，可在单片现场可编程门阵列中实现，便于模块化；可有效抑制连续波干扰、脉冲连续波及扫频连续波等窄带干扰；还可与空域干扰抑制技术有效结合[3]。鉴于这些优点，在导航接收机中广泛采用该技术。

在卫星导航系统中，既要有效地抑制干扰，同时还要尽可能地降低干扰抑制技术对系统测距性能的影响。现有的自适应干扰抑制滤波器在假定输入相关峰为理想对称的前提下，通过对滤波器系数进行约束，可以达到不改变测量零值的目的[4]。但是实际的接收机，由于接收通道的非理想特性会对输入信号的相关峰产生畸变，从而输入至自适应干扰抑制滤波器的信号其相关峰不再满足对称性要求。因此上述的抗干扰措施会导致接收机测量零值发生偏移，且偏移量与抗干扰参数相关。当输入的干扰信号特性发生变化时，测量零值也会随之发生波动，因此传统的对接收机测量零值事先标校的方法将会失效[5-6]。

由抗干扰带来的测距值偏移已成为实现高精度测距接收机提升其精度的主要障碍。现有的文献中也介绍了消除测量零值偏移的方法，主要分为两大类。一类是通过在模拟通道后面增加校准滤波器消除接收通道的非理想因素，该技术又分为模拟域的均衡技术和数字域的校准技术[7-9]。模拟域的均衡技术一般采用电感电容等模拟元件搭建均衡网络，这种均衡网络具有均衡精度较差、均衡适用性不广的缺点。数字域的校准技术通常运算复杂度高，且精度不好控制。另一类方法采用小环路自校的方式对接收机的测量零值进行校正。但是发射信道特性和接收信道特性的耦合作用可能导致时延校正值出现偏差[10]，并且该方法会增加一个专门用于校准的发射通道和一个专用于校准的接收通道，大大增加了硬件的复杂度。

针对上述问题，范广腾等提出了一种非理想信道下测量零值无偏的干扰抑制滤波器技术，该技术利用了接收通道幅频响应和群时延响应对称的特点，通过增加了一个与传统的干扰抑制滤波器幅频响应互补的补偿滤波器，达到消除测量零值偏移的目的。该技术实现简单，可以用于需要同时满足抗干扰和测距指标要求的低成本接收机中。

1非理想信道下干扰抑制滤波器对测量零值的影响

1.1非理想信道对输入信号相关峰的影响

包含干扰抑制滤波器的时延估计框图如图1所示，其中s(t)为天线口面接收到的伪码信号；w(t)为等效到天线口面的热噪声，为高斯白噪声；j(t)为干扰信号；hLP(t)为理想低通滤波器；h(t)为接收通道滤波器等综合引起的滤波效果；ha-jam(n)为干扰抑制滤波器；早迟码估计器分为相干和非相干两种形式。图1中的时延估计模型采用的都是信号的基带形式。

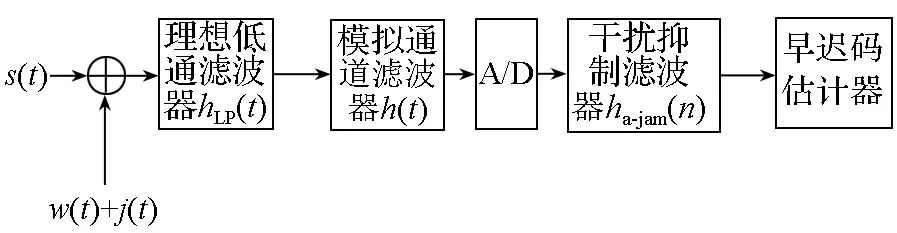
图1　包含自适应抗干扰滤波器的时延估计框图Fig.1　Block diagram of time delay estimator include adaptive anti-jamming filter

图1中基带信号s(t)的表达式为：

s(t)=AD(t)c(t)ej(2πfdt+θ)

(1)

其中：A为基带信号幅度；D(t)为调制的数据信息，当时延估计在1 bit信息内进行时，可以忽略此调制信息；c(t)为扩频码时域波形，码宽为Tc；fd为接收信号的多普勒频偏；θ为载波相位初值。

高斯白噪声w(t)的复数形式为：

w(t)=wi(t)+j·wq(t)

(2)

其中，wi(t)和wq(t)是互相独立双边功率谱密度等于N0的高斯白噪声。

为了方便分析，将实际的通道滤波器分为理想低通滤波器和通道滤波器两个部分。

在实际应用中，每个系统都给定了一定的频谱带宽，带宽外存在其他应用系统的信号，若不加滤除，经过数字采样后将会混叠至带内，影响时延估计的性能，在恶劣情况下甚至使其失效。理想低通滤波器hLP(t)就起到限带的作用，其傅里叶变换为：

(3)

h(t)模拟了接收通道中各级滤波器的综合效果，其傅里叶变换为：

H(f)=A(f)exp[jφ(f)]

(4)

其中，Α(f)和φ(f)分别为滤波器的幅频响应和相频响应。

滤波器的群时延定义为：

(5)

一般情况下，群时延是频率的函数。若满足τg(f)为常数，τ0与f无关，则称该滤波器为线性相位滤波器，此时φ(f)=-2πfτ0。

线性相位滤波器的一个性质是，若A(f)≡1，则输入信号s(t)经过线性相位滤波器之后为s(t-τ0)。即除了在时间上有延迟，其波形与输入的完全相同。

实际应用中，并不能保证这种理想的恒幅度线性相位滤波器，从而滤波器响应的幅度和相位是f的函数。这种情况下，经过滤波器之后的信号会引起失真，从而影响时延的估计。

根据文献[10]可知，经过非理想信道后的相关峰为：

(6)

不同阶段的相关峰如图2所示。由图2可知，经过理想低通滤波器后的相关峰虽然顶部变得平坦但相关峰依然保持对称。但是经过非理想信道滤波器后，相关峰发生了畸变，不再保持对称。

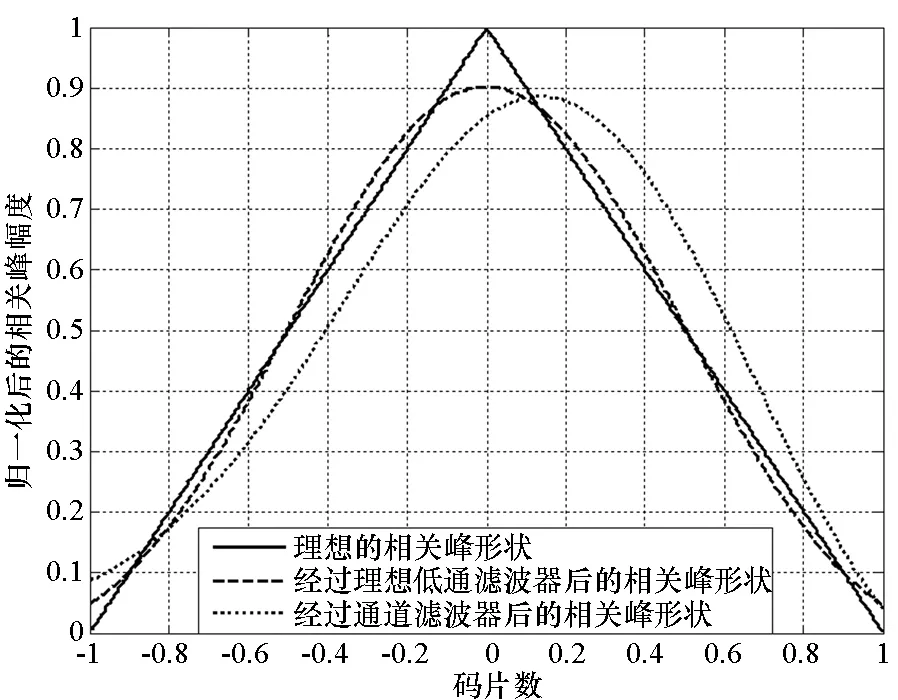
图2　不同阶段的相关峰Fig.2　Correlation function in different stages

1.2干扰抑制滤波器对测量零值的影响

由文献[4]可知，干扰抑制滤波器的系数为共轭对称，其频率响应为实函数，令其为Ha-jam(f)。则经过干扰抑制滤波器后的相关函数为：

(7)

若采用相干早迟码时延估计器，则其鉴相函数为：

γ(ε)=Re[ya-jam(τ+d/2)]-Re[ya-jam(τ-d/2)]

(8)

早迟码估计器所估计的测量零值ε使得γ(ε)=0。即有：

(9)

当ε·b≪1，关于ε泰勒展开并取一阶近似，可得：

(10)

由式(10)可知，测量零值与自适应干扰抑制滤波器的幅频响应有关，而自适应干扰抑制滤波器的幅频响应又与外部输入的干扰信号特性有关，当干扰特性发生变化时，抗干扰滤波器的幅频响应也会随之变化，从而会导致测量零值发生波动。且相对于幅频特性，群时延非理想特性对相关峰畸变的影响更大，其与测量零值的关系更加密切[11]，如图3所示。

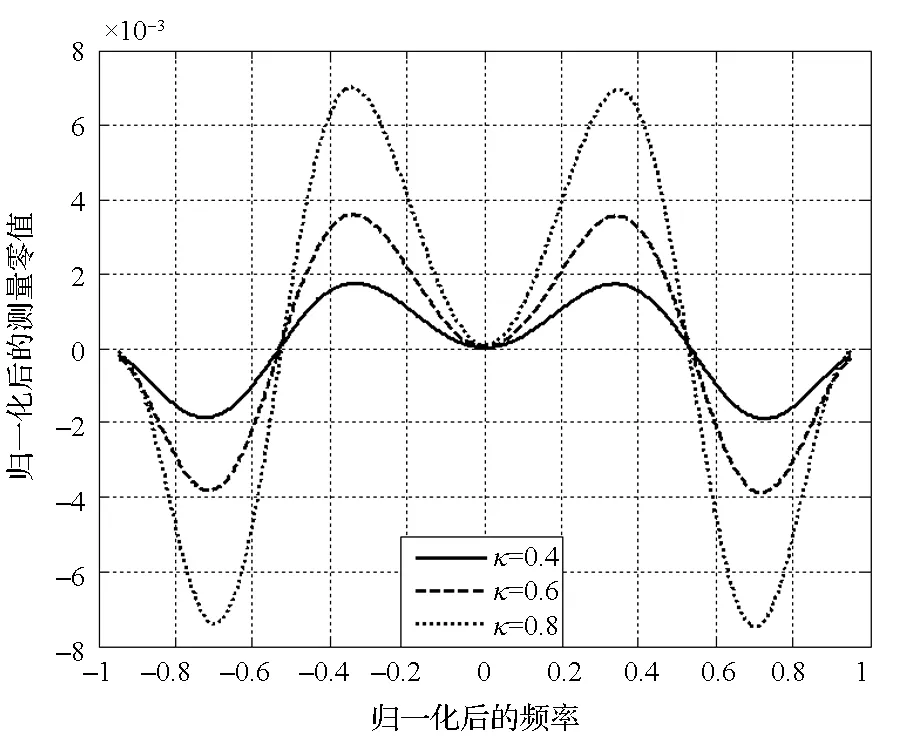
图3　不同κ值时干扰频率对应测距零值的波动Fig.3　Bias-value vs jamming frequency in different κ

图3中采用的相关间隔为0.2个码片，通道滤波器模型幅频响应为常数，群时延响应是二次函数，其模型为：

(11)

其中，κ是对变化剧烈程度的描述，τg(f)的单位是Tc，归一化后的干扰带宽为0.1。由图3可知，测量零值的波动幅度与畸变系数有关，畸变系数越大，波动幅度也越大。

2幅频补偿的时域抗干扰滤波器设计

在介绍该方法之前，首先对模拟通道滤波器的特性进行分析。虽然实际工程使用的模拟通道很难满足理想通道的条件，但是在设计中一般会保证通道的冲击响应h(t)为实函数。若通道的冲击响应h(t)为复函数，则输入伪码信号将有一部分能量泄漏到正交通道，而且无法通过相位旋转的方法消除。这是工程设计中不被期望的，因为能量泄漏意味着性能的损失，如误码率提高、跟踪精度下降等。当h(t)为实函数时，若其傅里叶变换为H(f)=A(f)exp[jφ(f)]，则幅频响应A(f)为偶函数，相频响应φ(f)为奇函数，对φ(f)求导可得通道的群时延响应τg(f)为偶函数。因此在实际非理想通道中，幅频响应和群时延响应对称的通道特性是工程中最常见，也是除理想通道特性外工程中最希望达到的一种通道特性。范广腾等正是基于通道的对称特性提出了对测量零值的幅频补偿方法。

在干扰抑制滤波器后增加与其幅频响应互补的补偿滤波器来消除由于干扰抑制滤波器的带陷效应带来的测量零值变化。理想的补偿滤波器其幅频响应与干扰抑制滤波器的关系如图 4所示。

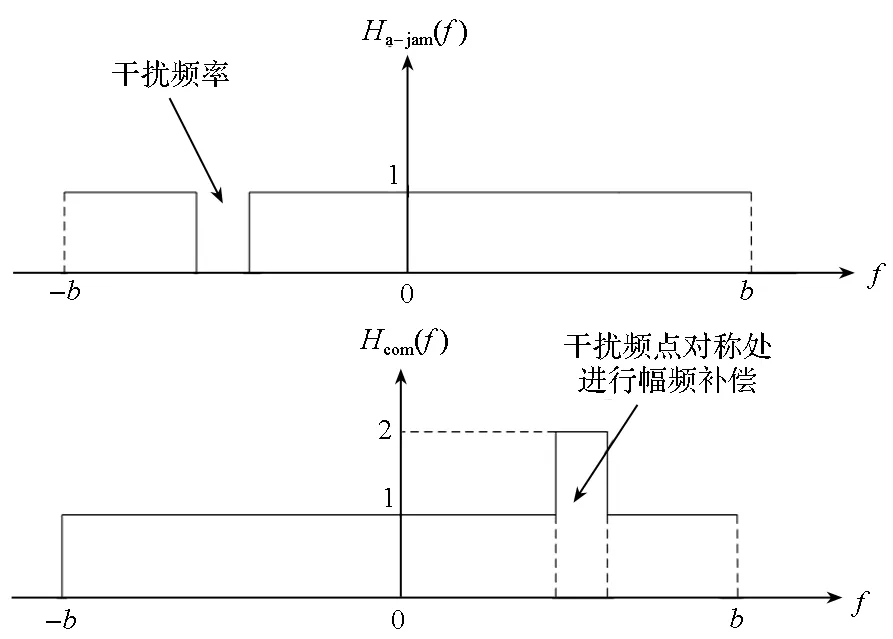
图4　理想的补偿滤波器与干扰抑制滤波器幅频响应的关系Fig.4　Ideal magnitude response of adaptive filter and compensation filter

双边抽头横向滤波器，单边抽头滤波器将本地PN码信号经过适当的延迟均可得到类似结论。由文献[4]可知，双边抽头横向滤波器的系数为：

(12)

其中N为滤波器阶数。由图4可知，补偿滤波器的幅频响应与干扰抑制滤波器的幅频响应的关系如式(13)所示。

Hcom(f)=2-Ha-jam(-f)

(13)

则为了满足式(13)，补偿滤波器的系数为：

(14)

则基于非理想信道下无偏的时域抗干扰滤波器的结构如图5所示。

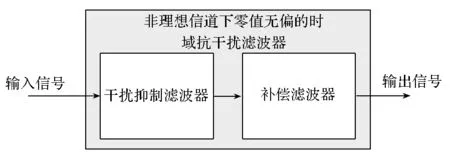
图5　非理想信道下零值无偏的时域抗干扰滤波器结构框图Fig.5　Structure of zero bias adaptive anti-jamming filter

3仿真验证

通过软件接收机比较零值无偏抗干扰滤波器与通道未校准的传统时域干扰抑制滤波器以及通道校准的传统时域干扰抑制滤波器三者的性能。仿真场景为不同干扰频率下的测量零值波动以及突发干扰情况下测量零值变化。传统的干扰抑制滤波器采用文献[4]介绍的最小均方误差准则设计。数字域的校准技术采用文献[8]介绍的方法，校准滤波器阶数为32。

场景一仿真参数如下：采样频率为65 MHz，伪码码率选择10.23 MHz，载噪比为35 dBHz，信号中频频率为20 MHz，干扰比为45 dBc，干扰带宽为1.023 MHz，干扰中频频率变化范围为10 MHz～30 MHz。模拟通道滤波器采用1.2节所示的模型，仿真中设定κ=1。自适应干扰抑制滤波器阶数为20。时延估计器采用相干早迟码结构，积分时间取10 ms，标准间隔取1，窄间隔取0.1。

仿真结果如图6和图7所示。由图6、图7可知，采用无偏的时域抗干扰滤波器，其在干扰频率发生变化时，测量零值波动很小，在0.2 ns以内。而传统的未经校准的干扰抑制滤波器测量零值波动幅度达到2 ns以上，经过通道校准后的测量零值波动幅度也达到了0.5 ns以上。

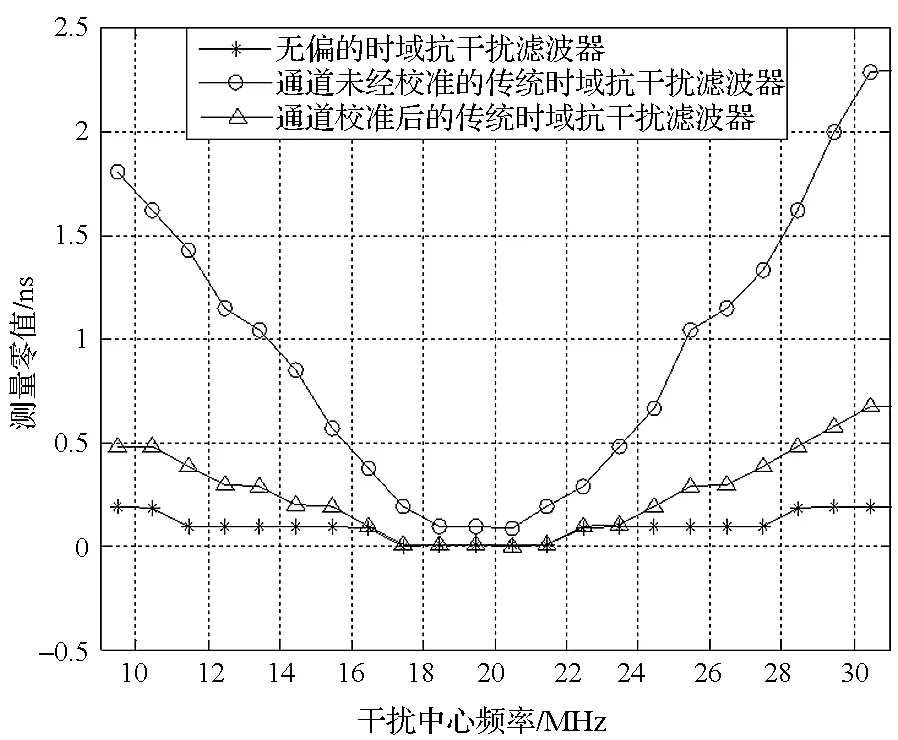
图6　相关器间隔为0.1个码片Fig.6　Correlator space is 0.1 chip

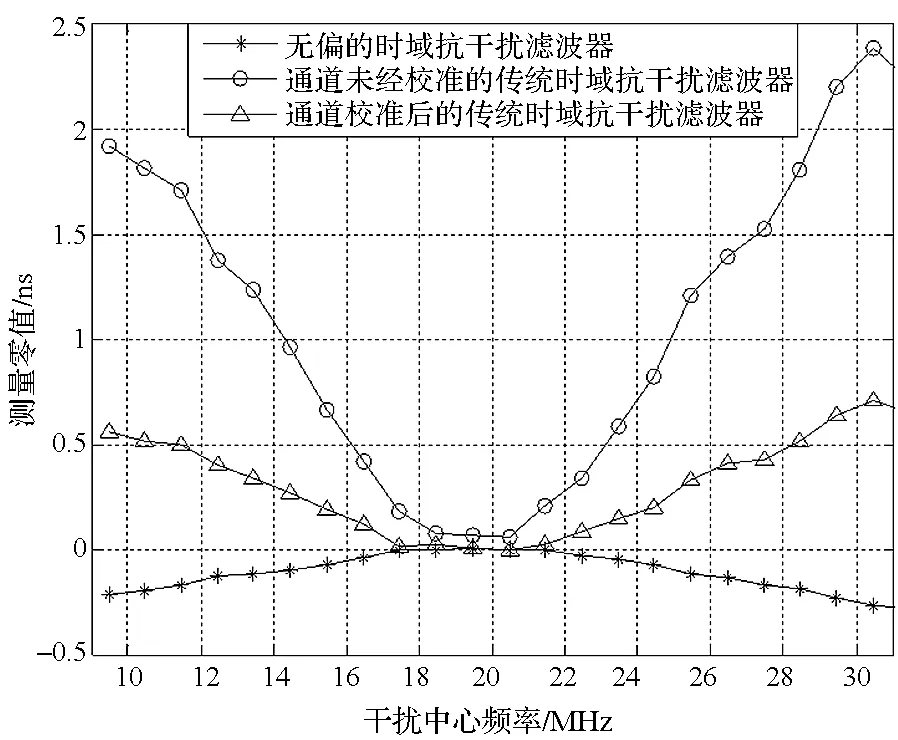
图7　相关器间隔为1个码片Fig.7　Correlator space is 1 chip

场景二仿真参数如下：信号参数和时延估计器的参数与场景一相同，相关器间隔为1个码片，在仿真的第4 s中突然加入窄带干扰，干扰比为45 dBc，干扰带宽为1.023 MHz，干扰中频频率为26 MHz。

仿真结果如图 8所示，由图8可知，当第4 s加入干扰后，使用传统的时域抗干扰算法不论是通道校准前还是通道校准后测量零值都发生了明显的变化，而采用无偏的时域抗干扰滤波器其测量零值在干扰加入前后没有发生明显的变化。

4结论

针对非理想信道抗干扰接收机，提出了一种测量零值无偏的干扰抑制滤波器算法。该算法利用了幅频响应函数A(f)和群时延函数τg(f)是偶函数的特性，对由于带陷效应引起的通道时延变化进行补偿。理论分析和仿真实验结果表明，在干扰频率发生变化时以及突发干扰时，补偿后的自适应干扰抑制滤波器测量零值变化在0.2 ns以内，优于传统的干扰抑制滤波器。

参考文献(References)

[1]Hegarty C J. GNSS signals—an overview[C]//Proceedings of IEEE International Frequency Control Symposium， 2012: 1-7.

[2]Rusu-Casandra A, Marghescu I, Lohan E S. Impact of narrow-band interference on unambiguous acquisition approaches in Galileo[C] //Proceedings of International Conference on Localization & GNSS, 2011: 127-132.

[3]Varshney N, Jain R C. An adaptive notch filter for narrow band interference removal [C] //Proceedings of the Nineteenth National Conference on Communications, 2013: 1-5.[4]聂俊伟. 卫星导航接收机时域自适应抗干扰算法研究与实现[D]. 长沙： 国防科学技术大学， 2007.NIE Junwei. Study and realization of the technology of time domain adaptive anti-jamming for satellite navigation receiver[D]. Changsha: National University of Defense Technology, 2007.(in Chinese)

[5]McGraw G A, Young S Y R, Reichenauer K. Evaluation of GPS anti-jam system effects on pseudorange and carrier phase measurements for precision approach and landing [C] //Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation，2004：2742-2751.

[6]McGraw G A, McDowell C, Young S Y R, et al. Assessment of GPS anti-jam system pseudorange and carrier phase measurement error effects [C]//Proceeding of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2005: 603-617.

[7]王峰， 傅有光， 孟兵， 等. 基于傅里叶变换的雷达通道均衡算法性能分析及改进[J]. 电子学报, 2006, 34(9): 1677-1680.WANG Feng, FU Youguang, MENG Bing, et al. Performance analysis and improvement of the equalization algorithm based on fourier transform for radar channel[J]. Acta Electronica Sinica, 2006, 34(9): 1677-1680. (in Chinese)[8]Sureka A K, Pupalaikis P J. Group delay compensation using IFFT filters: US20060195502[P]. 2006.

[9]Keegan R G, Knight J E. Signal receiver with group delay and amplitude distortion compensation: US8837654[P]. 2014.[10]李柏渝. 高性能卫星导航接收机模拟信道关键技术研究[D]. 长沙： 国防科学技术大学， 2011.

LI Baiyu. Study on key techniques of the analog signal channel in high performance satellite navigation receiver[D]. Changsha: National University of Defense Technology, 2011.(in Chinese)

[11]肖志斌. 高精度导航接收机的群时延建模、测量和校准技术[D]. 长沙： 国防科学技术大学， 2014.XIAO Zhibin. Group delay modeling，measurement and calibration technique for high accuracy navigation receiver[D]. Changsha: National University of Defense Technology, 2014.(in Chinese)

doi:10.11887/j.cn.201602021

*收稿日期：2015-12-26

基金项目：青年科学基金资助项目(61403413)

作者简介：范广腾(1988—)，男，安徽宣城人，博士研究生，E-mail:fanguangteng@163.com； 孙广富(通信作者)，男，研究员，博士，博士生导师，E-mail:gfsun@nudt.edu.cn

中图分类号：TN967.1

文献标志码：A

文章编号：1001-2486(2016)02-123-05

Zero bias anti-jamming filter design in non-ideal channel

FAN Guangteng, NI Shaojie, TANG Xiaomei, CHEN Huaming, SUN Guangfu

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：There is non-zero bias for the receiver due to the anti-jamming filter in non-ideal channel. Furthermore, since the tap weights of the adaptive transversal filter varies based on jamming pattern, the bias will also vary. This problem of code tracking bias has been a significant hurdle to achieving interference suppression capabilities in precision global navigation satellite system applications. Aiming at this problem, using the symmetrical characteristic of non-ideal analog receiver channel, a new technique called zero bias anti-jamming filter was presented. The proposed method could be easy implement in engineering. Theoretical analysis and simulative results show that the proposed method is capable of reducing the bias to less than 0.2 ns, which is significantly smaller than the traditional adaptive anti-jamming filter.

Key words：non-ideal channel; anti-jamming filter; zero bias; precision measurement

http://journal.nudt.edu.cn