高轨双星辐射源跟踪的高斯和-容积Kalman滤波算法*

李　曦，杨　乐,，郭福成，刘　洋，张　敏

(1.江南大学 物联网工程学院， 江苏 无锡　214122； 2.国防科技大学 电子科学与工程学院， 湖南 长沙　410073)



高轨双星辐射源跟踪的高斯和-容积Kalman滤波算法*

李曦1，杨乐1,2，郭福成2，刘洋2，张敏2

(1.江南大学 物联网工程学院， 江苏 无锡214122； 2.国防科技大学 电子科学与工程学院， 湖南 长沙410073)

摘要：针对辐射源运动方程和观测方程的强非线性，提出基于高斯和框架与5阶容积Kalman滤波(5CKF)的跟踪算法GS-5CKF。该方法将起始时刻的时差观测量所确定的位于地球表面的时差线按经度等间隔划分，初始化多个并行的5CKF，线性组合各滤波器的输出获得辐射源运动状态的估计。针对5CKF，提出新的非线性测度并引入滤波器分裂与合并，从而提高了跟踪精度，同时保持GS-5CKF算法复杂度基本不变。仿真表明，相对仅使用单个5CKF和基于高斯和框架但使用3阶容积Kalman滤波器的GS-3CKF等方法，提出的算法具有更高的估计精度。

关键词：高斯和；5阶容积Kalman滤波；辐射源跟踪；非线性滤波；分裂与合并

定位地球表面的运动辐射源具有重要的民用和军用价值。使用静止轨道(GEostationary Orbit, GEO)卫星实现辐射源的被动跟踪具有隐蔽性好、覆盖区域广、对同一片区域可连续监视等优点[1]。本文考虑使用两颗位于赤道上空的GEO卫星跟踪巡航状态的地面辐射源，辐射源载频已知且固定。高轨双星从辐射源信号中估计信号的到达时差(Time Difference Of Arrival, TDOA)、到达频差(Frequency Difference Of Arrival, FDOA)以及信号到达高轨卫星的多普勒频移(Doppler shift)，以跟踪辐射源的运动。上述问题是多种重要应用的抽象，如连续监视星下一定经纬度范围内(如北纬0°～40°，东经100°～140°)的无人机等飞行器。

已有的双站辐射源跟踪文献主要考虑了接收站与辐射源处于同一平面且相距数十千米的情形[2-3]，这时，仅使用信号的TDOA和FDOA观测量即可实现辐射源跟踪[2-3]。相比已有文献，本文研究的高轨双星辐射源跟踪是一个三维空间中的估计问题。另外，由于GEO卫星与辐射源距离较大(可达数万千米)，需引入辐射源信号到达卫星的多普勒频移等观测量，以提高运动参数(如辐射源位置和速度)的可观测性(observability)[4]。

值得指出的是：本文考虑的辐射源是非合作性的，其信号发射时间未知，故无法从其信号到达时间(Time Of Arrival, TOA)直接获得辐射源与卫星的距离信息。这使得在卫星导航系统中得到广泛应用的基于TOA的瞬时定位方法不再适用。

高轨双星辐射源跟踪问题是非线性的，其非线性主要来源于两个方面。首先，辐射源沿地球表面运动，其运动方程在大地 (geodetic) 坐标系和地心地固(Earth-Centered, Earth-Fixed, ECEF)坐标系下均是非线性的；其次，时差、频差以及辐射源信号到达卫星的多普勒频移等观测量与辐射源运动参数的函数关系也是非线性的。因此，需使用非线性滤波技术实现辐射源运动参数的在线(online)估计。

实际中广泛使用的非线性滤波器有扩展Kalman滤波器(Extended Kalman Filter, EKF)[5]、无迹Kalman滤波器(Unscented Kalman Filter, UKF)[6]、3阶容积Kalman滤波器(3rd-order Cubature Kalman Filter, 3CKF)[7]和Gauss Hermitian Kalman滤波器[8]等。它们使用高斯分布逼近状态矢量的后验概率密度。因高轨双星辐射源跟踪问题非线性较强，仅使用单个非线性滤波器难以获得较好的跟踪精度，滤波算法也容易发散。

近年提出的粒子滤波器(Particle Filter, PF)[9]是一种基于蒙特卡洛(Monte Carlo，MC)方法的非线性滤波器。PF能够处理非高斯、非线性滤波问题，且能够逼近任意后验概率密度函数。但PF计算量较大，且随着状态矢量维数的增加，所需粒子数量也急剧增多。

本文以新近提出的5阶容积Kalman滤波器(5th-order Cubature Kalman Filter, 5CKF)[10]为基础，提出了一种基于高斯和(Gaussian Sum, GS)框架以及5CKF的高轨双星辐射源跟踪算法GS-5CKF。GS-5CKF包含多个并行的5CKF；在每个采样时刻，融合所有5CKF的输出获得辐射源运动参数的估计。

GS-5CKF算法是文献[11]中针对仅测角跟踪(Bearing-Only Tracking, BOT)提出的基于GS框架和3CKF的GS-3CKF算法的扩展。与GS-3CKF不同的是：首先，GS-5CKF使用5CKF替代了GS-3CKF中的3CKF。这是因为高轨双星辐射源跟踪问题有较强的非线性，而5CKF在处理非线性滤波问题时具有更好的性能[10]。另外，针对 5CKF，本文提出新的非线性测度(nonlinearity measure)，度量每个5CKF状态更新运算的非线性程度。若某个5CKF的非线性测度高于预设的阈值，则将该滤波器分裂(splitting)，以降低状态更新运算的非线性程度，进一步提高估计精度。为保持GS-5CKF算法所包含的滤波器数量和复杂度基本不变，本文使用滤波器合并(merging)[12]以消除滤波器分裂带来的滤波器数量的增加。

GS-5CKF算法的初始化利用了由起始时刻的辐射源信号时差观测量所确定的在地球表面的时差线。将时差线按经度等间隔划分，使GS-5CKF所包含的多个5CKF的辐射源初始位置估计在时差线上较均匀地分布。

1问题描述

考虑图1所示的辐射源跟踪场景。

图1　高轨双星辐射源跟踪场景Fig.1　Source geolocation using dual GEO satellites

为简化讨论，假定地球为一个半径等于赤道半径的正球体[1]。上述近似在北纬0°～40°范围内引入了不超过10 km的密合误差，仿真表明上述近似误差对估计精度的影响不显著(见本文第3节)。辐射源沿地球表面做等高程巡航，其运动方程可写作：

(1)

状态转移矩阵Fk定义为：

其中：T是观测间隔；R=6378.137 km是赤道半径；H是辐射源高程，假设已知；Bk和Lk分别表示kT时刻(k=0,1,2,…)辐射源纬度和经度，单位为rad；VN,k和VE,k是kT时刻辐射源沿正北和正东方向的速度。

可以看出，状态转移矩阵Fk与(k-1)T时刻辐射源的纬度Bk-1有关，故辐射源运动方程是非线性的。式(1)中，mN,k和mE,k是过程噪声，反映了辐射源运动速度的随机变化；假设mN,k和mE,k是独立的零均值高斯白噪声。

令xk=[Bk,Lk,VN,k,VE,k]T为待估计的运动辐射源的状态矢量。需要指出的是，对辐射源高程变化的描述可通过在式(1)中增加高程和高程变化率两个状态变量实现。为简化讨论，本文仅考虑辐射源做等高程巡航的情形。

高轨双星系统测量辐射源信号的TDOA，FDOA以及信号到达主星s1,k的多普勒频移。在kT时刻，上述观测量分别记作：

(2)

(3)

(4)

其中，nΔr,k，nΔf,k和nfd,k是测量噪声，假设它们是独立的零均值高斯白噪声。时差观测量在数值上等于辐射源信号到达两颗卫星的到达时间的差。由于上述相减运算的引入，大气延迟等因素对于时差观测量的影响不显著。λ=c/fo是辐射源信号的波长(c=299 792 458 m/s是光速，fo为辐射源信号的载频，假设f0固定且已知)。uk和vk是kT时刻辐射源在ECEF坐标系下的位置和速度矢量，它们由辐射源的状态矢量xk经如式(5)、式(6)所示变换得出。

(5)

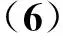
从式(2)～(4)可以看出，在每个采样时刻，高轨双星可获得关于辐射源状态矢量xk的三个观测量，考虑到xk含四个未知量，因此系统无法从当前时刻的观测矢量zk=[Δrk,Δfk,fdk]T中直接估计xk。

将辐射源运动模型式(1)和时差、频差以及主星多普勒频移的观测方程式(2)～(4)联立为如式(7)所示的离散时间状态空间(state-space)模型：

(7)

其中，mk=[0,0,mN,k,mE,k]T是过程噪声矢量，nk=[nΔr,k,nΔf,k,nfd,k]T是观测噪声矢量，它们是相互独立的零均值高斯白噪声，mk和nk的协方差矩阵分别记作Qk和Rk。

2辐射源跟踪算法

高轨双星辐射源跟踪算法GS-5CKF包含多个并行的5阶容积Kalman滤波器(5CKF)。在每个采样时刻，GS-5CKF更新各5CKF的权重，并计算5CKF输出的线性组合获得对运动辐射源状态矢量xk的估计。

2.1GS-5CKF算法

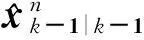
在kT时刻，GS-5CKF的每个5CKF首先进行状态预测(prediction)：

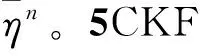
(8)

(9)

(10)

其中，

(11)

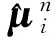
第n个5CKF的平均相对非线性度是：

(12)

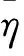
(13)

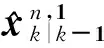
(14)

5CKF-Update{·}代表5CKF的状态更新运算，其流程将在2.2节给出。

(15)

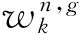
2.25阶容积Kalman滤波算法

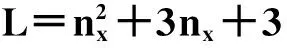
表1　5CKF的Sigma点及权重

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

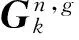
式中，Rk是观测噪声nk的协方差矩阵。对比文献[7]以及式(16)～(25)可以看出：5阶容积Kalman滤波器与3阶容积Kalman滤波器的状态预测和更新过程相似，主要的区别在于Sigma点的位置及其权重选择。

2.3GS-5CKF算法的初始化

非线性滤波算法的初始化对其估计性能有明显的影响；较大的初始化误差可导致滤波算法收敛慢、估计精度降低，甚至可能导致算法发散[15]。本文基于文献[2-3，15]提出的利用起始时刻的辐射源信号时差观测量初始化二维高斯和滤波算法的框架，发展出一种能初始化三维的跟踪算法GS-5CKF的方法。上述方法的关键在于计算由起始时刻的时差观测量确定的双曲面与地球表面的交线(即时差线)。

不失一般性，假设起始时刻是0时刻，该时刻的时差观测量是Δr0。若没有观测误差，Δr0可以确定一个双曲面，它是由Δr0给定的、焦点在0时刻主星和辅星位置(即s1,0和s2,0)的双曲线绕连接s1,0和s2,0的对称轴旋转而成；在0时刻，辐射源必然位于上述双曲面与距地球表面H的正球面相交形成的时差线上。这里，H是辐射源已知高程。

时差线的准确计算较为复杂。本文提出一种简便的近似计算方法。考虑到实际应用中，辐射源与双星的距离远大于双星间距，因此，由Δr0确定的双曲面可由一个正圆锥面近似，其顶点在s1,0和s2,0的中点，半顶角φ0为：

(26)

该正圆锥面是首先将由Δr0确定的、焦点在s1,0和s2,0位置的双曲线用其渐近线代替[16-17]，再绕连接s1,0和s2,0的对称轴旋转而成。由双曲面与距地球表面H的正球面相交而成的时差线可以由上述正圆锥面与距地球表面H的正球面相交所得的近似时差线逼近。

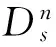
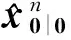
(27)

(28)

其中，

从式(27)和式(28)可以看出，在起始时刻，每个5CKF的辐射源运动速度估计值均设为0；辐射源位置估计值是不同位置误差椭圆的中心，它分布在由起始时刻的时差观测量确定的近似时差线上。

3仿真实验

考虑如下仿真场景：采样间隔T=45 s，跟踪总时长为45 min。辐射源信号的载频为fo=14 GHz。辐射源信号到达高轨双星系统的时差、频差以及到达主星的多普勒频移的观测误差的标准差分别等于0.1 μs，0.01 Hz和50 Hz。辐射源高程等于18 km，其巡航速度为150 m/s，航向正东。在跟踪起始时刻，辐射源位于北纬25°，东经119.7°。

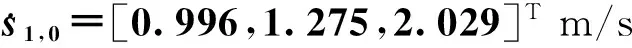
仿真实验使用GS-5CKF和GS-3CKF[11]两种算法实现对运动辐射源的跟踪。为确保比较的公平性，本文使用2.3节提出的初始化方法同时初始化GS-5CKF和GS-3CKF。另外，两种算法分别包含30个5CKF和30个3CKF；且均假设辐射源高程为10 km，与真实辐射源高程存在8 km的误差。仿真实验表明，仅使用30个容积Kalman滤波器，GS-5CKF和GS-3CKF就能获得较好的辐射源跟踪精度；高程误差对定位估计精度的影响也不显著。

根据文献[11], 本文设定GS-5CKF和GS-3CKF的辐射源运动速度的随机噪声的标准差为10-3m/s。值得指出的是，该标准差的选择会影响滤波算法的噪声抑制和跟踪能力。为进一步提升GS-5CKF算法的实用性，在未来的工作中可考虑引入运动速度随机噪声方差在线估计[18]或交互多模型(Interactive Multiple Model, IMM)等技术。非线性度的阈值γ设定为0.2。另外，仿真假定如下的先验信息是已知的：辐射源位于北半球，其位置的纬度范围是0°到40°；其最大速度为Vmax=250 m/s。

图2给出了在某一次蒙特卡洛仿真中，使用2.3节提出的初始化方法获得的30个辐射源位置估计(图中用三角形表示)及其误差椭圆。从图中可以看出，因近似时差线按照辐射源位置经度等间隔分割，获得的30个辐射源位置估计较均匀地分布在由跟踪起始时刻的时差观测量确定的近似时差线上，且不同的误差椭圆的面积也相似。

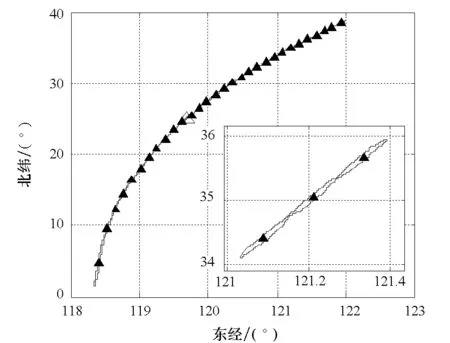
图2　由跟踪起始时刻的时差观测量近似确定的辐射源位置估计及其误差椭圆Fig.2　Source location estimates and the associated error ellipses derived from the TDOA measurement obtained at the beginning of the source tracking process

图3和图4给出了在1000次蒙特卡洛仿真中GS-5CKF和GS-3CKF算法对辐射源位置与速度估计的均方根误差(Root Mean Square Error, RMSE)。另外，两个图中还包含了辐射源位置和速度估计的克莱默-劳下界(Cramer-Rao Lower Bound, CRLB)以及GS-5CKF的第14个5CKF单独运行时(不进行滤波器分裂和合并操作)对辐射源的位置和速度的估计RMSE。在起始时刻，第14个5CKF的辐射源位置估计误差为247 km。

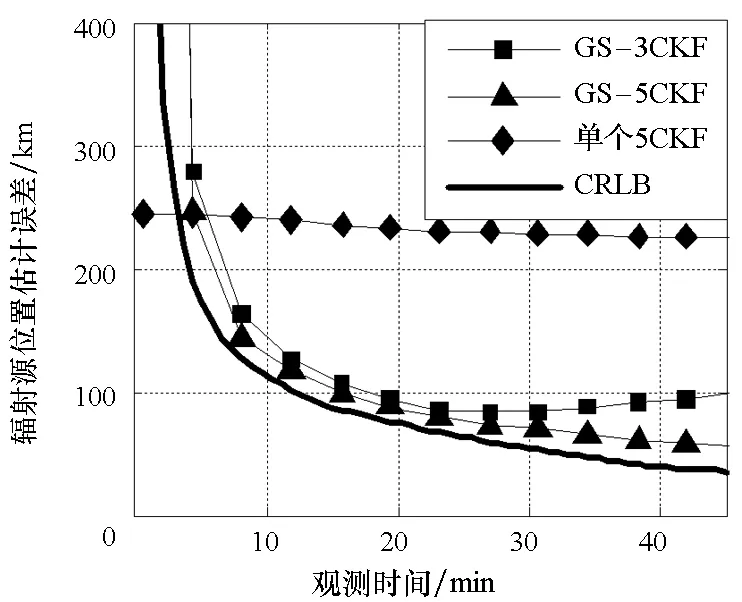
图3　位置估计RMSEFig.3　Position estimation RMSE

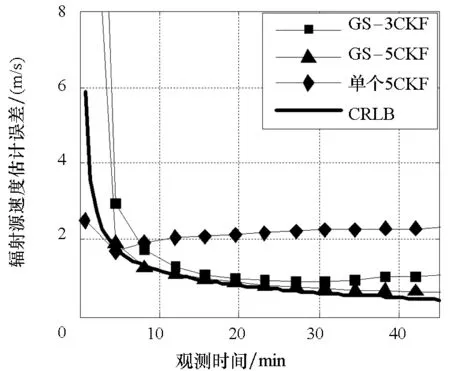
图4　速度估计RMSEFig.4　Velocity estimation RMSE

从图3和图4可以看出，由于高轨双星辐射源跟踪问题较强的非线性，在辐射源位置初始化存在一定误差的情况下，仅使用单个5CKF并不能获得较好的辐射源位置和速度估计精度；随着跟踪时间的增加，单个5CKF的估计RMSE曲线并未出现明显的下降。

另外，从图3和图4中可知，相对于单个5CKF，GS-5CKF和GS-3CKF算法的估计RMSE随着观测量的积累迅速下降，两种方法的收敛速度接近。由于5CKF的使用，GS-5CKF比GS-3CKF有着更高的估计精度，其性能更接近CRLB。以图3为例，在第40 min，GS-5CKF的辐射源位置估计RMSE比GS-3CKF的要低近30 km。

图5给出了在上述1000次蒙特卡洛仿真中，GS-5CKF算法各5CKF的相对非线性度的平均值随时间变化，以反映滤波器分裂和合并操作对算法估计性能的影响。从图中可知，在跟踪起始阶段，各5CKF的位置估计协方差矩阵与时差线基本重合(如图2所示)，各5CKF的相对非线性度均较低。随着滤波的进行，各5CKF的相对非线性度显著上升，滤波器分裂和合并操作频繁发生，降低了5CKF的状态更新运算的非线性程度，有效地提升了GS-5CKF算法的估计精度(对比图3和图4)。在本仿真中，第20 min后，参与分裂与合并的滤波器数量减少，这是因为多数5CKF的状态矢量协方差矩阵已较小。

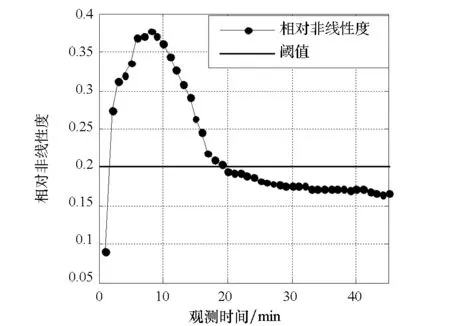
图5　相对非线性度的平均值随时间的变化Fig.5　Temporal evolution of the averaged relative nonlinearity measure

4结论

针对非线性的高轨双星辐射源跟踪问题，提出基于高斯和框架与5阶容积Kalman滤波器的GS-5CKF滤波算法。针对5CKF，提出了新的非线性测度，并引入了滤波器分裂和合并操作，以提升GS-5CKF算法的性能并保持算法的计算复杂度不变。GS-5CKF算法的初始化通过计算由跟踪起始时刻的辐射源信号时差观测量近似确定的正圆锥面与地球表面相交而成的时差线实现。仿真表明，对于高轨双星辐射源跟踪问题，在初始化误差较大时，单个非线性滤波器(如单个5CKF)难以获得较好的跟踪性能，而GS-5CKF的估计精度随着观测量的累积迅速提高。相对于文献中已有的基于高斯和框架与3阶容积Kalman滤波器的GS-3CKF算法，GS-5CKF有着更高的估计精度，其估计性能更接近CRLB。

参考文献(References)

[1]Ho K C, Chan Y T. Geolocation of a known altitude object from TDOA and FDOA measurements [J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 770-783.

[2]Musicki D, Kaune R, Koch W. Mobileemitter geolocation and tracking using TDOA and FDOA measurements [J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1863-1874.

[3]Musicki D, Koch W. Geolocation using TDOA and FDOA measurements [C]//Proceedings of 11th International Conference on Information Fusion (FUSION), 2008: 1-8.

[4]Deng B, Xiong J Y, Xia C X. The observability analysis of aerial moving target location based on dual-satellite geolocation system [C] //Proceedings of International Conference on Computer Science and Information Processing (CISP), 2012: 12-15.

[5]Jazwinski A H. Stochastic processing and filtering theory[M]. New York: Academic Press, 1970.

[6]Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation [J]//Proceedings of the IEEE, 2004, 92(3): 401-422.

[7]Arasaratnam I, Haykin S. Cubature Kalman filters [J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[8]Sarkka S. Bayesian filtering and smoothing [M]. New York: Cambridge University Press, 2013.

[9]Arulampalam M S, Maskell S, Gordon N, et al. Atutorial on particle filter for on-line non-linear/non-Gaussian Bayesian tracking [J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188.

[10]Wang S, Feng J, Tse C K. Spherical simplex-radial cubature Kalman filter [J]. IEEE Signal Processing Letters, 2014, 21(1): 43-46.

[11]Leong P H, Arulampalam S, Lamahewa T A, et al. A Gaussian-sum based cubature Kalman filter for bearings-only tracking [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1161-1176.

[12]Crouse D F, Willett P, Pattipati K, et al. A look at Gaussian mixture reduction algorithms[C]//Proceedings of 14th International Conference on Information Fusion (FUSION), 2011: 1-8.

[13]Faubel F, Klakow D. Further improvement of the adaptive level of detail transform: splitting in direction of the nonlinearity[C]//Proceedings of 18th European Signal Processing Conference (EUSIPCO), 2010: 850-854.

[14]Faubel F, Klakow D. An adaptive level of detail approach to nonlinear estimation[C] //Proceedings of International Conference on Acoustics Speech and Signal Processing (ICASSP), 2010: 3958-3961.

[15]Daun M, Kaune R. Gaussian mixture initialization in passive tracking applications[C] //Proceedings of 13th International Conference on Information Fusion(FUSION), 2010: 1-8.

[16]Drake S R, Dogancay K. Geolocation by time difference of arrival using hyperbolic asymptotes[C] //Proceedings of International Conference on Acoustics Speech and Signal Processing (ICASSP), 2004, 2: 361-364.

[17]Dogancay K. Emitter localization using clustering-based bearing association[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(2): 525-536.

[18]Lee D J. Nonlinear Bayesian filtering with applications to estimation and navigation[D] Thesis: Texas A & M University, 2005.

doi:10.11887/j.cn.201602017

*收稿日期：2015-04-16

基金项目：国家自然科学基金青年科学基金资助项目(61304264，61305017)；江苏省自然科学基金资助项目(BK20140166)

作者简介：李曦(1990—)，男，江苏南京人，博士研究生，E-mail: lx_njgc@163.com;杨乐(通信作者)，男，副教授，博士，硕士生导师，E-mail: le.yang.le@gmail.com

中图分类号：TN971

文献标志码：A

文章编号：1001-2486(2016)02-099-08

Gaussian-sum based cubature Kalman filtering algorithm for source geolocation using dual geostationary satellites

LI Xi1, YANG Le1,2, GUO Fucheng2, LIU Yang2, ZHANG Min2

(1. School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China;2. School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：To tackle the inherent high nonlinearity of motion equation and observation equation of radiation source, a GS (Gaussian-sum) based 5CKF (5th-order cubature Kalman filter) tracking algorithm, referred to as GS-5CKF, was proposed. It consists of multiple parallel 5CKFs, which were initialized through partitioning the candidate source positions determined by the time difference of arrival measurement at the beginning of the tracking process with respect to the source latitude. The linear combination of filter outputs was conducted to estimate the motion state of radiation source. A new nonlinearity measure was advocated, on the basis of which a filtering splitting and merging procedure was developed to further enhance the performance of GS-5CKF while keeping its computational complexity fixed. Simulation results show that: compared with the tracking algorithms using the single 5CKF and the GS-3CKF, the newly proposed GS-5CKF technique exhibits higher source geolocation accuracy.

Key words：Gaussian sum; 5th-order cubature Kalman filtering; source tracking; nonlinear filtering; splitting and merging

http://journal.nudt.edu.cn