引入区域量化的相控阵天线维修优化模型*
王永攀,杨江平,张 宇,李陆军,3
(1. 空军预警学院 陆基预警装备系, 湖北 武汉 430019;2. 湖北工业大学 电气与电子工程学院, 湖北 武汉 430068;3. 中国人民解放军93975部队, 新疆 乌鲁木齐 830000)
引入区域量化的相控阵天线维修优化模型*
王永攀1,杨江平1,张宇2,李陆军1,3
(1. 空军预警学院 陆基预警装备系, 湖北 武汉430019;2. 湖北工业大学 电气与电子工程学院, 湖北 武汉430068;3. 中国人民解放军93975部队, 新疆 乌鲁木齐830000)
摘要:针对大型相控阵天线维修成本高、多部件维修时机难以确定、模型仿真计算困难等问题,提出一种引入区域量化的维修优化模型。建立天线阵列的区域量化模型,将天线阵列维修问题转化成一个由不同区域阵元组成的k/n系统维修优化问题。以使用可用度为约束条件,以单位时间维修费用最小为优化目标,建立引入区域量化的大型相控阵天线多部件视情维修决策优化模型,并通过算例仿真与分析进行了模型验证。结果表明:提出的维修优化模型真实有效,能够很好地解决分布不均匀的相控阵天线维修优化问题。
关键词:区域量化;维修优化模型;相控阵天线;阵元;直线阵
相控阵天线作为相控阵雷达作战技术性能的关键部分,通常要求停机维修的次数少、时间短、费用低[1]。然而,当前部队针对大型相控阵天线维修的情况却不容乐观,呈现出维修成本高、维修时机难以确定等问题。因此,如何在低维修成本的条件下确定大型相控阵天线的维修时机是一个亟待研究的课题。
由于相控阵天线由大量的天线单元组成,传统的单部件事后维修策略会增加系统的停机时间以及维修工作量,已很难适用于相控阵天线的维修。考虑到相控阵天线的冗余设计,部分学者将相控阵天线的维修问题看作一个由多个相同单元组成的k/n系统的维修[2-3]。在此基础上,文献[4-5]分别研究了大型相控阵雷达天线阵面的视情维修与定时维修策略,在一定程度上解决了相控阵天线的维修优化问题。然而,在工程设计中,为了得到较低的副瓣电平,天线阵列往往采用激励幅度加权的方式进行设计,从而导致处于不同位置的阵元对天线性能的影响不同,使得天线阵列的分布具有不均匀性[6]。因此,天线阵列应该是一个由不同单元组成的大型k/n系统。但是天线阵列阵元数目众多,使得天线维修优化建模的仿真计算困难,难以进行工程应用。为了解决上述问题,可以首先根据阵元对天线性能的影响对天线阵列进行区域量化,进而将不同单元组成的大型k/n系统的维修优化问题转化成一个由不同区域单元组成的k/n系统的维修优化问题,从而简化运算,以便进行工程运用。
为了研究天线阵元失效与天线性能之间的关系,部分专家学者开始用设计密度加权阵的思想来分析阵元失效问题,出现了一些研究成果[7-9]。然而这些文献认为处于不同位置的阵元对天线性能的影响是相同的,因此只研究了阵元失效率对天线性能的影响,并没有研究不同位置的阵元失效对天线性能的影响。但是在实际运用中,对于采用幅度加权的天线阵列,不同位置的阵元失效对天线性能的影响是不同的,因此,研究不同位置的阵元失效对天线性能的影响,总结阵元失效对天线性能的影响规律是进行天线阵列区域量化的基础。
1阵元失效影响分析
1.1阵元失效影响模型
假设天线阵列由N个阵元组成,天线阵元各向同性,且以间隔d均匀排列在一条直线上。则以第一个阵元为坐标原点可建立如图1所示坐标系。记处于第n个位置的阵元为A(n),其中n=1,2,…,N。
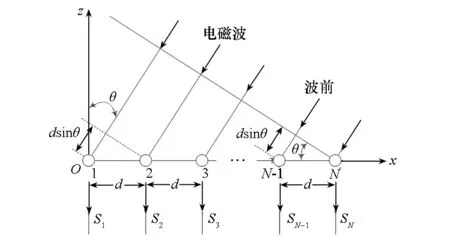
图1 N元直线阵Fig.1 Linear antenna with N array element
由于天线阵元各向同性,即阵元因子Se(θ)=1,则N元直线阵的天线方向图[10]为:
(1)
其中:k为波数,k=2π/λ,λ为波长;In为第n个阵元的幅度值,采用Taylor加权。
定义示性函数X(n),其中n=1,2,…,N。当A(n)正常工作时,记X(n)=1;当A(n)失效时,记X(n)=0。由此,得到N个阵元工作状态的示性矩阵X。进一步可得到关于A(n)工作状态的N元线性阵列方向图函数,即阵元失效影响模型。
(2)
影响相控阵雷达性能的参数有很多,其中天线增益、副瓣电平是两个非常重要的参数[11]。为此,主要考虑阵元失效对天线增益和副瓣电平的影响。
1.2阵元失效对天线增益的影响
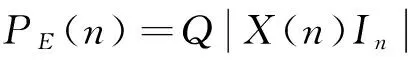
(3)
根据增益的定义,阵元失效时在最大的波瓣方向θ0的天线增益为:
(4)
当阵列中所有部件都完好时有X(n)=1,此时阵列增益G0(θ)最大。
(5)
得到天线增益的下降率α为:
(6)
假设阵元数目为300,利用MATLAB进行仿真得到阵元失效对天线增益的影响关系如图2所示。从图2可以看出:不同位置的阵元单独失效时天线增益的下降率不到0.5%,表明天线增益变化不大;失效阵元的数目增大时,天线增益的下降率逐渐增加,表明天线增益变化剧烈,当天线阵元全部失效时,天线增益为0。
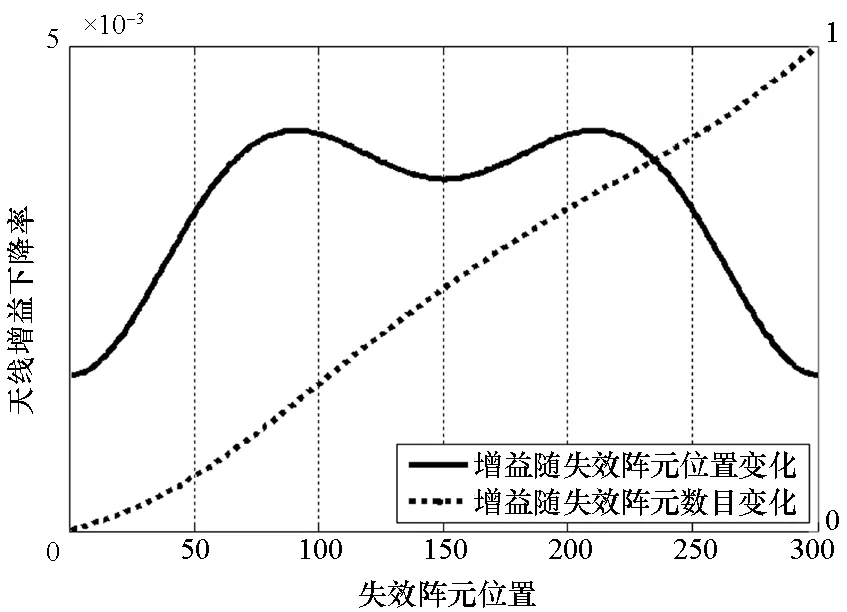
图2 阵元失效对天线增益的影响Fig.2 Influence from failure array element to gain of antenna
1.3阵元失效对副瓣电平的影响
根据建立的阵元失效影响模型,可通过仿真的方法研究阵元失效对副瓣电平的影响,总结阵元失效对副瓣电平的影响规律。
假设天线阵列由300个天线单元组成,其理想副瓣电平为-35 dB,阵元激励幅度服从Taylor分布。根据建立的阵元失效影响模型,通过MATLAB软件仿真,得到如图3所示的仿真结果。
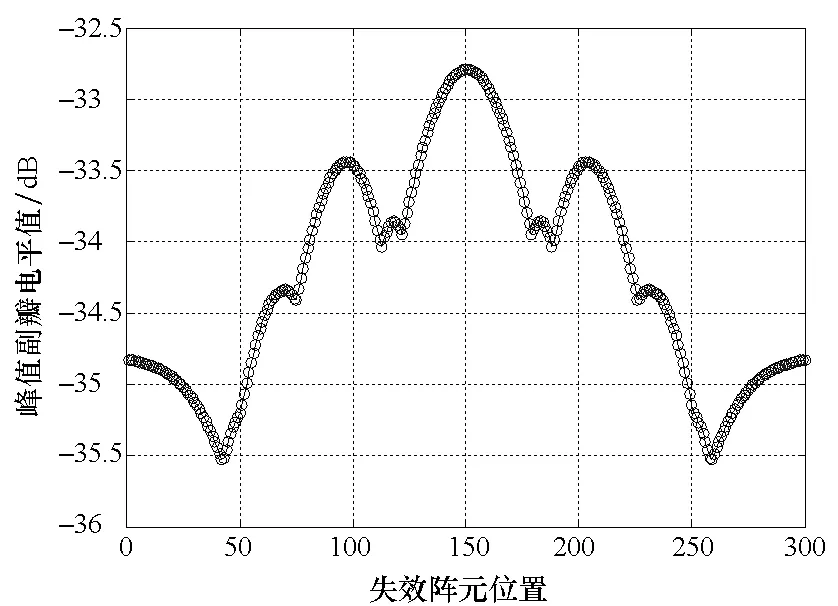
图3 不同位置阵元对副瓣电平的影响Fig.3 Influence from array element in different location to sidelobe level
从图3可以看出:关于阵列中心对称的阵元对副瓣电平的影响基本相同;并且在一定的副瓣电平变化范围内,阵元对副瓣电平的影响基本相同。由于阵元数目庞大,单个阵元对副瓣电平的影响较小,但是由于相控阵雷达对于天线低副瓣要求很高,因此研究不同位置阵元失效对天线副瓣电平的影响显得非常必要。
2天线阵列区域量化模型
通过上述分析可知,天线阵元对天线性能的影响随着阵元位置以及阵元数目的变化而不同,但是存在一定的阵元失效范围(记为区域Ri),在该范围内不同位置的阵元失效对天线性能的影响是基本相同的。此影响规律可以拓展到任意阵元数目的天线阵列,因此,大型天线阵列可以分割成多个不同的Ri,如图4所示。
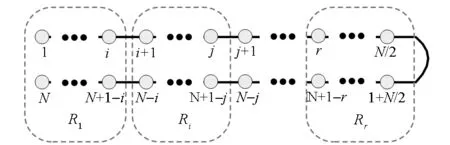
图4 天线阵列区域量化示意图Fig.4 Sketch of regional quantification of antenna array
定义确定区域Ri的过程为区域量化。进行区域量化以后,不同Ri内的阵元失效对天线副瓣电平的影响不同,而同一区域内的所有阵元对天线副瓣电平的影响相同。通过确定不同的Ri(i=1,2,…)就可以将系统变换为一个由多个不同区域阵元组成的k/n系统,进而为研究天线阵列的维修优化奠定基础。
2.1区域量化准则
区域量化准则主要根据不同位置的阵元单独失效时天线副瓣电平的变化进行确定。根据分析,可建立如下量化原则:
1)同一区域Ri内不同位置的阵元单独失效时,天线副瓣电平的变化范围不超过ΔB;
2)不同区域Ri和Rj之间无交集,所有区域Ri内阵元的数目的总和为整个天线阵列中阵元的数目。
2.2区域量化模型
根据区域量化的原则,建立天线阵列区域量化模型,如图5所示。区域量化模型分为数据处理和区域量化模型算法两个阶段。图5给出了主要符号的具体含义,下面简要分析该模型。
2.2.1数据处理阶段
步骤1:确定天线阵元的数目N以及区域量化等级level;
步骤2:根据第1.1节建立的阵元失效影响模型,计算每个阵元A(n)失效时天线的峰值副瓣电平PSLL(n);
步骤3:构建每个阵元失效时天线的峰值副瓣电平数据库PSLL,该数据库包含N个数据;
步骤4:计算所有峰值副瓣电平中的最大值Max与最小值Min;
步骤5:根据用户需求,确定区域量化范围内的副瓣电平变化值ΔB。
2.2.2区域量化模型算法
区域量化模型算法主要是借助数据处理得到的数据,逐个搜索阵元A(n)失效时天线的峰值副瓣电平PSLL(n)所在的范围,从而最终确定阵元A(n)所属的区域,具体算法流程如图5所示。
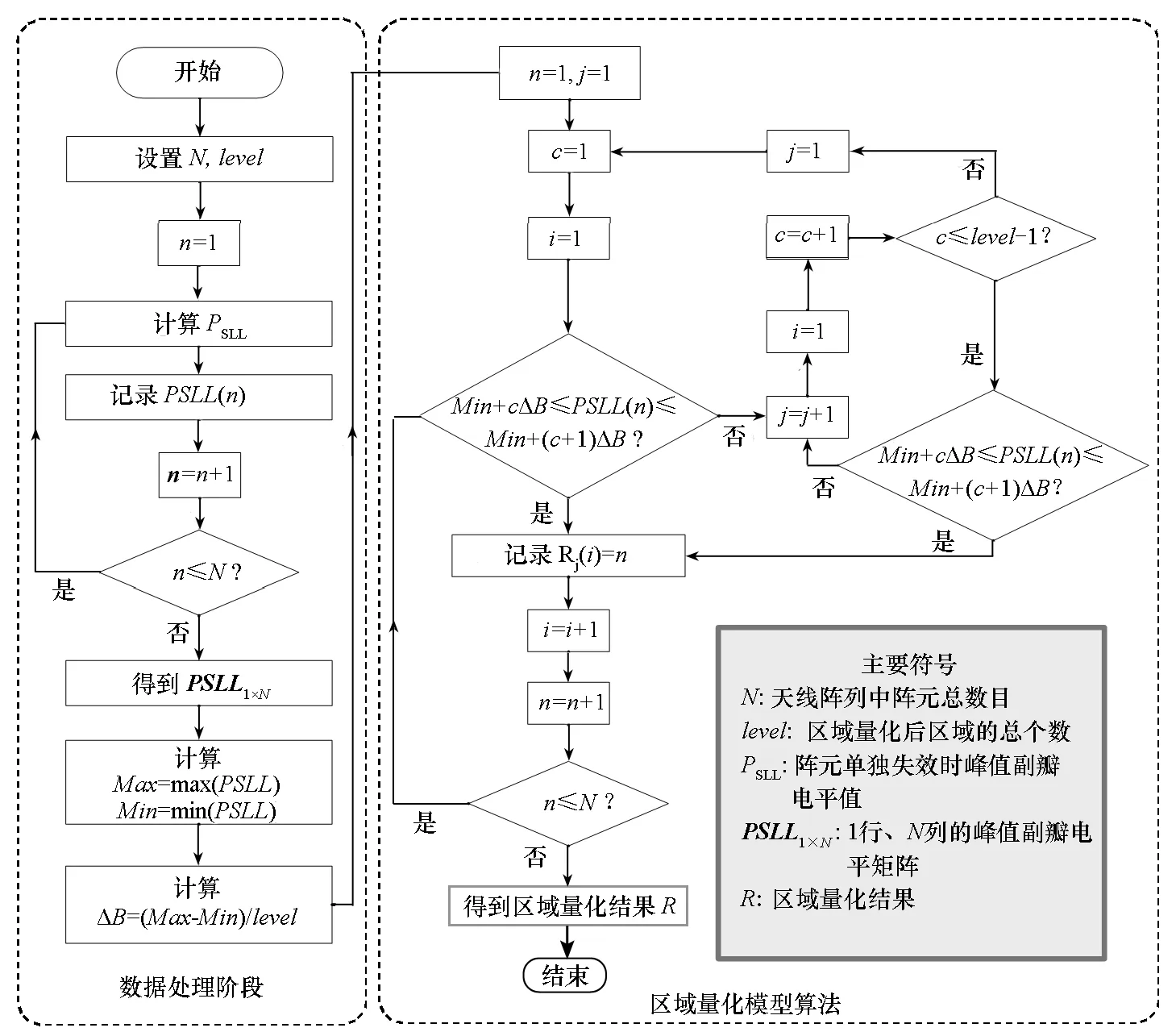
图5 直线型相控阵天线区域量化模型Fig.5 Regional quantification model of linear phased array radar antenna
2.3区域量化等级确定
要进行天线阵列的区域量化,首先要确定量化的等级level,即量化区域的个数。进行区域量化的目的是为了将天线阵列划分成多个不同的区域,以便于进行科学维修。设天线故障时故障阵元数目为m,则区域Ri应具备mk个故障阵元的容量。因此,在进行天线区域量化时,量化等级level的确定要保证区域Ri内阵元数目ni≥m。根据天线故障阵元与天线增益的关系可以确定level的值。一般认为天线增益下降率αi大于10%时,天线不能正常工作,若此时故障阵元数目为mk,则区域量化后Ri内阵元数目ni≥mk。图6给出了量化等级的确定方法。
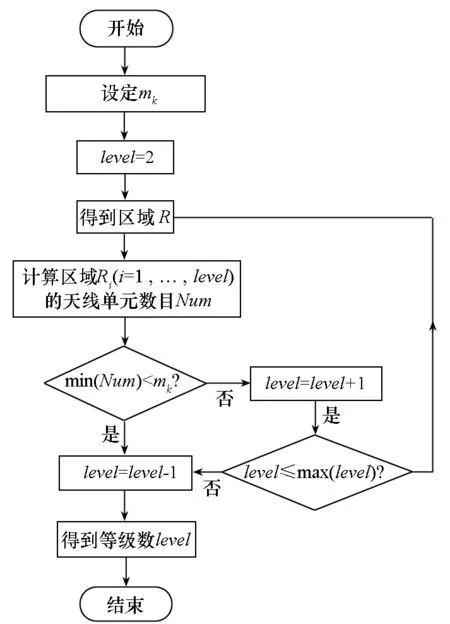
图6 区域量化等级确定方法Fig.6 Method to decide regional quantification level
3基于区域量化的维修优化模型
3.1维修优化模型
由于天线阵元幅度加权产生的电应力作用,不同区域内存在一定的故障权值,称为区域故障权值。因此,区域故障权值wλi与激励幅度IRi存在一定的函数关系。
wλi=f(IRi)
(7)
根据区域划分结果可求得区域Ri内阵元的平均激励幅度为:
IRi=∑Imni/Numi
(8)
其中,∑Imni为区域Ri内Numi个阵元的激励幅度之和。设阵元本身故障率为λ0,则可得区域Ri内的阵元故障率为:
λi=wλiλ0
(9)
因此,经过区域量化以后,天线阵列转换成由故障率为λi(i=1,2,…,level)的多个区域性阵元组成的k/n系统。进而,天线阵列的维修转换成不同单元组成的k/n系统的维修。
根据区域Ri内阵元的故障率可知区域Ri内阵元可靠度为:
Ri(t)=exp(-λit)
(10)
设区域Ri内阵元数目为Ni,则所有阵元正常工作时系统的可靠度为:
(11)
已知N个相互独立的不同元件组成的k/n系统中恰有m个元件发生故障的概率[13]为:
(12)
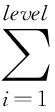
(13)
其中:NL为天线阵列中出现m个故障阵元的所有可能总数。
(14)
易知当N数目较大时,NL数目极大,运算复杂。当N为200时,m为40时,使用计算机已难以计算。为了简化运算量,设区域Ri出现mi个故障阵元的所有可能有NNL种,则式(13)可转化为:
(15)
进一步求得整个天线阵列的可靠度[14-15]为:
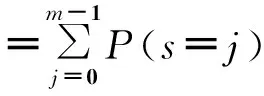
(16)
其中:
(17)
则其平均工作时间为:
(18)
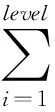
(19)
进而可求得天线阵列预防性维修的使用可用度A[16]为:
(20)
在满足装备使用可用度要求的条件下实现系统维修费用的最小化一直是部队追求的装备维修优化工作的最终目标。为此,系统的视情维修优化模型为:
(21)
其中:Ci为维修启动费用,元;Cr为维修人员的成本,元/(h·人);Cs为维修备件的储存与折旧费用,元/个;Ao为最低使用可用度要求。
3.2模型求解算法
3.2.1建立故障数据库
根据区域划分原则,每个区域Ri内具备mk个故障阵元的容量。天线阵列故障阵元达到mk时,认为天线失效需进行维修,因此,每个区域内故障阵元的数目mi应满足:
(22)
当有m个阵元失效时对天线阵列进行维修,假设关于每个区域出现mi个故障阵元的可能有NNL种。则第l(l=1,2,…,NNL)种失效状态下不同区域内天线阵元失效数目的矩阵Ml为:
Ml=[m1,m2,…,mlevel](1×level)
(23)
则天线阵列区域阵元失效数目矩阵为:
(24)
即为需要建立的故障数据库。
3.2.2具体算法流程
为了得到天线阵列的视情维修优化结果,结合上述分析,设计了图7所示的模型求解算法。通过MATLAB工具,输入相应的参数即可求得基于区域量化的相控阵天线维修优化结果。
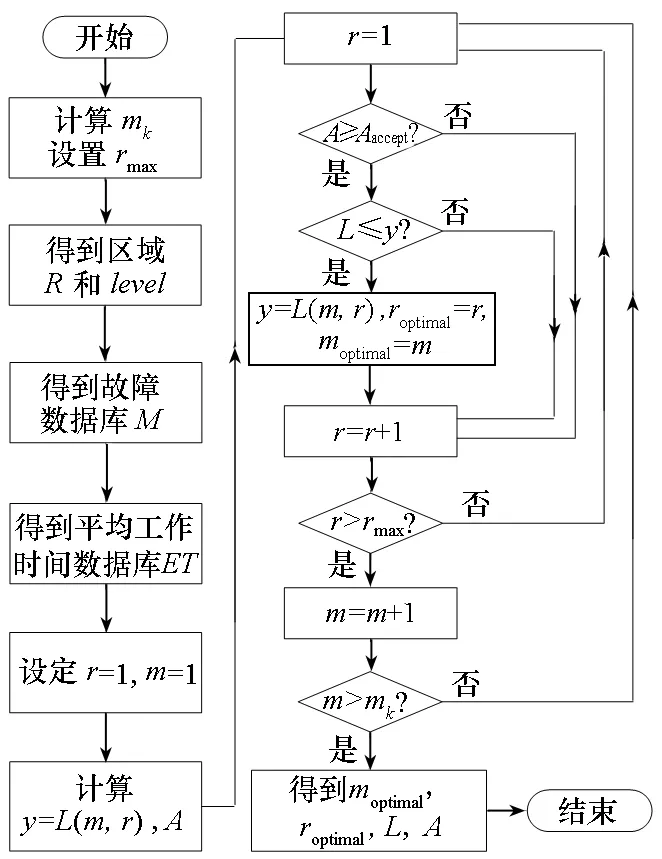
图7 模型求解算法Fig.7 Model solution algorithm
4算例仿真与分析
4.1天线阵列区域量化
已知某直线型相控阵天线由300个阵元组成,其理想副瓣电平为-35 dB,阵元激励幅度服从Taylor分布。根据区域量化模型及区域量化等级确定方法,借助MATLAB进行仿真,得到天线阵列的区域量化结果,如图8所示。从图8可以看出,天线阵列被划分成4个区域,不同的区域之间无交集,且阵元数目总和为天线阵元总数。
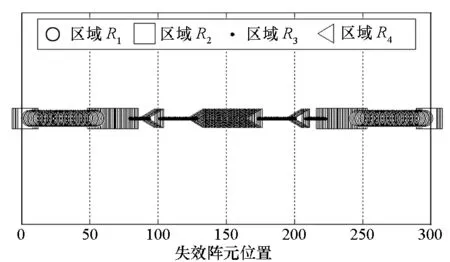
图8 天线阵列区域量化结果Fig.8 Regional quantification results of antenna array
表1给出了区域量化的具体结果,根据该区域量化结果,后续可以对量化的区域进行ki/ni系统的划分,为进一步指导天线阵列的维修提供科学、合理的理论依据。

表1 区域量化结果
4.2基于区域量化的维修优化
在对4.1节中的天线进行区域量化以后,做出如下假设:该雷达天线阵列阵元的正常寿命服从参数λ=0.000 5 次/h的指数分布,阵元的换件维修率μ=0.1个/h;启动一次换件维修所需费用Ci=20 000元;维修备件的储存与折旧费用Cs=5元/h;人均维修工时费Cr=20元;对维修后天线使用可用度的最低要求Ao=0.95;区域故障权值ωλi=IRi。试求在满足最低使用可用度要求下使得维修费用L最低的系统维修策略。
根据建立的区域量化模型及维修优化模型,将上述参数代入相应的模型,通过MATLAB进行仿真计算,可求得天线阵列的最佳视情维修阈值mopt=45个;最佳换件维修人数ropt=2;单位时间维修费用为L=270元/h;系统的使用可用度Ao=0.950 2,满足最低使用可用度要求。
图9给出了在维修人数ropt=2时单位时间维修费用与系统视情维修阈值的变化曲线。
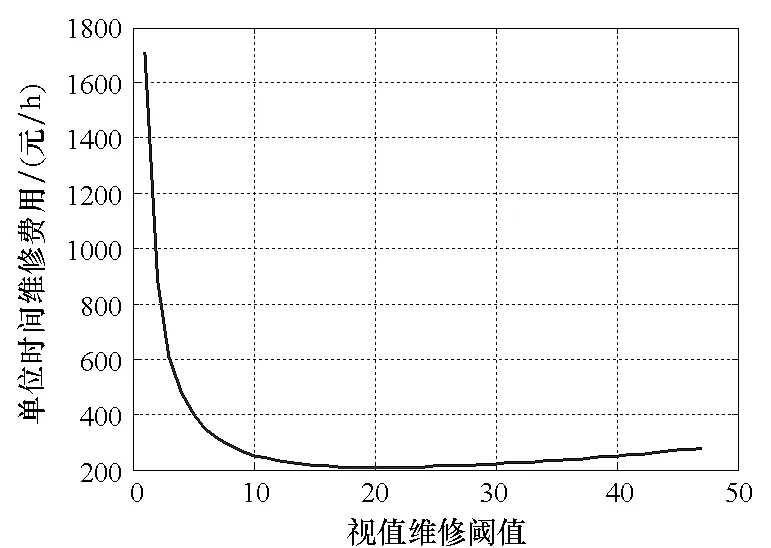
图9 单位时间维修费用曲线Fig.9 Maintenance cost curve of unit time
5结论
通过建立基于区域量化的维修优化模型,解决了阵面分布不均匀的相控阵天线维修优化建模中的计算困难、工程应用性差等问题,为进行科学、合理的相控阵天线维修提供了理论依据。总的来说,主要开展了以下工作:
1)建立了天线阵元的失效影响模型,通过理论推导与仿真分析的方法,分析了阵元失效对天线性能的影响规律;
2)提出了天线阵列区域量化的概念,并建立了天线阵列的区域量化模型。通过模型仿真可知,可以将天线阵列划分成不同的阵列区域,为进一步指导相控阵天线的维修提供了理论依据。
3)在天线区域量化的基础上,建立了基于区域量化的相控阵天线维修优化模型。通过该模型,可以在满足天线最低使用可用度的条件下使得维修费用最低,并且简化了运算量,方便工程应用。
4)对提出的天线阵列的区域量化模型和维修优化模型进行了算例仿真与分析。仿真和分析结果表明了提出的模型的正确性与可行性。
参考文献(References)
[1]李玮. 相控阵天线故障诊断方法研究与软件实现 [D]. 成都: 电子科技大学, 2014.
LI Wei. Research on fault diagnosis methods and software implementation for phased array antenna [D]. Chengdu: University of Electronic Science and Technology of China, 2014. (in Chinese)
[2]De Smidt-Destombes K S, Van der Heijden M C, Van Harten A. On the availability of a k-out-of-n system given limited spares and repair capacity under a condition based maintenance strategy [J]. Reliability Engineer-ing and System Safety, 2004, 83(3): 287-300.
[3]De Smidt-Destombes K S, Van der Heijden M C, Van Harten A. Availability of k-out-of-n systems under block replacement sharing limited spares and repair capacity [J]. International Journal of Production Economics, 2007, 107(2): 404-421.
[4]卢雷, 杨江平, 左治方, 等. 大型相控阵雷达天线阵面视情维修优化模型 [J]. 雷达科学与技术, 2014, 12(3): 325-328.
LU Lei, YANG Jiangping,ZUO Zhifang,et al. Optimal analysis of condition-based maintenance model or large-scale phased array radar antenna [J]. Radar Science and Technology, 2014, 12(3): 325-328. (in Chinese)
[5]卢雷, 杨江平. 任意寿命分布下k/n(G)系统定时维修决策模型 [J]. 现代防御技术, 2015, 43(1): 145-149.
LU Lei, YANG Jiangping. Time based maintenance optimization model for k/n (G) system with various lifetime distribution [J]. Modern Defence Technology, 2015, 43(1): 145-149. (in Chinese)
[6]张光义, 赵玉洁. 相控阵雷达技术 [M]. 北京: 电子工业出版社, 2006.
ZHANG Guangyi, ZHAO Yujie. Phased array radar technology [M]. Beijing: Electronic Industry Press, 2006. (in Chinese)
[7]张良. 低副瓣固态有源相控阵天线可靠性分析 [J]. 现代雷达, 1992(6): 97-105.
ZHANG Liang. Analysis on the reliability of low-sidelobe solid-state active phased array antenna [J]. Modern Radar, 1992(6): 97-105. (in Chinese)
[8]李建新, 高铁. 低副瓣固态有源相控阵天线波瓣统计特性研究 [J]. 电波科学学报, 1993, 8(2): 64-69.
LI Jianxin, GAO Tie. Statistical pattern characteristics of low sidelobe solid-state active phased array antennas [J]. Chinese Journal of Radio Science, 1993, 8(2): 64-69. (in Chinese)
[9]高铁, 李建新. 固态有源相控阵天线多阶振幅量化及副瓣特性的研究 [J]. 电子学报, 1994, 22(3): 11-17. GAO Tie, LI Jianxin. Study of multi-step quantization and sidelobe characteristic for solid-state active phased arrays[J]. Acta Electronica Sinica, 1994, 22(3): 11-17. (in Chinese)
[10]Visser H J. Array and phased array antenna basics [M]. Netherlands: John Wiley & Sons Inc., 2005.
[11]傅文斌. 微波技术与天线 [M]. 北京: 机械工业出版社, 2007.
FU Wenbin.Microwave technique and antenna [M]. Beijing: China Machine Press, 2007. (in Chinese)
[12]郭燕昌, 钱继曾, 黄富雄, 等. 相控阵和频率扫描天线原理 [M]. 北京: 国防工业出版社, 1978.
GUO Yanchang, QIAN Jizeng, HUANG Fuxiong, et al. Phased array and frequency scanning antenna [M]. Beijing: National Defence Industry Press, 1978. (in Chinese)
[13]徐福荣. 由成败型元件组成的k/n(G)系统的可靠性评定与综合 [J]. 兵工学报, 1990(1): 66-74.
XU Furong. Confidence limits of reliability for the “k-of-n” systems consisting of different binomial components [J]. Acta Armamentarii, 1990(1): 66-74. (in Chinese)
[14]梅启智, 廖炯生, 孙惠中. 系统可靠性工程基础 [M]. 北京: 科学出版社, 1992.
MEI Qizhi, LIAO Jiongsheng, SUN Huizhong. System reliability engineering foundation [M]. Beijing: Science Press, 1992. (in Chinese)
[15]徐维新, 刘梦军, 何杰, 等. 维修工程学 [M]. 北京: 电子工业出版社, 1992.
XU Weixin, LIU Mengjun, HE Jie, et al. Maintenance engineering [M]. Beijing: Electronic Industry Press, 1992. (in Chinese)
[16]甘茂治, 康建设, 高崎. 军用装备维修工程学[M]. 北京: 国防工业出版社, 2009.
GAN Maozhi, KANG Jianshe, GAO Qi. Military equipment maintenance engineering [M]. Beijing: National Defence Industry Press, 2009. (in Chinese)
doi:10.11887/j.cn.201602016
*收稿日期:2015-03-17
基金项目:国家自然科学基金资助项目(61401503);国家部委基金资助项目(KJ2014023200B11145);博士研究生专项资助项目(2014JY546)
作者简介:王永攀(1987—),男,河北保定人,博士研究生,E-mail: wypaning@163.com;杨江平(通信作者),男,教授,博士,博士生导师,E-mail: yjp_wh@163.com
中图分类号:TN95
文献标志码:A
文章编号:1001-2486(2016)02-092-07
Maintenance optimal model for phased array antenna with regional quantification
WANG Yongpan1, YANG Jiangping1, ZHANG Yu2, LI Lujun1,3
(1. Land-based Early Warning Equipment Department, Air Force Early Warning Academy, Wuhan 430019, China;2. College of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan 430068, China;3. The PLA Unit 93975, Wulumuqi 830000, China)
Abstract:There exist several problems in the maintenance of phased array antenna, such as high maintenance costs, unsure maintenance chance, complicated model simulation and arithmetical operation. Considering these problems, a maintenance optimal model was put forth on the basis of regional quantification. A regional quantification model was given, and then the maintenance problems of phased array antenna were turned into the maintenance optimal of a k/n system, which consists of different regional array elements. A maintenance optimal model for the antenna was built, which chooses minimum maintenance costs per unit time as the object and the operational availability as the subject. Simulations and analysis of one instance were conducted to verify the validity of the proposed model. The results show that the proposed model could solve the maintenance problems of the asymmetrical array antenna well.
Key words:regional quantification; maintenance optimal model; phased array antenna; array element; linear array
http://journal.nudt.edu.cn

