GNSS自适应天线相位中心评估方法*

李立勋，庞　晶，陈华明，王飞雪

(国防科技大学 电子科学与工程学院， 湖南 长沙　410073)



GNSS自适应天线相位中心评估方法*

李立勋，庞晶，陈华明，王飞雪

(国防科技大学 电子科学与工程学院， 湖南 长沙410073)

摘要：自适应天线在波束形成过程中会引起天线相位中心变化，针对这一问题，提出一种基于可用波束的自适应天线相位中心评估方法。该方法分为三步：设置天线的可用波束门限；在干扰来向均匀分布下，得到天线可用波束门限内相位方向图集合；利用最小二乘法对相位方向图集合进行拟合得到自适应天线的平均相位中心变化量。运用该方法对四种典型的四元阵相位中心进行对比仿真，结果表明，算法可以快速有效地对自适应天线相位中心性能进行评估。另外，通过设置适当的可用波束门限，可以提高自适应天线的相位中心性能。算法的评估结果可以作为GNSS高精度自适应天线阵型选择依据。

关键词：全球卫星导航系统；自适应天线；可用波束率；平均相位中心偏移量；平均相位中心变化量

全球卫星导航系统(Global Navigation Satellite System, GNSS)能够为用户提供高精度的定位、导航和授时服务，在军民领域都有广泛的应用。但是由于卫星发射信号功率有限，到达地面的信号非常微弱，容易受到各种有意或是无意射频干扰的影响，导致接收机精度变差甚至无法工作[1]。

自适应天线是GNSS中消除射频干扰的有效手段，通过调节天线阵合成方向图在干扰方向形成零陷，在期望信号方向形成主瓣，从而实现对干扰的抑制[2-4]。但是自适应天线阵在进行干扰抑制的同时，也对有用信号产生了影响，主要体现在：①在干扰方向产生零陷，导致天线可用波束减少；②波束形成过程中，对阵元加权引起天线阵合成方向图相位特性发生变化[5-7]。

在民用接收机中，天线相位中心波动引入的测量误差通常可以忽略。对于高精度GNSS应用，测量误差要求对于伪距测量而言一般在厘米(cm)级，对于载波相位测量而言一般为毫米(mm)级。而天线相位中心变化引入的测量误差通常达到了厘米(cm)级。因此天线相位中心是影响测量精度的主要因素，需要评估天线的相位中心性能[8-9]。

对于固定波束天线，天线相位中心在每个俯仰角是固定的，可以通过在暗室标定出天线在对应俯仰角的相位中心特性来实现对天线相位中心的评估[10]。对于自适应天线，波束根据干扰的不同而变化，相位方向图不固定，传统的固定波束相位中心评估方法已经不可用[11]。

对于自适应天线阵的研究，目前主要集中在天线可用率与服务性能上[12-13]，对于相位中心的研究还很少。文献[14-15]通过推导阵列天线相位方向图与相位中心偏移量的关系，提出了一种阵列天线相位中心测量方法，但是均是基于波束形成后单一波束相位中心测量实现的，本质上与固定波束天线测量方法相同。

1自适应天线阵方向图

1.1阵型模型

天线阵列由N个阵元组成，取坐标原点为参考点，一路信号源从(θ,φ)的入射角到达天线口面，阵列结构如图1所示[16]。

其中Pi(xi,yi,zi)(i=1,2,…,N) 表示第i个天线阵元的坐标位置，(θ,φ)为信号来波方向，天线阵列对于(θ,φ)方向来波信号的方向矢量为：

a(θ,φ)=[e-jτ1(θ,φ),e-jτ2(θ,φ),…,e-jτN(θ,φ)]T

(1)

式中，τi(θ,φ)=2πPi·r/λ表示第i个阵元接收到的信号与到达阵列中心的波前的相位差，T表示矩阵转置，r=[sinθcosφ, sinθsinφ, cosθ]T表示来波信号方向的单位矢量，λ表示信号中心频点波长。

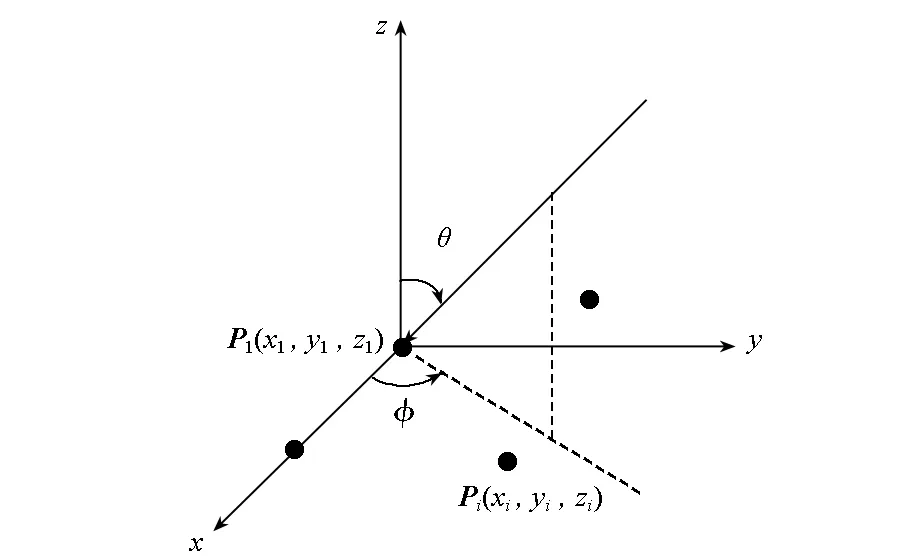
图1　天线阵结构示意图Fig.1　Antenna array configuration

1.2天线阵幅度与相位方向图

在自适应天线阵中，应用不同的抗干扰准则，阵列权值通常不同，一般可由式(2)得到[17]：

(2)

式中，w=[w1,wi,…,wN],s是算法导向矢量，其值取决于不同的抗干扰算法，H表示矩阵共轭转置，R是输入信号相关矩阵。

则阵列辐射方向图为：

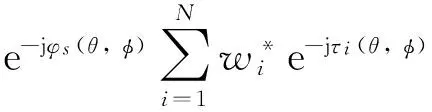
(3)

式中，Ps(θ,φ)，φs(θ,φ)分别是天线阵元的幅度方向图和相位方向图。

波束形成后的归一化幅度方向图以dB为单位可以表示为：

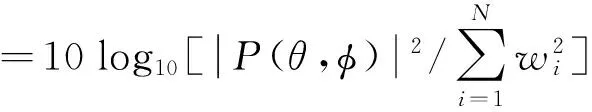
(4)

相位方向图可以表示为：

ψ(θ,φ)=∠P(θ,φ)

(5)

2可用波束平均相位中心

2.1天线相位中心

电气电子工程师协会(Institute of Electrical and Electronics Engineers, IEEE)对天线相位中心的定义[18]为：

一个半径足够达到远场要求的球体，在这个球体的表面或是至少辐射强度比较大的部分的表面，给定场量的相位是不变的，这个球体的中心所在位置即是天线的相位中心。

在GNSS应用中，确定天线相位中心的三个指标为平均参考点位置ARP、相位中心偏移量PCO和相位中心变化量PCV，如图2所示。其中PCV是影响接收机测量精度的主要因素[19]。

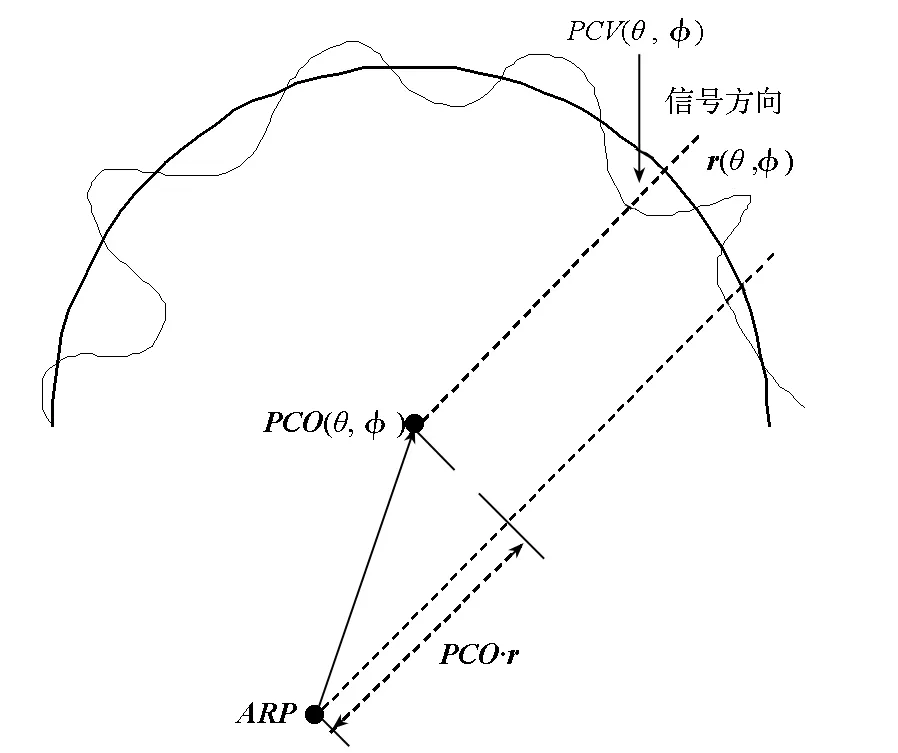
图2　天线相位中心模型Fig.2　Phase center model of antenna

天线的远场相位方向图可以表示为：

ψ(θ,φ)=ψ0+k(xcosφsinθ+ysinφsinθ+zcosθ)

(6)

式中，(x,y,z)是天线的PCO坐标，ψ0是固定相位偏差，k为波常数。

传统的相位中心评估中[20-21]，当得到天线的相位方向图ψ(θ,φ)后，通过拟合式(6)，得到天线在不同俯仰角的PCO和PCV值。PCO和PCV均是俯仰角函数。

2.2可用波束定义

自适应天线波束随干扰来向实时变化，天线相位方向图也实时变化，传统固定波束相位中心评估方法已经不可用。为了评估自适应天线的相位中心，首先定义可用波束率：

自适应天线波束形成后，波束范围内最大增益为Gmax。任取天线前向中的方位点，如果该方位点对应的增益不小于Gmax-GT，则称该方位点为GT可用方位点。所有GT可用方位点的集合定义为GT可用波束，GT为可用波束门限。GT可用波束与整个天线前向波束之比定义为GT可用波束率。

可用波束门限GT时可用波束率ABR表示为：

(7)

式中，S(0°≤θ≤90°,0°≤φ<360°)表示天线前向所有区域面积，S(G(θ,φ)≥Gmax-GT)表示GT可用波束面积。

2.3平均相位中心变化量计算

干扰来波方向服从随机均匀分布，得到不同干扰方向下GT可用波束宽度的波束相位方向图集合如式(8)所示：

ψ(GT)={ψ1(GT),ψ2(GT),…,ψK(GT)}

(8)

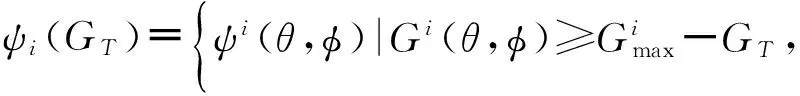
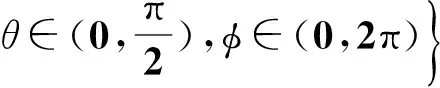
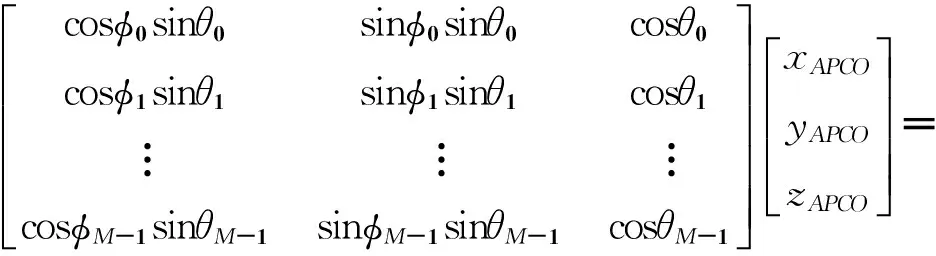
(9)

式中，(θi,φj)={(θ,φ)|ψ(θ,φ)⊆ψ(GT)},M表示(θ，φ)的维数，取决于(θ，φ)计算步径。xAPCO，yAPCO，zAPCO分别表示平均相位中心偏移量APCO的坐标值。

运用最小二乘法对式(9)进行拟合，得到可用波束内APCO如式(10)所示。

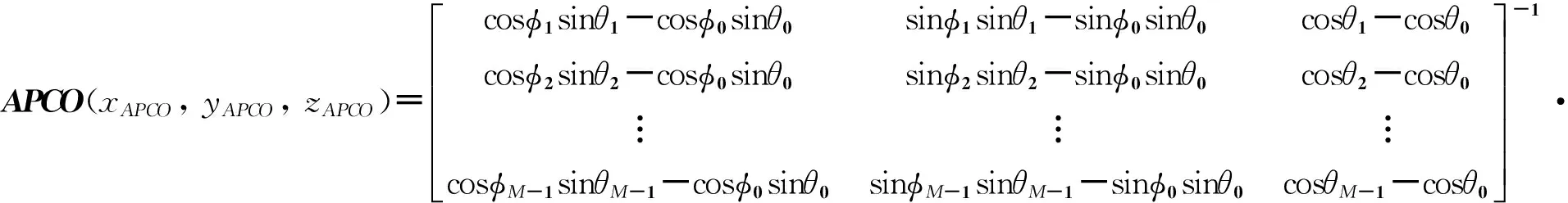
(10)

求拟合残差得到平均相位中心变化量APCV为：

(11)

3仿真与分析

基于以上自适应天线相位中心评估方法，本节对四种常见GNSS自适应天线阵型进行了评估。阵元为圆极化微带贴片天线。

3.1阵元设计及性能评估

微带天线是GNSS自适应天线阵主要阵元类型。在本设计中，阵元为双馈右旋圆极化贴片天线,通过使用双馈电点技术实现了圆极化。单天线的可用波束率及相位中心变化量如图3所示。

可见，对于单天线而言，可用波束率随可用波束门限增加而增加，当门限设置在8 dB以上时，可用波束率达到100%；相位中心变化量随着可用波束门限增加而变大，可用波束门限达到8 dB以上时，其达到最大0.7 mm。

图3　微带天线阵元特性Fig.3　Characterization of microstrip antenna elements

3.2阵型设计

天线阵元分布在一个半径为中心频点波长的圆形平面口径上，包含4个微带贴片阵元，四种不同的阵元分布方式如图4所示：均匀中心圆阵(A1)；非均匀中心圆阵(A2)；均匀圆阵(A3)；非均匀圆阵(A4)。

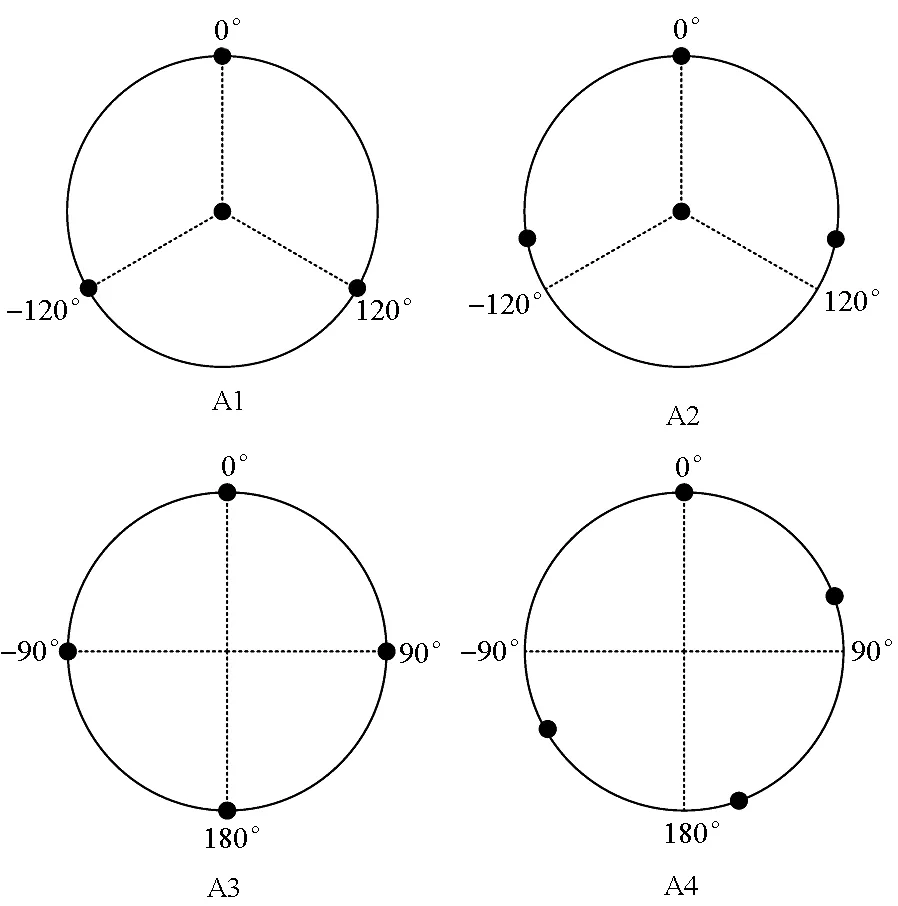
图4　不同的阵元分布Fig.4　Various distributions of antenna elements

3.3仿真结果

设定所有干扰信号是互不相关的窄带信号，干信噪比为20 dB，抗干扰算法采用功率倒置算法[16,22]。对于同一阵型，干扰信号入射方向在天线阵平面上服从均匀分布，对每种阵型干扰场景数设置为200。

图5为存在0到3路干扰时，四种阵型的可用波束率随可用波束门限变化情况。在干扰存在时，随着可用波束门限增加，可用波束率逐渐增加。对于同一阵型，干扰存在时的可用波束率高于无干扰时可用波束率，这是由干扰存在时天线可用波束内增益变化趋于平缓导致的。随着干扰数量的增加，可用波束率逐渐降低。比较四种阵型，A1可用波束率最高，A2次之，A3可用波束率最低，总体而言，四种阵型的可用波束率相近。

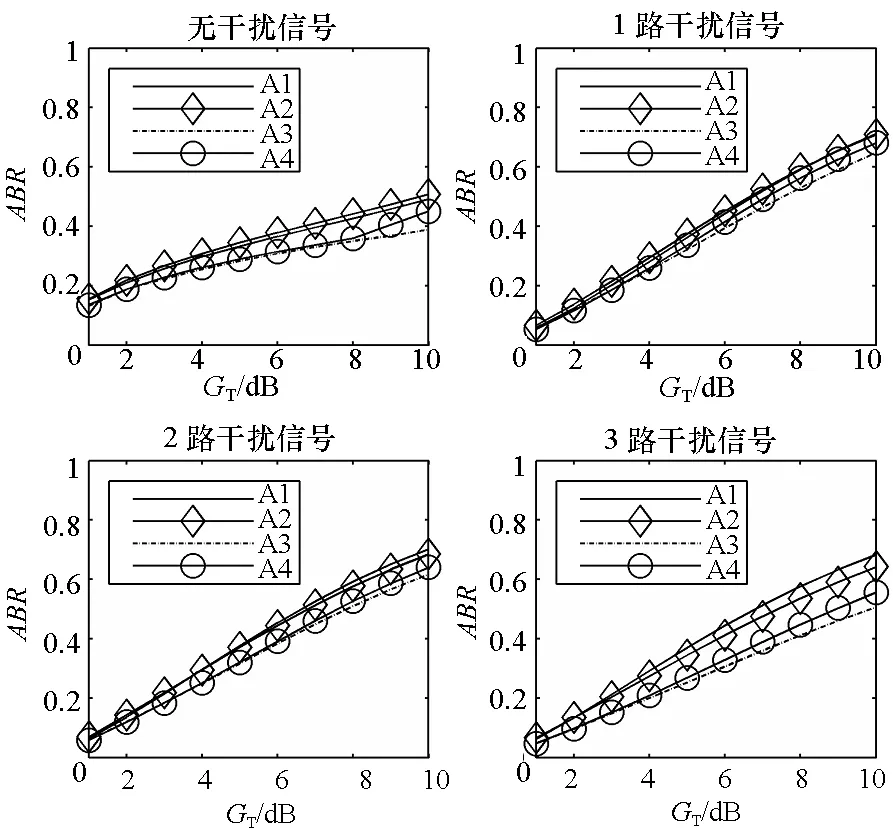
图5　可用波束率随波束门限变化情况Fig.5　The ABR versus the GT

图6为0到3路干扰存在时，四种阵型的平均相位中心变化量随可用波束门限变化情况。无干扰时，A3阵型的相位中心变化量最佳，接近0 mm；A1与A2相近；当可用波束门限达到7 dB以上时，A4平均相位中心变化量迅速增大，达到10 mm以上。干扰存在时，四种阵型的平均相位中心变化量比无干扰时明显增大，但随着干扰数量增加变化不大。比较四种阵型的平均相位中心变化量，无干扰时，A3最佳；干扰存在时，A2阵型最佳，A4次之，A3最差。

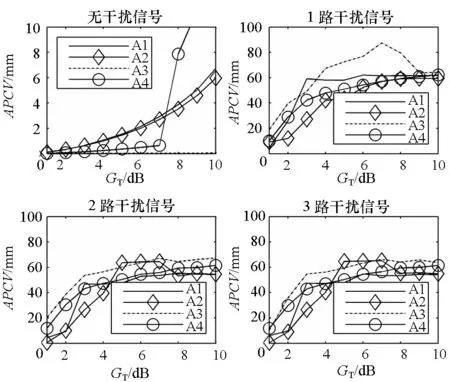
图6　平均相位中心变化量随波束门限变化情况Fig.6　Output APCV versus the GT

综上，无论有无干扰存在，四种阵型的可用波束率都相近。无干扰时，A3阵型由于结构对称，平均相位中心变化量最低。但是当干扰存在时，由于自适应天线波束不对称，天线阵型对称作用消失，A2阵型达到最佳。

4结论

提出基于可用波束率的GNSS 自适应天线相位中心评估方法，基于该方法对4种典型的自适应天线阵相位中心性能进行了评估。算法可以快速有效地对自适应天线阵相位中心特性进行评估。

在高精度GNSS 应用中，对于自适应天线，在干扰方向随机分布情况下，A2 是最佳的高精度自适应天线阵型选择。根据该算法评估结果设置适当的可用波束门限可以实现不同的测量精度要求，同时该算法也可以作为高精度自适应天线阵型的选择依据。

参考文献(References)

[1]Fante R L, Vaccaro J J. Wideband cancellation of interference in a GPS receive array[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(4): 549-564.[2]Motella B, Savasta S, Margaria D, et al. Method for assessing the interference impact on GNSS receivers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1416-1432.

[3]Arribas J, Fernandez-Prades C, Closas P. Antenna array based GNSS signal acquisition for interference mitigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 223-243.

[4]Li Q, Wang W, Xu D J, et al. A robust anti-jamming navigation receiver with antenna array and GPS/SINS[J]. IEEE Communications Letters, 2014, 18(3): 467-470.

[5]O′Brien A J, Gupta I J. Mitigation of adaptive antenna induced bias errors in GNSS receivers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 524-538.[6]Vagle N, Broumandan A, Jafarnia A, et al. Characterization of GNSS measurement distortions due to antenna array processing in the presence of interference signals[C]//Proceedings of Ubiquitous Positioning Indoor Navigation and Location Based Service, IEEE, 2014: 71-80.

[7]Zhang Y D, Amin M G. Anti-jamming GPS receiver with reduced phase distortions[J]. IEEE Signal Processing Letters, 2012, 19(10): 635-638.

[8]Yu S, Zhan Y, Pei Y. The effect of group-delay difference for wideband antenna arraying: degradation and its solution[C]// Proceedings of 4th IEEE International Conference on Information Science and Technology, IEEE, 2014: 498-501.[9]Miller P. The measurement of antenna group delay[C]// Proceedings of 8th European Conference on Antennas and Propagation, IEEE, 2014: 1488-1492.

[10]Sharawi M S, Aloi D N. Null steering approach with minimized PCV and GD for large aperture vertical antenna arrays [J]. IEEE Transactions on Antennas and Propagation, 2007, 55(7): 2120-2213.

[11]De Lorenzo D S, Lo S C, Enge P K, et al. Calibrating adaptive antenna array for high-integrity GPS [J]. GPS Solut, 2012, 16(2): 221-230.

[12]王瑛, 刘小汇, 王飞雪. 基于可用率的自适应阵抗干扰性能评估[C]//2007全国天线年会, 2007: 114-117.

WANG Ying, LIU Xiaohui, WANG Feixue. Availability ratio based evaluation of anti-jamming performance of adaptive arrays[C]//Proceedings of NCAnt2007, 2007: 114-117. (in Chinese)

[13]聂俊伟, 葛锐, 李垣陵, 等. 基于导航定位服务性能的GNSS天线阵抗干扰统计性能评估方法[J]. 国防科技大学学报, 2012, 34(2): 81-87.

NIE Junwei, GE Rui, LI Yuanling,et al. Performance evaluation method for GNSS anti-jam antenna arrays based on the navigation service performance[J]. Journal of National University of Defense Technology, 2012, 34(2): 81-87. (in Chinese)

[14]陈曦, 傅光, 龚书喜, 等. 阵列天线相位中心的校准方法及误差分析[J]. 西安电子科技大学学报(自然科学版), 2011, 38(3): 145-149.

CHEN Xi, FU Guang, GONG Shuxi, et al. Study on calibration of phase center of array antenna and its error analysis[J].Journal of Xidian University(Natural Science), 2011, 38(3): 145-149. (in Chinese)

[15]陈曦, 傅光, 龚书喜, 等. 阵列天线相位中心的测量方法研究[J]. 微波学报, 2011, 27(1): 36-39.

CHEN Xi, FU Guang, GONG Shuxi, et al. Study on measurement of phase center of array antenna[J]. Journal of Microwaves, 2011, 27(1): 36-39. (in Chinese)

[16]Meng D W, Feng Z M, Lu M Q. Anti-jamming with adaptive arrays utilizing power inversion algorithm[J]. Tsinghua Science & Technology, 2008, 13(6): 796-799.

[17]孙莉. 卫星导航简化分布式矢量天线抗干扰和多径抑制技术研究[D]. 长沙: 国防科学技术大学, 2011.

SUN Li. Research on anti-jamming and multipath mitigation by reduced distributed vector sensor in satellite navigation systems [D]. Changsha: National University of Defense Technology, 2011. (in Chinese)

[18]IEEE standard definition of terms for antenna[S]. IEEE standard No. 145-1993, ISBN 1-5593-7317-2, 1973.

[19]Kunysz W. Antenna phase center effects and measurement in GNSS ranging applications[C]// Proceedings of 14th International Symposium on Antenna Technology and Applied Electromagnetics & the American Electromagnetics Conference (ANTEM and AMEREM), 2010: 1-4.

[20]尚军平, 傅德民, 邓颖波. 天线相位中心的精确测量方法研究[J]. 西安电子科技大学学报(自然科学版), 2008, 35(4): 673-677.SHANG Junping, FU Demin, DENG Yingbo. Research on the accurate measurement method for the antenna phase center[J].Journal of Xidian University(Natural Science), 2008, 35(4): 673-677. (in Chinese)

[21]Kumar A, Sarma A D, Ansari E, et al. Improved phase center estimation for GNSS patch antenna[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(4):1909-1915.

[22]吴仁彪, 孙擎宇, 胡铁乔, 等. 基于功率倒置算法的GPS 抗干扰实时系统实现[J]. 中国民航大学学报, 2010, 28(3): 45-48.

WU Renbiao, SUN Qingyu, HU Tieqiao, et al. Realization of GPS anti-jamming real-time system based on power inversion algorithm[J]. Journal of Civil Aviation University of China, 2010, 28(3): 45-48. (in Chinese)

doi:10.11887/j.cn.201602015

*收稿日期：2015-03-07

基金项目：中国第二代卫星导航系统重大专项资助项目(GFZX0301020210)

作者简介：李立勋(1985—)，男，山西长治人，博士研究生，E-mail：lilixun1985@163.com；王飞雪(通信作者)，男，教授，博士，博士生导师，E-mail：wangfeixue_nnc@163.com

中图分类号：TN911.72

文献标志码：A

文章编号：1001-2486(2016)02-087-05

Phase center evaluation method in adaptive GNSS antenna

LI Lixun, PANG Jing, CHEN Huaming, WANG Feixue

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：Beam forming processing of adaptive antenna introduces the change of antenna phase center. In order to solve this problem, an evaluation method of adaptive antenna phase center on the basis of available beam was proposed. The method achieved the purpose in three steps: setting the available beam threshold; obtaining phase pattern set in available beam areas when the direction of interference signal distributed uniformly; fitting the phase pattern set to get the average phase center variations of adaptive antenna by using least square method. The method was validated by simulation under four typical four-elements-arrays. The analysis of simulated results indicates that the proposed method can be used to evaluate the phase center characters of adaptive antenna conveniently. What’s more, in order to fulfill the performance of high precision for adaptive antenna array, a choice is to reduce the available beam threshold. The research can be used as a guideline for choice of distributions of antenna elements in high-precision GNSS.

Key words：global navigation satellite system; adaptive antenna; available beam ratio; average phase center offset; average phase center variation

http://journal.nudt.edu.cn