利用局部评估的分布式图模式匹配算法*
张丽霞,王伟平,高建良,王建新
(1.中南大学 信息科学与工程学院, 湖南 长沙 410083; 2.湖南师范大学 数学与计算机学院, 湖南 长沙 410081)
利用局部评估的分布式图模式匹配算法*
张丽霞1,2,王伟平1,高建良1,王建新1
(1.中南大学 信息科学与工程学院, 湖南 长沙410083; 2.湖南师范大学 数学与计算机学院, 湖南 长沙410081)
摘要:为了在分布式存储的大规模数据图上进行快速图模式匹配,提出利用局部评估的分布式图模式匹配算法。各计算节点并行地执行本地匹配;协调器节点收集局部匹配结果、计算边界点的匹配状态并发送给相应的计算节点;计算节点根据边界点的匹配状态确定与边界点相连的节点的匹配情况;协调器节点组合得出最大匹配集。实验结果表明:与已有的分布式图模式匹配算法相比,disGPM-PE算法都能够在不显著增加通信量的前提下避免数据片段间的依赖关系对执行时间的影响,从而减少图模式匹配的时间。
关键词:图模式匹配;分布式算法;局部评估
来自互联网及生活中的海量数据之间存在紧密的关联性,图作为一种被广泛应用的数据结构,非常适合刻画这种具有关联性的数据,图中的每个顶点代表现实世界中的实体对象,顶点之间的边表示实体之间的关系。图模式匹配是从一个数据图中找出与给定查询图(模式图)相同或相似的子图。图模式匹配通常定义为子图同构[1]。由于子图同构是NP完全问题(Non-determinsitic Polynomial Complete problem, NPC)并且在有些实际应用中发现有意义的匹配时过于严格,因此现实生活中图模式匹配通常定义为图模拟[2]。图模拟把图模式匹配定义为模式图中节点和数据图中节点之间的对应关系,要求数据图中节点保持模式图中对应节点的后继关系。图模式匹配应用十分广泛,例如在社交网络中用于社团发现,在万维网中用于Web文档分类,在软件工程领域用于软件代码剽窃检测[3]以及在生物领域用于蛋白质结构检测和功能预测等。
随着社交网络、生物网络和Web网络等的快速发展,互联网数据量急剧增长。已有的图模式匹配算法面临新的挑战:一方面,大规模的数据无法集中存储在一个数据中心上,只能分布存储在多个数据中心上,而且数据中心的地理位置通常较远;另一方面,数据规模的显著增大导致用于表示数据及数据间关系的图的规模显著增大,即使采用分布式算法进行图模式匹配也会面临通信量大、延迟长的问题,如何面向大规模图提高分布式算法的并行效率成为关键。文献[4]提出的分布式图模式匹配算法把存储在不同计算节点上的连通子图发送到一个计算节点上进行图模式匹配,缺点是计算节点间通信量较大。文献[5]提出的分布式算法只在计算节点间传送边界点的匹配状态,但需要每个计算节点建立本地的逻辑依赖图,对于存在多个节点上的连通子图,各节点需要依次等待消息才能进行下一轮的匹配,执行时间与计算节点上数据片段间的依赖关系相关。文献[6]提出了以顶点为中心的分布式图模式匹配方法,当图中节点个数多时,效率不高。另外,消息传递机制使得可以并行的操作序列化,从而降低了并发性。
为了在减少网络通信量的同时避免数据片段间的依赖关系对执行时间的影响,本文借鉴文献[7]针对分布式图上的节点间可达性查询问题的解决方法,通过对其思想进行改进和优化,提出了基于局部评估的分布式图模式匹配算法(distributed Graph Pattern Matching based on Partial Evaluation, disGPM-PE)。算法的基本过程如下:首先各计算节点并行地执行本地匹配,然后协调器节点收集局部匹配结果、计算边界点的匹配状态并发送给相应的计算节点,接着计算节点根据边界点的匹配状态确定与边界点相连的节点的匹配情况,最后协调器节点组合得出最大匹配集。与先前的算法相比,disGPM-PE算法具有如下特点:①各计算节点并行进行本地匹配,能够避免某些分布式算法将分布在不同计算节点上的连通子图发送到一个计算节点上集中处理,造成较大通信量的问题;②所有计算节点进行局部评估时完全并行,收到协调器节点的求值结果后继续确定与边界点相连的节点的匹配状态时仍然是完全并发执行的;③协调器节点收集来自所有计算节点的匹配结果、边界点相关的布尔表达式,求值后将结果发给各计算节点。虽然在计算节点和协调器节点之间额外传送布尔表达式和求值结果在一定程度上增加了通信量,但是各计算节点的匹配次数固定为两次,匹配次数和并发度不受计算节点上的数据片段之间的依赖关系的限制。
1图模式匹配相关定义
对于图模式匹配,模式图和数据图都是带标签的有向图,图中的每个节点有且仅有一个标签,该标签定义了节点的属性(如:关键词、技能、等级、姓名、公司等),相关定义如下:
定义1(图)G=(V,E,L)是一个图,V是节点集,EVV是边集,L是一个标签函数,V中的每个节点都有一个标签att,即L(v)=att,att是v的属性。
定义2(图模式匹配)假设有一个模式图P=(Vp,Ep,Lp)和一个数据图G=(V,E,L),u和v分别是P和G中的节点。如果存在一个二元关系RVpV,满足:
1)如果(u,v)∈R,那么u和v有相同的标签即Lp(u)=L(v);
2)对Vp中的任意一个节点u,V中都存在一个节点v,使得:(u,v)∈R;对Ep中的任意一条边(u,u′),在E中都存在一条边(v,v′)使得(u′,v′)∈R;
则说G匹配P,标识为P◁G,R是一个匹配。对于任意P和G,如果G匹配P,一定存在一个最大的匹配关系。图模式匹配问题就是:如果P◁G,那么在G中为P找出一个最大匹配R。
定义3(分布式图)G=(V,E,L)一个分布式图,F={F1,F2,…,Fk}称作G的一个划分,其中每个片段Fi={Vi∪Fi.O,Ei∪CEi,Li∪Li.O}(1≤i≤k)且以下条件成立:
1)V={V1∪V2∪…∪Vk};
2)任一(Vi,Ei,Li)是G的一个子图;
3)对Vi中的任一节点u,如果E中存在一条边(u,v)且v在另一个片段中,那么v称作是Fi的一个虚节点(virtual node),Fi.O是Fi的虚节点的集合。相应地,如果存在一条从片段Fj中的节点v到片段Fi中的节点u的跨边(v,u),那么u称作是Fi的一个入节点(in node),我们用Fi.I表示Fi的入节点集合;
4)CEi={(u,v)|(u,v)∈E,u∈Vi,V∈Fi.O}是从Vi到其他片段中节点跨边的集合。
2disGPM-PE算法
2.1算法主要思想及流程
在disGPM-PE算法中,每个计算节点处理的节点被分为以下几类:虚节点、内部节点、与虚节点相连的节点和入节点。虚节点是存储在别的数据片段和计算节点上、被复制一份存在本地的节点,本地仅知道其标签而不知其孩子节点,算法在进行本地处理时只能根据其标签把它加入对应节点的匹配集中而不能根据后继点对其进行筛选确定其最终匹配状态,这种匹配可能不是真的匹配、不会出现在最终的匹配集中,属于局部匹配;内部节点是指和虚节点没有关系的节点,算法仅根据本地数据就可以确定这些节点的匹配状态;与虚节点相连的节点是指有路径到达虚节点的节点,如果本地不能确定其匹配状态,就把它们加入局部匹配集中;入节点是指存在一条来自于其他数据片段上边的节点,如果其匹配状态与虚节点匹配状态有关,则可用一个布尔表达式描述它们之间的关系。
假设数据图G的一个划分F={F1,F2,…,Fk},每一个片段Fi存放在一个计算节点Mi上,模式图及图模式匹配请求发送给一个协调器节点Mc。disGPM-PE算法流程如图1所示。
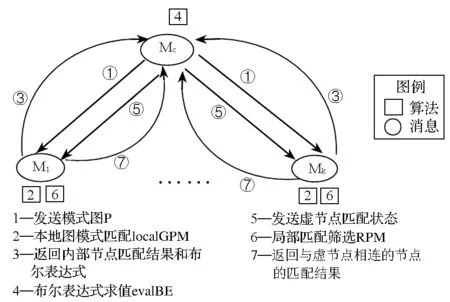
图1 disGPM-PE算法流程图Fig.1 Algorithm flow chart of disGPM-PE
算法具体操作过程如下:①协调器节点Mc把模式图发给每个计算节点;②每个计算节点收到模式图P后,并行地调用本地图模式匹配子算法(local Graph Pattern Matching,localGPM),根据本地数据执行图模式匹配,产生三个集合:内部节点匹配结果Mi.C,与虚节点相连的节点的匹配结果Mi.U和布尔表达式集合Mi.beset;③每个计算节点把第二步产生的Mi.C和Mi.beset发送给协调器节点Mc;④Mc把从每个计算节点收集的Mi.beset组合成一个布尔表达式系统,调用布尔表达式求值子算法(evaluate Boolean Expressions,evalBE)求得各虚节点的匹配状态;⑤Mc把虚节点的匹配状态发给各计算节点;⑥各计算节点执行局部匹配筛选子算法(Refining Partial Matching,RPM)对局部匹配集Mi.U进行筛选,确定与虚节点相连的节点的匹配状态,匹配结果存入最终匹配集Mi.F中;⑦各计算节点把与虚节点相连的节点的匹配结果发到Mc。最终,协调器节点Mc把从各计算节点收到的所有匹配结果组合在一起,就得到了最大匹配集M。
2.2本地图模式匹配子算法localGPM
当每个计算节点Mi收到模式图P后,并行地调用localGPM根据本地数据Fi执行图模式匹配,输出三个集合:内部节点的匹配集Mi.C、局部匹配集Mi.U和布尔表达式集Mi.beset。其执行过程如下:首先,仅根据标签产生模式图中的各个节点的候选匹配集;然后,对候选匹配集中的内部节点根据后继进行筛选,产生内部节点的匹配集Mi.C;接着,对候选匹配集的虚节点w,假设它属于模式图中节点u的候选匹配集且u在模式图中有后继,则将w加入局部匹配集Mi.U中并在Mi.beset中加入一个布尔变量X(u,w),表示需要从协调器节点获知w是否匹配u,对于候选匹配集中与w相连的节点w′,如果其匹配状态取决于w的匹配状态,则将其加入局部匹配集Mi.U;最后,对局部匹配集中Fi中的入节点v,求出一个布尔表达式加入Mi.beset,该表达式表示v匹配u需要Fi中的虚节点满足的条件。
图2给出一个分布式数据图和需要查找的模式图的实例,图2(a)为模式图,图2(b)为数据图。
设F1~F4分别存放在计算节点M1~M4上。在M1上除A2为入节点且与虚节点相连外,A1~H1均为内部节点,在执行localGPM时,所有内部节点都是和模式图中的点匹配的,因此M1.C包括所有的内部节点;B2和C2是虚节点,将它们加入局部匹配集Mi.U,并把X(B,B2)和X(C,C2)加入M1.beset,A2与虚节点B2及C2相连且其匹配状态不确定的,因此A2也加入Mi.U;由于A2是入节点,因此将布尔表达式X(A,A2)=X(B,B2)∧X(C,C2)加入M1.beset。各计算节点执行localGPM算法后的结果如表1所示。

表1 各计算节点执行localGPM后的结果
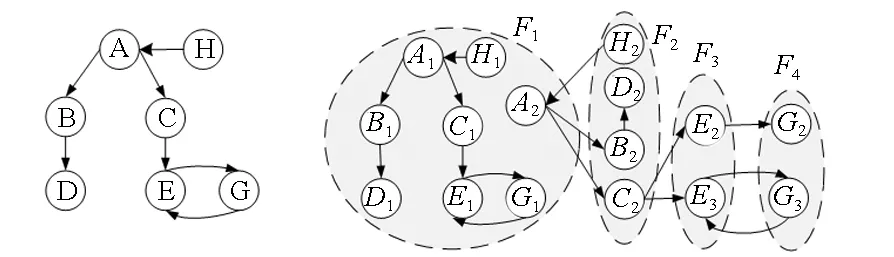
(a)模式图(a) Pattern graph (b)数据图(b) Data graph图2 分布式数据图和模式图的一个实例Fig.2 An example of distributed data and pattern graph
2.3布尔表达式求值子算法evalBE
当各计算节点把本地匹配的结果Mi.C和Mi.beset发送给协调器节点Mc后,Mc先组合这些结果得到M和布尔表达式集合(BEset),然后执行布尔表达式求值子算法evalBE得到所有布尔表达式的值。
子算法evalBE首先根据BEset建立虚节点匹配状态逻辑关系图,然后对逻辑关系图中的各节点求值。建立虚节点匹配状态逻辑关系图的过程如下:Beset中的每个布尔变量对应逻辑关系图中的一个节点;由于一个布尔等式左边的布尔变量的值和右边的布尔变量的值有关系,因此对于每个布尔等式,代表等式左边的布尔变量的节点和每个代表等式右边的变量的节点之间存在一条边,连接等式右边的变量之间的逻辑运算符作为代表等式左边布尔变量的节点的属性,当等式右边只有一个布尔变量时,代表等式左边布尔变量的节点的属性为空。
对于图2中的实例,建立的虚节点匹配状态逻辑关系图如图3所示。根据该逻辑关系图对图中各节点求值的过程如下:首先,由于叶节点(G,G2)不属于M,因此X(G,G2)为假;其次,因为节点X(E,E3)和节点X(G,G3)形成一个环,互为依赖条件,所以它们的值都为真;最后,按照广度优先搜索的逆序依次对逻辑关系图的剩余节点求值,能够得到逻辑关系图中所有节点的值。求值过程结束后,协调器节点把得到的布尔表达式的值发送给需要这些值的计算节点。
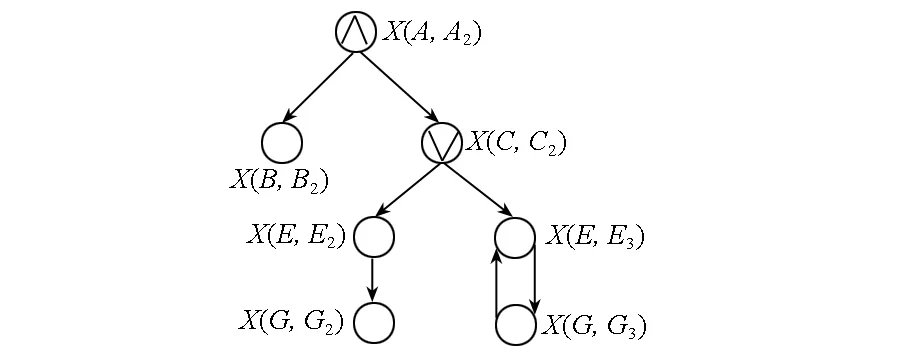
图3 根据BEset建立的虚节点匹配状态逻辑关系图Fig.3 Constructed virtual node matching condition logic diagram according to BEset
2.4局部匹配筛选子算法
各计算节点接收到布尔表达式的值后,调用局部匹配筛选子算法RPM对局部匹配集Mi.U进行筛选,获得最终的匹配结果Mi.F。算法的具体过程为:首先对每个收到的布尔等式进行处理,如果X(u,w)=1,则表示w匹配u,将w加入u的匹配集中;然后对P中节点u的局部匹配集中的每个节点w和Ep中的每条边(u,u′),如果u′的局部匹配集中有w的孩子节点且至少有一个孩子节点在u′的匹配集中,那么可以确定w匹配u。筛选操作完成后,各计算节点得到与虚节点相连的那些节点的最终匹配状态,并把匹配结果发送给协调器节点。
3实验与结果分析
3.1disGPM-PE算法与已有分布式算法的比较
根据两个具有典型代表的分布式图匹配算法[4-5]的基本思想设计参考算法并与disGPM-PE算法进行比较。参考算法1(refGPM-1)基于文献[5]算法基本思想,不同计算节点之间仅传送虚节点的匹配信息,当位于不同计算节点上的数据片段之间具有依赖关系时,不作任何优化,多个计算节点根据数据片段之间的依赖关系依次进行图匹配。参考算法2(refGPM-2)基于文献[4]算法基本思想,首先每个计算节点并行地对本地数据进行图模式匹配,然后存储在不同计算节点上的连通子图被发送到一个计算节点上进行组合,最后再对组合后的子图进行图模式匹配。
首先使用默认实验环境配置,模式图中有9个节点,对disGPM-PE算法和两种参考算法进行对比实验。图4为各算法的通信量的比较结果。如图所示,无论是对于Amazon,Google还是合成数据集Synthetic,refGPM-1算法具有最小的通信量,因为使用该算法时,不同计算节点之间仅需要传送边界点的匹配信息。而refGPM-2算法的通信量最大,因为使用该算法时,需要根据数据图的划分情况,将存储在多个计算节点上的连通子图发送到一个计算节点上进行组合。所提出的disGPM-PE算法的通信量介于refGPM-1和refGPM-2算法的通信量之间,因为仅需要在计算节点之间传输布尔等式和虚节点的匹配状态信息,避免传输整个连通子图,因此通信量小于refGPM-2算法的通信量,但是大于refGPM-1算法仅传输边界点的匹配信息所需的通信量。
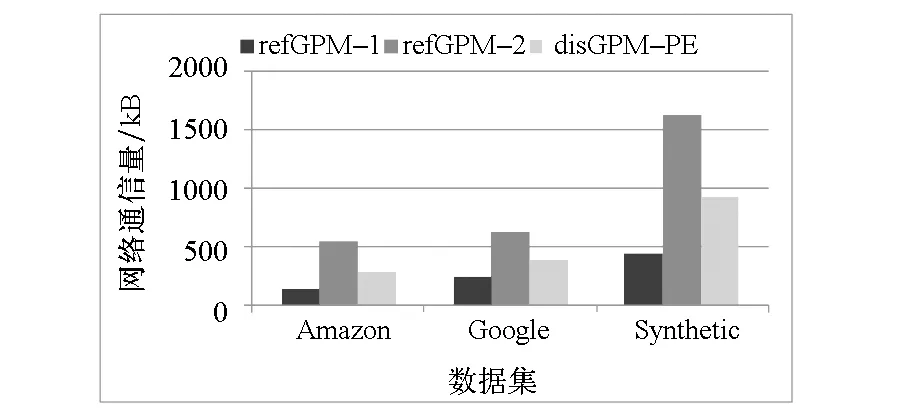
图4 各算法通信量的比较结果Fig.4 Network traffic of different algorithms
图5为disGPM-PE与两种参考算法的执行时间的比较结果。如图5所示,对于三个数据集,refGPM-1算法的执行时间最长,原因是该算法执行过程中多个计算节点根据数据片段之间的依赖关系依次进行图匹配,具有依赖关系的数据片段所在的计算节点不能独立处理这些数据片段,依赖关系越多,并行性越差,执行时间越长。refGPM-2算法和disGPM-PE算法均能够对本地数据并发地进行图模式匹配,refGPM-2算法比disGPM-PE算法的执行时间稍长,因为其通信量较大造成通信时间较长。
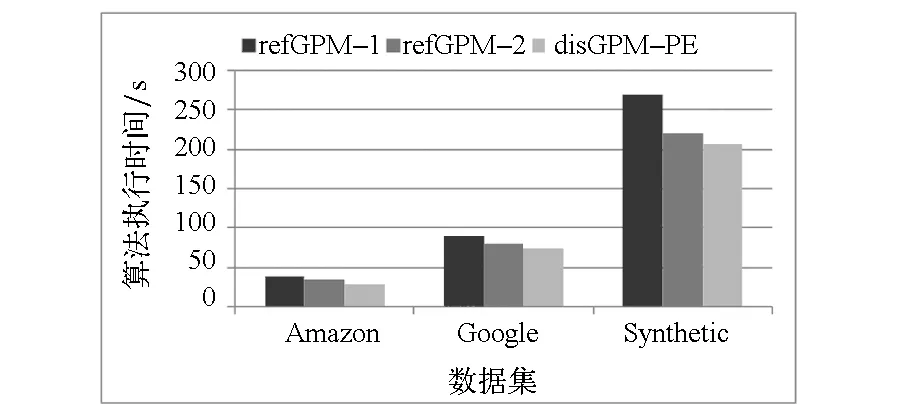
图5 各算法执行时间的比较结果Fig.5 Execution time of different algorithms
分析图4和图5的实验结果发现:refGPM-1算法虽然具有最小的通信量,但是执行时间最长;refGPM-2算法虽然需要更多的通信量,但是却能够节省执行时间;所提出的disGPM-PE算法在具有比refGPM-2算法执行时间稍短的情况下,具有较小的通信量。对于大规模分布式图来说,图匹配算法的执行时间非常重要,通信量也是必须控制的关键指标,所提出的disGPM-PE算法能够在降低执行时间的前提下控制节点间通信量的显著增长。
3.2模式图大小对disGPM-PE执行时间的影响
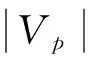
3.3数据图大小对disGPM-PE执行时间的影响

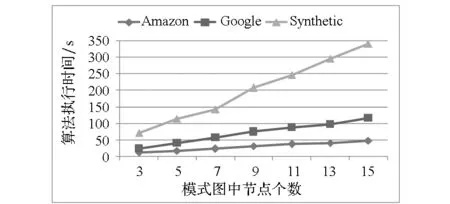
(a) 模式图节点个数对算法执行时间的影响(a) Execution time with different number of pattern graph nodes

(b) 模式图的边密度对算法执行时间的影响(b) Execution time with different edge density of pattern graph
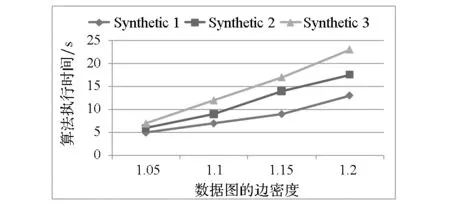
(c) 数据图规模对算法执行时间的影响(c) Execution time with different size of data graph图6 模式图和数据图规模对算法执行时间的影响Fig.6 Effects of the sizes of pattern graph and data graph on the execution time of disGPM-PE
3.4模式图大小对disGPM-PE通信量的影响
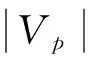
3.5数据图大小对disGPM-PE通信量的影响

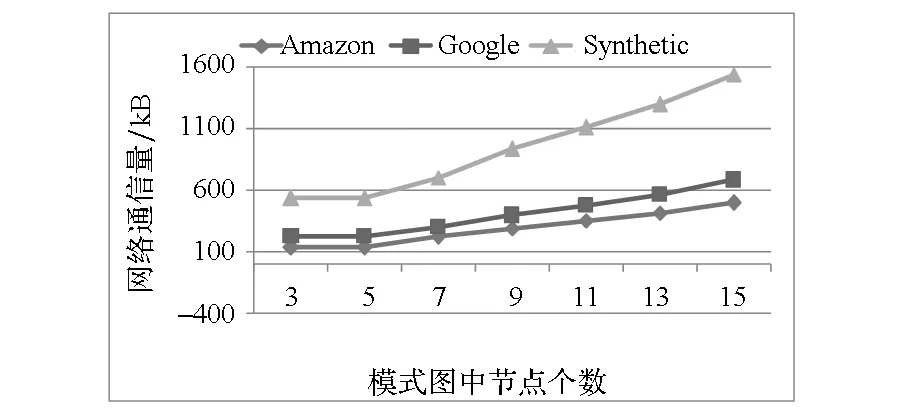
(a) 模式图节点个数对网络通信量的影响(a) Network traffic with different number of pattern graph nodes

(b) 模式图的边密度对网络通信量的影响(b) Network traffic with different edge density of pattern graph

(c) 数据图规模对网络通信量的影响(c) Network traffic with different size of data graph图7 模式图和数据图大小对算法网络通信量的影响Fig.7 Effects of the sizes of pattern graph and data graph on the network traffic of disGPM-PE
4结论
针对分布式大图提出一种基于局部评估的分布式图模式匹配算法disGPM-PE,算法具有不需要明确知道数据是如何分布存储的特点,对图的划分和存储没有任何限制,因此具有更好的适用性。算法通过仅传输布尔等式和虚节点的匹配状态,能够避免部分已有算法由于需要传输连通子图而增加通信量,同时通过协调器节点统一计算虚节点匹配状态,能够在数据片段具有依赖关系时,避免串行进行图模式匹配,因此执行时间不会随依赖关系的增加而增加。实验结果表明,和已有算法相比, disGPM-PE算法能够在降低执行时间的前提下有效控制节点间通信量的显著增长。
参考文献(References)
[1]Gallagher B. Matching structure and semantics: a survey on graph-based pattern matching [C]// Proceedings of AAAI Fall Symposium on Capturing and Using Patterns for Evidence Detection, Boston, USA, 2006: 45-53.
[2]Fan W F, Li J Z, Ma S, et al. Graph homomorphism revisited for graph matching [C]// Proceedings of the 36th International Conference on Very Large Data Bases, Singapore, 2010: 1161-1172.
[3]Liu C, Chen C, Han J W, et al. GPLAG: detection of software plagiarism by program dependence graph analysis[C]// Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, USA, 2006: 872-881.
[4]Ma S, Cao Y, Huai J P, et al. Distributed graph pattern matching[C]// Proceedings of the 21th International World Wide Web Conference, Lyon, France, 2012: 949-958.
[5]Fan W F, Wang X, Wu Y H,et al. Distributed graph simulation: impossibility and possibility [C]// Proceedings of the 40th International Conference on Very Large Data Bases, Hangzhou, China, 2014: 1083-1094.
[6]Frad A, Nisar M U, Ramaswamy L, et al. A distributed vertex-centric approach for pattern matching in massive graphs [C]// Proceedings of IEEE International Conference on Big Data, Santa Clara Marriott, CA, USA, 2013: 403-411.
[7]Fan W F, Wang X, Wu Y H. Performance guarantees for distributed reachability queries[C]// Proceedings of the 38th International Conference on Very Large Data Bases, Istanbul, Turkey, 2012: 1304-1315.
[8]Stanford University. Stanford large network dataset collection[EB/OL] (2014-01-15)[2014-04-10]. http://snap.stanford.edu/data/index.html.
[9]Dean J, Ghemawat S. Mapreduce: simplified data processing on large clusters [C]// Proceedings of the 6th Symposium on Operating Systems Design and Implementation, San Francisco, USA, 2004.
[10]Malewicz G, Austern M H, BikA J C, et al. Pregel: a system for large-scale graph processing [C]// Proceedings of International Conference on Management of Data, Indianapolis, Indiana, 2010: 135-145.
doi:10.11887/j.cn.201602013
*收稿日期:2015-03-27
基金项目:国家自然科学基金资助项目(61232001,61173169);湖南省教育厅资助项目(15C0824)
作者简介:张丽霞(1979—),女,河南周口人,讲师,博士研究生,E-mail:smilingilsa6@163.com;王伟平(通信作者),女,教授,博士,博士生导师,E-mail:wpwang@csu.edu.cn
中图分类号:TP311
文献标志码:A
文章编号:1001-2486(2016)02-075-07
A distributed graph pattern matching algorithm using partial evaluation
ZHANG Lixia1, 2, WANG Weiping1, GAO Jianliang1, WANG Jianxin1
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;2. School of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China)
Abstract:In order to execute graph pattern matching quickly in distributed large-scale graphs, an effective distributed algorithm using partial evaluation, namely disGPM-PE was proposed. Firstly, partial matching was performed locally at each computer nodes in parallel. Secondly, a coordinator node assembled the partial matching results, evaluated and sent the matching conditions of boundary nodes to corresponding computer nodes. Thirdly, each computer nodes determines the matching conditions of the nodes connected to the boundary nodes. Finally, the maximum matching set was collected at the coordinator node. Experiment results show that the disGPM-PE algorithm can avoid the impact of the dependent relations between data fragments on the execution time. Compared with the previous distributed graph pattern matching algorithms, the disGPM-PE algorithm can reduce the execution time of graph pattern matching while do not increase the network traffic obviously.
Key words:graph pattern matching; distributed algorithms; partial evaluation
http://journal.nudt.edu.cn

