横向扰动对超声速混合层被动标量混合影响分析*
冯军红,沈赤兵
(1.国防科技大学 航天科学与工程学院, 湖南 长沙 410073;2.高超声速冲压发动机技术重点实验室, 湖南 长沙 410073)
横向扰动对超声速混合层被动标量混合影响分析*
冯军红1,2,沈赤兵1,2
(1.国防科技大学 航天科学与工程学院, 湖南 长沙410073;2.高超声速冲压发动机技术重点实验室, 湖南 长沙410073)
摘要:采用大涡模拟数值计算二维空间发展的超声速混合层,重点分析横向扰动对混合层的标量结构、标量厚度以及标量体积卷吸率的影响。采用理论模型验证了数值方法在计算标量混合特性方面的准确性。结果表明,横向扰动频率和振幅明显影响着混合层的标量增长率和卷吸率。高频扰动增大了混合层近场标量增长率和卷吸率,但是低频扰动改善了混合层远场标量增长率。大尺度涡卷吸过程对混合层标量卷吸率起决定作用。多频扰动有效地增强了超声速混合层的标量混合。
关键词:横向扰动;超声速混合层;被动标量;动量比;卷吸率
随着超燃冲压发动机技术及组合循环发动机技术的发展,超声速混合层再次受到研究者的密切关注[1-4]。 在发动机燃烧室内,高速空气与富燃燃气或燃料高速掺混与燃烧,同时确保总压沿程损失最小。但是,超声速空气在有限尺寸的燃烧室内的驻留时间是毫秒级的,且燃料与空气的混合效率随着压缩性的增长而显著下降。如何在非常短的时间内达到空气与燃料的充分混合以提高燃烧效率是急需解决的一个难题。因此,以燃烧室内基本流动与混合为模型的超声速混合层为研究对象,开展混合层标量场的输运和混合特性的研究对于改善混合与燃烧效率具有指导意义。
相对于可压缩混合层的动量场的研究,超声速混合层的标量场研究较少。早期,Clemens和Mungal[5]实验研究了不同对流马赫数的平板混合层的标量结构,采用No-PLIF测量了标量场。实验结果表明,当对流马赫数小于0.6时,超声速混合层呈二维标量结构;但当对流马赫数大于0.6时,标量结构呈现三维特性。Miller 等[6]研究了压缩性对反应混合层内的组分分布的影响,认为对流马赫数改变了混合组分的空间分布特征。随后,Sankaran[7]和Ribault[8]采用大涡模拟方法数值计算了可压缩混合的被动标量过程,认为数值模型(亚格子应力模型)以及数值方法对计算结构有较大的影响。国内赵玉新[9]研究了超声速混合层的涡特性,并获得精细涡结构。孙明波[10]和薛淑艳[11]等开展了超声速混合层被动标量的混合过程研究。最近,陈军等[12-14]实验研究了可压缩混合层,并采用新的数据提取方法获得了混合层的多尺度涡特性和厚度增长特性。但是,上述研究未能详细分析混合层被动标量增长特性和卷吸特性。
运用大涡模拟方法,数值计算了二维超声速混合层被动标量混合过程,并研究了上游扰动频率及振幅对混合层标量增长特性与卷吸特性的影响规律。
1数值模拟方法
经过Favre平均的Navier-Stokes方程可得到大涡模拟控制方程,具体的控制方程可见文献[15]。针对亚格子应力项,采用一方程模型进行封闭。
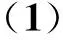

为捕捉标量结构和标量组分分布,将上下两股空气来流标记成不同的组分,通过求解组分质量分数方程获得标量组分的分布。经过Favre过滤后的标量输运方程为:
控制方程的对流项采用5阶加权本质无振荡(Weighted Essentially Non Oscillatory, WENO)格式求解,黏性项采用二阶中心差分格式,时间推进采用3阶Runge-Kutta方法。库朗数取为0.5。混合层入口直接给定超声速入口条件(可见2.1节),出口采用直接外推的方法,上下两股来流边界采用非反射边界条件。
2计算结果与验证
2.1计算对象
所模拟的二维空间发展的超声速混合层的来流参数可见表1,上下两股来流马赫数表示为M1和M2,来流静压为P0。计算得到混合层的来流速度U1=623.21 m/s和U2=518.19 m/s,对流马赫数Mc=(U1-U2)/(a1+a2)=0.21,式中a1和a2是来流声速。混合层雷诺数是基于初始涡厚度和速度差计算的。值得注意的是,本文计算工况的对流马赫数较小,混合层仍以二维结构为主[5],这也说明采用二维大涡模拟方法是有效的。
入口速度剖面为双曲正切函数:

(3)
其中,δω(0)为初始涡厚度,入口温度分布按照Busemann-Crocco定律计算。为有效促进混合层失稳,需要在入口处添加一定的扰动。这里在入口的纵向速度分量υ引入扰动速度,即添加一种横向扰动,其形式为:
(4)
其中,G(y)是Gauss函数,Am是m谐波的扰动振幅,fm是m谐波的扰动频率,则m谐波的相位为φm。对于单频扰动,则n=m=1。
计算域为Lx×Ly,其中Lx/L=800,Ly/L=120,L为初始标量厚度。网格精度为Nx×Ny=1340×415。纵向网格以双曲正切函数在混合区内加密,流向网格分布均匀。针对所研究的空间尺度和雷诺数,计算网格尺度足以精确捕捉流场标量结构[10-11]。
2.2计算工况验证
在实际流动中,混合层入口总是带着各种随机扰动。为真实模拟自然发展的混合层,基准工况下的混合层入口处添加小幅随机扰动(扰动频率是103Hz和106Hz的均匀随机量,扰动振幅A1=0.08Uc,则相位角等于0°)。计算得到的混合层涡量场与标量场如图1所示。在随机扰动下,混合层Kelvin-Helmholtz失稳,大尺度展向涡逐渐卷起、对并。在涡卷吸过程中,标量界面逐渐变形、拉伸,且标量有效地掺混形成一些大尺度标量结构,这说明被动标量输运与混合受到混合层大尺度涡动力特性影响。此外,由于上游随机扰动,导致混合层涡随机卷起和随机对并,形成一系列不同尺度的涡与标量结构。图2对比了本文计算获得的归一化速度和均方根(Root Mean Square, RMS)与已有的实验结果[16-17],图中无量纲横向坐标η=(y-ycl)/b,其中b为混合层当地涡厚度,ycl是归一化速度为0.5的混合层纵向位置。计算得到的归一化流向速度较好地吻合前人的实验结果,且不同流向位置的速度曲线基本重合,说明混合层一阶速度量已达到自相似状态。横向速度均方根处于预先的实验数据内,但在峰值处仍有一些误差,原因可能是计算与实验工况的来流参数存在略微差异,比如雷诺数等。但计算结果仍能准确预测混合层速度场,说明本文采用的方法可合理捕捉流场大尺度涡结构。

图1 基准工况下的混合层涡量场与标量场Fig.1 Vorticity and scalar contours for baseline case
为验证基准工况的混合层标量特性计算结果的准确性,标量的空间增长率和体积卷吸率作为验证参数用于对比仿真结果与理论模型结果。超声速混合层的空间增长率可通过式(5)~(6)进行理论估计[18-19]:
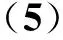
f(Mc)=0.8e-3Mc2+0.2
(6)
其中,r=U2/U1,s=ρ2/ρ1,Cδ=0.25~0.45。
不可压缩混合层的体积卷吸率的理论计算可表示为:
(7)
式中,Ve1表示混合层卷吸上层来流的体积量,Ve2表示混合层卷吸下层来流的体积量。对于压缩性混合层,为准确计算混合层体积卷吸率,体积卷吸率进行了密度加权,即:
(8)
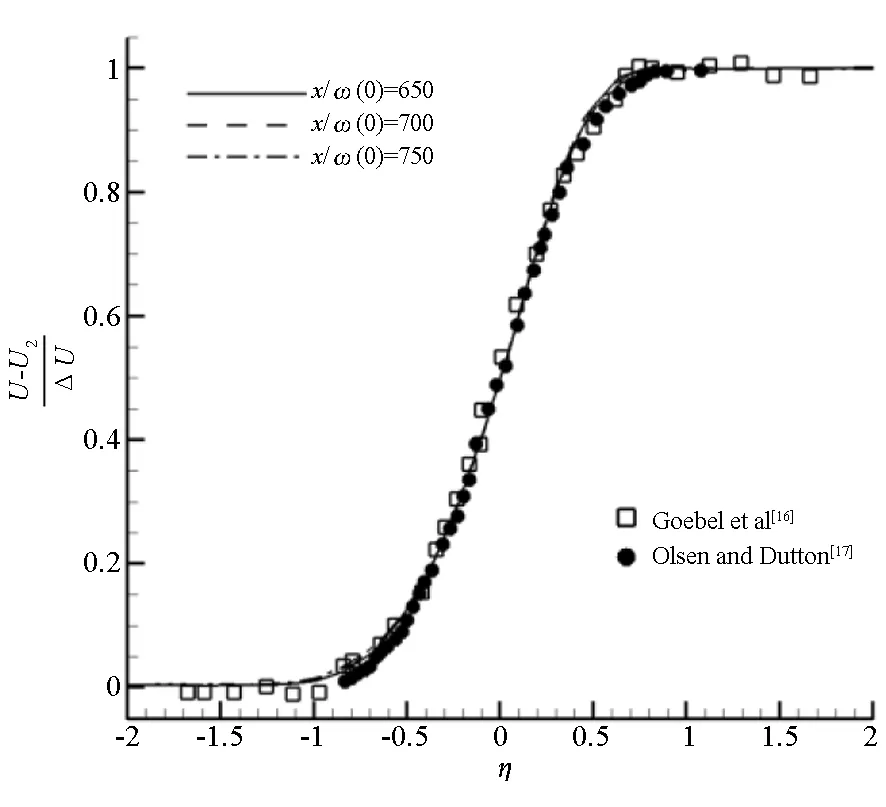
(a)归一化流向速度(a) Normalized streamwise velocities
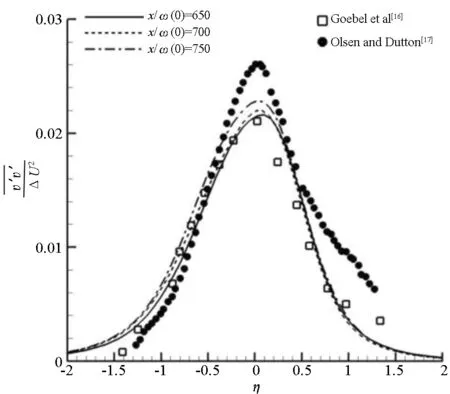
(b)横向速度的均方根 (b) RMS of transverse velocity图2 计算结果与已有实验数据对比图Fig.2 Comparisons of numerical results with previous data
数值计算中,混合层标量的空间增长率与卷吸率计算示意图如图3所示,图中Y是标量的质量分数。δ(x)是标量厚度,根据图3所示,标量厚度可根据式(9)计算:
δ(x)=y(Y1=0.1)-y(Y1=0.9)
(9)
则厚度增长率计算为:
(10)
标量的体积卷吸率可通过式(11)计算[20]:
(11)
对于空间位置某一段的平均体积卷吸率为:
(12)

图3 混合层标量增长率与卷吸率计算示意图Fig.3 Schematic of the scalar calculation of the spatial growth rate and the entrainment ratio in mixing layer
图4所示为基准工况下混合层的标量厚度和体积卷吸率沿流向变化曲线。随机扰动的混合层

(a)标量厚度(a) Scalar thickness
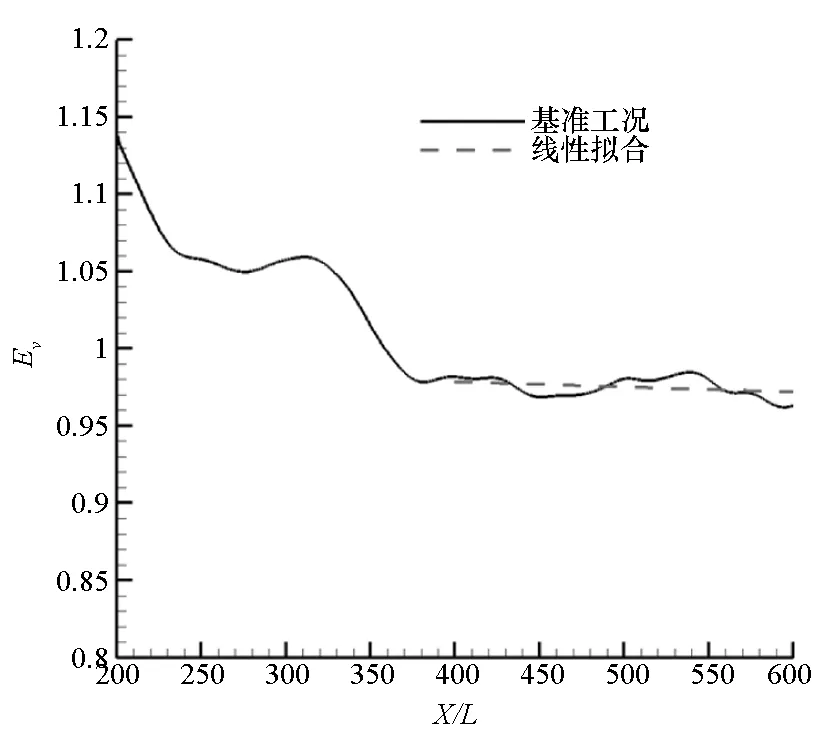
(b)体积卷吸率(b)Volumetric entrainment ratio图4 基准工况的标量厚度增长和卷吸率沿流向分布曲线Fig.4 Variation of scalar thickness and volumetric entrainment ratio with downstream distance
经过初始段的发展后,进入了准线性增长阶段。标量厚度增长曲线可通过线性曲线完美拟合,如图4(a)所示,从而可求得基准工况混合层的标量增长率。同时,混合层的体积卷吸率在准线性增长阶段逐渐衰减,这说明混合层呈现非对称的卷吸。在初始阶段混合层高速侧的卷吸量较大,但是随着向下游发展,低速侧的卷吸量逐渐增大,并大于高速侧,从而导致混合层卷吸率小于1。这是由于高速侧的来流动量大于低速侧,导致混合层向低速侧倾斜[20]。此外,在准线性增长阶段,混合层的卷吸率逐渐趋于一定值。
表2所示为混合层准线性增长阶段(X/L=200~500)内的标量增长率和卷吸率数值结果与理论结果的对比值。其中理论计算的增长率系数Cδ=0.4,数值计算得到的标量增长率和卷吸率几乎符合理论值。这说明本文采用的计算方法可有效地捕捉混合层标量输运特性。
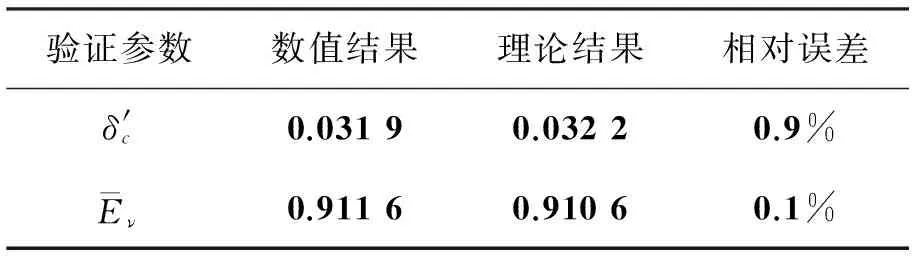
表2 验证参数
3扰动频率对被动标量混合的影响
为研究横向扰动频率对混合层标量混合的影响,在横向速度上添加不同频率的扰动,其中n=m=1,f1=F=5.96×104Hz,其中f1是基准工况的混合层在准线性增长阶段起始位置的最不稳定频率。振幅固定不变A1=0.08Uc,相位角φ1=0。图5所示为单频扰动下混合层的标量结构。混合层初始卷涡结构受到上游扰动频率的控制,在单频扰动下,混合层涡逐渐卷起,发展最终达到饱和状态。在低频扰动下,混合层需较长距离达到饱和状态,但是饱和涡尺度较大。随着扰动频率的增大,混合层迅速卷涡,并在较短的距离内达到饱和状态,但是饱和涡尺度较小。此外,在低频作用下,卷涡结构的“辫子”区域诱发小尺度涡结构,这些小涡结构“骑”在大尺度的拟序结构上。这是由于入口数值振荡引起的高频扰动诱发的小尺度结构。但在高频激励下,这些小尺度结构消失,显然是因为高频扰动对其他小扰动具有抑制作用。这说明扰动频率可控制混合层的涡动力学特性,从而用于流动控制。

图5 不同频率扰动下混合层的标量结构Fig.5 Scalar structures for forced mixing layers with different forcing frequencies

(a)标量厚度(a) Scalar thickness
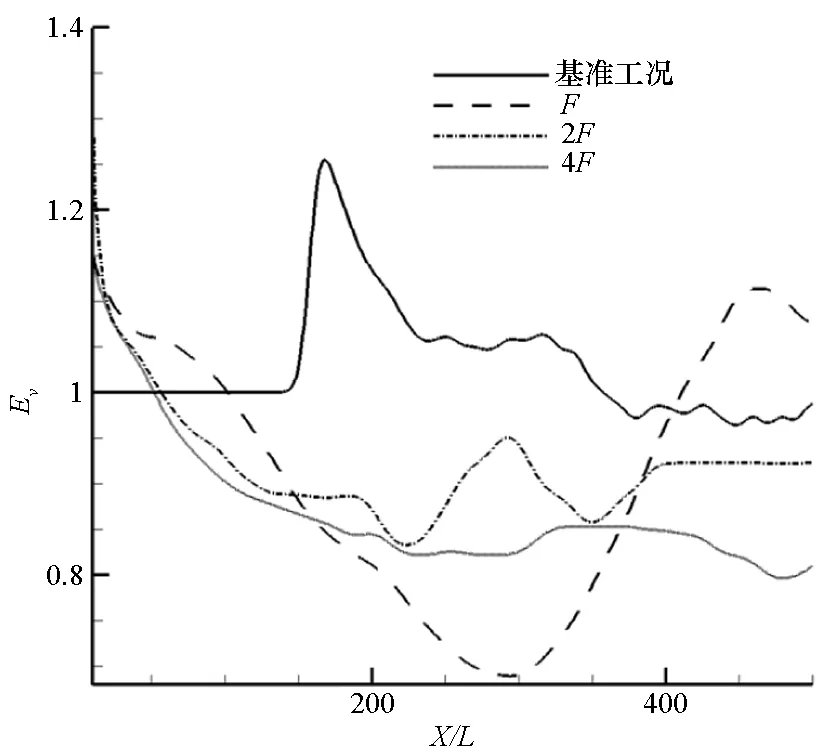
(b)体积卷吸率(b) Volumetric entrainment ratio图6 不同频率作用下混合层的标量厚度和体积卷吸率沿流向变化曲线Fig.6 Variation of scalar thickness and volumetric entrainment ratio with downstream distance for different forcing frequencies
不同频率作用下的混合层标量厚度和体积卷吸率沿流向变化如图6所示。相对于基准工况,受扰动的混合层呈现非线性发展模式。这一计算结果与文献[14]获得的结论吻合,文献[14]通过实验测量发现混合层呈现非线性增长特性,并认为这一非线性特性与来流入口扰动相关。在单频激励下,标量厚度在初始阶段迅速增长,显然扰动频率明显增大了混合层近场的标量增长率。这也是由于扰动频率改变了混合层近场涡动力学特性。在大尺度涡卷吸作用下,标量厚度迅速增长。同时,扰动频率越高,近场的标量厚度增长越快。这是由于高频激励下拟序结构迅速卷起,增大了近场的标量增长率。但是,随着拟序结构趋于饱和,标量厚度逐渐趋于平缓。在平缓阶段,低频扰动的标量厚度明显大于高频激励,这是由于低频诱发的大尺度涡尺度明显大于高频扰动。
同样地,扰动频率也影响着混合层的体积卷吸率。图6(b)所示为不同频率的体积卷吸率,值得注意的是,在基准工况的过渡段(图6(a)所示的X/L=0~150),由于较薄的标量厚度,基准工况的混合层标量的体积卷吸率未能准确捕捉,这里统设为1。可看出,相对于基准工况,受扰动的混合层在大尺度涡诱导下,迅速卷吸外围流体,引起卷吸率迅速下降。扰动频率越高,体积卷吸率衰减越快,这说明混合层向下倾斜。随着向下游发展,由于低频诱发的大尺度涡结构逐渐主导标量卷吸过程,低频扰动下的体积卷吸率衰减量最大,同时波动也最大。随后,混合层达到中性稳定状态,拟序结构趋于饱和,体积卷吸率变化缓慢。这说明混合层的初始涡卷起过程极大地影响着体积卷吸率。
4扰动振幅对被动标量混合的影响

(a)标量厚度(a) Scalar thickness
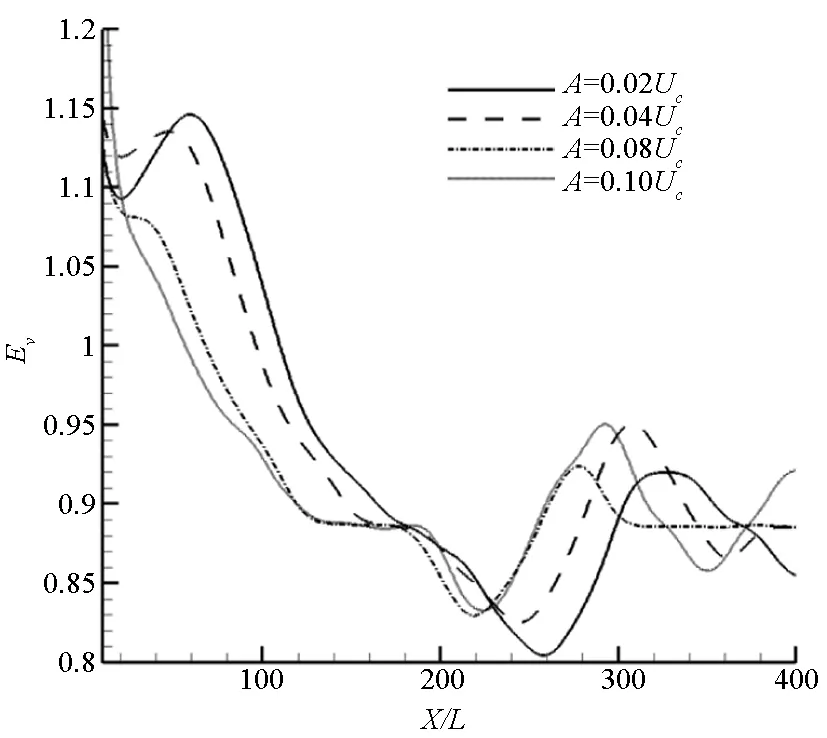
(b)体积卷吸率(b) Volumetric entrainment ratio图7 不同振幅作用下混合层的标量厚度和体积卷吸率沿流向变化曲线Fig.7 Variation of scalar thickness and volumetric entrainment ratio with downstream distance for different forcing amplitudes
给定固定的扰动频率f1=5.96×104Hz,通过改变上游扰动振幅以研究振幅对被动标量混合的影响。图7给出了不同扰动振幅下混合层标量厚度和体积卷吸率沿流向变化曲线。同样地,在单频扰动下,标量厚度由于混合层初始阶段涡卷作用迅速增大,当卷涡结构逐渐饱和时,标量厚度逐渐趋于一定值。而且不同幅值扰动下标量厚度趋于同一定值,这说明扰动振幅对饱和涡尺度没有影响。扰动振幅只改变混合层初始段的涡卷过程,幅值越大,混合层越早起涡,从而标量厚度增长较快。这进一步说明扰动振幅可以促进涡卷快速形成,从而提高了初始段的标量厚度增长率。由于扰动振幅影响着涡卷的形成过程,因而也影响着混合层的体积卷吸率。涡卷起越早,体积卷吸率衰减越快,说明混合层发展越快。说明涡卷过程同样影响着混合层的卷吸过程。
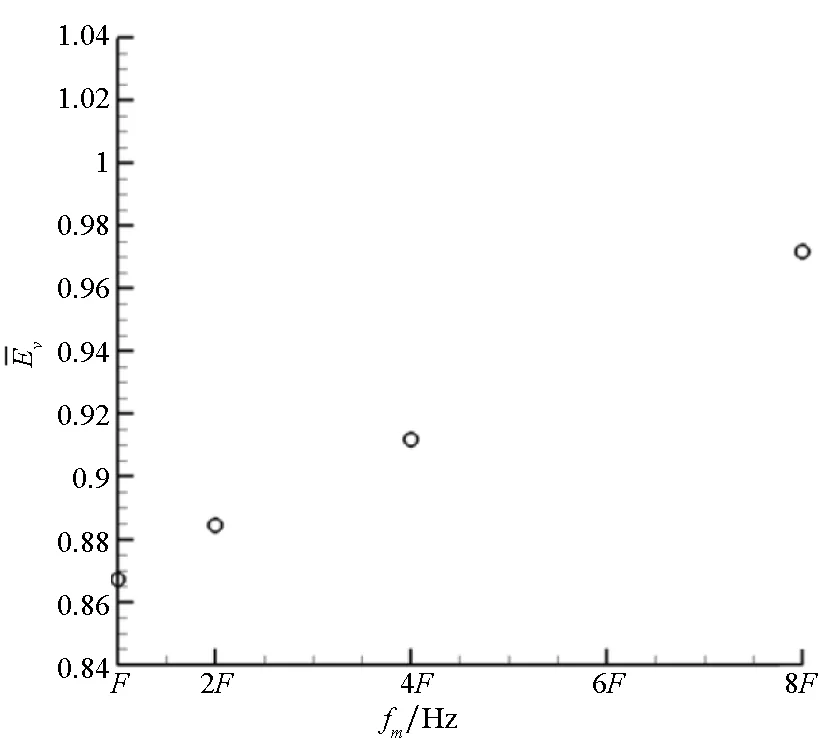
为进一步分析涡卷过程对标量体积卷吸率的影响,计算了涡卷阶段的标量平均卷吸率,即从起涡到涡达到饱和这一阶段的平均体积卷吸率。图8所示了涡卷阶段的不同频率(对应于上文的单频扰动工况)和振幅(频率不变)的平均体积卷吸率。扰动频率越高,这一阶段的平均卷吸率越大。这说明涡尺度在混合层卷吸过程起主导作用,增强了标量混合。扰动振幅越大,涡卷阶段的平均卷吸率越小,这说明在涡尺度相同下,涡卷起越快,标量混合越快。但是振幅增大到一定程度,其影响作用并不明显。
(a) 扰动频率(a) Forcing frequency
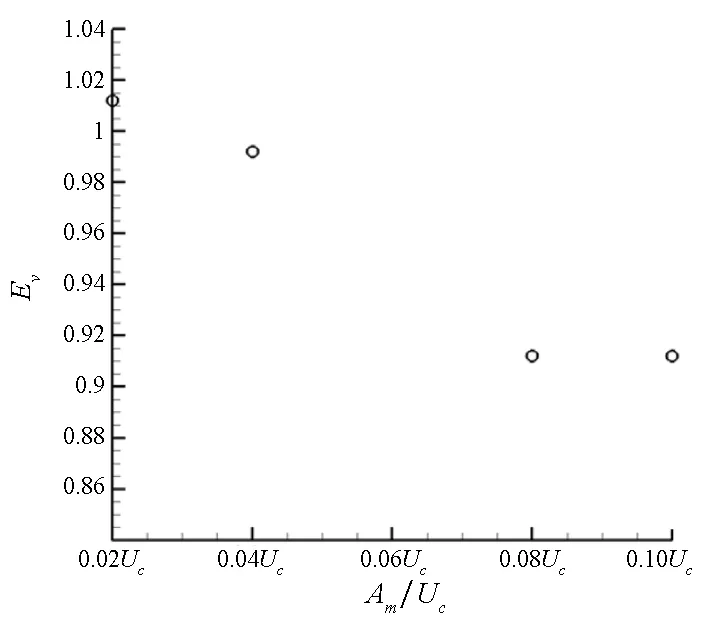
(b) 扰动振幅(b) Forcing amplitude图8 涡卷阶段的标量平均卷吸率随扰动频率和振幅变化图Fig.8 Mean volumetric entrainment ratiochanging with the forcing frequency and amplitude during the rollup stage
5多频扰动对混合层被动标量混合的影响
多频扰动下,混合层出现了涡并或者涡撕裂现象。为研究涡并对标量混合的影响,将双频(F+2F)或三频(F+2F+4F)扰动同时添加在混合层入口。图9所示为双频扰动下混合层涡卷阶段和涡并阶段的标量结构图。在涡卷阶段,在两种频率扰动下,两种不同尺度的涡结构形成。随着混合层向下游发展,亚谐扰动控制的涡结构逐渐饱和,随着两个涡逐渐靠近,涡并发生,混合层进入涡并阶段。涡并完成后,更大尺度的涡结构形成,并向下游发展。
图10所示为多频作用下标量厚度沿流向的变化曲线。多频扰动明显增大了标量厚度,这是由于高频作用下,混合层快速起涡,引起标量厚度的迅速增大。随着涡并的发生,标量厚度进一步增大。这说明,在混合层发展初始阶段,涡卷作用控制着标量混合,在混合层向下游发展,涡并作用主导着标量混合,在单频扰动下,混合层并未产生涡并,引起标量厚度增长逐渐下滑。

图9 混合层涡卷阶段和涡并阶段的标量结构图Fig.9 Scalar structures during the rollup stage and vortex pairing stage
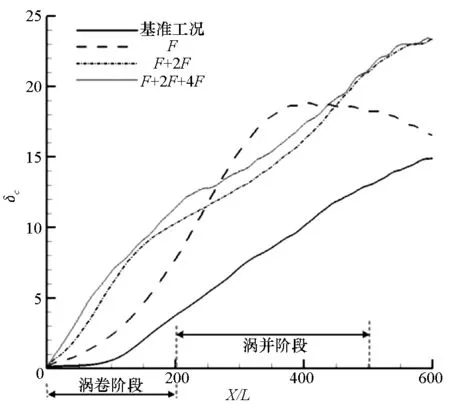
图10 多频扰动下混合层标量厚度沿流向变化曲线Fig.10 Variation of scalar thickness with downstream distance for multiple-frequency forcing
6结论
应用大涡模拟数值方法研究了二维空间发展超声速混合层的被动标量混合特性,重点分析了横向扰动对标量结构、标量厚度增长以及标量卷吸率的影响规律,并验证了仿真结果。得出了以下的结论:
1)数值计算获得的标量厚度增长率和卷吸率符合理论值,说明所采用的计算模型与方法可有效捕捉标量混合特性。
2)横向扰动可以明显地改善混合层的标量厚度增长特性。这是由于扰动控制着混合层近场大尺度涡的动力学特性。而涡的卷吸与演化直接影响着标量增长与卷吸特性。在横向扰动作用下,混合层标量厚度呈现非线性增长特性。
3)高频扰动可以提高混合层初始阶段的标量增长率,但是低频扰动可以明显增大远场的标量厚度。扰动振幅只影响混合层的近场标量增长率。
4)混合层的大尺度涡结构决定着标量卷吸率,混合层涡尺度越大,混合层越向低速侧倾斜,卷吸率越小。混合层的涡卷和涡并阶段是卷吸率变化最为剧烈的阶段。
5)多频扰动可以明显提高混合层近场与远场的标量增长率。
参考文献(References)
[1]Segal C. The scramjet engine processes and characteristics[M]. New York:Cambridge University Press, 2009.
[2]McDaniel J C, Chelliah H, Goyne C P. US national center for hypersonic combined cycle propulsion: an overview [C]//Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, AIAA 2009-7280, 2009.
[3]Ground C, Zhu W B, Maddalena L. Design of a model scramjet combustor for vortex-enhanced mixing and combustion studies [C]//Proceedings of the 19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, AIAA 2014-2952, 2014.
[4]李平, 李文龙, 何国强. 空气涡轮火箭发动机内外涵气流掺混研究[J]. 固体火箭技术, 2012, 35(1): 47-52.
LI Ping, LI Wenlong, HE Guoqiang.Research on turbulent mixing of the bypass and core flows for air-turbo-rocket[J]. Journal of Solid Rocket Technology, 2012, 35(1): 47-52. (in Chinese)
[5]Clemens N T, Mungal M G. Large scale structure and entrainment in the supersonic mixing layer [J]. Journal of Fluid Mechanics, 1995, 284: 171-216.
[6]Miller M F, Bowman C T, Mungal M G. An experimental investigation of the effects of compressibility on a turbulent reacting mixing layer [J]. Journal of Fluid Mechanics, 1998, 356: 25-64.
[7]Sankaran V, Genin F, Menon S. Sub-grid mixing model for large eddy simulation of supersonic combustion [C]//Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2004-0801, 2004.
[8]Le Ribault C. Large eddy simulation of passive scalar in compressible mixing layers [J].International Journal of Heat and Mass Transfer, 2008, 51(13/14): 3514-3524.
[9]赵玉新, 易仕和, 何霖, 等. 超声速湍流混合层中小激波结构的实验研究[J]. 国防科技大学学报, 2007, 29(1): 12-15.
ZHAO Yuxin, YI Shihe, HE Lin, et al. The experimental research of shocklet in supersonic turbulent mix layer [J]. Journal of National University of Defense Technology, 2007, 29(1): 12-15. (in Chinese)
[10]孙明波, 王振国, 梁剑寒.入流周期性温度激励下的二维超声速混合层混合增强[J]. 宇航学报, 2008,29(2): 444-448.
SUN Mingbo, WANG Zhenguo, LIANG Jianhan. Mixing enhancement of a 2D supersonic mixing layer induced by inflow periodic temperature excitation [J]. Journal of Astronautics, 2008, 29(2): 444-448. (in Chinese)
[11]薛淑艳, 张会强, 王希麟. 超音速平板混合层被动标量的数值模拟[J]. 工程热物理学报, 2009, 30(8): 1423-1426.
XUE Shuyan, ZHANG Huiqiang, WANG Xilin. Numerical simulation of passive scalar in supersonic planar mixing layers[J]. Journal of Engineering Thermophysics, 2009, 30(8): 1423-1426. (in Chinese)
[12]Wang T J, Shi X T, Chen J, et al. Multi-scale structures in compressible turbulent mixing layers [J]. Modern Physics Letters B2, 2010, 24(13): 1429-1432.
[13]Chen J, Shi X T, Wang T J, et al. Wavy structures in compressible mixing layers [J]. Acta Mechanica Sinica, 2013, 29(5): 633-640.
[14]Wang T J, Chen J, Shi X T, et al, Experimental evidence for non-linear growth in compressible mixing layer [J]. Science China, Physics, Mechanics & Astronomy, 2014, 57(5): 963-970.
[15]Wang H B, Qin N, Sun M B, et al. A dynamic pressure-sink method for improving large eddy simulation and hybrid Reynolds-averaged Navier-Stokes/large eddy simulation of wall-bounded flows [J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2012, 226(9): 1107-1120.
[16]Goebel S G, Dutton J C, Krier H, et al. Mean and turbulent velocity measurements of supersonic mixing layers [J]. Experiments in Fluids, 1990, 8(5): 263-272.
[17]Olsen M G, Dutton J C.Stochastic estimation of large structures in an incompressible mixing layer [J]. AIAA Journal, 2002, 40(12): 2431-2438.
[18]Dimotakis P E. Turbulent free shear layer mixing and combustion [C]//Proceedings of the 9th International Symposium on Air Breathing Engines,GALCIT Report FM91-2, 1989: 58-79.
[19]Nuding J R.Interaction of compressible shear layers with shock waves: an experimental study, Part I [C]//Proceedings of International Space Planes and Hypersonic Systems and Technologies Conferences,AIAA 1996-4515, 1996.
[20]Soteriou M C, Ghoniem A F. Effects of the free-stream density ratio on free and forced spatially developing shear layers [J]. Physics of Fluids, 1995, 7(8): 2036-2051.
doi:10.11887/j.cn.201602009
*收稿日期:2015-09-24
基金项目:国家自然科学基金资助项目(11272351,11572346)
作者简介:冯军红(1987—),男,山西临汾人,博士研究生,E-mail:564771857@163.com; 沈赤兵(通信作者),男,研究员,博士,博士生导师,E-mail:cbshen@nudt.edu.cn
中图分类号:V435.12
文献标志码:A
文章编号:1001-2486(2016)02-048-08
Effect of transverse forcing on passive scalar mixing in supersonic mixing layer
FENG Junhong1,2, SHEN Chibing1,2
(1.College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China;2.Science and Technology on Scramjet Laboratory, Changsha 410073, China)
Abstract:Numerical studies on a spatially developing supersonic mixing layer were performed by means of large-eddy simulation. Focusing on the effect of transverse forcing on the passive scalar mixing characteristic of mixing layer. The results for the baseline case without external forcing are in agreement with the analytical evidence. Afterwards, the effect of transverse forcing on the scalar structure, scalar thickness and volumetric entrainment ratio of mixing layer were analyzed. Results indicate that the frequency and amplitude of transverse forcing alter the growth rate and entrainment ratio of the passive scalar mixing significantly. High-frequency forcing magnifies the scalar thickness and volumetric entrainment ratio in the near field of mixing layer. However, the growth rate in the far field is increased by the low-frequency forcing. The entrainment ratio is, to be a large extent, dominated by the large-scale eddy entrainment process. The multiple-frequency forcing seems to validly enhance the scalar mixing in supersonic mixing layer.
Key words:transverse forcing; supersonic mixing layer; passive scalar; momentum ratio; entrainment ratio
http://journal.nudt.edu.cn

