混合离子的沉淀准确滴定

乔成立

（齐齐哈尔大学应用技术学院，黑龙江齐齐哈尔161006）



混合离子的沉淀准确滴定

乔成立*

（齐齐哈尔大学应用技术学院，黑龙江齐齐哈尔161006）

摘要：用沉淀滴定的林邦滴定曲线方程推导滴定突跃的绝对值，用滴定突跃的绝对值推导混合离子准确滴定的条件。

关键词：沉淀滴定；滴定突跃的绝对值；混合离子的准确滴定

在滴定分析中，准确滴定既是教学重点，又是教学难点，因此很多教材［1－3］用大量的篇幅讨论准确滴定的问题。对于混合离子的沉淀滴定，文献［1］第275页“混合离子的沉淀滴定”认为：在沉淀滴定中，两种混合离子能否准确进行分别滴定，决定于两种沉淀的溶度积常数比值的大小。例如，用AgNO3滴定I－和Cl－

的混合离子溶液时，首先达到AgI的溶度积而析出沉淀，当I－

定量沉淀以后，随着Ag+浓度升高而析出AgCl沉淀，在滴定曲线上出现两个明显的突跃。当Cl－开始沉淀时，I－和Cl－浓度的比值为：

即当I－浓度降低至Cl－浓度的千万分之五时，开始析出AgCl沉淀。

因为文献［1］只给出结论，没有推导过程，所以学生只能按照混合离子配位分别准确滴定的条件去理解混合离子沉淀分别准确滴定的条件。然而，沉淀滴定与配位滴定不同。因为配位滴定产物的浓度是变量，沉淀滴定产物的浓度是常量。在同浓度滴定的前提下，配位滴定的两种混合离子能否分别准确滴定，只取决于两种配合物形成常数的比值大小［1－3］，而沉淀滴定的两种混合离子能否分别准确滴定，不仅取决于两种沉淀溶度积常数的比值大小，还取决于沉淀溶度积小的被测物质的浓度大小。

为此，本文建立了滴定突跃绝对值的概念，用滴定突跃绝对值定量地说明影响滴定突跃大小的因

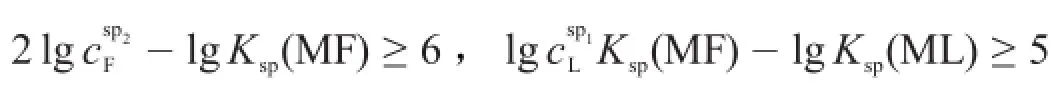
可见，在混合离子的沉淀滴定中，两种混合离子能否分别准确滴定，不仅取决于两种沉淀溶度积常数的比值大小，还取决于沉淀溶度积小的被测物质的浓度大小。

1　滴定突跃的绝对值

1.1副反应系数及条件稳定常数

可见，第一化学计量点时是M滴定混合阴离子（L和F）溶液，第二化学计量点时是M滴定单一阴离子（F）溶液。

如果用αM1（F）表示第一化学计量点时M与F反应的副反应系数，则αM1（F）表示未与L结合的M的总浓度

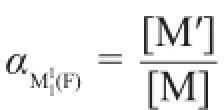
由于沉淀反应有异相生成，当反应物浓度的乘积等于溶度积时，没有沉淀生成。当反应物浓度的乘积大于溶度积时，有沉淀生成，此时沉淀物质的活度就被指定为1，并且不再改变。由于滴定开始至反应物浓度的乘积等于溶度积，没有沉淀生成时，生成物的浓度很小，所以可以忽略。

如，用0.1 mol·L－1AgNO3滴定同浓度的I－和Cl－混合溶液。第一化学计量点时，Ag+的平衡浓度为：

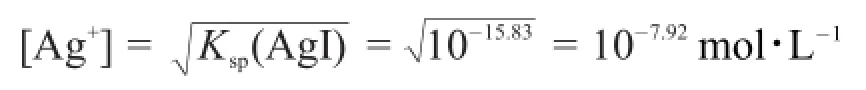
副反应有AgCl沉淀生成需要Ag+的平衡浓度为：

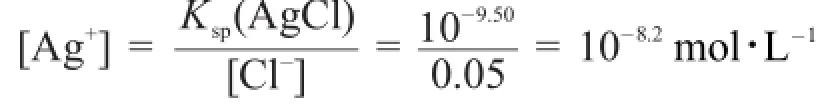
可见，第一化学计量点时，有AgCl沉淀生成。所以，AgNO滴定同浓度的I－和Cl－混合溶液，没有

3AgCl沉淀生成时，生成物AgCl的浓度很小，可以忽略。

因此，我们只讨论副反应的反应物M和F浓度的乘积大于MF的溶度积、有MF沉淀生成时的副反应系数和条件溶度积常数。

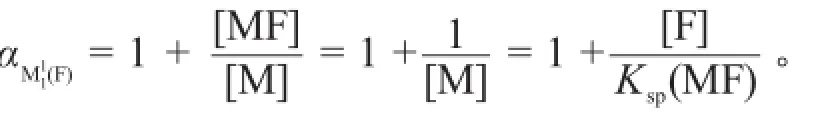
因为csp1=［F］+［MF］，在F和M反应的量较小时，csp1=［F］+［MF］≈［F］，所以第一化学计量点

FF时，M与F反应的副反应系数为：

因为第一化学计量点时，滴定主反应有ML沉淀生成，所以［ML］=1，而且副反应的反应物M和F浓度的乘积大于MF的溶度积，有MF沉淀生成，且［MF］=1，所以：

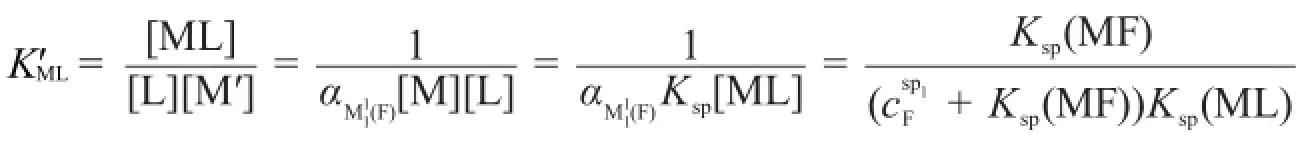
所以第一化学计量点时滴定反应的条件稳定常数为：

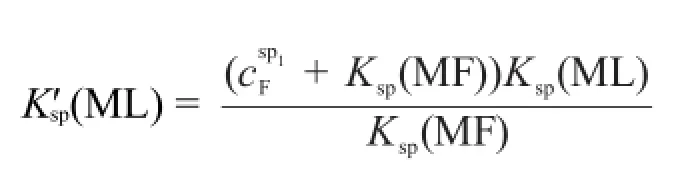
1.2滴定突跃的绝对值

在沉淀滴定中，M滴定L溶液，要求准确度为TE% ≤||±0.1%［1－3］，如果以滴定分数a为横坐标，被滴定离子浓度的负对数pL为纵坐标，则滴定突跃绝对值定义为化学计量点前后0.1%内，滴定突跃在纵坐标方向上的长度。因为沉淀滴定的化学计量点在滴定突跃的中间点，所以用林邦滴定曲线方程计算滴定突跃绝对值是化学计量点的pLsp与化学计量点前0.1%的pLep之差的2倍。即a=1时的pLsp与a=0.999时的pLep之差的2倍。如果用ΔpLt表示滴定突跃绝对值，则：

由文献［1］可知，M滴定L溶液的林邦滴定曲线方程为：

当a=0.999时，a－1=－0.001=－10－3，所以林邦滴定曲线方程变为：

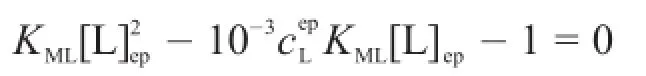
求解并将其两边取负对数得：

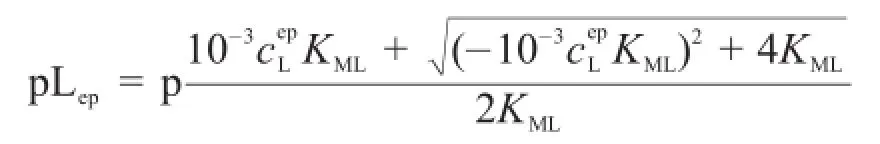
将pLsp和pLep代入式（3）整理得：

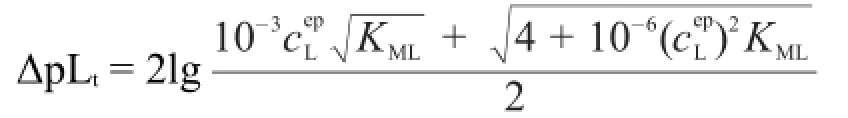
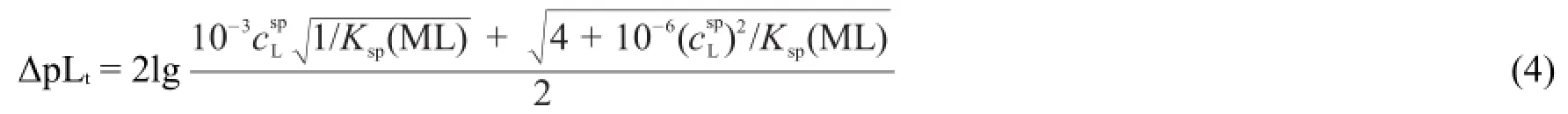
同理，用M滴定混合阴离子（L和F）溶液。假设只有M与F发生副反应，当第一终点要求的准确度为TE% ≤||±0.3%［1－3］时，即a分别为1和0.997（a－1=10－2.5）时，只要用10－2.5和10－5分别替换式（4）中的10－3和10－6，用Kʹsp（ML）替换Ksp（ML）就得到M滴定混合阴离子（L和F）溶液第一滴定突跃绝对值，即：

第一化学计量点后是M滴定F的单一离子滴定，要求准确度为TE%≤||±0.1%，所以第二滴定突跃绝对值与式（4）相同，即：

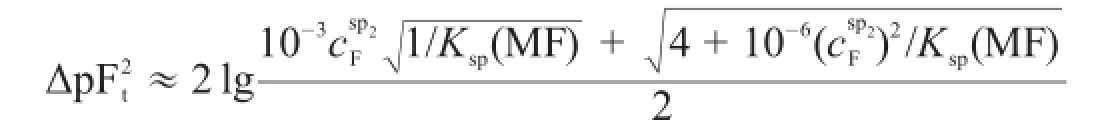
2　混合离子的准确滴定

2.1影响滴定突跃的因素

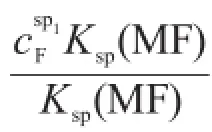
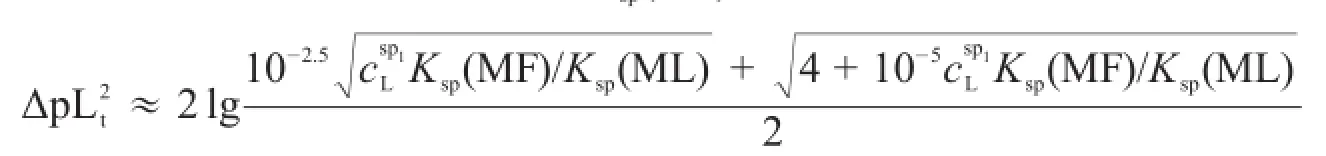
可见，第一滴定突跃绝对值是由csp1K（MF）/K（ML）决定的，csp1K（MF）/K（ML）越大，第一滴定突跃

LspspLspsp绝对值越大，反之越小。

第二滴定突跃绝对值为：

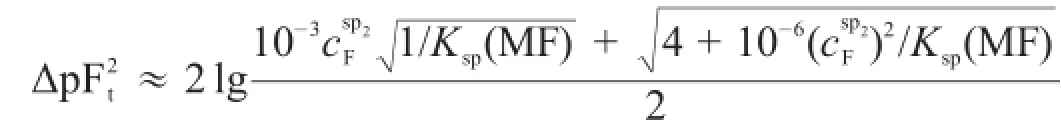
可见，第二滴定突跃绝对值是由csp2和K（MF）决定的，csp2越大，K（MF）越小，第二滴定突跃绝对值越大，反之越小。

如果滴定体系中还有离子强度效应、酸效应和配位效应等副反应发生，在忽略滴定产物发生副反应的前提下，则离子强度效应、酸效应和配位效应越大，第一和第二滴定突跃绝对值就越小，反之越大。

2.2混合离子的准确滴定

2.2.1F离子的准确滴定

因为Ksp（MF）＞Ksp（ML），所以只要F离子能准确滴定，L离子就能准确滴定，也就能够滴定总量。因为第一化学计量点后，L已经反应完，溶液中只有F离子，所以第一化学计量点后是单一离子的滴定。第二终点时，要求ΔpL2=±0.2，TE2%≤||±0.1%［1－3］，而第二滴定突跃绝对值就是在TE2%≤||±0.1%的条件下推导出来的，所以若准确滴定F离子，只要第二滴定突跃绝对值ΔpF2t≥0.4即可：

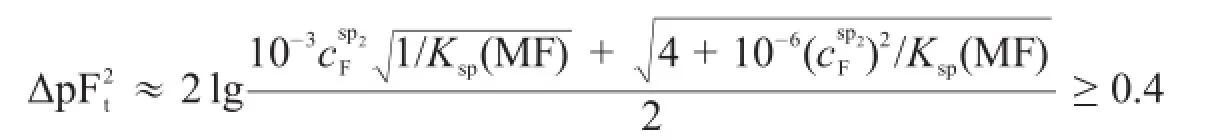
整理得，F离子准确滴定的条件为：

2.2.2L离子的准确滴定

在沉淀滴定中，因为混合离子的准确滴定要求ΔpL1=±0.2，TE1% ≤||±0.3%［1－3］，而第一滴定突跃绝对值就是在TE1%≤|±0.3% |的条件下推导出来的，所以若准确滴定L离子，只要第一滴定突跃绝对值即可：

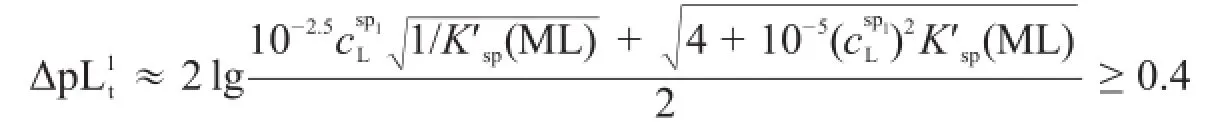
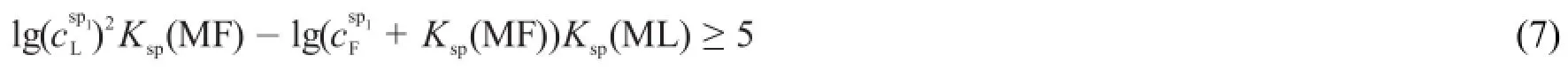
2.2.3L离子准确滴定条件的几何意义

L离子准确滴定条件的最简式为：

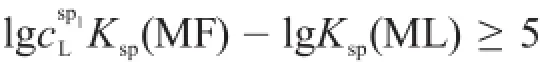
以滴定分数a为横坐标，pL和pF为纵坐标，则csp1K（MF）越小，csp1K（MF）/K（ML）越小，F和 M反应的量越大，第一滴定突跃越向a轴倾斜，使得第一滴定突跃越小。csLp1Ksp（MF）/Ksp（ML）越大，F 和M反应的量越小，第一滴定突跃越垂直于a轴，使得第一滴定突跃越大，所以csLp1Ksp（MF）/Ksp（ML）可以理解为第一滴定突跃的斜率。

3结论

用M滴定混合阴离子（L和F）溶液，Ksp（MF）＞Ksp（ML）。假设只有M与F发生副反应时，F离子准确滴定条件的最简式为：

L离子准确滴定条件的最简式为：

参考文献

［1］武汉大学.分析化学.第5版.北京:高等教育出版社，2006:270－275.

［2］薛华，李隆第，郁鉴源，陈德朴.分析化学.第2版.北京:清华大学出版社，2002:152－155.

［3］彭崇慧，冯建章，张锡瑜，李克安，赵凤林.分析化学.第3版.北京:北京大学出版社，1997:251－257.

中图分类号：O6；G64

doi:10.3866/PKU.DXHX201504029

*通讯作者，Email:qiaocl123@163.com素，并推导出Cl－和I－准确滴定的条件为：

Precipitation Titration for Multiple Ions

QIAO Cheng-Li*
（School of Applied Technology，Qiqihar University，Qiqihar 161006，Heilongjiang Province，P.R.China）

Abstract:The absolute value of titration break in precipitation titration is deduced with the Ringbom titration curve equation，and the conditions for accurate precipitation titration are thus deduced with the absolute value of the titration break.

Key Words:Precipitation titration；Absolute value of titration break；Titration for multiple ions