基于贝叶斯的滑坡稳定性预测对比分析研究*

胡安龙，王孔伟，邓华锋，常德龙，李春波，郭　振，杜常见

(三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002)



基于贝叶斯的滑坡稳定性预测对比分析研究*

胡安龙，王孔伟，邓华锋，常德龙，李春波，郭振，杜常见

(三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002)

摘要:滑坡稳定性的分析是一个复杂的系统工程，影响滑坡稳定性的因素较多。首先，基于相关系数理论描述滑坡稳定性影响因素对滑坡稳定状态影响的大小。再根据关联度大小筛选出影响滑坡稳定性的主要影响因素。其次，引入贝叶斯理论，滑坡稳定性的主要影响因素和滑坡的稳定状态建立了基于贝叶斯的滑坡稳定性预测模型。最后，在贝叶斯理论分析和MATLAB软件的基础上，以竹溪县197组滑坡数据中的100组滑坡数据作为训练样本，其余97组滑坡数据作为测试样本，代入模型进行判别。研究结果表明：其训练集稳定性预测的正确率为80%，测试集稳定性预测的正确率为80.41%。故基于贝叶斯的滑坡稳定性预测模型对于滑坡稳定性分析具有一定参考价值。同时，相关的方法也可以为其他工程研究提供参考。

关键词:滑坡；稳定性;相关系数;贝叶斯理论 ;滑坡稳定性预测模型

滑坡是一种地质灾害，其稳定性是很重要的工程问题。滑坡稳定性主要受地形、岩性、地质构造等多种因素的影响。如何通过滑坡的影响因素快速预测滑坡稳定性的非线性问题是当今滑坡研究的重要工程问题。近年来，模糊综合评价模型，神经网络模型，贝叶斯判别模型和SVM支持向量机模型，取得了较好的预测效果。蔡长发等[1]利用模糊综合评价模型对北川小河进行评价。并通过对比刚体极限平衡法结果，验证了模糊综合评价模型的合理性与稳定性。汪华斌等[2]以边坡高度、内摩擦角等5个因子作为输入模式变量，建立BP人工神经网络模型对滑坡稳定性评价，结果表明鱼洞河滑坡处于不稳定状态。叶四桥等[3]运用改进的BP-NN，构建了三峡库区滑坡稳定性分析的神经网络方法，并选择30个三峡库区典型滑坡作为样本及算例，结果同传递系数法对比后表明，本方法具有较好的可靠性。宫清华等[4]利用人工神经元网络BP模型对国道G324上的86个滑坡稳定性的评价进行预测，结果表明所建立的滑坡稳定性预测方法有较高的预测精度。谢全敏等[5]提出了基于神经网络的岩体边坡稳定性的灰色聚类空间预测方法，结合实列仿真分析，表明该方法可以较好地处理岩体边坡稳定性与影响因素之间的灰色非线性关系。李雪平等[6]利用Logostic回归模型对斜坡稳定性进行评价，滑坡发生样本的判对率72.55%，滑坡不发生样本的判对率为79.69%，故该模型应用于斜坡稳定性评价中具有一定的可行性。马志江等[7]运用支持向量机理论，利用数字高程和遥感数据，构建了滑坡预测的支持向量机模型，并以浙江庆元地区为例，结果表明支持向量机模型可以准确实现滑坡灾害的预测。罗战友等[8]根据影响边坡稳定性的主要因素，建立了边坡稳定性的支持向量机预测模型，结果表明基于神经网络及径向基函数核的分类器能正确判定边坡稳定性。马文涛等[9]提出了粒子群算法和最小二乘法支持向量机的边坡稳定性评价，结果表明，该方法是合理有效的。李秀珍等[10]利用多分类支持向量机模型对滑坡稳定性进行判识，测试样本和训练样本准确率分别为80%和77.8%，结果与实际情况吻合较好。彭令,牛瑞卿等[11-14],运用支持向量机理论对滑坡易发性评价、滑坡地下水位动态预测、滑坡位移预测等三个方面进行了研究，结果表明支持向量机对于解决工程非线性问题十分有效。史秀志等[15]利用贝叶斯模型对边坡稳定性进行预测，研究表明贝叶斯分类性良好，与支持向量机模型有较好的一致性，预测精度高。

表1　竹溪县滑坡详细调查资料

本文拟在阐述相关系数、贝叶斯理论的基础上，建立了基于贝叶斯的滑坡稳定性预测模型，并对竹溪县197滑坡稳定性进行预测，实例结果表明基于贝叶斯的滑坡稳定性预测模型判别的正确率均大于等于80%，故基于贝叶斯的滑坡稳定性预测模型具有一定可行性和工程实际参考价值。

1竹溪县滑坡稳定性主要影响因素的筛选

1.1竹溪县滑坡资料的来源和收集

本文所用的197个滑坡资料来源于湖北省地质环境总站、武汉地质工程勘察院、宜昌长江地质灾害防治工程勘察设计院承担的十堰市地质灾害详细调查项目中的竹溪县地质灾害详查项目。宜昌长江地质灾害防治工程勘察设计院接受十堰国土资源局委托，组成精干项目组。在充分收集已有资料的基础上，于2014年9月16日开始野外工作，野外工作共计两个阶段：第一阶段是9月16日-11月19日，完成1∶5万地质灾害测量(正测)、1∶5万地质灾害测量(草测)的任务，面积3 310 km2；第二阶段是2015年1月9日-2015年2月9日，完成重点地段1∶1万地质灾害测量(草测)任务，面积95 km2。涉及15个乡镇、302个村、4个社区、15个林场和十八里长峡国家级保护区管理局。2015年7月项目完成结题验收。本文所用的竹溪县滑坡资料部分数据如表1所示。

1.2滑坡稳定性影响因素量化与归一化

根据所收集197个滑坡资料分析，发现影响滑坡稳定性的因素众多，为了确定影响滑坡稳定性的主要因素，本文首先对滑坡地层岩性、原始坡型、目前稳定状态、今后变化趋势进行量化处理。

(1)地层岩性量化

利用水利工程中岩石软硬分类表对地层岩性进行软硬分类，再利用软硬岩石所对应的单轴饱和抗压强度对地层岩性进行量化。即分别用单轴饱和抗压强度80 MPa,50 MPa,30 MPa量化硬质岩石、中硬岩石、软质岩石。

(2)原始坡型量化

本文对原始坡型量化，即分别用数值10、30、50、70对坡面形态凸形、直线形、凹形、阶梯型进行量化。

(3)目前稳定状态量化

本文对滑坡目前稳定状态量化，即分别用0,1对滑坡稳定状态较稳定、不稳定进行量化。

为了研究滑坡影响因子与滑坡目前稳定状态和今后变化趋势的相关性，首先消除量纲影响，故本文对滑坡稳定性影响因素和稳定状态的进行了如下归一化处理：

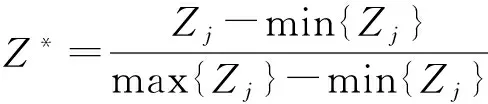
(1)

式中:Z代表滑坡稳定性影响因素和滑坡稳定状态变化值。

1.3滑坡稳定性影响因素和稳定状态相关系数模型建立及求解

衡量两个变量之间的相关性利用相关系数，其价值在于定量刻画两个数据向量的相似程度。

X=(x1,x2,…,xn)T，Y=(y1,y2,…,yn)T。

(2)

对两个变量X与Y之间线性相关程度的度量称为相关系数，相关系数|r|越趋于1表示关系越密切；|r|越趋于0表示关系越不密切。

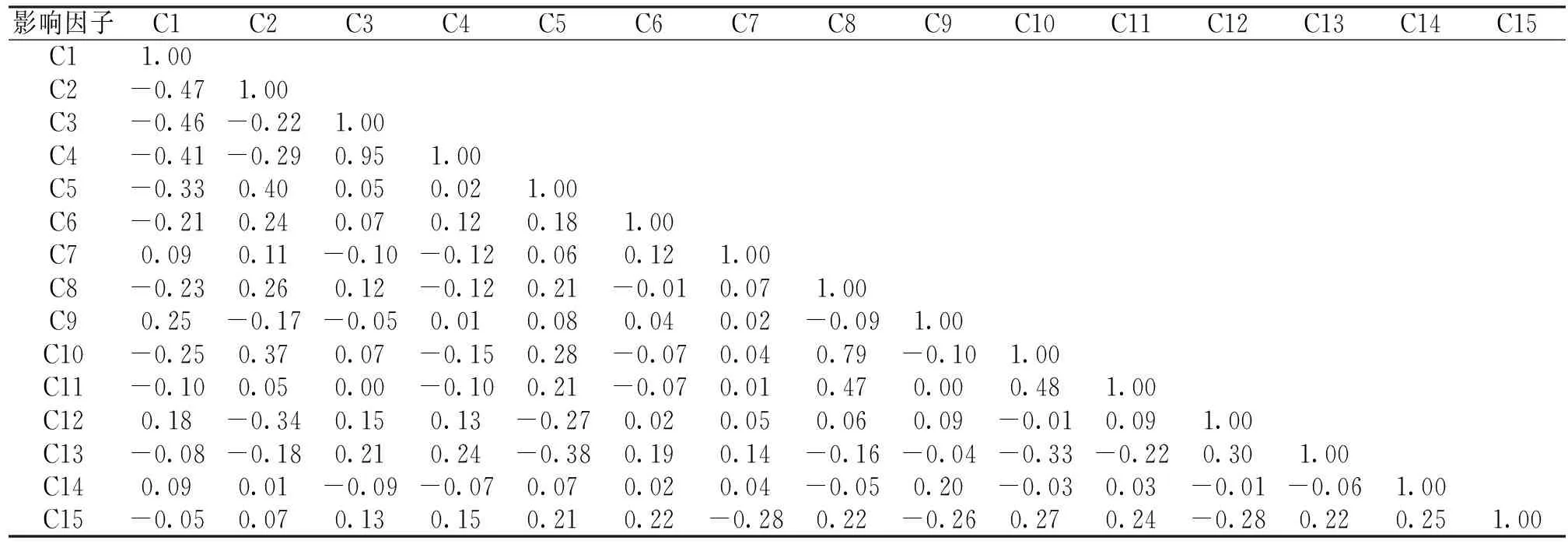
表2　相关系数

数据归一化处理后，本文对滑坡稳定性影响因素和滑坡稳定状态进行相关系数分析，即建立相关系数模型：

(3)

式中:xij表示第j个滑坡中第i个影响滑坡稳定性因素的量化值；yj第j个滑坡的目前稳定状态。

利用MATLAB编程，把经过量化和归一化的197个竹溪县滑坡数据代入式(3)，求解出滑坡稳定性影响因素：滑坡X坐标C1、滑坡Y坐标C2、坡顶高程C3、坡脚高程C4、地层岩性C5、地层倾向C6、地层倾角C7、原始坡高C8、原始坡形C9、滑坡长度C10、滑坡宽度C11、滑坡厚度C12、滑坡坡度C13、滑坡坡向C14与滑坡的目前稳定状态C15相关系数如表2所示。

由表2可知:地层岩性C5、地层倾向C6、地层倾角C7、原始坡高C8、原始坡形C9、滑坡长度C10、滑坡宽度C11、滑坡厚度C12、滑坡坡度C13、滑坡坡向C14与滑坡的目前稳定状态C15的相关系数绝对值均大于0.2，由相关系数可知此其中上述11个滑坡稳定性影响因子与滑坡稳定性具有一定的相关性。坡顶高程C3、坡脚高程C4与滑坡的目前稳定状态C15的相关系数绝对值均小于0.2，由相关系数可知此其中上述2个滑坡稳定性影响因子与滑坡稳定性相关性不大。故选取地层岩性C5、地层倾向C6、地层倾角C7、原始坡高C8、原始坡形C9、滑坡长度C10、滑坡宽度C11、滑坡厚度C12、滑坡坡度C13、滑坡坡向C14等10个影响因子为滑坡稳定性的主要影响因子。

2朴素贝叶斯滑坡稳定性预测模型的建立

2.1朴素贝叶斯理论分析和计算

2.1.2朴素贝叶斯法判别准则

贝叶斯判别是用先验概率来描述人们对研究对象已经有一定的认识。然后通过样本来修正先验概率，得到后验概率。最后基于后验概率进行判别。设有2个p维正态总体G1，G2，概率密度函数分别为f1(x)，f2(x)。假设滑坡样本x来自总体Gi的先验概率为pi(i=1,2)，则有p1+p2=1，根据贝叶斯理论，滑坡样本x来自总体Gi的后验概率为：

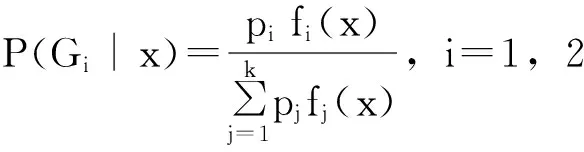
(4)

(1)不考虑误判代价的情况下，有以下判别规则：

(5)

(2)若考虑误判代价的情况下，有以下判别规则。

用Ri表示根据某种判别规则可能判归Gi(i=1,2)的全体样品的集合，用c(i|j)(i,j=1,2)表示将来自Gi的样品x误判为Gj的代价，则有c(i|j)=0。将来自Gi的样品误判为Gj的条件概率为：

P(j|i)=P(x∈Ri|x∈Gi)=∫Rjfi(x)dx

(6)

由式(6)可得任一判别规则的平均误判代价为：

c(j|i)p(j|i)。

(7)

由式(7)，使平均误判代价达到最小的误判规则为：

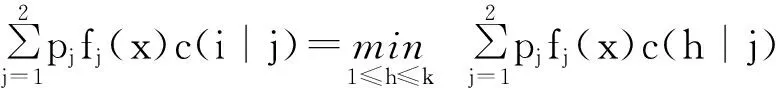
(8)

综上所述，假设样本空间Ω的一个划分:R1和R2=Ω-R1使得平均损失达到极小。故极小化平均损失式(8)的区域为：

(9)

由极小化损失的区域式(9)可知，两总体的贝叶斯判别准则为：

(10)

2.1.3`朴素贝叶斯判别函数

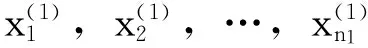
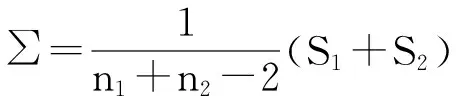
(11)

其中S1，S2为训练样本的的协方差矩阵。且计算公式如下：

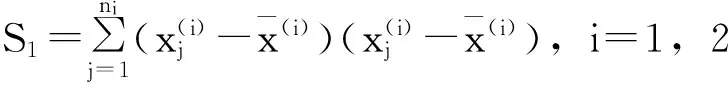
(12)

假定先验概率按训练样本的比列分配，即先验概率为：

(13)

将上述的两总体贝叶斯判别应用于正态分布总体xi～Np(μi,∑i)(i=1,2)，故其概率密度函数为：

(x-ui)}。

(14)

式中:ui为样本均值；∑为协方差。

(1)当∑1=∑2=∑,(∑>0)其中∑>0, 由式(10)～(14)得平均误判损失极小的划分，即判别准则：

(15)

其中w(x)为判别函数，β为判别界限：

(16)

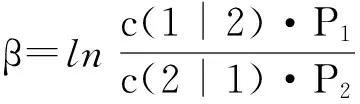
(17)

(2)当∑1≠∑2(∑1>0,∑2>0)，由式(10)～(14)得平均误判损失极小的划分，由于误判损失极小化的划分依赖于密度函数之比f1(x)/f2(x)或等价于它的对数ln(f1(x)/f2(x))，把协方差不等的两元正态密度代入这个之比后，包含|∑i|1/2,i=1,2的因子不能消去,而且fi(x)的指数部分也不能组合简单表达式，因此对于∑1≠∑2时,可得判别区域,即判别准则：

(18)

其中w(x)为判别函数，K为判别界限

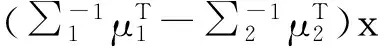
(19)

(20)

2.2基于贝叶斯理论的滑坡稳定状态分析和预测

2.2.1判别因子的确定

判别因子即滑坡稳定性的主要影响因素，由前文中的竹溪县滑坡稳定性主要影响因素的研究结果可知，地层岩性C5、地层倾向C6、地层倾角C7、原始坡高C8、原始坡形C9、滑坡长度C10、滑坡宽度C11、滑坡厚度C12、滑坡坡度C13、滑坡坡向C14等10个影响因子为滑坡稳定性的主要影响因子，故本文以这10个滑坡稳定

性主要影响因子作为贝叶斯模型的判别因子，将滑坡分为较稳定(0)和不稳定(1)，建立贝叶斯判别模型。

2.2.2基于贝叶斯理论滑坡稳定状态预测模型的建立

以前文中所采集的竹溪县197组滑坡实测数据为例(原始数据见表1)，选取其中100个滑坡样本数据进行训练，其余97组滑坡样本数据进行检验。因为滑坡类型分为两类，则中间层为2个对应的判别函数，输出层为G1，G2。并且先验概率按比例分配，即p1=0.75，p2=0.25。假设2个总体协方差相等，即。根据前文中的贝叶斯理论进行计算，再利用MATLAB[14-16]中的朴素贝叶斯分类器对未知类别的样品分类进行求解，得出训练集滑坡稳定性贝叶斯判别结果如表3和图1所示。

图1　训练集滑坡稳定性真实类别和贝叶斯模型判别结果

2.2.3竹溪县滑坡稳定性预测

对比分析100个滑坡训练样本真实稳定性和贝叶斯判别的稳定性，可得贝叶斯判别正确有 80个，误判滑坡稳定性的有20个。故贝叶斯模型的判别准确率为80%。发生误判的可能原因是：滑坡数据采集过程中存在误差，另外选取影响滑坡稳定性的因子还存在不完善之处，训练样本的代表性以及容量的范围还需进一步优化和改善。

由于贝叶斯模型的判别准确率大于等于80% ，即认为所建立的函数模型可投入使用。根据学习好的贝叶斯判别分析模型对97个待判样本进行判别，贝叶斯模型预测判别的结果如表4和图2所示。

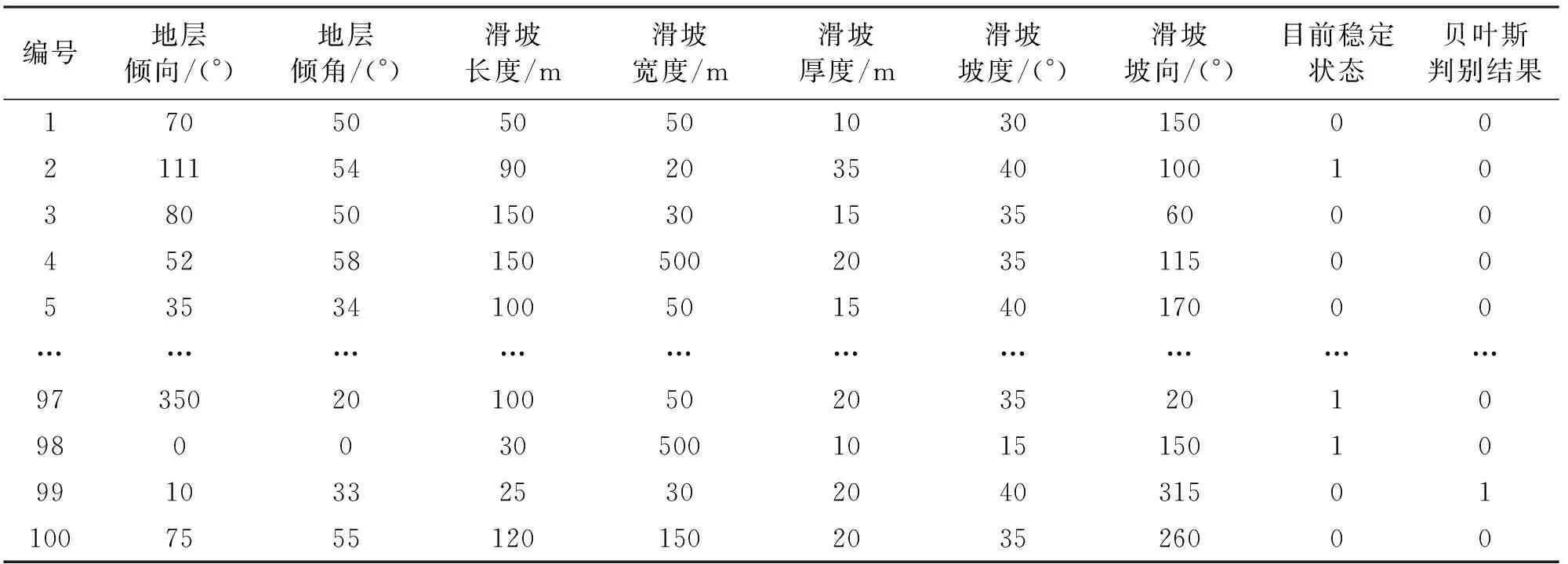
表3　训练集滑坡稳定性真实类别和贝叶斯模型判别结果

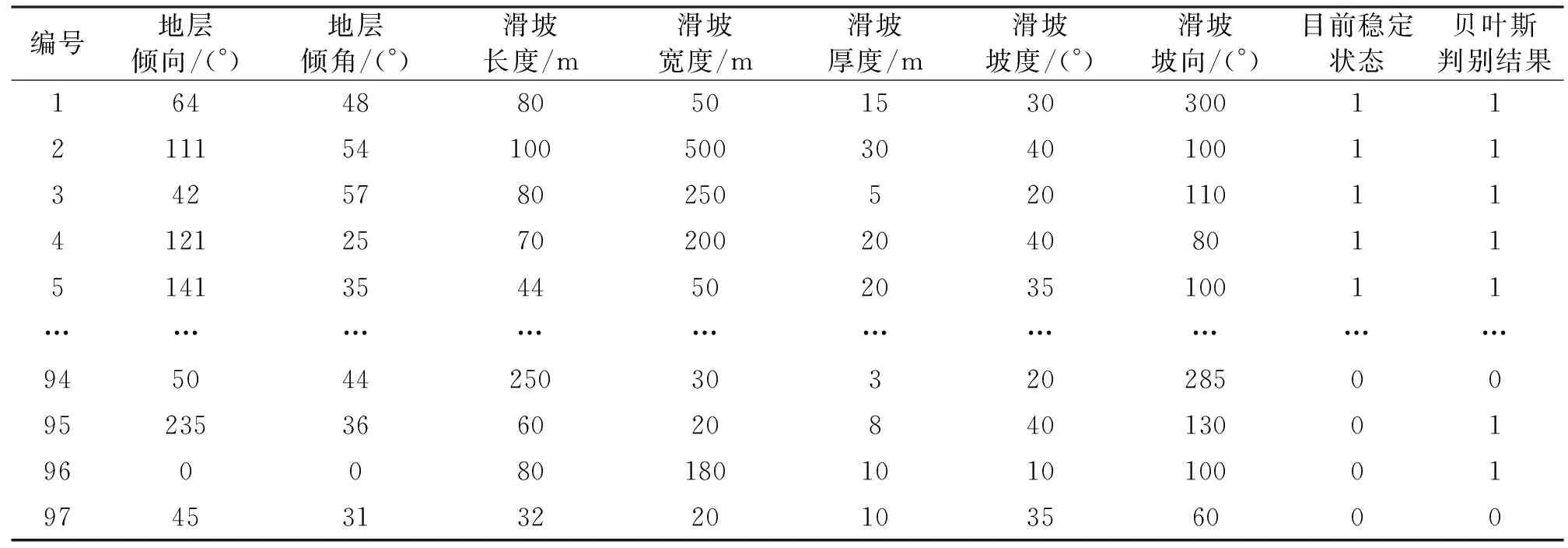
表4　测试集滑坡稳定性真实类别和贝叶斯模型判别结果

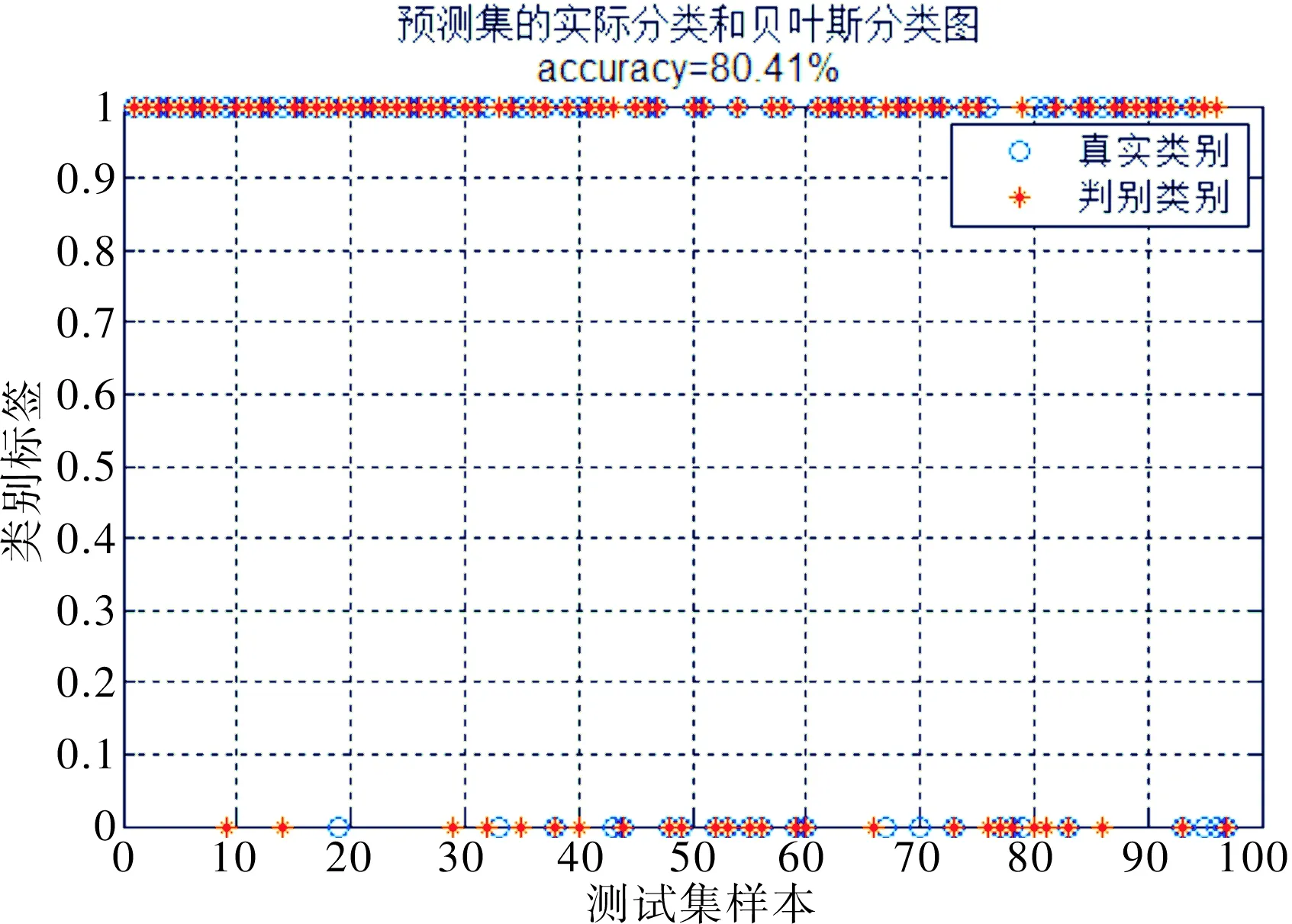
图2　测试集滑坡稳定性真实类别和贝叶斯模型判别结果

对比分析97个滑坡测试样本真实稳定性和贝叶斯判别的稳定性，可得贝叶斯判别正确有 78个，误判滑坡稳定性的有19个。故贝叶斯模型的判别准确率为80.41%。训练集滑坡稳定性预测准确率为84%，均大于80%。故运用贝叶斯理论建立滑坡稳定性判别模型对实际工程滑坡稳定状态进行初步预测具有一定的可行性。

3结论

(1)结合197个滑坡资料和相关系数理论，本文确定出滑坡稳定性的主要影响因素为地层岩性、地层倾向、地层倾角、原始坡高、原始坡形、滑坡长度、滑坡宽度、滑坡厚度、滑坡坡度、滑坡坡向。此方法确定的滑坡主要影响因素符合实际情况。

(2)利用相关系数模型筛选出滑坡稳定性主要影响因素，建立基于贝叶斯滑坡稳定性预测模型，对滑坡稳定性进行预测，其预测结果与实际情况吻合较好，其训练集稳定性预测的正确率为80%，测试集稳定性预测的正确率为80.41%。证明基于贝叶斯滑坡稳定性预测模型具有较强的预测能力。在滑坡稳定性预测方面能为实际工程活动提供一定的参考意义。

参考文献:

[1]蔡长发,陈廷芳,王欢.滑坡稳定性模糊评价方法及其应用[J].西南科技大学学报，2011,26(3)：45-47,52.

[2]汪华斌,徐瑞春.BP神经网络在鱼洞河滑坡稳定性评价中的应用[J].长江科学院院报，2002,19(4)：62-64.

[3]叶四桥,唐红梅,石晋旭.改进BP-NN在三峡库区滑坡稳定性分析中的应用[J].重庆建筑大学学报，2006,28(6)：38-41,83.

[4]宫清华,黄光庆.基于人工神经元网络的滑坡稳定性预测评价[J].灾害学，2009,24(3)：61-66.

[5]谢全敏,夏元友,朱瑞赓.基于神经网络的岩体边坡稳定性的灰色聚类空间预测方法及其应用[J] 灾害学，2001：16(2)：1-6.

[6]李雪平,唐辉明.基于GIS的分组数据Logistic模型在斜坡稳定性评价中的应用[J].吉林大学学报(地球科学版)，2005,35(3):361-365.

[7]马志江,陈汉林,杨树锋.基于支持向量机理论的滑坡灾害预测[J].浙江大学学版(理学版)，2003,30(5):394-399.

[8]罗战友,杨晓军,龚晓南.基于支持向量机的边坡稳定性预测模型[J].岩石力学与工程学报，2005,24(1):144-148.

[9]马文涛.基于PSO和LSSVM的边坡稳定性评价方法[J].岩土力学，2009,30(3):845-848.

[10]李秀珍,孔纪名,王成华.多分类支持向量机在滑坡稳定性识别中的应用[J].吉林大学学报(地球科学版)，2010,40(3):631-637.

[11]牛瑞卿,彭令,叶润青.基于粗糙集的支持向量机滑坡易发性评价[J].吉林大学学报(地球科学版)，2012,42(2):430-439.

[12]牛瑞卿,彭令,叶润青.基于进化支持向量机的滑坡地下水位动态预测[J].中南大学学报(自然科学版)，2012,43(12):4788-4795.

[13]彭令,牛瑞卿,赵艳南.基于核成分分析和粒子群优化支持向量机的滑坡位移预测[J].武汉大学学报(信息科学版)，2013,38(2)：148-152.

[14]赵艳南,牛瑞卿,彭令，等.基于粗糙集和粒子群优化支持向量机的滑坡变形预测[J].中南大学学报(自然科学版)，2015,46(6):2324-2332.

[15]史秀志,周健,郑伟等.边坡稳定性的Bayes判别分析方法及应用[J].四川大学学报(工程科学版)，2010，42(3):63-68.

*收稿日期：2015-11-19修回日期：2016-01-20

基金项目：国家自然科学基金资助项目(51309141)；水利部公益基金项目(201401029)；2015年三峡大学研究生科研创新基金(2015CX036)

第一作者简介：胡安龙(1991-)，男，湖北鄂州人，硕士研究生，研究方向建筑与土木工程. E-mail：807095067@qq.com 通讯作者：王孔伟(1966-)，男，湖北宜昌人，副教授，研究方向地质灾害成因机理. E-mail：807095067@qq.com

中图分类号：X43；P642.22

文献标志码：A

文章编号：1000-811X(2016)03-0202-06

doi:10.3969/j.issn.1000-811X.2016.03.034

Comparative Analysis of Landslide Stability Prediction Based on Bayesian Theory

HU Anlong, WANG Kongwei, DENG Huafeng, CHANG Delong, LI Chunbo,GUO Zhen and DU Changjian

(ChinaThreeGorgesUniversityKeyLaboratoryofGeologicalHazardsonThreeGorgesReservoirArea,MinistryofEducationUniversity,Yichang443002,China)

Abstract:The analysis of landslide stability is a complex systematic project, which affects the stability of landslide. Firstly, based on the correlation coefficient theory, the influence factors of landslide stability are described. According to the correlation degree, the main factors affecting the stability of the landslide are selected. Secondly, based on Bayesian theory, the main factors affecting the stability of the landslide and the stability of the landslide are established. Finally, in Bayesian theory analysis and MATLAB software based, Zhuxi County group of 197 landslide data in the group of 100 landslide data as training samples, the remaining 97 group landslide data as the test sample, is substituted into the model discrimination. The results show that the stability of the training set is 80%, and the stability of the test set is 80.41%. Therefore, Bayesian based landslide stability prediction model has a certain reference value for landslide stability analysis. At the same time, the related method can also provide reference for other engineering research.

Key words:stability of landslide; related coefficient; Bayesian theory; prediction model of landslide stability

胡安龙，王孔伟，邓华锋，等. 基于贝叶斯的滑坡稳定性预测对比分析研究[J].灾害学, 2016,31(3):202-206,210.[ HU Anlong, WANG Kongwei, DENG Huafeng,et al.Comparative Analysis of Landslide Stability Prediction Based on Bayesian Theory[J].Journal of Catastrophology, 2016,31(3)：202-206,210.]