基于地质统计学与Surpac软件的夏甸金矿区矿化空间分析

李　媛，毛先成，潘诗辰，崔振营

(中南大学地球科学与信息物理学院，长沙 410083)



基于地质统计学与Surpac软件的夏甸金矿区矿化空间分析

李媛，毛先成，潘诗辰，崔振营

(中南大学地球科学与信息物理学院，长沙 410083)

摘要：矿区外围及深部的成矿预测需要对老矿区矿化空间分布进行定性分析，提取最有利的矿化指标，为控矿规律分析和成矿区圈定提供技术支持。文章以山东夏甸金矿床Ⅶ号矿体群为例，利用Surpac软件建立该矿区地质数据库，进行实验变异函数的计算与理论变异函数拟合，通过交叉验证，获取最优的搜索椭球体参数，构建搜索椭球体模型，揭示出矿体的矿化分布规律，最后在各三维坐标轴平面绘制矿化投影等值线图，直观地展示矿体内部金品位的连续方向，为矿化指标计算提供数据支撑。

关键词：夏甸金矿床；地质统计学；变异函数；矿化空间分析；山东省

0引言

胶东金矿集中区是我国最重要的黄金生产基地，持续不断地开采使矿山面临资源危机，开展矿区外围及深部隐状矿预测以实现资源的延续极为迫切[1-2]。隐伏矿体立体定量预测需要预先利用地质统计学等方法对矿体的品位、金属量等进行估算，以便获得隐伏矿体定量预测建模的重要指标——矿化指标[3]。

地质统计学是在矿山储量计算工作中发展起来的，法国地质统计学家G.Matheron经过研究提出的以变差函数为工具，以区域化变量理论为基础，研究在空间分布上既有结构性又有随机性自然现象的一个数学地质学科分支[4]。克里格方法是地质统计学的重要组成部分，是以南非矿业工程师D.G.Krige命名的一项实用空间估计技术[5]。矿化空间分析简单来说，就是利用地质统计学的结构分析方法，构建具有矿体标志的变异函数模型，研究矿体内部的空间变化结构性特征[6]。对于变异函数模型参数的求解即对变异函数模型的拟合，实际上是非线性优化问题，通过求得一组参数值(基台值、块金值、变程)，使得实验变异函数值与理论变异函数值最接近，建立变异函数椭球体的三维模型。然后通过交叉验证，检验变异函数模型的可靠性，对满足要求的结构参数，利用克里格方法对区域化变量金品位进行估值，生成区内矿体区域化变量矿化投影等值线图，为深边部隐伏矿体预测提供参考。

图1　夏甸金矿区招平主裂面三维线框模型Fig.1　3D solid model of Zhaoping fault surfaceVulcan视角：方位角4°，倾角-26°

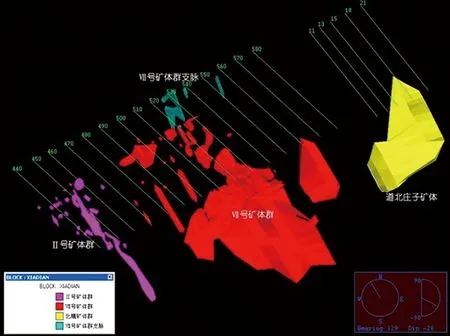
图2　夏甸金矿区矿体群三维线框模型Fig.2　3D solid model of ore bodies in Xiadian depositVulcan视角：方位角345°，倾角-15°

1矿体地质特征

运用Vulcan三维建模软件对矿区内断层(图1)和矿体(图2)进行三维可视化模拟和表达，可以看出，夏甸金矿床Ⅶ号矿体群位于招平断裂带的中段，断裂带主裂面上盘蚀变较弱，下盘蚀变较强，总体走向45°～50°，倾向SE，倾角34°～50°。夏甸金矿区矿体群赋存于主裂面下盘几米至几十米内，走向长450 m，倾向SE，倾角较稳定，约48°，多数矿体大致与主裂面平行。Ⅶ号矿体群为夏甸矿区的主要矿体群，主要分布于485—565线；Ⅱ号矿体群分布于Ⅶ号矿体群西南方440—475线，倾向SE，倾角42°～50°，走向方向矿化连续性较弱，倾向方向矿化较稳定；道北庄子矿体分布于夏甸金矿区东北端，倾向SE，倾角较稳定，厚度方向、走向以及倾向矿化都较稳定。夏甸金矿区矿体群的矿体厚度、品位沿走向变化不明显，但随深度的增加矿体厚度呈逐渐增大的趋势，而品位逐渐降低。

2实验过程

矿体各种标志(矿石品位、矿体厚度等)在空间上的变化既具结构性又有随机性[7-8]。矿化空间分析前，需收集原始数据、数字化地质资料，创建地质数据库，建立区内矿体三维线框模型；在此基础上，利用地质统计学的结构分析方法和Surpac软件构建具有矿体标志的变异函数模型，研究矿体空间变化的结构性特征；再利用普通克里格插值进行区域化变量估值，在三维软件Surpac中显示插值后矿体块体模型，生成矿区内矿体平均品位矿化投影等值线图，为深边部隐伏矿体预测提供参考。矿化结构分析过程见图3。

2.1数据预处理

本次实验所需的原始数据有钻孔柱状图、地质剖面图、勘探线剖面图和中段平面图。通过数字化，将上述地质资料按照Surpac软件中数据表结构的要求整理出3类数据表：化验数据表(sample表)，测斜数据表(survey表)和开孔数据表(collar表)。各表之间通过钻孔号进行关联[9]。各数据表结构见表1。在Surpac中创建地质数据库，导入适合该软件接收的.txt或.csv文件格式数据表，在数据库中可对原始数据进行编辑、查询、统计分析等。

为保证统计参数是无偏估计量，地质统计学要求参与统计的样品数据均应具有相同的支架或承载，在计算金属量和品位前，一般需对取样数据进行预处理，包括样品组合处理和特高品位样品的处理[10]。因此，需对夏甸金矿床矿体群所有钻孔中的样品进行组合，形成长度相等的组合样品。组合样样长的选取应以最少拆分原始取样长度为原则，根据不同矿区取样长度的分布规律进行组合。Surpac软件可对区内各矿体群样品数据(样品数量、长度、最大长度、最小长度、均值、标准差和方差等)进行基本统计。经计算，得到平均样长为1.05 m的组合样品数据共32 730个(表2)。

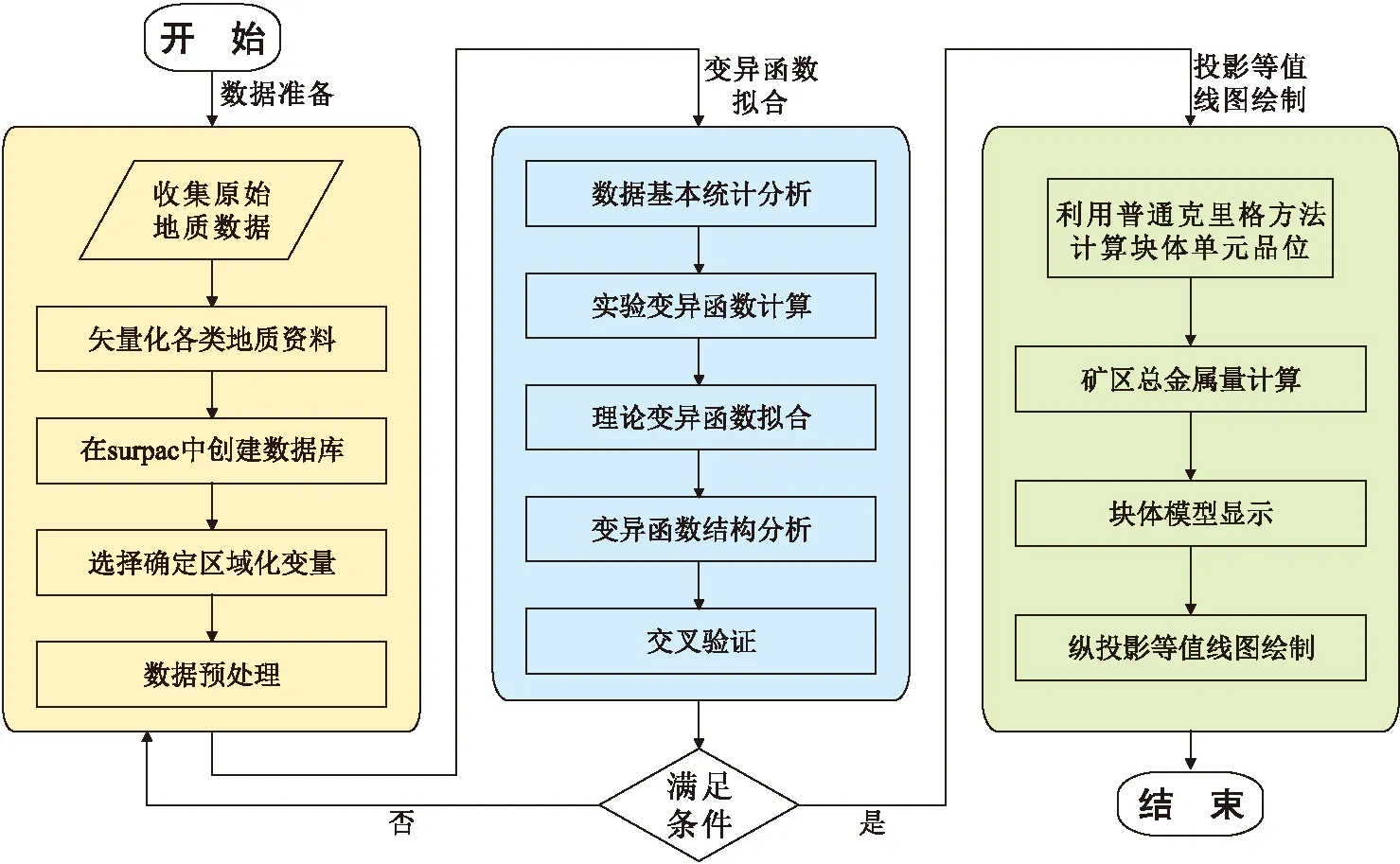
图3　矿化结构分析流程图Fig.3　Structural analysis flowchart of mineralization

2.2变异函数拟合

地质统计学通过克里格方法，在原始数据和变异函数结构性的基础上，对有限区域内区域化变量的未知采样点进行最优无偏估值。无偏是指偏差的数学期望为零，最优则是指估计值与实际值之差的平方和最小[11]。变异函数可反映不同方向上金属品位的空间相关性大小，是克里格储量估算的基础。实际矿体各个方向的变化性是各不相同的，需要进行结构套合，用同一个模型来表示矿体品位在整个空间上的变异性。通过该过程能确定估算中所需的各种参数，有利于更准确地估算矿体中的金属量。该金属量是后期深边部成矿预测一个重要的矿化指标。变异函数结构套合的过程可简单理解为用一个三维模型来表示矿体品位在各个方向变化的差异

表2　夏甸Ⅶ号金矿床钻孔样品化验金品位统计

性，在后面的实验中，将在走向、倾向和厚度3个方向对夏甸金矿床样品数据进行变异函数曲线的拟合。

不同的克里格方法有各自适用的条件，在进行克里格插值前需要进行数据分析，对不符合正态分布假设的数据应进行数据变换，转为符合正态分布的形式，并尽量选取可逆的变换形式。常见的品位分布有4种情况：品位变化中等的正态分布，品位变化小的正态分布，对数正态分布，“双态”分布。通过统计夏甸金矿区组合样样品品位，可以看出该矿区品位变化符合对数正态分布，所以采用取对数的方法将样品数据转换为正态分布形式(图4，图5)。

(1)实验变异函数拟合。

进行变异函数拟合首先拟合走向方向的最优实验变异函数，确定块金值和基台值，再对另2个方向上的实验变异函数进行优化拟合，最后得到3个方向上的拟合理论变异函数轴，提取变差图的值，得到样本的结构参数，包括块金值、基台值以及变程。在拟合3个方向的实验变异函数之前，需要确定主要的计算参数，结合夏甸金矿区矿体的产状(走向40°～48°，倾向SE，倾角较稳定，平均45°)，由此输入变差图计算所需各项参数(平面倾角、倾角方向、展开、滞后距等)(表3)。

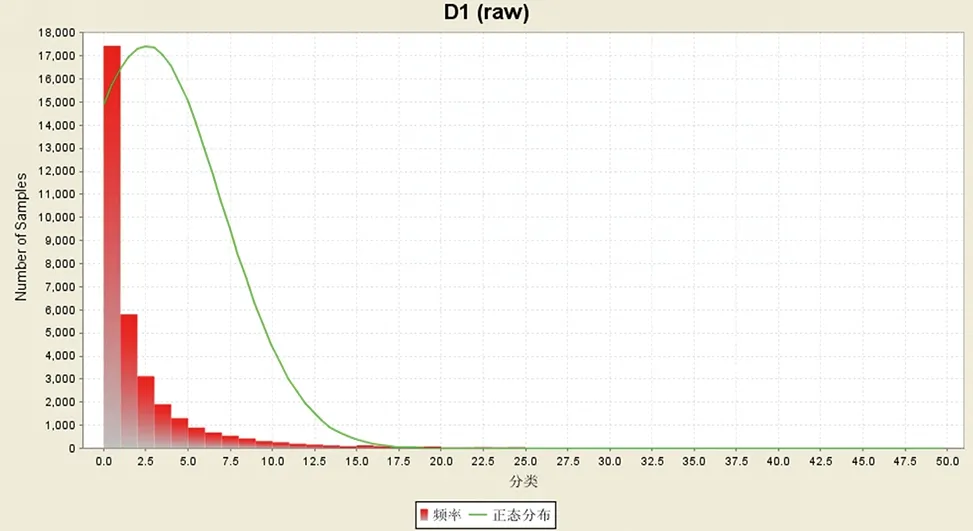
图4　原始样品品位分布直方图Fig.4　Histogram of Au grade of original sample

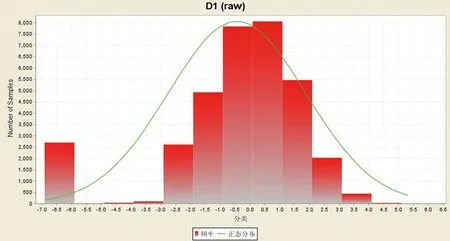
图5　经过对数处理后组合样品品位分布直方图Fig.5　Histogram of Au grade of composite sample after logarithas process

参 数说 明倾角计算变异函数的搜索的中线方向展开角度允许误差限展开极限圆锥到一定的距离,收敛到一个柱体,展开极限为柱体半径滞后又称为步长最大距离滞后距容许误差限,模型为滞后距的一半

利用Surpac软件对变异椭球体3个轴方向的实验半变异函数，采用球状模型进行拟合[12-13]。选择球状模型分别在走向、倾向和厚度3个方向上的最佳拟合结果。图6是选定为主轴方向、次长轴和短轴方向的变异函数曲线和方差图，所确定的理论变异函数的主要参数见表4，表5。

沿轴提取3根轴实验变异函数(图7)后，通过改变“各向异性”获取主轴、次轴及短轴的变程比值，各向异性(anisotropy)代表着属性会随着方向的改变而发生系统性变化的状况[14]，创建椭球体报告将各向异性椭球体参数保存，利用Surpac生成变异函数椭球体(图8)。

从图6和表4、表5大致可看出，矿体矿化主方向的连续性较其他2个方向强，而厚度方向的连续性最弱。换言之，在该矿体内部，在矿体走向上品位

表4　夏甸金矿区样品理论

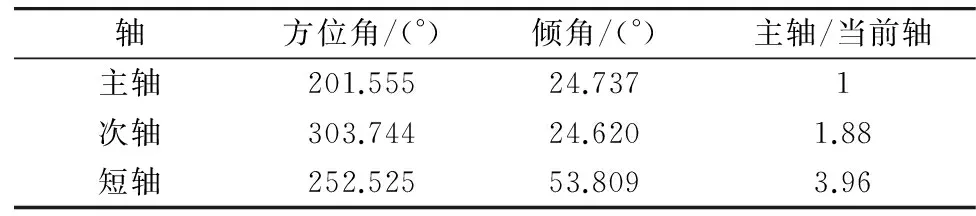
表5　夏甸金矿区样品金品位

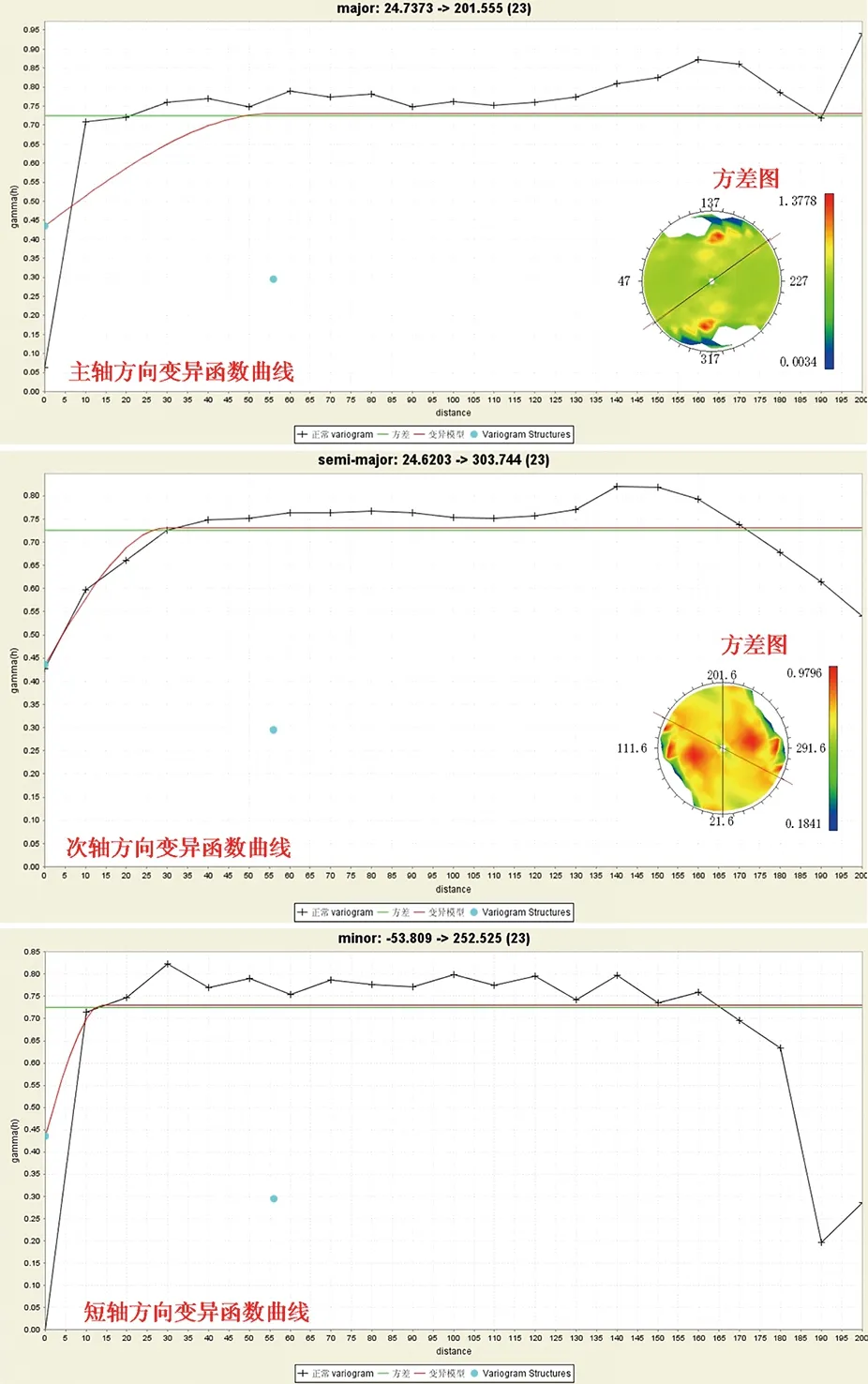
图6　夏甸金矿区主轴、次轴和短轴方向的实验变异函数曲线和方差图Fig.6　Diagram showing experimental variogram and variance of along major semi axis & minor axis for Xiadian mining area

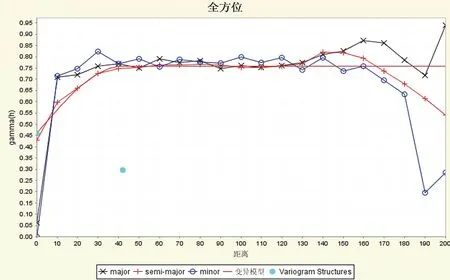
图7　夏甸金矿区全方位实验变异函数曲线图Fig.7　Diagram showing experimental variogram and variance of the all axis for Xiadian mining area

图8　夏甸金矿区变异椭球体Fig.8　Spatial variation ellipsoid of Au grade in Xiadian mining area

变化程度较小，倾向次之，厚度方向上品位变化程度最大。由于计算实验变异函数只是运用变异函数理论或地质统计学方法时的一个开始部分，通常情况下还需对矿体内部的矿化规律进一步深入分析，如进行各平面矿化投影等值线图的绘制和分析。

(2)交叉验证。

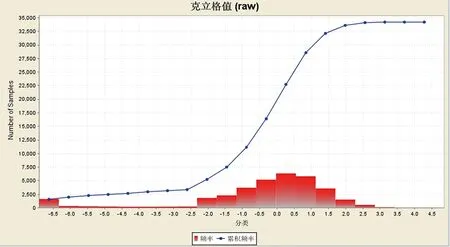
图9　交叉验证克里格方差图Fig.9　Variance map of Cross-validation Kriging

交叉验证的原理是把部分实测点上的观测值与已选出的结构模型计算出的估计值进行比较，如果误差的均值区域为零且方差较小，所得到的结构参数满足要求[15]。对满足要求的参数，进行下一步操作。从图9、表6可知，交叉验证误差均值，误差方差和误差标准差都趋近于零，而标准差范围内误差所占比例都高于95%。表明用该组变异函数曲线参数对组合样品进行估计是无偏的，满足区域化变量的内蕴假设，即验证了该变异函数的模拟是正确的[16]。

表6　各向异性变异函数参数的交叉验证结果

(3)储量估算。

利用Surpac软件将夏甸金矿区矿体的线框模型转换成规格为2 m×2 m×2 m的块体模型，利用距离加权平方反比法和克里格法分别计算矿体单元金平均品位，生成块体模型并按照插值后各块体的金品位进行显示(图10)。根据储量核实报告，夏甸金矿区矿体群矿体的矿石体重为2.86 t/m3，将该值带入公式：2 m单元金属量=平均品位×23×矿石体重，计算块体单元金属量，然后将所有的块体单元金属量累加即可获得夏甸金矿区矿体块体模型总金属量，这与矿区储量核实报告中估算金属量的差值在可控范围之内，再次证明该变异函数的模拟是正确的。

2.3矿化投影等值线图

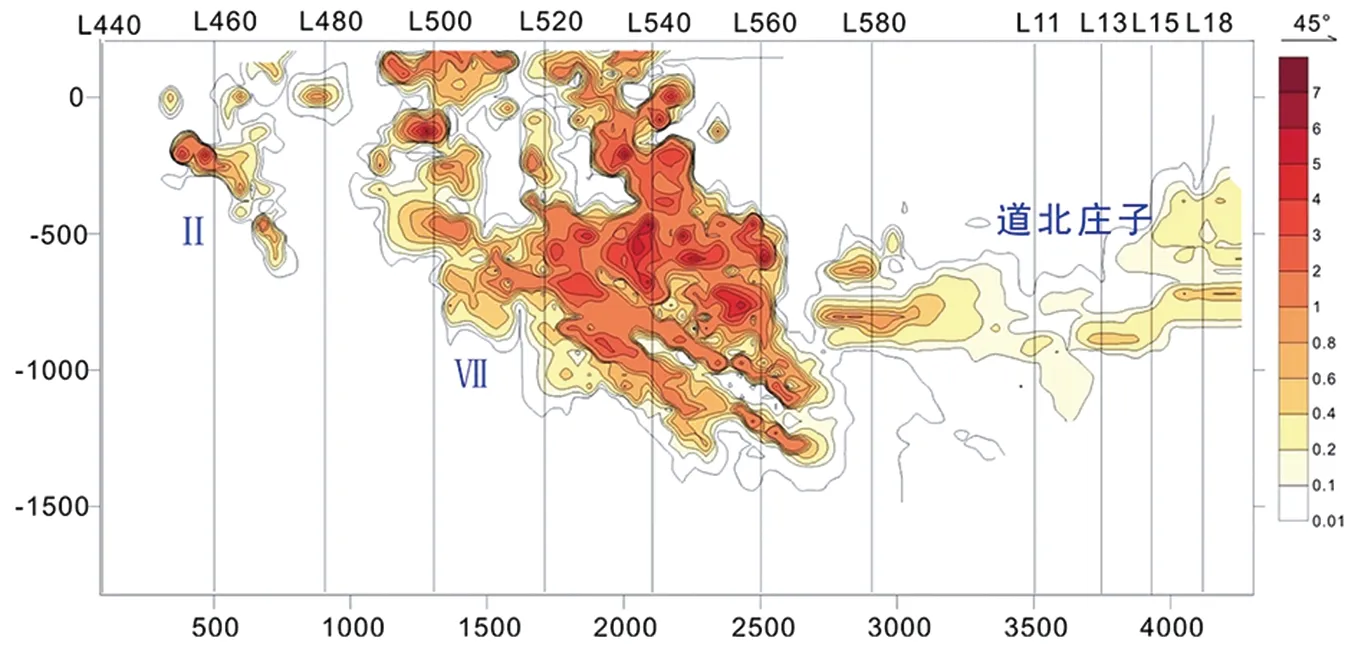
图10　夏甸金矿区Ⅶ号矿体群按品位显示块体模型效果图Fig.10　Block model of Xiadian Ⅶ ore body group by Au grade

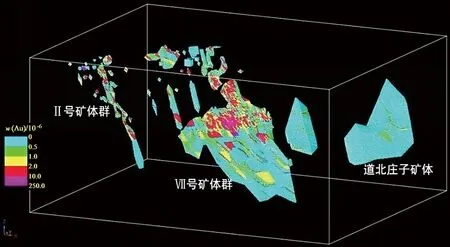
图11　纵投影面金平均品位投影等值线图Fig.11　Contour map of average goldgrade on vertical projection surface

在矿体块体模型插值获得块体单元平均金品位的基础上，确定矿区纵剖面，其上随意取3个点获取纵剖面方程组，求取方程参数，然后将块体单元的坐标通过投影变换映射到该纵剖面上，利用Surfer软件生成夏甸金矿区纵投影平面平均金品位投影等值线图(图11)。纵投影平面即纵剖面视角，从这个角度可观察到矿体群在纵剖面上投影的矿化强度分布。从图11可见，从-1 500 m范围内大致有3条矿化富集带：第一条在-800 m以浅，其品位较均匀，累积金属量也较均匀，靠地表略高一些；第二条从地表到-1 500 m以浅，该带是矿的主体，呈两端较弱、中间较强的大盲矿体形态；第三条在-1 500 m以深，仅显示为矿化，还未出现工业矿体，预示在深部可能会有大隐伏矿体存在。3条带方向一致，均约为40°方向，这与矿体40°左右的侧伏方向相吻合。

3结论

利用地质统计学方法和Surpac软件对区域化变量Au品位进行实验变异函数拟合和克里格插值，用实验变异函数椭球体直观地表现了矿区内矿体3个轴向(走向、倾向、厚度)的空间相关性，可以看出各个轴向金品位的连续性，有利于后期推断深部和外围矿体的延续方向；利用Surpac软件的三维显示功能，将矿区内矿体块体模型按照金品位进行显示，展现了空间范围内矿体品位的分布规律；利用Surfer软件绘制纵投影平面平均品位投影等值线图，将定性分析进行量化，表现了矿区内矿体金品位各方向的变化梯度，为后期隐伏矿体预测提供了数据支撑。

参考文献：

[1]翟裕生，邓军，杨立强，等. 山东夏甸金矿及其外围矿区隐伏矿体定位预测[J]. 地学前缘，1999，6(2)：230-230.

[2]彭省临，邵拥军. 隐伏矿体定位预测研究现状及发展趋势[J]. 大地构造与成矿学，2001，25(3)：329-334.

[3]毛先成，戴塔根，吴湘滨，等. 危机矿山深边部隐伏矿体立体定量预测研究：以广西大厂锡多金属矿床为例[J]. 中国地质，2009，36(2)：424-435.

[4]常维. 地质统计学及其在地质工程中的应用分析[J]，价值工程，2011(29)：81.

[5]Journel A. G.Kriging in terms of Projections[J]. Journal of the lnternational Association for Mathematieal Geology,1977,9(6):563-586.

[6]孙洪泉. 地质统计学及其应用[M]. 徐州：中国矿业大学出版社，1990：1-282.

[7]李岭. 地质统计学及其在某铜矿山储量计算中的应用[J]. 矿业研究与开发，2004，24(5)：21-23.

[8]孙英君，王劲峰，柏延臣. 地统计学方法进展研究[J]. 地球科学进展，2004，19(2)：268-274.

[9]邵毅，马春，毛先成，等. 丁家山铅锌矿床三维可视化预测[M]. 北京：地质出版社，2010：1-243.

[10]万昌林，朱利平，高祥. 应用地质统计学评估福建某铜矿资源[J]. 金属矿山，2002(6) ：49-52.

[11]汤国安，杨昕. ArcGIS地理信息系统空间分析实验教程[M]. 北京：科学出版社，2006.

[12]Johnson T. Structural block modeling at BHP iron ore’s Mt Whaleback Mine[R]. Australian Institute of Mining and Metallurgy,2001,23:169-186.

[13]Neilson L, Kapageridis I. Environment management with Vulcan[CP].Envirosoft, 2000:461-470.

[14]WIKIPEDIA. Isotropy[EB/OL]. http:∥en.wikipedia.org/wiki/I-sotropy.

[15]李晓利，谢玉玲，陈伟. 基于变异函数的三维矿体结构分析及应用[J]. 煤炭技术，2010，29(2)：134-137.

[16]罗周全，王中民，刘晓明，等. 基于地质统计学与Surpac的某铅锌矿床储量计算[J]. 矿业研究与开发，2010，30 (2)：4-6，69.

The spatial analysis of mineralization in Xiadian gold mining area based on Geostatistics and Surpac software

LI Yuan, MAO Xiancheng, PAN Shichen, CUI Zhenying

(SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China)

Abstract：Qualitative analysis of spatial distribution of mineralization in old mining area and extraction of most favorable mineralization index is necessary for the ore prediction to the depth and in the surroundings. The analysis and extraction could provide technical support for analysis of mineralization law and delineate favorable metallogenic spaces of the predicted areas. This paper, taking ore body group Ⅶ in Xiadian gold deposit for example, builds geological database and uses Surpac software to calculate experimental Variograms and fit theoretical Variograms and obtain the best search ellipsoid parameters and build search ellipsoid model which reveals the distribution law of mineralization. Finally, the projection of mineralization contour map is drawn in the three-dimensional coordinate axis plane which intuitively display continuous direction of the gold grade inside ore body and provide a data basis for computing subsequent mineralization indicators.

Key Words：Xiadian gold deposit; geostatistics；variograms；spatial analysis of mineralization；Shandong province

收稿日期：2014-12-12；责任编辑：赵庆

作者简介：李媛(1989—)，女，硕士研究生，研究方向为地学三维建模和隐伏矿立体预测。

通信地址：中南大学校本部地学楼436室；邮政编码：410083；E-mail：liyuanjob@163.com 通信作者：毛先成(1963—)，男，教授，博士，主要从事地学三维建模和隐状矿立体预测研究。 中南大学校本部地学楼420室；邮政编码：410083；E-mail：xcmao@126.com

doi：10. 6053/j. issn.1001-1412. 2016. 01. 003

中图分类号：P628.2

文献标识码：A