高速客车曲线通过性能及稳定性研究

马　彪

(郑州铁路局郑州动车段，河南 郑州　450000)



高速客车曲线通过性能及稳定性研究

马彪

(郑州铁路局郑州动车段，河南 郑州450000)

摘要：针对高速客车曲线通过横向振动数学模型，基于matlab数值仿真对车辆系统稳态曲线通过性能进行研究，采用升速法计算出系统的非线性临界速度，分析系统超过临界速度后蛇行失稳现象及车辆稳态通过曲线时一系、二系悬挂刚度对轮轨横向力、轮对冲角、轮对横移量的影响。结果表明，车辆曲线通过性能主要与一系纵向刚度有关，并且对一系纵向刚度值在相对较小范围内变化比较敏感；当曲线半径为3500 m，外轨超高量为60 mm时，系统非线性临界速度为46.5 m/s，较直线轨道减小，稳定性降低。

关键词：高速客车；曲线通过；蛇行运动；一系悬挂；二系悬挂

车辆稳态曲线通过时，系统横移量受很多因素的影响，如车轮锥度、速度、车辆悬挂参数等。当车辆系统超过非线性临界速度运行时会发生蛇行失稳现象，从而导致轮轨相互作用加剧，轮对及钢轨磨耗严重，恶化列车运行品质，甚至可能引起列车脱轨事故；所以，对列车曲线通过性能及稳定性问题的研究显得十分必要。长期以来，国内外许多学者对车辆系统直线运行分岔及稳定性问题进行了大量的研究，而对曲线通过动力学方面的研究较少。一些学者基于车辆系统多刚体动力学研究了高速客车转向架曲线轨道运行的稳定性问题。

本研究基于车辆-轨道耦合动力学理论，建立高速客车曲线通过横向振动整车数学模型，充分考虑其中的非线性因素，如非线性接触几何关系、非线性蠕滑力、轮缘力等，深入研究系统稳态曲线通过性能，计算得出系统的非线性临界速度及发生蛇行失稳时的极限环、频率和波长，并且得出车辆一系、二系悬挂刚度对轮轨横向力、轮对冲角、轮对横移量的影响，从而为高速客车曲线通过性能及稳定性二者之间的匹配关系、车辆悬挂参数优化设计及制定高速客车曲线通过限速等标准规范提供理论依据。

1曲线轨道高速客车的定常运动

当车辆稳态通过曲线轨道时，由于曲线半径及外轨超高的影响，曲线轨道运行时增加了离心力，且只有一部分离心力被重力平衡，此时系统的平衡位置不再是轨道中心线，而是与中心线偏移一段距离，见图1。

图1　1位轮对时间历程图

以下算式中都取基准参数曲线半径R为3500 m，外轨超高量h为60 mm，Kpy为5×106N/m，Kpx为107N/m，Ksy、Ksx都为1.5×105N/m。

2曲线轨道高速客车的蛇行失稳现象

当车辆运行速度超过非线性临界速度时，系统会发生蛇行失稳现象，具体表现为各刚体由定常运动变为左右振荡的周期运动，其相图为封闭的极限环。

2.1车辆系统非线性临界速度求解

车辆系统在实际运行中，非线性临界速度是保证行车安全以及稳定性分析的重要指标；因此，求出该值尤为必要。本研究采用一种比较简单的方法——升速法求解非线性临界速度，计算结果如图2所示。

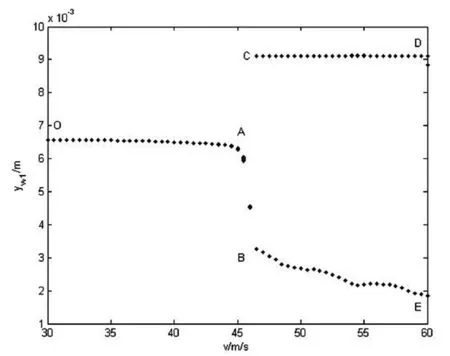
图2　1位轮对最大横向位移分岔图

由图2可知，给一个大的横向扰动(8 mm),速度从30 m/s以定步长0.5 m/s逐渐增大，当速度达到C点46.5 m/s之前，系统都收敛至平衡位置OA段;当速度超过C并继续增大时，系统沿极限环CD和BE做周期运动。因此,46.5 m/s即为系统的非线性临界速度。

2.2系统发生蛇行失稳极限环分析

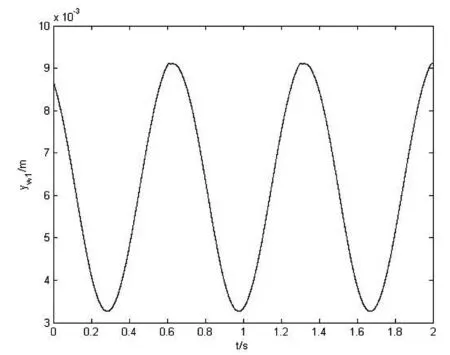
由以上可知：车辆曲线通过非线性临界速度为46.5 m/s，考虑实际运行情况，在此取刚发生蛇行失稳时的速度作为分析对象，并由图3可知，须给一个大的横向扰动，此处给定值8 mm。当系统达到非线性临界速度，轮对就会做周期性的横向振荡运动，且与外轨发生碰撞,见图3。

3车辆系统稳态曲线通过参数研究

评价车辆稳态曲线通过性能主要有轮轨横向力、轮对冲角、轮对横移量三个指标。本文主要研究一系悬挂横向、纵向刚度及二系悬挂横向、纵向刚度对以上三个指标的影响。

(a)

(b)

3.1一系悬挂刚度的影响

两参数分别为一系横、纵向刚度Kpy、Kpx。取基准参数v为40 m/s、Ksx=0.15 MN/m、Ksy=0.15 MN/m，Kpy变化范围为0～15 MN/m,Kpy变化范围取0～10 MN/m，外轨超高h大小为60 mm，曲线轨道半径R为3500 m，其余参数取基准值。

一系悬挂横向、纵向刚度对轮轨横向力、轮对冲角、轮对横移量的影响见图4、图5、图6、图7。

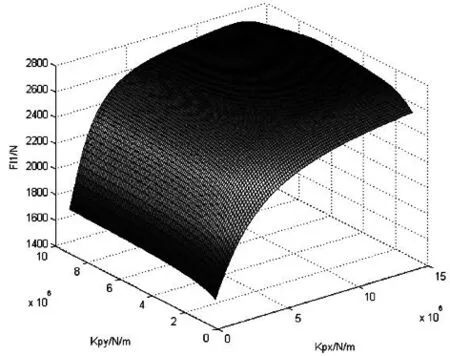
(a)1位轮对左侧　　　　(b)1位轮对右侧

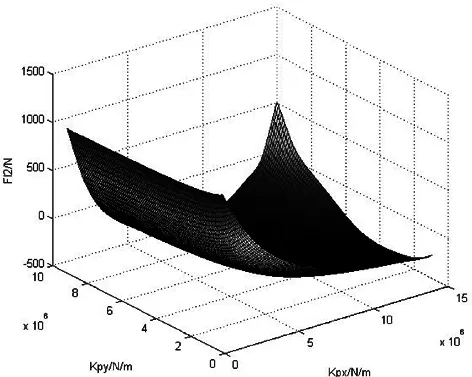
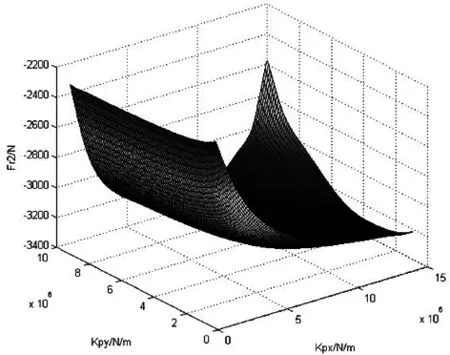
(a)2位轮对左侧　　　　(b)2位轮对右侧

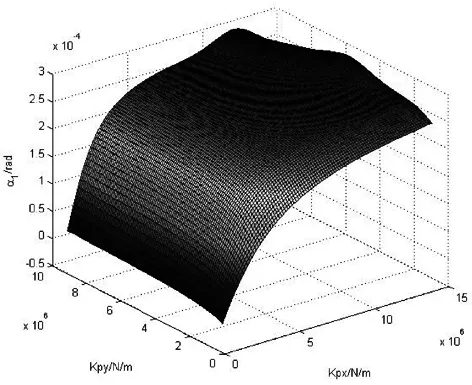
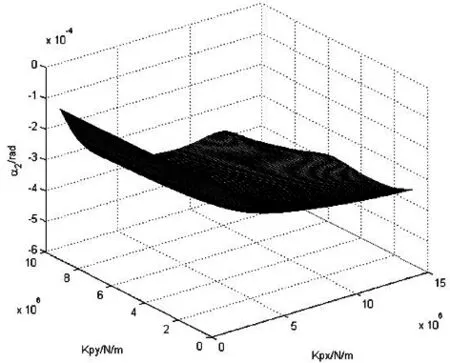
(a)1位轮对　　　　　　(b)2位轮对

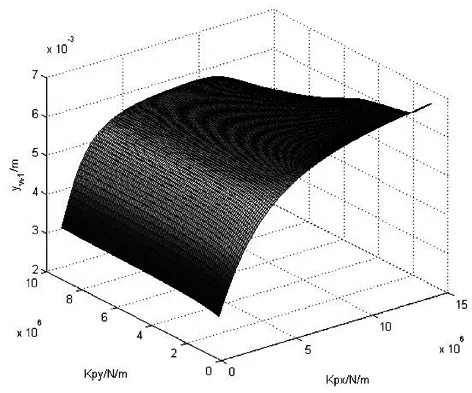
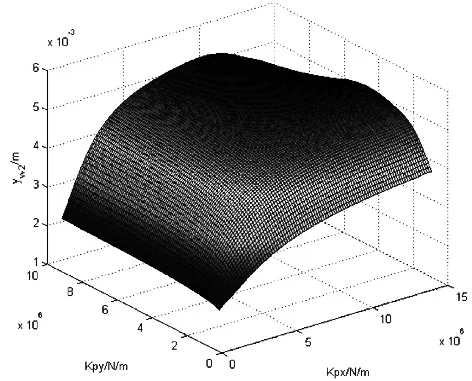
(a)1位轮对　　　　　　(b)2位轮对

由图4、图5、图6、图7可以看出：

第一，一系悬挂刚度对轮轨横向力的影响比较显著。1位轮对左侧轮轨横向力随一系横、纵向刚度值的增大而增大，右侧情况相反。左右侧横向力随Kpy的增大基本上呈线性变化趋势，并且对Kpx在较小范围内变化比较敏感，当超过一定值时，其值变化不大。

第二，当Kpx小于某值时，2位轮对左、右侧轮轨横向力随Kpy值的增减变化幅度不大，但对Kpx的变化比较敏感；当Kpx超过该值后，左、右侧轮轨横向力对Kpy的变化比较敏感，Kpx的值对其影响很小。

第三，1位、2位轮对冲角随一系横、纵向刚度值的增大而增大。随Kpy的增大基本上呈线性增长，并且对Kpx在较小范围内变化比较敏感，当超过一定值时，其值变化不大。

第四，当Kpx小于一定值时，1位、2位轮对横移量随Kpy的增大基本上呈线性增长；对Kpx在较小范围内变化比较敏感，当超过一定值时，其值变化不大。

3.2二系悬挂刚度的影响

基准参数v取35 m/s、Kpx=10 MN/m、Kpy=5 MN/m，Ksx变化范围为0.1～0.5 MN/m,Ksy变化范围取0.1～0.5 MN/m，外轨超高h大小为60 mm,曲线轨道半径R为3500 m，其余参数取基准值。

二系悬挂横向、纵向刚度对轮轨横向力、轮对冲角、轮对横移量的影响见图8、图9、图10、图11。

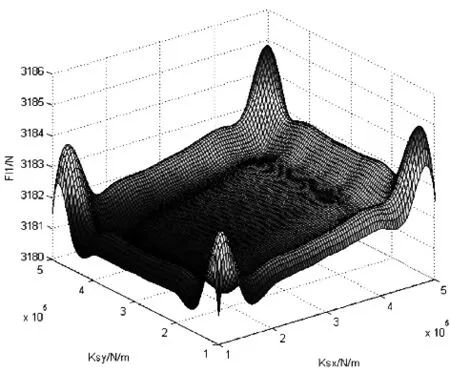
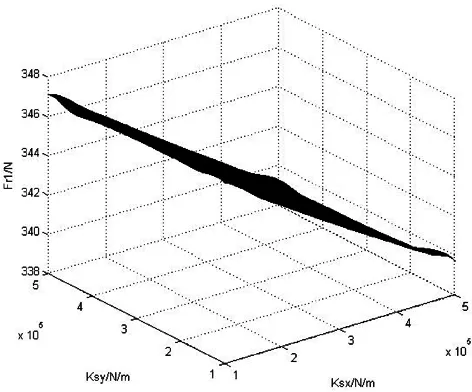
(a)1位轮对左侧　　　　(b)1位轮对右侧

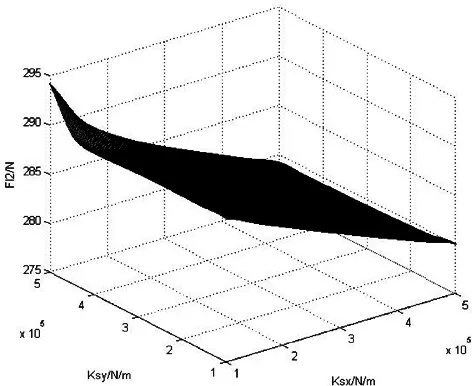
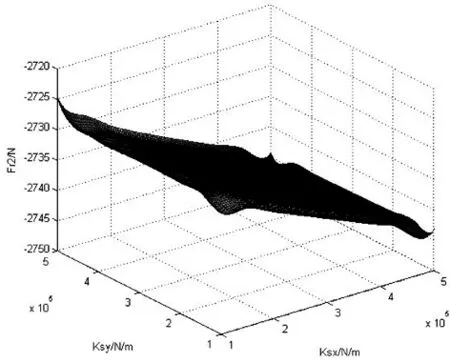
(a)2位轮对左侧　　　　(b)2位轮对右侧

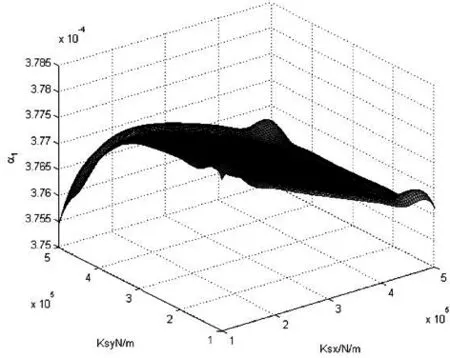
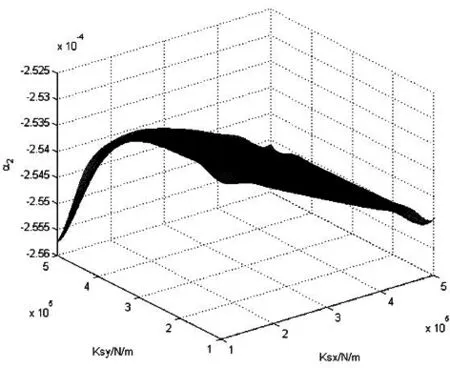
(a)1位轮对　　　　　　　(b)2位轮对

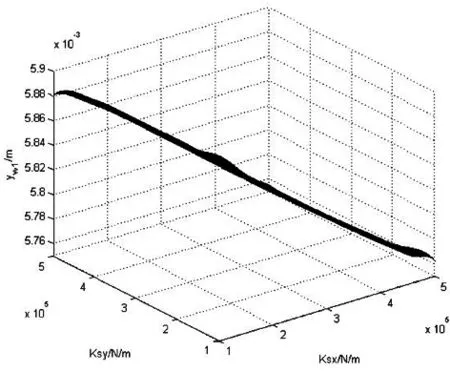
(a)1位轮对　　　　　　　(b)2位轮对

由以上各图纵坐标变化范围可以看出，车辆系统稳态曲线通过各项指标对二系横、纵向刚度值的变化不太敏感，变化幅度很小。

4结论

其一，通过“升速法”得出系统的非线性临界速度值46.5 m/s，超过非线性临界速度，系统由稳态运动发生蛇行失稳现象，各刚体相轨迹均为封闭的极限环，此时车轮与外轨发生碰撞，导致车轮及钢轨磨耗严重，甚至可能引起脱轨事故；所以，为保证曲线轨道行车安全，列车行驶速度一定不能超过非线性临界速度。

其二，悬挂刚度中一系纵向悬挂刚度对轮轨横向力、轮对冲角、轮对横移量三个指标影响最大，且对一系纵向刚度在相对较小范围内变化比较敏感；因此，要提高车辆系统曲线通过能力，应合理选取一系纵向刚度的值。

参考文献

[1]高学军，李映辉，高庆.高速客车横向稳定性及分岔研究[J].力学季刊，2009,30(4)：632-637.

[2]翟婉明.车辆-轨道耦合动力学[M].北京:科学出版社,2007.

[责任编辑：方艳]

收稿日期：2016 - 03 - 25

作者简介：马彪(1987—)，男，河南睢县人，郑州铁路局郑州动车段助理工程师。

中图分类号:U271.91

文献标志码:A

文章编号：1008-6811(2016)02-0007-03

Study on Curve Negotiation Performance and Lateral Stability of High-speed Railway Passenger Car

MA Biao

(Zhengzhou Railway Department, Zhengzhou train-set depot, Zhengzhou 450000, China)

Abstract:Aim at curve negotiation lateral vibration model of high-speed passenger car, the steady-state curve negotiation performance of vehicle system was studied based on matlab numerical simulation. The nonlinear critical speed was calculated according to speed-increasing method, and the phenomenon of hunting instability beyond the critical speed and the effects of primary suspension stiffness and secondary suspension stiffness on the lateral force of wheel/rail、wheelset attack angle and lateral displacement were investigated. Results show that the curve negotiation performance of vehicle system has a lot to do with the primary suspension longitudinal stiffness, and very sensitive to the smaller stiffness value. As for the curve track with a radius of 3500m and a superelevation of 60mm, the nonlinear critical speed of the system is 46.5m/s, which is lower than that on tangent track, and the stability reduces.

Key words:high-speed passenger car; curve negotiation；hunting motion；primary suspension；secondary suspension