一种基于合约的认知网络协作频谱共享策略

穆晓敏，师光强，刘　颖，杨守义

(郑州大学 信息工程学院， 河南 郑州450001)



一种基于合约的认知网络协作频谱共享策略

穆晓敏，师光强，刘颖，杨守义

(郑州大学 信息工程学院， 河南 郑州450001)

摘要：为解决基于合约制的多个主用户和多个次用户间的协作频谱共享问题，依据统计学的思想，提出了一种以主用户获得期望总效用最大化为目标的合约设计方法.主用户在为每个次用户设计合约时充分利用次用户接受的概率信息，得到统计意义上的期望效用，进而得到主用户期望总效用最大化的优化问题，通过理论推导化简优化问题并利用遗传算法求出次优解，即次优的合约集.数值仿真表明:通过引入统计信息成功解决了主、次用户的协作频谱共享问题，与DMA-UI算法相比，依靠统计学的方法可以使主用户在统计意义上获得更多的效用，进而提高了主用户的能效与谱效.

关键词：协作频谱共享；合约理论；非对称网络信息；多主用户；优化理论

0引言

无线通信技术和应用的迅猛发展，使得频谱资源匮乏问题日益严重.目前的固定频谱分配制度导致资源平均利用率低下，有限可用频谱和较低频谱资源利用率这一矛盾催生了认知无线电这一新技术.该技术的核心是动态的频谱共享机制，动态频谱共享允许非授权用户(次用户 SU)通过各种动态接入方式与授权用户(主用户 PU)共享频谱资源，可以有效提升频谱利用率[1-2].在基于认知的多点协作通信中，SU作为中继换取PU释放空闲频谱，双方交易的资源是频谱和功率，成交的前提是双方都有收益，收益通过构建各自的效用函数来评估,文献[3]将这种交易建模为具有激励机制的市场驱动模型.关于货币交易的频谱共享市场驱动模型，目前的研究有拍卖理论、定价理论和市场理论[4-6].该模型的应用假设是：当PU有一些空闲频谱时，货币交易的频谱共享是有效的；当PU的自身需求高或者信道容量小时，PU没有多余的频谱资源出售，交易是无效的.另外，货币交易的频谱共享需要一个可靠的计费系统，这在现实中难以实现,因此，资源交易的频谱共享是一个更好的选择[7].在基于资源交易的协作频谱共享模式中，SU为PU提供中继服务并获得PU释放的频谱资源；PU在获得链路可靠通信的同时也节省了发射功率.由此可知，基于资源交易的协作通信机制有效提升了系统整体的谱效和能效.已有的协作频谱共享研究大多集中在对称网络信息场景、单PU和多SU之间，并基于Stackelberg博弈模型[8].文献[9]针对经济学中的信息不对称场景，提出一种能够有效揭露私有信息的合约理论.文献[10] 引入合约理论构建了非对称网络信息场景下单个PU和多个SU间的协作频谱共享优化模型，以最大化系统吞吐量为目标，设计最优合约.文献[11] 研究了多个PU和多个SU间的协作频谱共享问题，针对对称网络信息场景，提出了基于匹配理论的最优解决方案；但对于非对称网络信息场景，由于SU信息是未知的，导致文献[11] 仅得到了稳定的匹配方案，故而该方案会导致PU损失过多的效用.

笔者在文献[11]的基础上，研究了非对称网络信息场景下多个PU和多个SU间协作频谱共享的优化问题.其主要贡献是提出了资源交易中的合约设计方案，并以PU总效用最大化为目标，建立了最优合约的优化及求解问题，并利用遗传算法求出次优解.数值实验结果表明:提出的基于合约理论的协作频谱共享策略能有效提高系统的能效和谱效.

1系统模型和效用函数

1.1系统模型

存在多个PU和多个SU协作频谱共享的网络模型如图1所示.该模型包含M个PU和N个SU通信链路(N>M).每条通信链路有一对收发天线.PU和SU的收发天线分别为{(PT1,PR1),…,(PTM,PRM)},{(ST1,SR1),…,(STN,SRN)}.系统协作频谱共享机制为：当PU信道条件较差时，SU为PU链路提供中继转发服务，保证PU链路的可靠通信；作为协作转发的奖励，PU释放空闲的信道资源与SU共享.以TDMA为例，PU和SU之间的协作分为3个阶段，如图1所示.

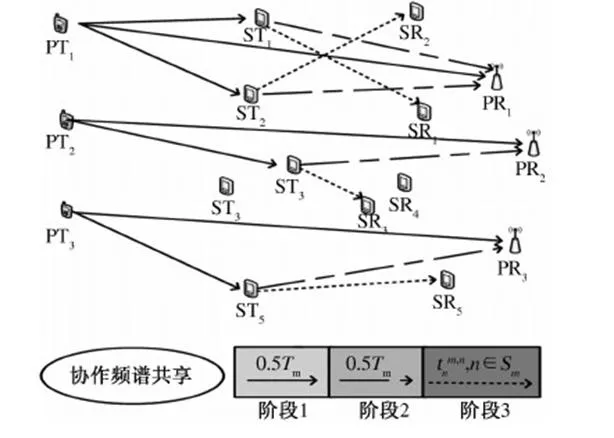
图1　系统模型Fig.1　System model

阶段1：PU发射端发送数据至对应的接收端和参与协作的SU发射端.

阶段2：参与协作的SU发射端将阶段1收到的PU数据进行放大或解码转发给PU接收端.

阶段3：参与协作的SU用PU释放的时隙资源，按TDMA的方式，发送自己的数据.

在上述协作频谱共享机制中，SU的合作意愿建立在能与PU共享时间资源，PU释放时间资源的前提是SU提供中继服务保证其链路的可靠通信.协作双方若要在资源交换中达到各自的效用最大化，均取决于是否存在有效的激励机制吸引双方积极和主动的协作.为分析该协作机制的协作收益，引入经济学中的合约理论，将PU和SU希望从资源交换中获得各自效用最大化的问题转换为最优合约的设计问题.

1.2主用户效用函数

假设SU在阶段2采用解码转发的方式，并可解码成功，且使用相同频带的中继信号之间没有干扰.记与PUm协作的SU集合为Sm；PUm为SUk(SUk∈Sm)设计的合约为(pm，k,tm，k)，其中pm，k为PUm接收端收到SUk转发信号的功率；tm，k为PUm允许SUk的接入时间.依据文献[11] PUm的效用函数Um为：

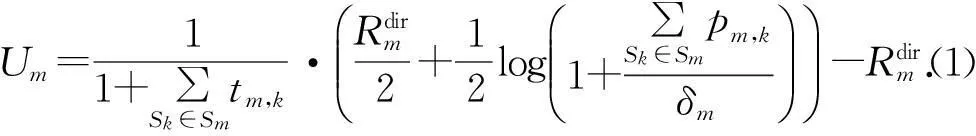
1.3次用户效用函数

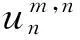
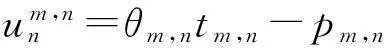
(2)

2非对称网络信息场景的最优合约

在非对称网络信息场景下，对于PUm，已知信息是网络中所有SU关于其属性值组成的集合{θm,n,1≤n≤N}，具体属性值对应的SU是未知的.不失一般性，设θm,1>θm,2>…>θm,N.

2.1最优合约的优化问题

为建立PU联合设计合约最大化PU期望总效用的优化问题，考虑到PU可以为任意个类型设计合约，由文献[10]可知，在合约不变的情况下，参与协作的SU类型越高，PU的效用越大.为最高类型(或类型值由高至低的多个)的SU设计合约是每个PU达到最大效用的必要条件.因此，优化问题转化为PUm根据其已知的{θm,n,1≤n≤N}由高至低选择nm个属性并为其设计合约，记{nm,1≤m≤M}为M个PU设计合约个数的集合.假设PUm所设计的nm个合约中，有s个合约被对应SU接受的概率为prm(nm,s)，则PUm能够获得的期望效用为0≤s≤nm所有情况下获得的效用乘以对应的概率之和，PUm为nm个属性设计合约为{(tm,1,pm,1),…,(tm,nm,pm,nm)}，PUm的期望效用的数学表达式为：

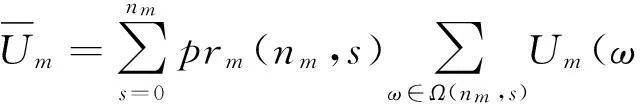
(4)

式中:Ω(nm,s)表示nm个合约有s个达成的事件集合；ω代表Ω(nm,s)中的一个事件;Um(ω)表示ω发生时，在合约{(tm,1,pm,1),…,(tm,nm,pm,nm)}下，根据式(1)得到的PUm效用.PU期望总效用函数为

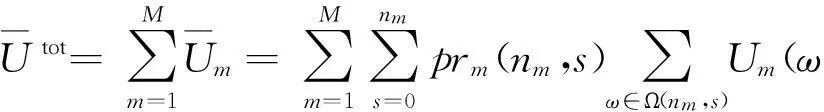
根据[10]中的定理2，PU期望总效用的优化问题可以写为

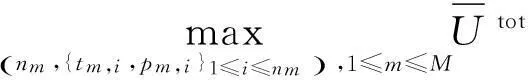
(6)

约束条件为：

条件1，对1≤m≤M，满足

条件2，对1≤m≤M，1≤k≤nm，满足

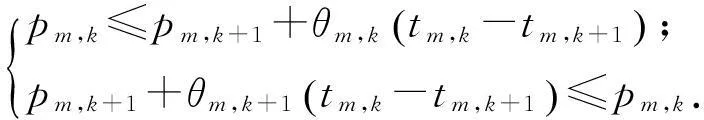
2.2优化问题的简化

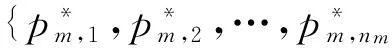
(7)

因此，式(6)可以近似简化为

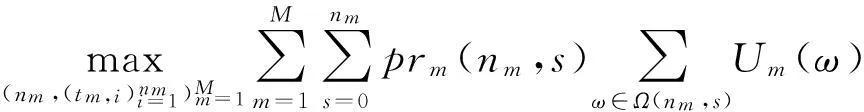
tm,1≥tm,2≥…≥tm,nm≥0, 1≤m≤M.

(8)

若SU由多个PU提供合约，SU和每个协作的概率均等，则在PU均为K(1≤K≤N)个SU设计合约条件下，单个合约被接受的概率为

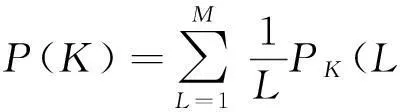
(9)

式中:PK(L)表示某个合约对应SU*被L个PU提供合约的概率，通过简单的数学推导可知：

因此，单个合约被接受的概率为

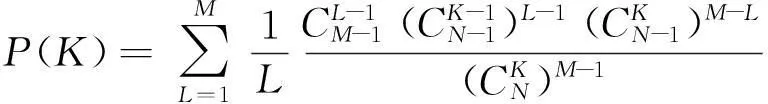
(11)

PU设计K个合约有s个被接受的概率为

pr(K,s)=P(K)s(1-P(K))K-s.

(12)

通过上述的分析，式(8)可以简化为

3数值仿真及结果分析

为了验证笔者提出的效用函数和合约设计方案的正确性及有效性，采用matlab平台对问题(13)描述的优化问题进行了数值仿真实验，并通过遗传算法求解问题(13).

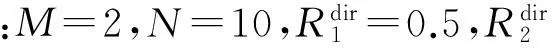
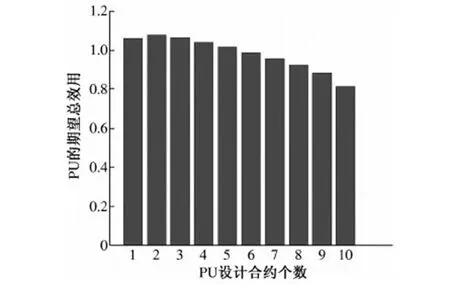
图2　PU可实现的期望总效用与设计合约个数的关系Fig.2　The relationship between PU’s expected total utility and the number of contract

网络中PU的信道环境对协作效用的影响如图3所示.基本参数设置为：M=2，N=3，SU关于PU的属性服从5～25的均匀分布.由图3可以看出，当两个PU直连速率最小时PU的期望总效用达到最大，PU的期望总效用随着PU的直连速率的增加而减小，原因是随着PU的直连速率增大，SU对PU的中继增益会逐渐减弱.

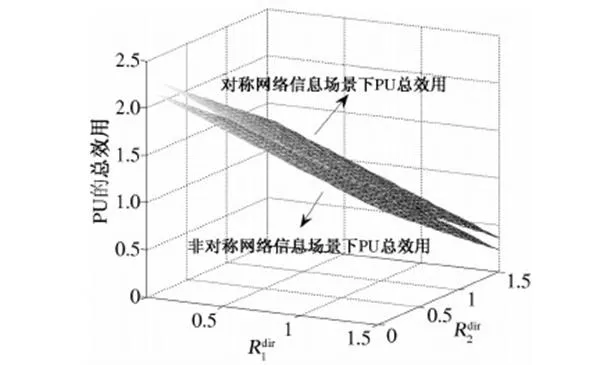
图3　PU的直连速率与PU期望总效用的关系Fig.3　The relationship between PU’s expected total utility and PU’s directional date rate

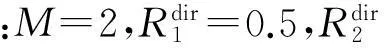
图4　本文算法与DMA-UI算法的性能比较Fig.4　The comparision between our algorithm and DMI-UI algorithm

为进一步比较本文算法和DMA-UI算法的性能，仿真参数设置同上，网络中PU对应的SU分为两类：第一类有一个SU，该SU关于PU的属性服从20～40的均匀分布；另一类关于PU的属性服从5～25的均匀分布.本文算法和DMA-UI算法比较如图5所示.由图5可以看出，笔者提出的算法优于DMA-UI算法.DMA-UI算法的思想是每个PU在获得固定效用的条件下设计单个合约，然后所有PU选择合约并告知对应的PU结果，当多于1个SU选择PU的合约时，PU会设计新的合约以让自己获得更大的效用.以此类推，至只剩一个SU选择合约时终止.当PU将效用增加至一定程度，愿意协作的SU个数减为1，由于网络中存在一个高属性值的SU，如果PU继续增加效用要求设计新的合约，该SU会继续选择协作，DMA-UI算法会停止继续增加PU效用要求，PU会损失一定的效用.

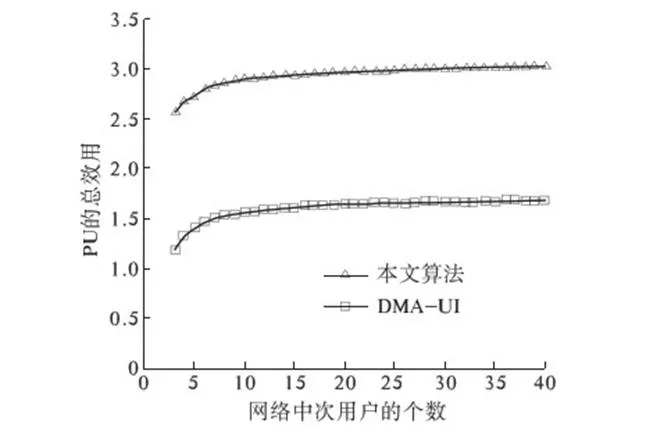
图5　本文算法与DMA-UI算法的性能比较Fig.5　The comparision between the proposed algorithm and DMI-UI algorithm

4结束语

笔者针对存在多个PU和SU的基于认知的多点协作通信网络，建立了基于合约理论的协作频谱共享模型，引入激励机制并设计了主、次用户的效用函数，提出了非对称网络场景中PU最优合约的设计方案.数值仿真验证了具有激励机制的合约设计有效提高了协作系统的总效用，从而提高了系统的能效与谱效.另外，在实际网络中PU已知的信息多是SU关于自身的属性服从的概率分布，因此，在此条件下的多个PU和多个SU的协作频谱共享问题有待进一步的研究.

参考文献：

[1]邱晶,周正.认知无线电网络中的分布式动态频谱共享[J]. 北京邮电大学学报, 2009, 32(1):69-72.

[2]王钦辉, 叶保留, 田宇,等. 认知无线电网络中频谱分配算法[J]. 电子学报, 2012, 40(1):147-154.

[3]NIYATO D, HOSSAIN E, HAN Z. Dynamics of multiple-seller and multiple-buyer spectrum trading in cognitive radio networks: A game theoretic modeling approach[J]. IEEE Trans on mobile computing, 2009, 8(8): 1009-1022.

[4]李研, 宋起柱, 赵蔚,等. 频谱拍卖机制研究[J]. 中国无线电, 2010(6):8-12.

[5]王钢, 曾禛. 定价机制下认知无线电网络频谱接入算法[J]. 哈尔滨理工大学学报, 2014, 19(2):115-119.

[6]NIYATO D, HOSSAIN E. Competitive pricing for spectrum sharing in cognitive radio networks: Dynamic game, inefficiency of nash equilibrium, and collusion[J]. IEEE Sel areas commun, 2008, 26(1): 192-202.

[7]GAO Lin, GAN Xiaoying, WANG Xinbing, et al. Cooperative spectrum sharing in cognitive radio networks:A game theoretic Approach(C)//Proc IEEE Int’l Conf on Communications.Southampton, Englad:IEEE Press, 2010: 1-5.

[8]HAN Y, PANDHARIPANDE A. Cooperative spectrum sharing via controlled amplify-and-forward relaying.[C]//Proc IEEE 19th Int’l Symp, Personal, Indoor and Mobile Radio Comm.Riviera, French:IEEE Press, 2008: 1-5.

[9]BOLTON P, DEWATRIPONT. Contract theory[M]. Boston, Massachusetts,USA:MIT Press, 2005.

[10]DUAN Lingjie, GAO Lin,HUANG Jianwei. Cooperative spectrum sharing: A contract-based approach[J]. IEEE Trans on mobile computing,2014, 13(1): 177-187.

[11]FENG Xinxin， SUN Gaofei, GAN Xiaoying, et al. Cooperative spectrum sharing in cognitive radio networks: A distributed matching approach [J]. IEEE Trans on communications, 2014, 62(8): 2651-2664.

A Contract-Based Cooperative Spectrum Sharing Approach in Cognitive Radio System

MU Xiaomin, SHI Guangqiang, LIU Ying , YANG Shouyi

(School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China)

Abstract:To solve the problem of contract-based cooperative spectrum sharing between multiple primary users and multiple secondary users, we put forward a contract design method based on statistical theory to maximize the total utility of primary users. Firstly, the primary users make full use of the accepting contract statistical information of secondary users to design a reasonable contract. Then, the primary users according to the statistical expected utility to obtain the optimization problem of maximizing theirs total expected utilities. Furthermore, we simplify the problem in theory and exploit the genetic algorithm to derive the sub-optimal solution.The simulation results and analysis show the contract design method can solve the problem of contract-based cooperative spectrum sharing successfully. Compared with the DMA-UI, the approach we formulated can make primary users obtain a higher utility, and further improve the primary users’ energy efficiency and spectrum efficiency.

Key words:cooperative spectrum sharing; contract theory; incomplete information; multiple primary users; optimization theory

收稿日期:2015-09-07；

修订日期：2015-10-30

基金项目：国家自然科学基金资助项目(61271421);河南省重大科技攻关计划项目(112102210507)

作者简介:穆晓敏(1955—)，女，河南郑州人，郑州大学教授，博士生导师，主要从事通信信号处理、认知无线研究，E-mail：iexmmu@zzu.edu.cn.

文章编号:1671-6833(2016)03-0001-05

中图分类号：TN925

文献标志码：A

doi:10.13705/j.issn.1671-6833.2016.03.001