间歇式反应釜自寻优模糊控制器设计

金东彬，潘海鹏

(浙江理工大学自动化研究所，杭州 310018)



间歇式反应釜自寻优模糊控制器设计

金东彬，潘海鹏

(浙江理工大学自动化研究所，杭州 310018)

摘要:以间歇式反应釜温度控制为目标，针对常规模糊控制参数和规则无法在线调整的问题，提出一种基于粒子群算法的自寻优模糊控制器(PSO-FC)，通过引入一个含有加权因子的规则解析式，以时间绝对值误差积分作为系统性能评价函数，利用粒子群算法对加权因子、量化因子等相关参数的取值进行智能寻优，得到一组相对最优的参数，使控制器达到较为理想的控制效果。仿真结果表明，设计的基于粒子群算法的自寻优模糊控制器具有调节精度高、过渡时间短、实时性强等特点，有较高的实用价值。

关键词：反应釜；模糊控制；粒子群算法；加权因子；温度控制

0引言

间歇式反应釜作为化工反应中的常用设备，在企业的批量生产过程中得到了广泛应用。然而由于反应釜温度控制过程中的复杂多变性，具体表现为非线性、大滞后性和时变不确定性，导致传统控制方法难以取得良好的控制效果。模糊控制根据专家经验进行设计，由于其对被控对象的模型不具有依赖性，因此可以对复杂非线性、大滞后、模型结构不确定的对象进行有效控制[1-2]。模糊控制器的性能与控制规则的制定和比例因子等相关参数的取值有很大的关系。对于常规模糊控制器，其在模糊化和逆模糊化时，相关参数主要靠设计者的经验和试凑得到，特别当控制对象的特性发生改变时，模糊控制器的相关参数和模糊规则无法相应的调整，自适应能力较弱，影响了控制的效果。

随着模糊控制理论的不断发展，当前，模糊控制常常采用与其他控制算法相结合，从而改善模糊控制器的精度。张聪彪等[3]在模糊PID控制策略的基础上，增加模糊前馈控制器，提出了一种新型的模糊复合控制策略，实现了控制系统的动态前馈补偿，改进了控制器的性能。李勇等[4]将RBF神经网络与模糊控制相结合，设计了一种新型的模糊神经网络滑动模态控制器，并针对航空发动机进行了仿真研究，结果表明，该控制器抗干扰能力较强，控制性能较好。董海鹰等[5]研究了变论域模糊控制算法，并使用多种群遗传算法对伸缩因子进行优化，仿真结果表明，该变论域模糊控制器具有较高的控制精度。白圣建等[6]研究了参数不确定的TS模糊系统，通过采用划分TS模糊区域模型的方法，以PDC原理为基础，设计了模糊区域控制器，将其应用于挠性航天器的姿态控制，仿真结果表明，TS模糊区域控制器具有鲁棒性强、控制精度高的优点。这些研究虽然在某一方面提高了模糊控制的效果，但仍然存在控制规则无法实时优化调整、适应性差等问题。

本文以间歇式反应釜为被控对象，针对其在反应过程中表现出的非线性、强滞后性和复杂不定性，提出了一种基于粒子群算法(particle swarm optimization，PSO)的自寻优模糊控制器(PSO-FC)设计方法。首先在确定系统控制器输入、输出的模糊论域之后，通过引入一个规则解析式来简化模糊推理的过程，并在规则解析式中引入加权因子，通过对加权因子的调整来达到实时调整控制规则的目的；然后以误差绝对值时间积分指标作为控制器的性能评价函数，利用粒子群算法的寻优能力，对量化因子、加权因子、比例因子等相关设定参数实施智能优化，使其获得相对较好的取值，从而使控制器获得较为理想的控制效果；最后对设计的PSO-FC自寻优模糊控制器进行仿真，以检测控制器的性能。

1基于粒子群算法的自寻优模糊控制器设计

1.1粒子群算法

粒子群算法是美国学者Eberhart和Kennedy基于鸟类觅食行为提出的[7-8]。由于该算法收敛速度较快，参数设置简单，易于实现，近年来得到了广泛的应用。

粒子群算法的原理可以描述为：在一个n 维的搜索空间中，由N个粒子组成种群 X={X1,X2,…，XN}， 设每个粒子所处位置为Xi=[xi1,xi2，…,xin]，表示一个问题的解，每个粒子都有一个自己的速度，记作Vi=[vi1,vi2，…,vin], 每个粒子在进化过程中根据式(1)和式(2)更新自己的速度，即：

vid(t+1)=ωvid(t)+c1×rand(pid-xid(t))+c2×rand(pgd-xid(t))

(1)

xid(t+1)=xid(t)+vid(t+1)

(2)

其中：vid(t+1)为第i个粒子在t+1次迭代中在d维度上的速度，xid(t+1)为第i个粒子在d维度上的位置。ω为惯性权重，c1和c2为加速常数；rand为区间[0,1]的随机数。参数ω、c1、c2的取值根据不同的控制系统需要相应确定。

1.2基于粒子群算法的自寻优模糊控制器的结构设计

图1为基于粒子群算法的模糊控制器(PSO-FC)系统结构图。图1中e为误差，Ke为e的量化因子，E为模糊化后的e的语言变量；ec为误差变化率，Kec为ec的量化因子，EC为模糊化后的ec的语言变量；α为加权因子；U为模糊控制器输出，Ku为U的量化因子，u为U逆模糊化后的输出。

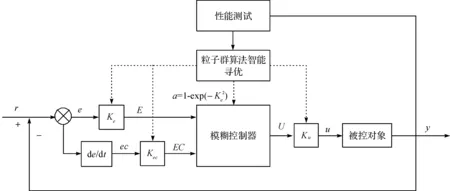
图1　PSO_FC控制器系统结构

对于双输入单输出的模糊控制器，为了使模糊规则能够根据系统的变化而实时调整，将模糊推理的过程归纳为式(3)：

U=[αE+(1-α)EC]

(3)

其中：[]代表取整运算；α为加权因子，描述误差E和误差变化率EC对模糊输出U的加权程度。

在模糊控制的过程中，通过选择不同的α取值相当于改变了控制规则。本文选择函数形式的加权因子。通常，控制目标为输出值y与设定值r相等，即e=y-r=0，因此，提出模糊化目标G：

G：使误差e靠近于0附近。

其隶属函数为：

μG(e)=exp(-Ke2)

(4)

当误差较大时，离模糊化目标G较远，隶属度值较小。当误差较小时，离模糊化目标G较近，隶属度值较大。因此，本文选择加权因子α为：α=1-μG(e)，即：

α=1-exp(-Ke2)

(5)其中k为待定参数，由粒子群算法经过优化后获得。对于模糊控制系统整体而言，模糊控制器的参数取值、模糊控制器的输出、系统的性能测试和粒子群算法的智能寻优，共同组成一个反馈回路，从而对α、Ke、Kec、Ku4个待优化的参数执行智能寻优。

1.3PSO-FC控制器实现步骤

PSO-FC控制器的实现原理为：首先对模糊控制器进行相关的初始设定，并引入含有加权因子的规则解析式，简化模糊推理的过程；然后以系统的性能评价函数为指标，利用粒子群算法对相关参数的取值进行智能寻优，找到一组相对最优的参数，使控制器获得理想的控制效果。

PSO-FC控制器具体实现步骤如下：

a)分别设定误差e、误差变化率ec、控制输出量u的隶属度函数类型和模糊论域的范围，确定加权因子α的函数形式和量化因子Ke、Kec与比例因子Ku的寻优范围。

b)以系统的性能评价函数为指标，通过PSO算法对α、Ke、 Kec、 Ku进行寻优，该步骤需要4步完成：

Step1初始化粒子群算法的相关参数，如种群规模、迭代次数、粒子维度、加速常数、惯性权重等。

Step2根据式(1)和式(2)更新粒子的位置，并根据性能测试函数计算适应度值，本文采用ITAE(即时间绝对值误差积分性能指标)作为参数优劣选择的评价函数[9-10]，ITAE可用式(6)表示：

(6)其中：T为采样周期，k为采样时刻，e(kT)为采样时刻误差。ITAE越小，表明模糊控制器的控制效果越好。

Step3根据每个粒子当前的适应度值，记录并更新自身最优值Pid和全局最优值Pgd。

Step4粒子群算法完成搜索后，输出全局最优解Pgd。

c)判断系统当前输出是否符合预期目标。若达到控制要求，则输出当前寻优的全局最值；若没有达到，则返回步骤b)继续执行。

2基于PSO-FC控制器的反应釜温度控制仿真研究

2.1PSO-FC控制器相关参数设定

本文以间歇式反应釜为对象，以温度控制为目标，通过PSO算法，对模糊控制器的相关参数进行寻优，并进行了仿真研究。其中PSO算法的参数设置如下：种群大小为40，每个粒子的维度为4，最大迭代次数为200，加速常数的取值为c1=c2=2，惯性权重的取值ω=0.6。

间歇式反应釜的温度控制具有非线性、大滞后、模型结构不确定等特性，通过建模分析，本文将反应釜温度控制对象近似为一个一阶惯性加纯滞后环节的控制模型[11-12]：

(7)

其中：试验参数比例系数A=1.2，时间常数B=80，延迟系数τ=120。

2.2PSO-FC控制效果分析

本文通过Matlab编程对PSO-FC控制器进行仿真寻优，得到相对最优的参数取值为：

K=18.17, Ke=0.05, Kec=1, Ku=0.59.

将基于该组参数设计了PSO-FC控制器应用于反应釜度温度控制过程，设定反应釜的控制温度为90℃,允许误差范围为±1℃,并将输出结果与PID控制器和传统模糊控制器(T-Fuzzy)进行了比较，各算法温度控制曲线如图2所示，控制效果比较结果见表1。

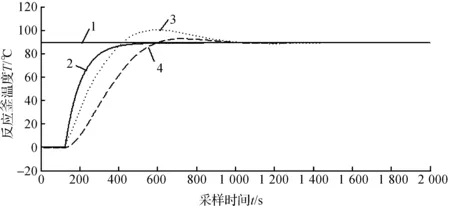
1.系统设定温度；2.基于粒子群算法优化的模糊控制(PSO-FC)；3.PID控制；4.传统模糊控制(T-FUZZY)图2　3种控制器作用下的反应釜温度响应曲线

控制器上升时间/s超调/℃调节时间/sPID21411924T-Fuzyy2967876PSO-FC1741423

由图2和表1得出，反应釜温度在PID控制器的控制下，有一个较大的超调量11 ℃，在传统模糊控制器(T-Fuzzy)的控制下，系统的超调量减小为7℃，但是响应速度较慢，系统的调节时间也改善有限，仅仅由924 s减小为876 s；而在基于粒子群算法优化的模糊控制器(PSO-FC)的控制下，系统不仅超调量减小，响应速度加快，系统的调节时间也缩短到423 s，而且调节精度优于1 ℃。仿真结果表明，本文提出的PSO-FC控制算法，温度跟随性好，控制精度高，具有较强的实用性。

3结论

本文设计的基于粒子群算法的自寻优糊控制器(PSO-FC)，凭借粒子群算法的强大寻优能力优化了控制器中的相关参数，简化了模糊控制器的设计，克服了传统模糊控制规则无法实时调整、控制参数的选择由试凑得出的不足。仿真结果表明，本文设计的控制器提高了系统的稳态精度，缩短了调节时间，改善了系统的动态性能，有较高的实用价值。

参考文献：

[1] 姜蕴珈,宋珂,章桐.基于遗传算法的增程式电动车模糊控制器设计[J].计算机工程,2014,40(7):286-290.

[2] LI L, ZHOU G. Method of variable universe fuzzy control base on inverse-model decoupling for green tea baking[J]. Transactions of the Chinese Society of Agricultural Engineering,2014,30(7):258-267.

[3] 张聪彪,杨巨生.基于类前馈解耦的双模糊控制在电站锅炉燃烧系统的仿真研究[J].计算机测量与控制,2014,22(9):2784-2788.

[4] 李勇,樊丁.基于RBF神经网络的航空发动机模糊滑模控制研究[J].计算机测量与控制,2013,21(3):632-634.

[5] 董海鹰,魏占宏,赵香桂,等.基于多种群遗传算法的电动变桨系统的变论域模糊控制[J].控制工程,2014,21(2):182-188.

[6] 白圣建,黄新生.基于TS模糊区域模型的航天器姿态控制[J].控制工程，2011,18(6):947-951

[7] BELMECHERI F, PRINS C, YALAOUI F, et al. Particle swarm optimization algorithm for a vehicle routing problem with heterogeneous fleet, mixed backhauls, and time windows[J]. Journal of Intelligent Manufacturing,2013,24(4):775-789.

[8] TING C J, WU K C, CHOU H. Particle swarm optimization algorithm for the berth allocation problem[J]. Expert Systems with Applications,2014,41(4):1543-1550.

[9] PAN F P， LIAO H K， LUO J， et al. Optimal PI controller tuning based on ITAE criterion for low-order systems with large time delay[C]// Applied Mechanics and Materials.2013,411:1716-1719.

[10] YANG Q, FU S, XUE Y, et al. Individual Intelligence Based Optimization and Its Application to ITAE Standard Forms[C]// 2014 Tenth International Conference on Computational Intelligence and Security (CIS). IEEE Computer Society,2014:109-113.

[11] 张华,沈胜强，郭慧彬.多模型分形切换预测控制在主汽温度调节中的应用[J].电机与控制学报，2014，18(2):108-114.

[12] 吴龙庭,曹顺安,胡家元.时滞系统的LM-Smith神经网络控制器[J].计算机应用研究,2014,31(4):1115-1118.

(责任编辑： 康锋)

Design of Self-optimizing Fuzzy Controller for Batch Reactor

JINDongbin，PANHaipeng

(Institute of Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Abstract：For the problem that conventional fuzzy control parameters and rules cannot be adjusted online, a self-optimizing fuzzy controller based on particle swarm optimization (PSO-FC) was proposed by taking the batch reactor temperature control as the target. Rule analysis formula including weighting factor was introduced and time absolute value error integral served as system performance evaluation function. Particle swarm optimization was used for intelligent optimizing for the values of weighting factor, weighting factor and relevant parameters to gain a group of relatively optimal parameters. Thus, the controller reached ideal control effect. The simulation result shows that PSO-FC has such features as high regulation precision, short transient time and strong instantaneity, and owns high practical value.

Key words：batch reactor；fuzzy control；particle swarm optimization；weighting factor； temperature control

DOI:10.3969/j.issn.1673-3851.2016.07.020

收稿日期：2015-10-12

作者简介：金东彬(1986-)，男，浙江绍兴人，硕士研究生，主要从事模糊控制方面的研究。

中图分类号：TP273.4

文献标志码：A

文章编号：1673- 3851 (2016) 04- 0596- 04 引用页码： 070505