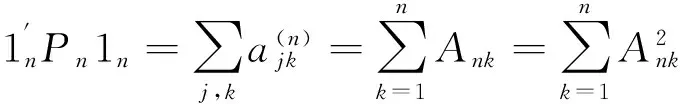Asymptotic property of two stage estimator under missing response data

LUO Shuanghua,ZHANG Yafei

(School of Science,Xi′an Polytechnic University, Xi′an 710048,China)



Asymptotic property of two stage estimator under missing response data

LUO Shuanghua,ZHANG Yafei

(School of Science,Xi′an Polytechnic University, Xi′an 710048,China)

Abstract:Under missing response data, the semiparametric regression model Y=X′β+g(T)+ε is considered to establish the two stage estimators ofn(t) and 2 of β, g(t) and σ2. Then the mean of Y is derived by the imputed every missing Yi. It is shown that these estimators have asymptotic normality andn(t) has the better convergence rate.

Key words:semiparametric regression model; two stage estimator; missing response data; asymptotic normality; best convergence rate

0Introduction

In this paper, we consider the following semiparametric regression model

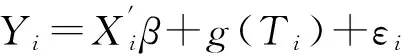
(1)

In the semiparametric regression analysis setting up, the basic inference begins by considering the random sample

(Xi,Yi,Ti,δi),

(2)

By a purely semiparametric approach to discussing the missing data (2), the MAR assumption would require that there exists a chance mechanism denoted byp(Xi,Ti), such that

P(δ=1|Xi,Yi,Ti)=P(δ=1|Xi,Ti)=p(Xi,Ti)

(3)

holds almost surely. In practice, (3) is a common assumption for statistical analysis with missing data and is reasonable in many practical applications, see reference[14].

1The two stage estimator

In this section we define the estimators that we will analyze in this paper. We describe how to estimate the regression function.

Letα=Eg(Ti),ei=g(Ti)-α+εi,i=1,…,n, the model (1) turn into following

(4)

Where thee1,…,enare independent identically distributed random variables with Ee1=0 and 0<σ2=Ee12=Eε12+Var(g(Ti))=σ02+σ12<∞. The model (4) can be changed into the following form

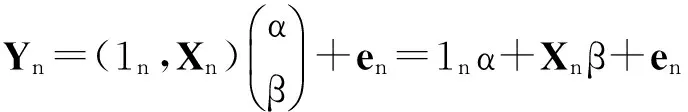
(5)

Inordertoobtainthesolutionofthefollowingleastsquaresproblem(5),wehavetofindαandβtominimize

Wn=(Yn-Xnβ-1nα)′Qn(Yn-Xnβ-1nβ).

(6)

Byoptimizationtheory,wehavethat

andthus

(7)

(8)

Now,wedefinedthenonparametricestimatorofg(t)that

(9)

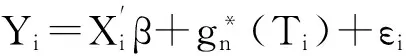
(10)

Usingthegeneralizedleastsquaresforthemodel(10),wecanfindβtominimize

(11)

andobtainestimatorofβthat

Sowenowcanobtaintheestimationofθ=E(Y).Theregressionimputationestimatorofθcanbedenotedby

(12)

Thus,wehavethepropensityscoreweightedestimator

(13)

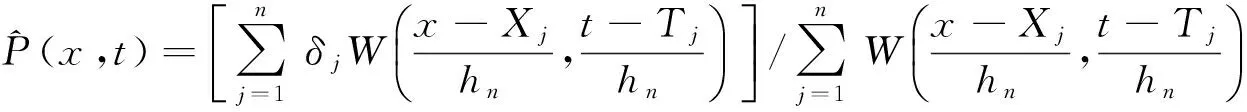
(14)

withW(·,·)istheweightingfunctionandhnisthebandwidthsequence.

2The asymptotic properties and consistencies

We explore the asymptotic distribution and consistency of the all estimators. The following notation and assumptions are needed.

(ⅰ) TheT1,T2…Tnare independent identically distributed random variables and the {Ti} is independent of the {ei}.

(ⅱ) The rank(Xn)=p

(ⅳ) E[g(T1)]2<∞.

(ⅴ) Existence 0

(ⅵ) The probability density function ofTiisr(t) and

In what follows the main results will be established for the asymptotic distribution and consistency of the semiparametric regression model.

Theorem 1Under conditions (ⅰ)～(ⅴ), we have that

Theorem 4Under conditions (i)～(vi), we have

(15)

3Sketches of the proofs

In this section, we will give the proof of Theorem 1～3.The following lemmas are needed for our technical proofs.

(6)动物园对于特殊需要的人群是否有做出详细的方案。例如：对于行动不便的老年人在遇到紧急情况时是否能够接收到及时有效的帮助；对于年幼的儿童，是否有注意到动物园护栏间距的设置与安排；对于患有突发性疾病的人群，是否能做到及时的突发的疾病进行第一时间的处理与治疗；对于残疾人群体，是否有做到设立残疾人专用设施，残疾人专用路线等，保证他们游园的安全性与便捷性等。

ProofSimilar to the theorem in reference[15].

Proof the Theorem 1Similar to the Lemma 2.1 in reference [16].

Proof the Theorem 2

(2)Firstly,weprovetheconclusion(ⅰ)of(2).

ByLemma1inreference[17],inordertoobtaintheproofof(i),weonlyprove

and

ItfollowsfromLinderbergtheoremthat

Theorem 3

(1) LetWn(t)=(Wn1(t),…,Wnn(t))′, whereti∈Cf∧{Ti,f(ti)>0}.Since

Let

(16)

whenn>p.TheCauchy-Schwarzinequalityyields

whenn≥p.Therefore,

(17)

(16)and(17)showJ2→0,a.s.Thiscompletestheproof(1)ofTheorem3.

(2)Itisnotdifficulttoobtain

and

Ithasbeenprovedthat

(18)

and

(19)

Usingthesamemethodoftheprooffor(1)ofTheorem3,itfollowsfromLemma3inreference[17]that

(20)

Bytheconditions(Ⅴ)weknowthat

and

(21)

References:

[1]ENGLE R F,GRANGER C W J,RICE J,et al.Semiparametric estimates of the relation between weather and electricity scales[J].Journal of the American Statistical Association,1986,81(394):310-320.

[2]SPECHMAN P.Kernel smoothing in partial linear models[J].J Roy Statist Soc Ser B,1988,50(3):413-436.

[3]HECHMAN N.Spline smoothing in a partly linear model[J].J Roy Statist Soc Ser B,1986,48(2):244-248.

[4]HAMILTON S A,TRUONG Y K.Local linear estimation in partly linear models[J].J Multivariate Anal,1997,60(1):1-19.

[5]WAMG Qihua,SUN Zhihua.Estimation in partially linear models with missing responses at random[J].J Multivariate Anal,2007,98(7):1470-1493.

[6]FANJ,HECKMANNE,WANGMP.Localpolynomialkernelregressionforgeneralizedlinearmodelsandquasilikelihoodfunctions[J].JournaloftheAmericanStatisticalAssociation,1995,90(47):663-685.

[7]WANGQihua,LINTONOliver,HARDLEWolfgang.Semiparametricregressionanalysiswithmissingresponseatrandom[J].JournaloftheAmericanStatisticalAssociation,2004,99(466):334-345.

[8]LIANGH.Generalizedpartiallylinearmodelswithmissingcovariates[J].JMultivariateAnal,2008,99(5):880-895.

[9]CARROLLRJ,GUTIERREZRG,WANGCY,etal.Locallinearregressionforgeneralizedlinearmodelswithmissingdata[J].TheAnnalsofStatistics,1998,26(3):1028-1050.

[10]CHENGPE.Nonparametricestimationofmeanfunctionalswithdatamissingatrandom[J].JournaloftheAmericanStatisticalAssociation,1994,89(425):81-87.

[11]WANGQ,RAONK.Empiricallikelihood-basedinferenceunderimputationformissingresponsedata[J].AnnalsofStatistics,2002,30(3):896-924.

[12]XUEL.Empiricallikelihoodconfidenceintervalsforresponsemeanwithdatamissingatrandom[J].ScandinavianJournalofStatistics,2009,36(4):671-685.

[13]XUEL.Empiricallikelihoodforlinearmodelswithmissingresponses[J].JournalofMultivariateAnalysis,2009,100(7):1353-1366.

[14]LITTLERJA,RUBLINDB.Statisticalanalysiswithmissingdata[M].NewYork:JohnWiley,1987.

[15]FANGZhaoben,ZHAOLincheng.Strongconsistencyofthekernelestimatesofnonparametricregressionfunctions[J].ActaMathematicalApplicateSinica,1985(3):268-276.

[16]CAIGengxiang.Twostageestimatorinsemiparametricmodel[J].ActaMathematicalApplicateSinica,1995,18:353-363.

[17]LUOShuanghua,XUANHaiyan,WANGYaqing.AsymptotictosemiparametricEVmodelundermissingresponsedata(inChinese)[J].JournalofHenanNormalUniversity:NaturalScience,2007,35(1):12-15.

编辑、校对：师琅

DOI：10.13338/j.issn.1006-8341.2016.02.011

Received date：2015-10-30

Foundation item:The National Natural Science Foundations(11201362);the Science Foundation of the Education Department of Shaanxi Province(14JK1305);the Natural Science Foundations of Shaanxi Province(2016JM1009)

Corresponding author:LUO Shuanghua(1976—),female,native of Suining city,Sichuan province,research area is quantile regression,missing data analysis and processing nonparametric estimations.E-mail: iwantflyluo@163.com

CLC number:O 212.7

Document code:A

缺失响应数据下二阶段估计的渐近性质

罗双华，张亚飞

(西安工程大学 理学院,陕西 西安 710048)

摘要:在缺失响应数据下考虑半参数回归模型Y=X′β+g(T)+ε,建立该模型参数β,g(t)和σ2的二阶段估计n(t)和2,并通过对每个缺失响应数据Yi进行插值,得到了响应数据的均值．研究表明,这些参数的估计具有渐近正态性,并且n(t)具有较好的收敛速度．

关键词:半参数回归模型;二阶段估计;缺失响应数据;渐近正态性;最佳收敛速度

Article ID:1006-8341(2016)02-0197-07

Citation format：LUO Shuanghua,ZHANG Yafei.Asymptotic property of two stage estimator under missing response data[J].纺织高校基础科学学报,2016,29(2):197-203.

LUO Shuanghua,ZHANG Yafei.Asymptotic property of two stage estimator under missing response data[J].Basic Sciences Journal of Textile Universities,2016,29(2):197-203.