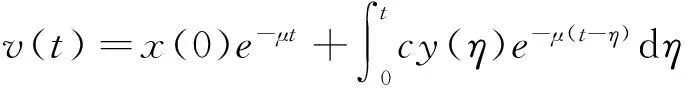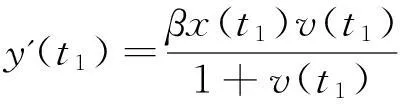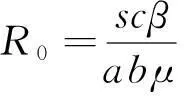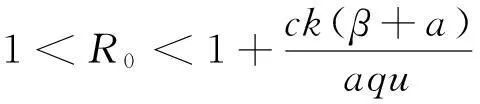一类具有免疫反应的HIV模型的稳定性*

田海燕，郭建敏，郭彩霞

(大同大学 数学与计算机科学学院，山西 大同 037009)



一类具有免疫反应的HIV模型的稳定性*

田海燕，郭建敏，郭彩霞

(大同大学 数学与计算机科学学院，山西 大同 037009)

摘要:建立了具有Holling II感染率且考虑免疫反应的HIV模型，讨论了系统解的非负性和有界性，最后通过分析模型在平衡点处相应的特征方程，利用微分方程基本理论，给出模型在感染无免疫平衡点处的稳定性.

关键词:病毒感染；稳定性；免疫反应；无免疫平衡点

0引言

目前，传染病仍然是人类身体健康的一大公敌，因为一些传染病传播速度之快，直接影响到人类的生存和发展.因此，建立传染病的动力学模型，研究其发病原因、流行规律，尤其是寻找相应的防治措施和预防策略，已经成为当今世界迫切需要解决的一个重大问题.国内外诸多学者在这方面也做了大量的研究[1-6].为了描述易感染细胞、感染细胞以及病毒颗粒之间的关系，早在1996年，学者就建立了基本的病毒动力学模型.考虑到病毒产生时存在时滞，并且对于细胞的感染率多考虑的是双线性函数，文献[2]建立了时滞动力学模型.然而要为病毒感染提供更精确的模型，免疫反应必须被考虑.免疫系统中对病毒感染有影响的两个主要反应是细胞免疫和体液免疫.细胞免疫中毒性T淋巴细胞在病毒防御中起着关键作用，因为毒性T淋巴细胞可以攻击并杀死被感染细胞，而体液免疫是基于B细胞产生的抗体来攻击并杀死被感染细胞.在一些病毒感染中，细胞免疫比体液免疫效果更好.本文在文献[2]中模型的基础上考虑了CTL的免疫作用，建立了如下的动力学模型：

(1)

1基本性质

假设系统(1)的初值为

x0=x(0)>0,y0=y(0)≥0,

v0=v(0)≥0,z0=z(0)≥0.

根据泛函微分方程的基本理论，在上述初始条件下，系统(1)的所有解都是非负的，且是有界的.即有如下结论：

定理1在上述初始条件下，系统(1)的所有解都是非负的，并且一致有界，即存在M>0使得x(t)

证明解由系统(1)的每一个方程得

y(t)=

显然x(t)>0，z(t)≥0.若y(t)>0，则有v(t)>0成立.下面证明y(t)>0.

s-de(t)

2无免疫平衡点的稳定性分析

证明系统(1)在E1处的线性化方程组为

因此，系统(1)在E1处的特征方程为

(2)

显然a1>0.因为R0>1，即scβ-abμ>0，即有

且

a1a2-a3=

3结论

参考文献：

[1]Nowak M A,Bonhoeffer S,Hill A M,et al.Viral dynamics in hepatitis B virus infection[J].Proc.Natl.Acad.Sci USA,1996,93(9):4398-4402.

[2]郑重武,张凤琴.一类具有感染时滞的HIV模型的稳定性分析[J].数学的实践与认识,2010,40(13):247-252.

[3]A M Elaiw,S A Azoz.Global properties of a class of HIV infection models with Beddington-DeAngelis functional response[J].Mathematical Metheods in the Applied Sciences,2013,36(4):779-794.

[4]A Korobeinikov.Global properties of basic virus dynamics models[J].Bulletin of Mathematical Biology,2014,66(4):879-883.

[5]张少辉,靳祯.具有非线性发生率的传染病模型性态分析[J].中北大学学报,2012,33(4):353-357.

[6]马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004.

(责任编辑:陈衍峰)

DOI:10.13877/j.cnki.cn22-1284.2016.06.015

*收稿日期：2015-11-20

基金项目：国家青年科学基金项目“纠缠及纠缠之外的量子关联刻画”(11301312)；山西大同大学青年科学基金项目“分数阶差分方程边值问题解的存在性”(2014Q10)；山西大同大学科学研究项目“高阶时滞微分方程的振动性与渐进性研究”(2015K5)

作者简介：田海燕,女,山西朔州人,教师.

中图分类号：O175

文献标志码：A

文章编号：1008-7974(2016)03-0043-03