层次分析法在大学生毕业选择中的应用
罗维喜 王娜
摘要:大学毕业生面对各种出路时,往往难以抉择,是就业、考公务员从政还是考研,每年都会使许多学生为之彷徨,迷茫。对此引进层次分析法(AHP)模型,通过对定性因素加以量化和构造判断矩阵,然后对各种可能决策方案做出评价,最后求得最佳决策,为毕业生的出路选择提供了可靠的科学依据。
关键词:层次分析法;定性因素;判断矩阵
一、建立层次结构模型
(一)假设前提
1、准则因素需符合层次分析法的结构要求。
2、考虑因素需全面。
3、短期内各层因素结构不发生变化。
(二)问题分析
运用层次分析法(AHP)对三种常见的毕业选择方式考研、就业、考公务员进行数值量化,计算系统复合指标,得到权重系数后最终采用一致性指标进行检验:
CI=λmax-nn-1
(三)决策层次分析
将决策问题分解为3个层次:最上层(目标层),最下层(方案层),中间层(用就业形势、家庭经济条件、对校园的留恋、社会交际能力、计算机英语以及其它技能等因素构造)为准则层。
(四)层对比较矩阵构造
第二层开始用成对比较法和1-9比较尺度,每次取两个因素yi和yj,用aij表示yi和yj对目标的影响之比构造成对比较矩阵:
A=(aij)n×n,aij=yiyj>1,aij=1aij(n=1,2,3…,66)
比较方案层因素Fi与Fj(i,j = 1,2,3)相对于准则层每一因素的重要性,构造对比矩阵:
Bn=F1F1F1F2F1F3F2F1F2F2F2F3F3F1F3F2F3F3
(五)权向量的计算与一致性检验
利用一致性指标、随机一致性指标以及一致性比率指标对每一个成对比较阵计算出的最大特征根及对应特征向量做一致性检验。检验对特征向量进行归一化处理后后即为权向量;若通不过检验则需重新构造成对比较矩阵。
(六)组合权向量的计算与组合一致性检验
模拟计算最下层对目标的组合权向量并做组合一致性检验。最终给出各方案对总目标影响的权重系数,最优选择对应权重最大的方案。
(七)因素判断矩阵
用aij表示因素yi与因素yj对目标Z的影响程度之比。当aij>1时,对目标Z来说yi比yj重要,反之也成立。
二、模型求解与检验
根据上述算法计算出成对比较阵A和Bn如下:
A=13/533/21/21/35/3155/25/65/91/31/511/21/61/92/32/52/111/32/926/56312/339/599/23/21
计算矩阵A的特征值与特征向量,最大特征根:λmax=6,对应特征向量:
W=(0.24020.40030.08010.16010.48040.7206)T
并根据一致性指标进行检验。
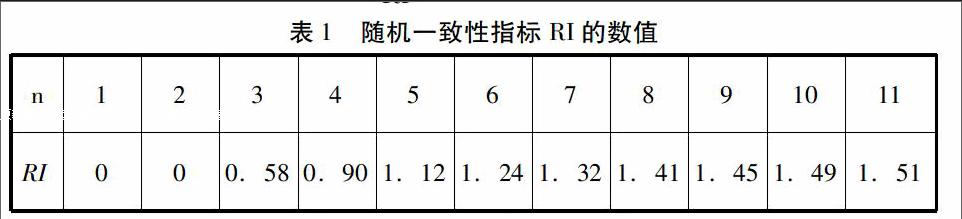
由于1,2阶的正互反阵为一致阵,所以表中n=1,2时RI=0。
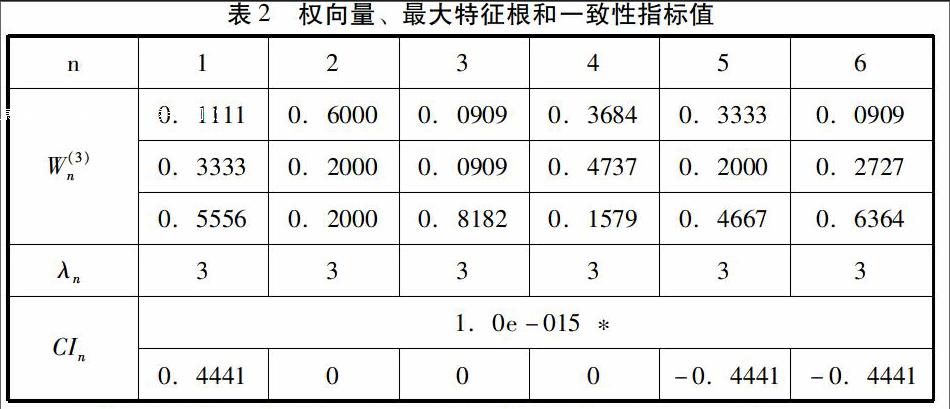
对于n≥3的比较阵A,采用一致性指标CI=λmax-nn-1检验,代入数据得:(RI见表2)CR=CIRI=0。当CR<0.1时通过检验。
同理计算F2以及F3在目标中的组合权重为0.2574和0.4742,W(3)=(0.2684,0.2574,0.4742)T,结果表明方案F3(考研)在三个选择中所占的权重为47.42%,远大于选择公务员权重0.2684和就业权重0.2574,所以应该为第一选择方向。
综上可得:利用改进的AHP法所得到的三个权重中,考研的权重最大,所以成为大学生的第一选择;而就业和考公务员的权重都远远小于考研的权重,所以它们被大学生选择的概率要远远低于考研这一选择。
从最终结果分析我们可以看出:层次分析法依靠其科学实用性和严谨性为大学生在毕业选择中提供了可靠的依据。(作者单位:1.云南冶金集团股份有限公司;2.中国人民解放军昆明民族干部学院)

