采用国外木结构持续荷载效应系数时需注意的问题与探讨

赵培焱

(四川大学建筑与环境学院, 四川成都 610065)



采用国外木结构持续荷载效应系数时需注意的问题与探讨

赵培焱

(四川大学建筑与环境学院, 四川成都 610065)

【摘要】基于加拿大的累积损伤模型，考虑欧美等国与我国地理环境、荷载分项系数等参数的取值不同。在考虑组合荷载为简化的恒载和雪荷载之后，进而采用蒙特卡洛仿真方法基于matlab得到给定木材构件在长期荷载作用下的可靠度指标进而得到持续荷载效应系数(DOL)，并提出有关问题进行探讨。

【关键词】累积损伤模型;持续荷载效应(DOL);蒙特卡洛仿真;荷载组合

1木结构持续荷载效应

我国是个文明古国，纵观历史，木结构建筑在我国建筑史长廊中留下了不可替代的地位。就木结构建筑而言，具有抗震性能好、材料来源多、结构独特等优点，但是耐火性能、抗腐朽能力差。随着现代化进程的加速，我们更应该珍惜遗留下来的木结构建筑，而当前国内对于木结构的研究以及规范等均参照欧美，所以有必要对其进行系统性的研究。木结构在长期荷载作用下其强度会降低已经被大家所公认，这一现象被称为持续荷载效应，目前国内还没有系统的方法来求持续荷载效应系数。笔者通过引用加拿大对持续荷载效应系数的方法，并考虑到国内和欧美地理条件、荷载组合、荷载概率、设计使用寿命等等的不同，对国内需要引进其方法时需要注意的问题进行了探讨。

2累积损伤模型的提出

木材强度在长期荷载作用下降低的现象被称为持续荷载效应(Durationofload简称DOL)，并为大家所熟知。早在1951年Wood就给出了木构件失效时间与应力比之间的关系曲线。紧接着美国的Gerhards在此基础上提出了木结构构件的累积损伤模型[1]，以及后来加拿大的Foschi和Barrett提出的基于损伤的木结构长期承载力模型[2]。而现在广为使用的是Foshi和Yao’s模型(Canadian模型)，也是本文之后计算DOL系数所选用的模型。以上所提到的模型均是在外界条件恒定下提出的，然而事实上，木结构长期强度还会受到空气中湿度、温度以及偶然荷载、地震等作用的影响。Fridley研究了温湿度变化对木结构长期强度的影响；Hanhijiirvi通过有限元方法研究了含水量及应力水平对其长期强度的影响[3]。到近期，有大量学者着力于研究基于随机过程和随机变量的累积损伤模型，对木结构长期强度的研究进入了一个新阶段。本文采用目前最广为使用的Canadian模型进行问题的探讨。其表达式如下：

(1)

式中:α代表损伤，变化范围从0到1，α=0代表无损伤，α=1代表构件破坏；a、b、c、n、σ0对于给定的结构构件均为常数，但是对不同构件会产生随机变化。对式(1)，τs是木构件的短期承载力，由短期荷载下的坡度测试而得；σ0定义为临界应力比，σ0·τs定义为一个临界值，只有在超过时才会有累积损伤：τ(t)-σ0·τs≤0无累积损伤；参数a由τs、b、c、n、σ0得出。

3荷载组合

一般情况下，古木建筑承受的荷载大致分为恒载和活荷载、偶然荷载。其中活荷载又有雪荷载、楼面荷载等；偶然荷载包括地震、罕见的大风等。本文为了便于后面问题的引入与讨论，暂且只考虑雪荷载和恒载的组合，今后需要考虑更多的荷载组合对其进行深入的研究。

3.1恒载

尽管一般把恒载当做不随时间和位置变化的常量，但为了研究木材的长期承载力变化，我们将其视为不能知道确切值的变量，一般视其为正态分布随机变量。

3.2雪荷载

在欧美等国，为了方便研究雪荷载对古木构件长期承载力的影响，将雪荷载分为NS·NY个阶段(NS代表每一年中的段数，NY表示构件设计使用寿命)。每一个阶段都为独立的随机变量，且每一段的荷载强度为常数，与其他每个阶段相互独立[4-5]。

3.3组合

定义d为作用在构件上恒载与恒载设计值的比值，q为作用在构件上雪荷载与设计雪荷载的比值，γ为设计恒载与设计雪荷载比值。所以有：

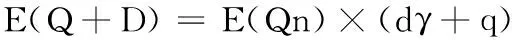
(2)

考虑荷载分项系数的极限状态方程为：

(3)

其中：φ为性能因素；R(0.05)为抗力概率分布函数中0.05分位的特征值，解式(3)有：

(4)

由式(2)、式(4)得:

(5)

当给定上述各参数的概率分布，就可以得到每个阶段雪荷载和恒载的组合值。

4基于可靠度的蒙特卡洛(monte carlo simulation)模拟

当问题涉及已知概率分布的随机变量时，就需要进行montecarlo模拟[6]。这包括重复的模拟过程，在每一次模拟中都利用由相应的概率分布生成的随机变量值，得到解的样本。MonteCarlo模拟结果无疑能够作统计处理并作各种分析，因此，montecarlo方法又称为随机模拟方法或统计实验方法。

本次仿真中，取试验构件数量为100 000，设计寿命为欧美使用的NY=30a，每一年雪荷载段数为NS=10,因为构件样本数较多，可近似认为其概率等于出现值除以样本值，而且通过计算出的失效概率，可以得出剩余寿命的可靠度指标。

(1)给定一个性能因素值φ值，以及给定设计固定荷载与设计活荷载的比值γ的值。

(2)对该方法中的每一个构件，组合荷载被分为NY·NS个阶段，在每一个阶段，设d(固定荷载比例系数)由标准正态分布的随机数计算而得，在每一个构件的整个使用阶段中为常数，在每个阶段，利用matlab选择一个0～1之间的均匀分布随机数，如果该数大于Pe，则无雪荷载，否则，另一个相同的随机变量用来计算q，所以在组合荷载下有式(5)。

(3)对每一个构件，b、c、n、σ0、τs为常数，使用循环关系αi=αi-1·Ki+Li求出α[7]。其中

(6)

(7)

(4)对功能函数G=1-α，若G≥0构件未损坏，G<0构件损坏。

(5)对该方法中所有试件重复步骤(2)、(3)过程。

(6)统计失效构件数量NFi(i为使用寿命)，得到失效概率Pf(i)=NFi/NR。

(7)可靠度指标为βi=-Φ-1(Pf(i))。

(8)对于不同的φ值重复以上过程，可以得到在不同φ值下对应的可靠度指标；

(9)由以上步骤及未考虑持续荷载效应(不考虑DOL)影响的φ-β关系图(即省略步骤(3)、(4),直接得出失效概率)可以得到目标可靠度指标下，β对应的φ1(DOL)及φ2(未考虑DOL)；

(10)定义KD=φ2/φ1，即求得DOL值。

5国内外有关条件的不同

将上述DOL计算方法引进国内需要注意的问题如本文前几部分所述，在求DOL系数时运用到了荷载的组合，以及在蒙特卡洛模拟时用到不同荷载的概率分布、样本值的抽样方法、国内外对木构件的设计使用寿命不同、国内外荷载分项系数不同(表1)。所以如若将上述方法直接引进国内将带来极大的误差，不利于工程运用，需结合我国实际对上述方法进行校正方可运用。

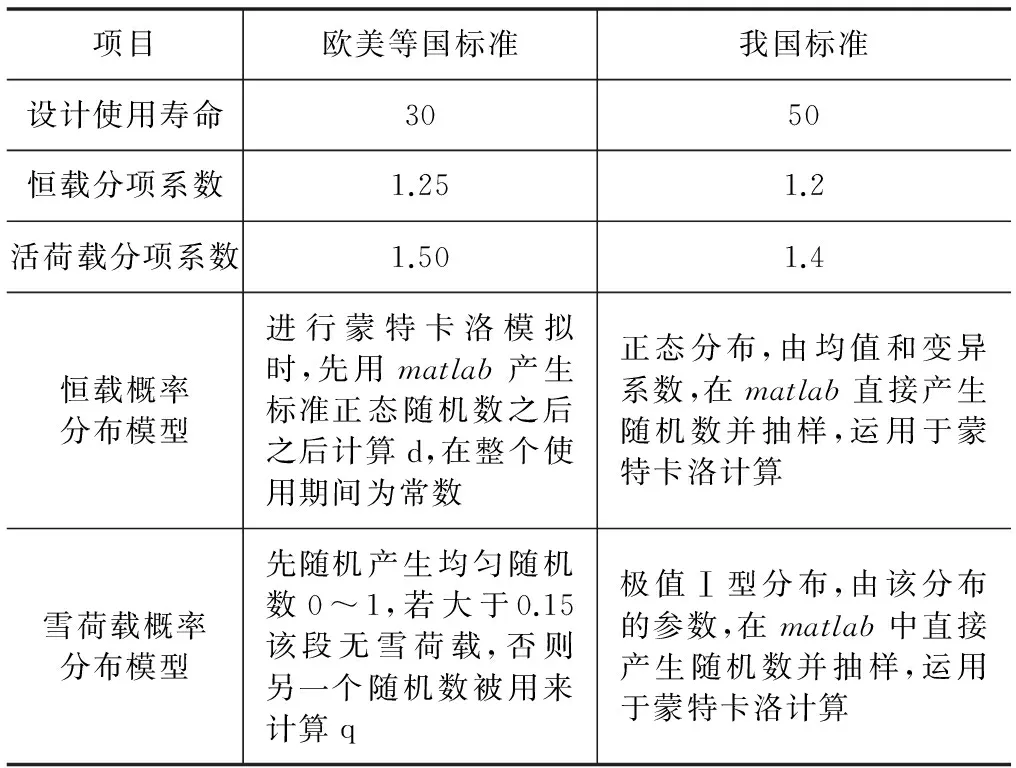
表1　国内外参数异同

6算例

在地方ottawa，木材种类为Hemlock,木材规格为No.2,2×6，为便于分析取荷载组合为恒载加雪荷载，累积损伤模型为Canadian模型，仿真方法为蒙塔卡洛法，计算工具为Matlab,模型参数见表2(数据及方法取自文献[7])。

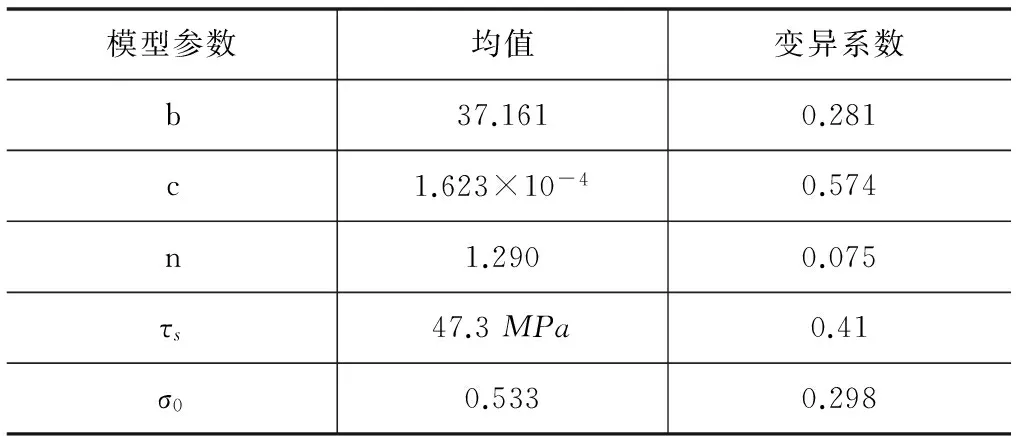
表2　累积损伤模型参数

组合荷载为：

其中:

d=D/Dn=1+Cd×Pn

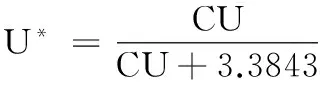
取φ=0.8，γ=0.25，蒙特卡洛模拟得到K=0.81。如果考虑表1中的不同，按以上公式分析K值走势有K1(国内)

7结论及分析

(1)当前国内还没有大量的试验来测定国内古木建筑所常用木材的累计损伤模型的参数，所以本文是参照欧美等国常用木材来进行计算，来探讨在不同地理环境、不同荷载概率分布情况下DOL的变化，今后需要更多的关于累积损伤模型的研究。

(2)木结构长期荷载下承载力降低的现象为大家公认，因此在设计时应该考虑到这一现象，对设计使用寿命进行调整，避免低估或超估木结构承载能力。

(3)本文所使用的累积损伤模型为当前最广泛使用的Canadian模型，但是随着研究的不断深入，我们还应该把影响木结构性能的其他因素综合考虑进来，如温湿度变化、腐朽、偶然作用(地震、大风)，进行更系统的研究。

(4) 由于国内外各个参数取值不一，得到K1(国内)

(5)我国是文明古国，拥有大量的古木建筑群，但由于其结构复杂，木结构本身的特性与其他材料不一样等，所以目前我国标准并不能将其存在的问题一一覆盖，需要更多的理论和实验研究来制定新的规范，以利于修缮已有木结构和设计新建木结构。

参考文献

[1]GerhardsCC.Time-relatedEffectsonWoodStrength:ALinearCumulativeTheory[J].WoodScience.1979,11(3):139-144.

[2]BarrettJD,FoschiRO.DurationofLoadandProbabilityofFailureinWood.Part1:ModellingCreepRupture[J].JournalofCivilEngineeringinCanada,1978,5(4):505-514.

[3]Hanhijiirvi.Advanceintheknowledgeoftheinfluenceofmoisturechangeonthelong-termMechanicalPerformanceofTimberStructures[J]MaterialsandStructures,2000,33(1):43-49.

[4]Sorensen,J.D.,Svensson,S.,Stang,B.F.D(2005).Reliability-BasedCalibrationofLoadDurationFactorsForTimber[J].StructuralSafety,2005,27(2):153-169.

[5]张新培.建筑结构可靠度分析与设计[M].北京：科学出版社,2001:79-85.

[6]张明.结构可靠度分析-方法与程序[M].北京：科学出版社,2009:143-148.

[7]Yao,Z.C.ReliabilityofStructurewithLoadHistory-DependentStrengthandanApplicationtoWoodMembers[M].M.A.Sc.Thesis,1987:49-56.

[8]樊承谋,安玉杰.木结构设计指南[M].北京：中国建筑工业出版社,2010:172-173.

[作者简介]赵培焱(1993～)，男，硕士，从事木结构可靠度方面的研究。

【中图分类号】TU366.2

【文献标志码】A

[定稿日期]2015-12-18