CGA优化改进型TS模糊神经网络的三级倒立摆控制

张秀玲, 郝　爽, 齐　晴, 程艳涛, 侯代标

(燕山大学 a. 河北省工业计算机控制工程重点实验室,b. 国家冷轧板带装备及工艺工程技术研究中心, 河北 秦皇岛　066004)



张秀玲a,b, 郝爽a, 齐晴a, 程艳涛a, 侯代标a

(燕山大学a. 河北省工业计算机控制工程重点实验室,b. 国家冷轧板带装备及工艺工程技术研究中心, 河北 秦皇岛066004)

摘要:针对三级倒立摆这一典型控制对象,建立了基于CGA优化的改进型T-S模糊神经网络控制器,完成了三级倒立摆的稳摆控制,将CGA与GA优化结果进行了对比,给出MATLAB仿真结果.结果表明:设计的控制器对于三级倒立摆的稳摆控制是有效的,而且CGA算法优于GA算法.

关键词:三级倒立摆; CGA; 改进型T-S模糊神经网络; 控制

在控制理论的发展过程中,仅仅通过分析来检验某一理论的正确与否以及在实际应用过程中的可行性是远远不够的,需要设计一个应用该理论的控制器,控制一个经典的对象来验证,而倒立摆恰好就是这样一个典型的被控对象.倒立摆作为一个非线性、不稳定、多变量的复杂系统,已经成为了控制领域常用的实验验证平台[1-4].

近年来,越来越多的学者对倒立摆系统进行了更为深入的研究,并在此基础上提出了诸多的控制方法,如PID网络控制[5],滑膜控制[6],自适应控制[7],LQR控制[8]等.但由于倒立摆系统自身的不确定性以及非线性特征,传统的控制理论在处理如此复杂的控制问题上表现出了不足.由此,人工智能被引入到了倒立摆的控制中来.

T-S模糊神经网络是由神经网络和模糊逻辑算法共同构成的,在自组织、自学习,知识存储以及处理不确定信息的能力方面具有不俗的表现[9-10].本文采用的改进型T-S模糊神经网络,改善了由于输入维度的增加而导致的模糊规则数目的指数增长,简化后的网络具有更加简单的结构,在三级倒立摆等多维复杂系统的控制设计上更加适用.

遗传算法(GA)是通过模仿自然界中生物进化形式和群体的整体学习过程,利用选择、交叉和变异等算子,用来求解各类复杂的优化问题[11-12].但传统GA搜索最优解的速度比较慢,参数的选取对结果影响较大,容易出现早熟现象.而且对于GA的无记忆性,通常是在以一定的概率执行完交叉、变异的操作以后,再随机产生交叉点与变异位,从而生成的下一代也是随机的,以前的知识随种群的改变而被破坏.由此可见,对于GA在进化方向上的无记忆性和随机性问题均尚未被解决.

云模型[13]是李德毅教授提出的一种运用定量和定性的方法来描述客观世界中概念的模糊性和随机性的模型,已经在智能控制等领域得到了广泛的应用.

戴朝华等人将云模型与传统遗传算法思想相结合,提出了一种新的算法:云遗传算法[14-15](CGA).CGA采用正态云模型的Y条件云生成算法实现交叉操作,基本云生成算法实现变异操作.由于云模型是一种具有稳定倾向性和随机性特点的模型,故云模型的加入,使得云遗传算法避免搜索陷入局部机制,又很好地定位全局最值,克服了传统GA的无记忆易早熟的缺点.

本文结合了改进的T-S模糊神经网络和CGA算法的优点,提出了基于CGA优化的T-S模糊神经网络控制器实现三级倒立摆的稳摆控制.该方案通过CGA的学习和训练,确定T-S模糊神经网络的权值、宽度与中心,既体现了CGA全局搜索的能力,又完美发挥了神经网络自学习的能力,为复杂非线性系统的控制提供了一条新的途径.

1三级倒立摆的数学建模

三级倒立摆主要由小车、摆杆1、摆杆2和摆杆3组成,它们之间由转轴自由链接,由电机驱动的小车,在皮带牵引控制下在水平轨道上作直线运动,光电码盘可以将测量得到的信号转换成为小车的位置量与摆杆的角度量;在轨道所在的铅垂平面内,各级摆杆可以绕各自的转轴自由转动.

三级倒立摆是一个复杂的系统,难以直接建模,但在忽略一些不重要的因素后,倒立摆系统就简化为一个典型的运动刚体系统,可以将其置于惯性坐标系内,如图1所示,应用经典力学建立系统的动力学方程.

图1　三级倒立摆的简化结构

这里规定顺时针方向的转角和力矩为正方向,并约定:x为小车位移,u为外界作用力,θi为摆杆i与铅垂线方向的夹角,Li为摆杆i的长度,Oi为摆杆i连接点的位置,M为小车质量,Mi为连接摆杆i与摆杆i+1质量块的质量,mi为摆杆i的质量,li为Oi到摆杆i质心的距离,c0为小车与导轨之间的摩擦系数,ci为摆杆i绕Oi转动的摩擦系数,其中i=1,2,3,具体参数如表1所示.

表1　三级倒立摆系统实验参数

采用GLIP-2003型的三级倒立摆系统,利用分析力学的Lagrange方程:

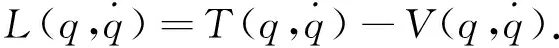
(1)

式中,L表示拉格朗日算子;q表示系统的广义坐标;T表示系统的动能;V表示系统的势能.拉格朗日方程由广义坐标qi和L表示如下:

(2)

式中,q=[x,θ1,θ2,θ3],τ表示系统沿该广义坐标上的广义外力.经推导可得到以下方程:

(3)

(4)

(5)

(6)

式中

(7)

(8)

(9)

(10)

本文采用直接使用式(7)～式(10)在Simulink中搭建精确的非线性模型,如图2所示.该方法未对数学模型做任何简化,是一种精确的模型,能够更好地检验控制方案的有效性.

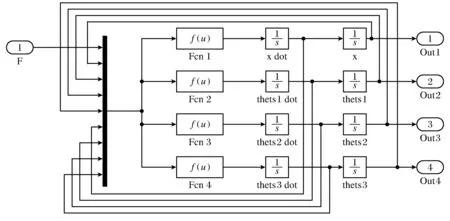
图2　三级倒立摆Simulink模型

常见的T-S模糊神经网络通常由前件网络与后件网络组成,前件网络用来匹配模糊规则的前件,后件网络用来产生模糊规则的后件.但是由于前件网络中的模糊规则数目没有合理的确定方法,规则层的节点也就无法给定.通常情况下,采用输入变量个数的子数形式,该方法导致了冗余模糊规则的出现,既影响网络的收敛性能和速度,又在一定程度上降低了网络的收敛精度.

本文采用改进的T-S模糊神经网路,改进后的网络,前件部分由原来的4层减少为3层,与此同时,模糊规则层节点的数目也相应地减少,使得网络具有更快的学习速度[16].根据三级倒立摆模型,设计了改进后的T-S模糊神经网络控制器,结构如图3所示.该网络设计是一个9输入,1输出的结构,输入部分除固定值1外,其余8个分别为三级倒立摆的8个状态量,输出部分为倒立摆的输入力矩,其中i=1,2,…,5;j=1,2,…,8.

改进型T-S模糊神经网络同样由前件网络与后件网络构成.改进后的前件网络有三层:

第一层作为输入层,与各个节点连接的分别为与之对应的输入变量,本层节点的个数为8个.

第二层作为模糊化层,这一层中节点个数与模糊划分数相同,这里划分为5个,每个节点即代表一个语言变量,用于将输入变量模糊化.模糊隶属度采用的是高斯函数:

(11)

式中:cij为隶属度中心;λij为隶属度函数宽度.

图3　TS模糊神经网络结构

第三层作为模糊规则层,每个节点就是一条模糊规则,对于每条规则适应度的计算,通常采用代数乘积算法,即

(12)

本层节点的个数就是模糊划分数m,比改进前的节点数mn有了极大程度地减少,这一改进既防止了冗余规则的出现,又加快了前件部分的学习速度.

后件部分,各层之间采用的是线性计算,故后件部分网络结构未做改进,其隐含层输出为

(13)

其中,i=1,2,…,5.

网络的总输出为

(14)

3.1云模型

云模型是一种用语言值表示定性概念与其定量表示之间的不确定性转换的模型,反映的是客观世界随机性与模糊性的关联性,形成了定性与定量之间的映射[13].

定义设有一个用精确数值表示的定量论域U,T是U上的定性概念,如果存在一个定量值x∈U,而且x是定性概念T上的一次随机实现,x对T的确定度μ(x)∈[0,1]是一个有稳定倾向的随机数.

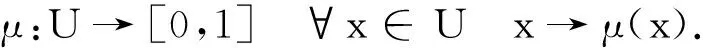
(15)

那么,x在定量论域U上的分布就称为云模型. 云模型通常用3个数字特征来表示一个概念, 分别为期望Ex, 熵En及超熵He,如图4所示.Ex反映了云层的中心位置,En反映的是云滴离散程度以及云层陡峭程度,He反映了云层厚度.

图4　云模型的数字特征示意图

3.2云遗传算法

对于传统的GA算法,由于其在搜索最优解的计算过程中,速度较慢,而且在参数的选取上,对结果影响也比较大,容易出现早熟的现象,此外GA算法又是无记忆的算法,基于以上缺点,本文提出了云遗传算法(CGA).云遗传算法中,云发生器是一种用于生成云滴的算法,传统的遗传算法结合云模型,采用正向正态云发生器[14]实现变异操作,Y条件云发生器[14]实现交叉操作,形成的一种全新的算法.

利用CGA优化的基本流程如图5所示.首先根据三级倒立摆稳摆控制这一实际问题进行相关参数设置,初始种群随机形成;将三级倒立摆模型带入T-S模糊神经网络控制系统中进行适应度计算,通过选择、交叉及变异操作的不断循环,将较差的个体淘汰,直到满足终止条件,得到网络最优解,确定最终参数.

本文在对T-S模糊神经网络控制器进行优化的过程中,选择初始群体个数为40,交叉概率为0.9,变异概率为0.1,优化参数个数为125个,算法采用目标函数适应度最小作为训练准则.

图5　CGA优化过程

CGA优化结果如图6所示.

3.3三级倒立摆的稳摆控制系统设计

改进后的T-S模糊神经网络在进行三级倒立摆系统控制时,与一般的神经网络类似,通过CGA优化网络参数,包括权值,中心值及宽度,使适应度值即控制系统状态量的均方差达到最小,从而得到参数确定的三级倒立摆稳摆控制器.改进的T-S模糊神经网络控制系统如图7所示.

图6　CGA优化结果

图7　TS模糊神经网络控制系统

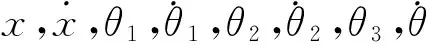
4仿真验证

为了验证CGA优化的改进型T-S模糊神经网路控制器在三级倒立摆的稳摆控制上的有效性,将上文Simulink得到的三级倒立摆模型代入到设计好的控制系统中来,经过网络学习与训练,得到控制仿真结果.这里为了检验CGA的优越性,将GA的优化结果作为对比,得到三级倒立摆的稳摆控制效果对比图,如图8所示.

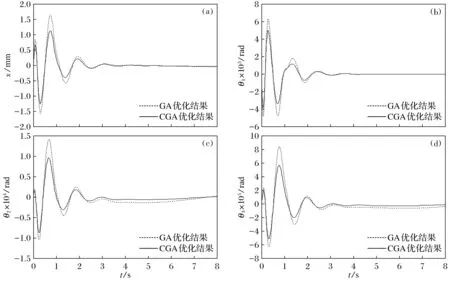
图8　三级倒立摆控制结果

图8的4个图分别表示小车位移、下摆杆角度、中摆杆角度及上摆杆角度的控制结果.从图中可以直观地看出,采用CGA优化的T-S模糊神经网络控制器在对三级倒立摆进行稳摆控制上是有效的,而且其控制结果要优于GA优化得到的控制器.

5结论

本文针对高阶恒不稳定的三级倒立摆系统,设计了CGA优化的T-S模糊神经网络控制器,实现了三级倒立摆的稳摆控制,发挥了CGA全局寻优的优势,且克服了GA无记忆易陷入局部机制的缺点,得到了很好的控制效果.仿真结果表明,基于CGA优化的T-S模糊神经网络控制器具有适应面广,不易陷入局部机制,收敛迅速的优点,对于复杂系统而言,提供了一种非常有效的控制方法.

参考文献:

[ 1 ]GLÜCKT,EDERA,KUGIA.Swing-upcontrolofatriplependulumonacartwithexperimentalvalidation[J].Automatica, 2013,49(3):801-808.

[ 2 ]LIUB,HUH.GroupdelayinducedinstabilitiesandHopfbifurcations,ofacontrolleddoublependulum[J].InternationalJournalofNon-LinearMechanics, 2010,45(4):442-452.

[ 3 ]LIZS,DANYH,ZHANGXC,etal.Fulfillmentofarbitrarymovementtransfercontrolbetweenequilibriumstatesforadoublependulumrobot[J].ActaAutomaticaSinica, 2010,36(12):1720-1731.

[ 4 ]DOKD,SEETG.Motioncontrolofatwo-wheeledmobilevehiclewithaninvertedpendulum[J].JournalofIntelligent&RoboticSystems, 2010,60(3):577-605.

[ 5 ] 张秀玲,樊红敏,臧佳音,等. 三级倒立摆的GA-PIDNN系统辨识[J]. 沈阳大学学报(自然科学版), 2014,26(2):113-118.

(ZHANGXL,FANHM,ZANGJY,etal.GA-PIDNNsystemidentificationfortripleinvertedpendulum[J].JournalofShenyangUniversity(NaturalScience), 2014,26(2):113-118.)

[ 6 ] 邱德慧,王庆林,杨洁. 倒立摆系统的动力学建模与滑模控制[J]. 控制工程, 2012(S1):8-14.

(QIUDH,WANGQL,YANGJ.Dynamicalmodelingandslidingmodecontrolofinvertedpendulumsystems[J].ControlEngineeringofChina, 2012(S1):8-14.)

[ 7 ] 蔺小林,邓雄峰,李露. 基于参数自适应模糊PI的三级倒立摆控制[J]. 控制工程, 2015,22(3):404-408.

(LINXL,DENGXF,LIL.ControlfortripleinvertedpendulumbasedonparameteradaptivefuzzyPI[J].ControlEngineeringofChina, 2015,22(3):404-408.)

[ 8 ] 刘文秀,郭伟,余波年. 倒立摆状态反馈极点配置与LQR控制Matlab实现[J]. 现代电子技术, 2011,34(10):88-90.

(LIUWX,GUOW,YUBN.DesignofstatefeedbackpoleplacementandLQRcontrollerforinvertedpendulumbasedonMATLAB[J].ModernElectronicsTechnique, 2011,34(10):88-90.)

[ 9 ]SANGY,XUC,LIUB,etal.TSfuzzyneuralnetworkalgorithmapplicationinnonlinearcontrol[C]∥Proceedingsofthe2011,InternationalConferenceonInformatics,Cybernetics,andComputerEngineering(ICCE2011)November19-20, 2011,Melbourne,Australia.Berlin:SpringerBerlinHeidelberg, 2012:165-172.

[10] 张莹. 一类不确定T-S模糊系统的H∞控制器设计[J]. 沈阳大学学报(自然科学版), 2014,26(2):169-172.

(ZHANGY. H∞controlofT-Sfuzzysystemswithrealparametricuncertainty[J].JournalofShenyangUniversity(NaturalScience), 2014,26(2):169-172.)

[11] 马永杰,云文霞. 遗传算法研究进展[J]. 计算机应用研究, 2012,29(4):1201-1206.

(MAYJ,YUNWX.Researchprogressofgeneticalgorithm[J].ApplicationResearchofComputers, 2012,29(4):1201-1206.)

[12] 袁满,刘耀林. 基于多智能体遗传算法的土地利用优化配置[J]. 农业工程学报, 2014,30(1): 191-199.

(YUANM,LIUYL.Landuseoptimizationallocationbasedonmulti-agentgeneticalgorithm[J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2014,30(1):191-199.)

[13] 刘常昱,李德毅,杜鹢,等. 正态云模型的统计分析[J]. 信息与控制, 2005,34(2):236-239,248.

(LIUCY,LIDY,DUY,etal.Somestatisticalanalysisofthenormalcloudmodel[J].Informationandcontrol, 2005,34(2):236-239,248.)

[14] 戴朝华,朱云芳,陈维荣. 云遗传算法[J]. 西南交通大学学报, 2006,41(6):729-732.

(DAICH,ZHUYF,CHENWR.Cloudtheory-basedgeneticalgorithm[J].JournalofsouthwestJiaotongUniversity, 2006,41(6):729-732.)

[15] 郑小强,刘敏,孔繁荣,等. 基于云遗传算法的MRO服务调度[J]. 计算机集成制造系统, 2013, 19(9):2348-2354.

(ZHENGXQ,LIUM,KONGFR,etal.CloudgeneticalgorithmbasedMROservicesschedulingmodel[J].ComputerIntegratedManufacturingSystems, 2013,19(9):2348-2354.)

[16] 干思权,刘贺平,申祝江. 一种改进型T-S模糊神经网络[J]. 控制工程, 2005,12(5):442-445.

(GANSQ,LIUHP,SHENZJ.AnimprovedT-Sfuzzyneuralnetwork[J].ControlEngineeringofChina, 2005,12(5):442-445.)

【责任编辑: 李艳】

Improved T-S Fuzzy Neural Network Control System by CGA for Triple Inverted Pendulum

ZhangXiulinga,b,HaoShuanga,QiQinga,ChengYantaoa,HouDaibiaoa

(a. Key Laboratory of Industrial Computer Control Engineering of Hebei Province, b. National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, Yanshan University, Qinhuangdao 066004, China)

Abstract:Aiming at the typical control object of the triple inverted pendulum, an improved T-S fuzzy neural network controller, which optimized by CGA, is proposed to make the triple inverted pendulum stay stability. Comparing the optimization results of CGA and GA from the MATLAB simulation, the results show that the proposed controller optimized by CGA is effective in triple inverted pendulum control.

Key words:triple inverted pendulum; CGA; improved T-S fuzzy neural network; control

文章编号:2095-5456(2016)03-0206-07

收稿日期:2015-12-09

基金项目:国家自然科学基金资助项目(61007003); 河北省自然科学基金-钢铁联合研究基金资助项目(E2015203354); 河北省教育厅科学研究计划河北省高等学校自然科学研究重点项目(ZD2016100); 燕山大学研究生教育教学改革项目(JG201506); 燕山大学电气工程学院研究生教改项目(DYY2015).

作者简介:张秀玲(1968-),女,山东章丘人,燕山大学教授,博士.

中图分类号:TP 273

文献标志码:A