煤矿工作面顶板倾斜钻孔疏放水井流计算方法

陈　实，董书宁，李竞生，王　皓，杨　建

(1．中煤科工集团西安研究院有限公司，陕西西安　710054;2．陕西省煤矿水害防治技术重点实验室，陕西西安　710077)



煤矿工作面顶板倾斜钻孔疏放水井流计算方法

陈实1，2，董书宁1，2，李竞生1，王皓1，2，杨建1，2

(1．中煤科工集团西安研究院有限公司，陕西西安710054;2．陕西省煤矿水害防治技术重点实验室，陕西西安710077)

摘要:以顶板疏放水中常用的倾斜钻孔为对象，以空间点源理论为基础，运用反映法，建立了均质各向异性无限水平承压含水层中非完整倾斜钻孔的井流计算方程，讨论了多个倾斜钻孔同时工作时，多孔叠加的疏放水井流计算方法。在此基础上，运用陕北某矿顶板含水层疏放水工程实例，验证了此方法的有效性。形成了一套集分析、模拟、预测为一体的倾斜钻孔疏放水计算方法。

关键词:倾斜钻孔;顶板疏放水;井流计算;煤矿工作面;解析解

陈实，董书宁，李竞生，等．煤矿工作面顶板倾斜钻孔疏放水井流计算方法［J］．煤炭学报，2016，41(6):1517－1523．doi:10．13225/ j．cnki．jccs．2015．0901

Chen Shi，Dong Shuning，Li Jingsheng，et al．Analytical solution for slanted well in the roof of coal mine working face［J］．Journal of China Coal Society，2016，41(6):1517－1523．doi:10．13225/j．cnki．jccs．2015．0901

煤矿顶板水害是煤矿建设与生产中的主要灾害之一，频发的煤矿顶板突水造成了极为惨重的人身伤亡和经济损失，已成为制约煤矿安全生产的瓶颈，而开展顶板疏放水是预防这一灾害的关键。在众多的疏放水技术中，倾斜钻孔疏放水因其施工难度低、疏放效率高，已作为一项成熟的煤矿水害防治技术，在煤矿防治水特别是在煤矿顶板水害防治中得到了广泛的应用。

煤矿井下施工的倾斜疏放水钻孔开孔位置与钻孔轨迹有别于通常的水文地质供水井。井下疏放水钻孔开孔位置通常布置在煤矿工作面运输巷和回风巷道所处的煤层或煤层顶底板中，钻孔穿过煤层顶板倾斜进入含水层。因此，现有的井流计算方法在计算煤矿倾斜钻孔井流时都具有一定的局限性。

现有井流计算方法中，以钻孔从地面垂直进入含水层的垂直井流计算方法发展较早且较为成熟，这些方法在煤矿防治水中已有了大量应用［1－2］。2009年，王旭升和万力［3］对这些方法进行了归纳;孙讷正［4］、李竞生和姚磊华［5］、薛禹群［6－7］、陈崇希［8］运用解析解开展了含水层参数识别方法研究。詹红兵和万军伟［9］针对含水层中的水平钻孔推导了系列水平井流计算方程。

然而，无论是垂直井流计算方程还是水平井流计算方程，应用于煤矿井下倾斜钻孔疏放水的计算中，往往与生产实践有较大的背离。造成疏水量过小煤矿工作面被淹，或者疏放水过多水资源浪费的现象。

倾斜钻孔井流计算方法研究最早起源于石油斜井产能计算。本文参考了Cinco－Ley［10］推导的计算石油斜井产能的解析方程，建立了含水层中倾斜钻孔疏放水的井流方程。推导过程中考虑了石油斜井产能解析方程未涉及的渗透系数各向异性条件。建立的解析解方程同时适用于完整井和非完整井流计算。

建立的倾斜钻孔疏放水井流的计算方法将为准确预测倾斜钻孔疏放水量、疏放水时间、控制疏放水降深提供科学依据，对防治煤矿顶板水害具有重要意义。

1　倾斜钻孔井流计算方程推导

1.1承压含水层倾斜钻孔理想模型

图1展示了承压含水层中一个倾斜钻孔的三维概念模型。含水层为均质各向异性，坐标系的原点位于含水层底板(倾斜钻孔竖直与水平的中点位置)。含水层厚度为M，且在水平平面上无限延伸。钻孔的长度为Lw，从含水层的下边界至钻孔中点的测得的距离为Zw，如图1所示。图中θ为观测点和坐标原点连线在水平面上的投影与r轴的夹角，θw为钻孔与水平方向的夹角。θw=90°表示垂直井的特殊情况。笔者不考虑水平井的情况，方程中θw≠0。

据以上条件作出如下假定:

(1)含水层是均质、各向异性、等厚且水平分布，含水层为弹性体;

(2)无垂向补给、排泄，即W=0;

(3)渗流满足达西定律;

(4)钻孔可以是完整井也可以是非完整井，假定流量沿井壁均匀进水;

(5)水头下降引起地下水从储存量中的释放是瞬时完成的;

(6)疏放水前水头面水平;

(7)井径无限小且定流量疏放水;

(8)含水层侧向无限延伸。

由于套管和滤管的作用，钻孔的导水段可以在含水层的任意位置倾斜任意角度。

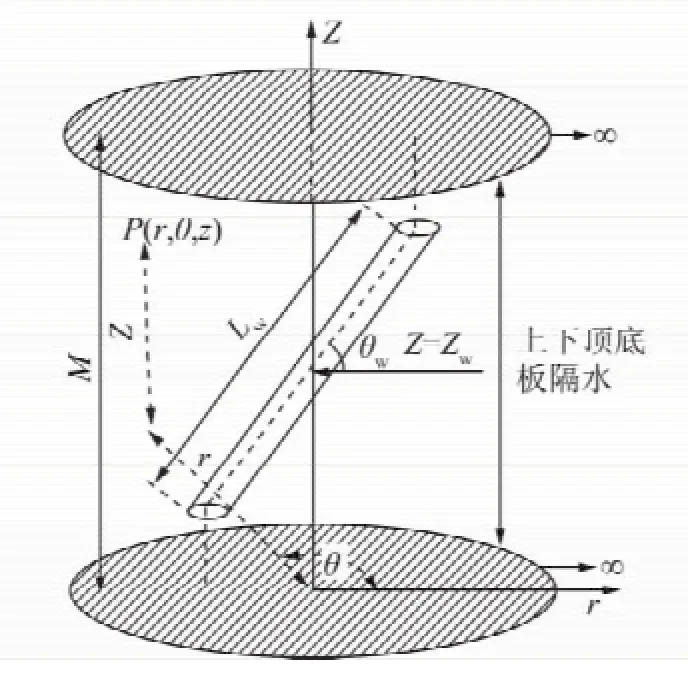
图1　承压含水层中部分止水的倾斜钻孔示意Fig.1　Slant well in confined aquifer with part sealing

1.2空间瞬时点汇

1884年，L.Kelvin在研究热传导的理论中［6］，对均质各向同性无限介质中一瞬时空间点源作用下温度的分布规律提出一个基本解。这个解成为研究地下水的井流的一个重要方法——源汇法的基础(图2)。

将Kelvin的解拓宽到各向异性介质，在强度为Vp的瞬时点汇作用下，无限空间中任意观测点P(r，z，t)处水头降深的分布规律可以表示为

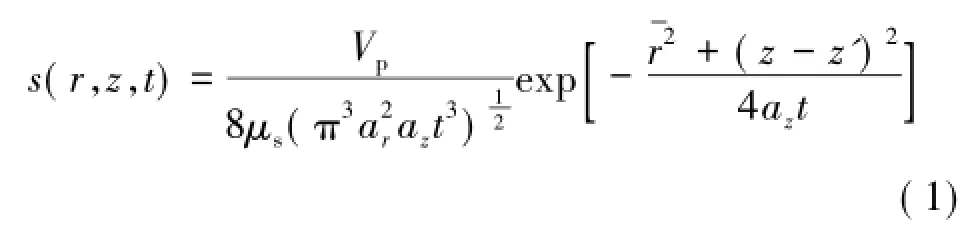
式中，s(r，z，t)为观测点P处t时刻的水头降深;r为观测点P与空间点汇水平方向的距离;z为观测点P与空间点汇垂直方向的距离;t为从瞬时疏放水开始至观测时的时间;Vp为空间点汇的瞬时点汇的强度，即点汇瞬时抽取的水的体积;μs为给水度;ar=Krr/μs为含水层水平方向的压力传导系数;az=Kzz/μs为含水层垂直方向的压力传导系数;Krr和Kzz分别为水平方向和垂直方向的渗透系数;为坐标变换后将各向异性含水层等效为各向同性含水层的观测点径向坐标;(0，z')为瞬时点汇在z轴上的位置。

式(1)为观测点P处水头降深的二维空间解，其意义为，在无限均质各向异性的空间(含水层)中，当t=0时，在点(0，z)处有一井径趋于0的球状井瞬时抽取地下水体积Vp后，t时刻在(r，z)处引起的水头降深s。对于注水井，s和Vp均取负值。

1.3空间瞬时线汇

建立三维空间柱坐标系，纵轴为z轴，水平面为极坐标系。柱坐标系中在(r，0，z)平面上存在长为Lw，与水平方向夹角为θw，中点坐标为(0，0，zw)的瞬时线汇(图3)，线汇上瞬时疏放水强度为V。在线汇上取一极小段，设其纵向长度为dzp。当dzp→0时，则微分线汇dzp的瞬时强度为VL=V/dzp。方程式(3)即为在微分瞬时线汇dzp(可视为瞬时点汇)的作用下，三维空间中观测点P(r，θ，z)处的微分降深。

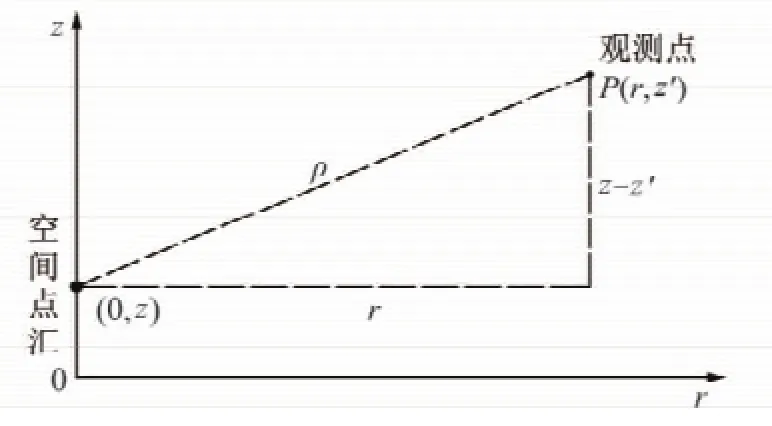
图2　瞬时空间点汇及观测点的位置Fig.2　Instantaneous sources point and observation point

图3　无限空间含水层倾斜线汇及观测点的位置Fig.3　Infinite space aquifer slanted line sinks and observation points

根据初始假定，该定解条件可写成

式中，H(r，θ，z)为P点处水头降深;H0为含水层初始水头高度;θ为观测点与坐标原点的夹角。

均质各向同性无限含水层中K为渗透系数;a=K/μs为含水层压力传导系数;在线汇Lw的作用下，P点的降深为

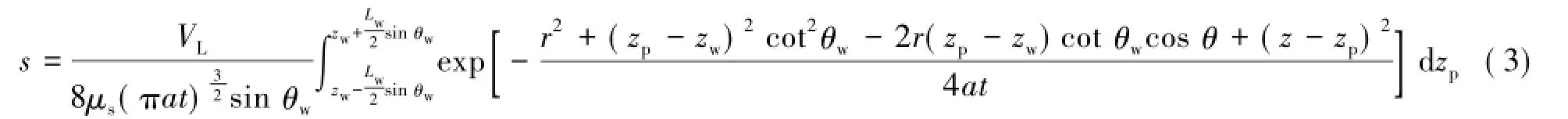
对各向异性无限含水层，设α=Krr/Kzz，则P点的降深为

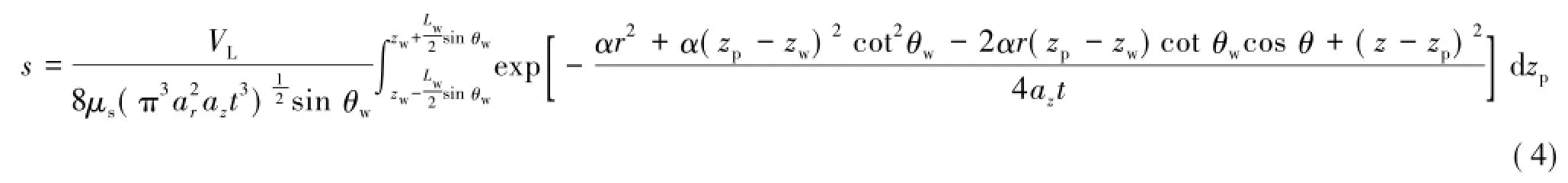
1.4有限空间连续线汇

有限空间中，在一连续强度为Q的线汇作用下，任意点的降深为s。那么，在τ时刻，在瞬时强度为Qdτ的线汇作用下，观测点则有ds的反映。对τ从0至t积分，可以得到在任意点连续疏放水强度QL的线汇作用下t时间的降深。对于顶底板隔水的各向同性水平无限含水层:

在均质各向异性有限含水层中P点的降深为

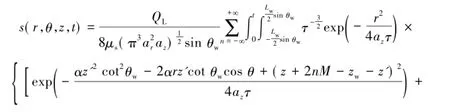
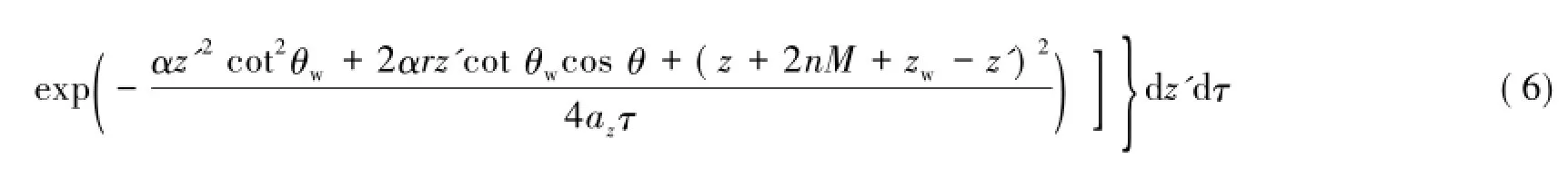
式(6)即为顶底板隔水的含水层中，长度为Lw，与水平方向夹角为θw的倾斜连续线汇的解析解表达式。将式(6)转换成求直角坐标的形式:

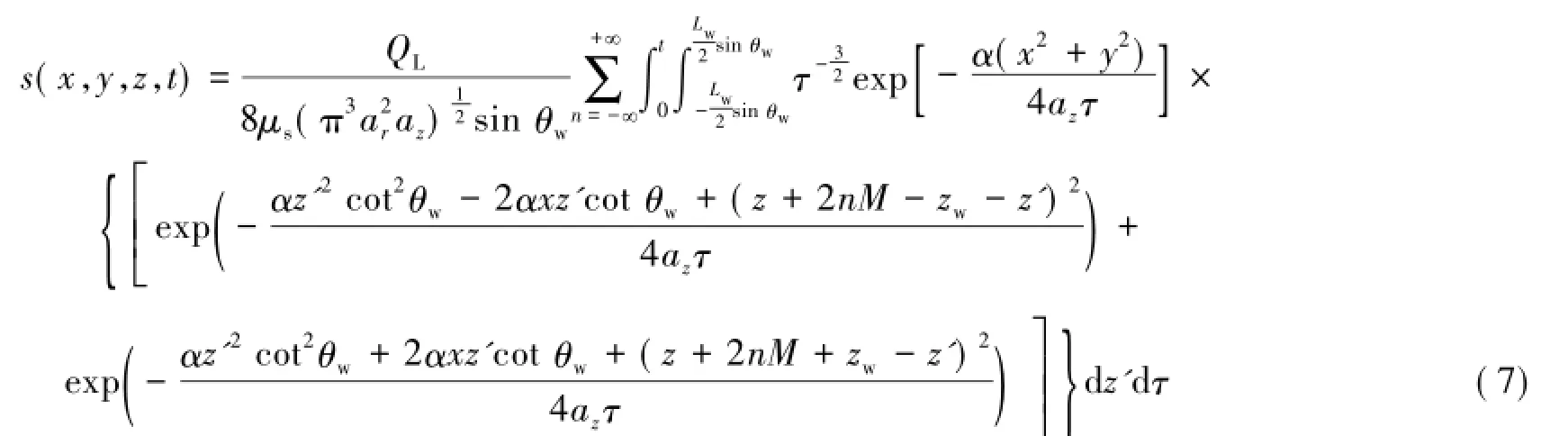
假设倾斜钻孔透水段中点在坐标系中的坐标为(j，k)，钻孔钻进方向与坐标系x方向的夹角为γ，则式(7)在该坐标系中的表达式为

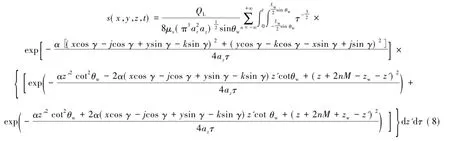
根据井群干扰原理多个疏放水孔在同一点产生的降深为各个疏放水孔单独引起降深的总和，即

通过计算每个钻孔在观测点的降深，并将其叠加，即将式(8)代入式(9)，就可以求得观测点的最终降深。

1.5线汇垂直与水平面

若线汇垂直于水平面，即θw=90°时，则式(5)可转化为

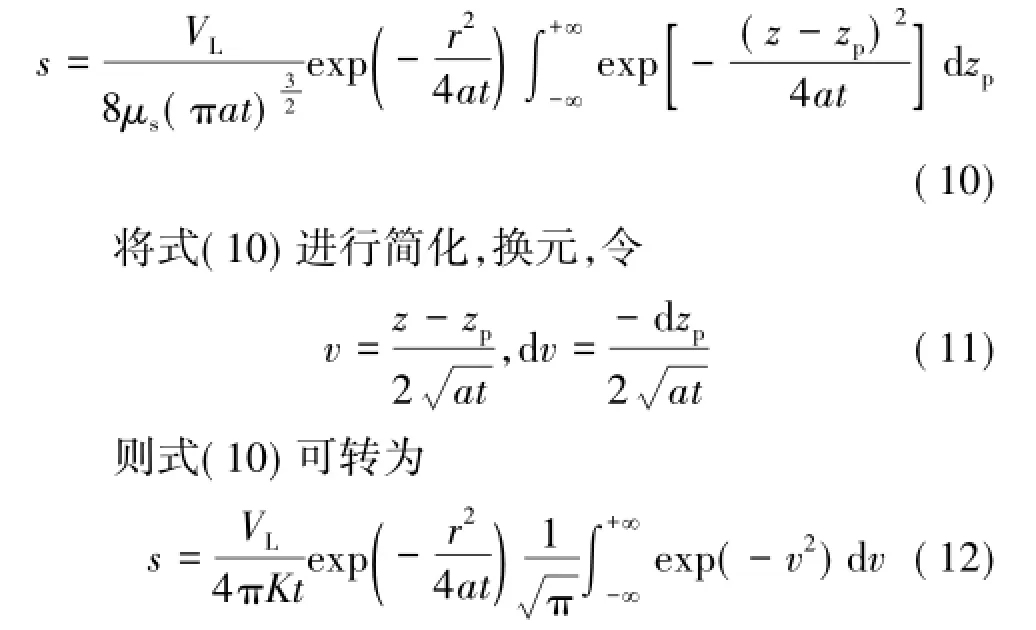
当含水层厚度为M时，线汇贯穿整个含水层，其强度为V。因此，厚度为M的承压含水层，平面瞬时点汇的方程为

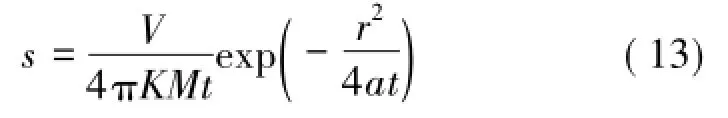
2　数值求解算例

为了更深入了解各个方程中的参数如何影响井流分布，本章选取了数个代表性参数并代入式(7)中，采用Matlab程序计算观测点的降深。

具体的求解过程:

(1)建立空间三维直角坐标系，以x，y，z对应水平方向及纵坐标，其中钻孔中点在z=0平面的投影作为坐标原点，钻孔钻进方向作为x轴正方向;

(2)选择特定水文地质参数、钻孔参数、时间及水量参数代入方程计算;

(3)计算观测点降深随时间变化的曲线，并对比不同观测点降深随时间变化的曲线;

(4)计算并对比不同观测位置，倾斜钻孔疏放水对观测点降深的影响。

2.1理想模型参数

图4反映了一个在承压含水层中进行疏放水的倾斜钻孔。为了讨论式(7)中各个参数对降深的影响，本节中考虑不同含水层参数、不同钻孔形态下的情形，并将承压含水层内水流假设为三维流。渗透系数的选取参考了砂岩含水层经验渗透系数。倾斜钻孔假定为透水段穿过整个含水层的完整井，当钻孔倾角变化时也将改变钻孔长度。其他参数的选取参考了陕北某矿工作面疏放水钻孔参数。

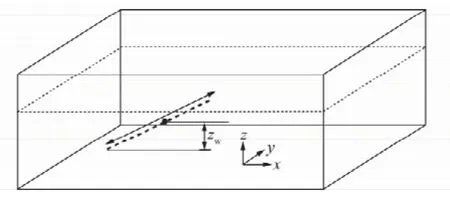
图4　倾斜钻孔顶板疏放水示意Fig.4　Schematic slant drilling roof water drainage

为方便讨论，疏放水时间为100 min，疏放水量为1.167 m3/min。

文化身份理论的代表人物是Collier和Thomas，该理论主要探讨的问题是在跨文化交往中个体应当如何处理文化身份。文化身份理论认为，交际双方在跨文化交际的过程中是拥有多元文化身份的个体；跨文化交际是一个永无止境的过程，人们在和其他人交流时，发展多元身份并对其进行管理（Collier&Thomas，1988）[4]。该理论有一个重要的命题，即文化身份越是自认定，在与其他身份相比时，它们的位置就越重要。该理论把跨文化交际和文化认同紧密联系起来，认为跨文化交际的前提和重要标识是交际双方对各自文化的认同。文化身份理论强调了在跨文化交际中，个体对母语文化认同的重要性。

与观测点相关的参数有3个，即观测的x，y，z坐标。观测点P的坐标见表1。

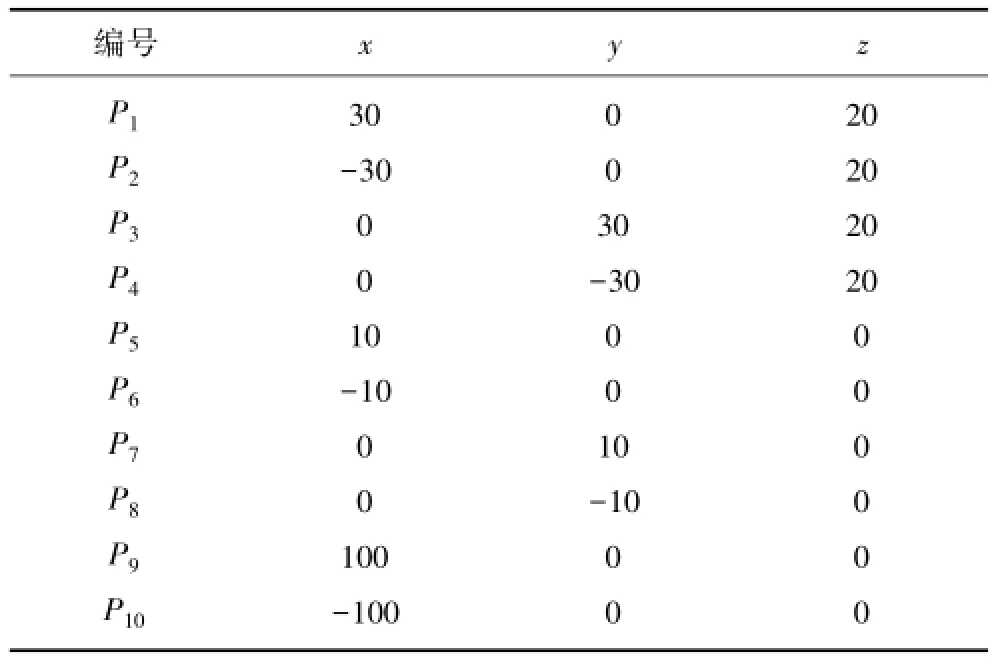
表1　观测点坐标取值Table 1　Observation point coordinate values　m

与钻孔形态有关的参数有3个:zw，θw，Lw。钻孔长度 Lw反映了钻孔在含水层中的长度，取值44.18 m，当钻孔穿过整个含水层时成为完整井，钻孔中点高度zw位于xy轴0点处，zw取值为20 m。θw反映钻孔与含水层之间的夹角，角度的变化将影响s的大小、降深等值线的形态，θw取值为65°。

与承压含水层有关的参数有4个:含水层厚度M，取值为40 m;渗透系数K，取值为0.000 125 m/min;垂向压力传导系数和水平压力传导系数比值α，取值为1;给水度μs，取值为0.000 008。

2.2降落漏斗形态计算

描述垂直钻孔疏放水时降深与时间关系的泰斯井流计算方程为二维流方程。求解泰斯井流计算方程所绘制观测点的s－t曲线仅与观测点与钻孔的水平距离有关。但倾斜钻孔井流计算方程所求解的是三维空间中各观测点的降深分布，求解倾斜钻孔井流计算方程所绘制的s－t曲线与观测点在三维空间中的位置有关。P3，P4观测点以x=0平面，即倾斜钻孔所在垂直平面为对称平面，相互对称。此时2个观测点的s－t曲线完全相同。P1，P2点虽然距离钻孔中心的距离与P3，P4点相同，但P1，P2点与P3，P4点的s－t曲线并不相同。

为了进一步了解倾斜钻孔定流量疏放水在不同观测点引起的水头降深的形态，选取三维空间中4个观测点，计算当t由0～4 320 min时各点的降深。观测点的坐标为:P5，P6，P7，P8计算结果如图5所示。P5，P6，P7，P8观测点与坐标轴原点的距离完全相同。

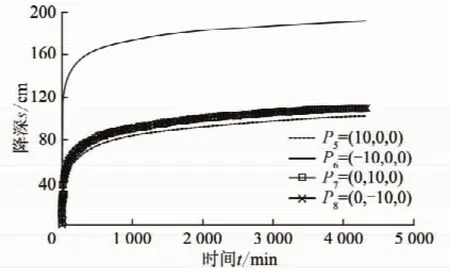
图5　不同观测点降深－时间的对比Fig.5　Different observation points drawdown-time comparison chart

由图5可以看出:以x=0平面，即倾斜钻孔所在垂直平面为对称平面，相互对称的两个观测点P7，P8的s－t曲线形状完全相同。以y=0平面，相互对称的两个观测点P5，P6的s－t曲线形状却完全不同，它们与P7，P8的s－t曲线形状也完全不同。

P5，P6虽然与坐标轴0点距离相同，但P6点降深明显大于P5点，这与倾斜钻孔的倾斜特点有关。对于任意2个观测点，只有当其坐标满足与钻孔距离的积分和相同时其s－t曲线形状才能完全相同。

为了了解含水层同一水平面内各观测点固定时刻的降落漏斗形态，计算t=4 320 min时，z=0，y=0线上－60 m至60 m的区域降深。以x轴为横坐标，降深s为纵坐标绘制图6，如图6所示降深曲线为一个不对称的漏斗形状，降深最大值位于x=－9 m点附近，这证明在该点处，观测点与疏放水钻孔上各点距离的平方和相对其他各观测点是最小的。

选取钻孔钻进方向沿y=0面做剖面图，计算x=－40 m至x=40 m，z=0至z=40 m区域内在t= 4 320 min时的降深，如图7所示。图7中颜色深浅代表该点降深的大小，由图7可以看出，在y=0剖面上，靠近钻孔的区域降深最大。假设初始水头相等，y=0剖面上地下水流速矢量图如图8所示。

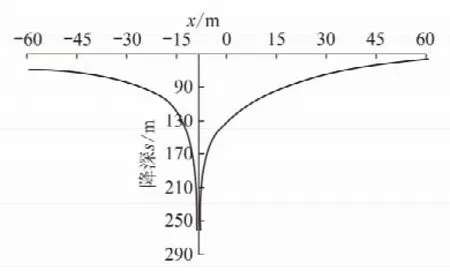
图6　x轴上降落漏斗形态示意Fig.6　x-axis cone of depression

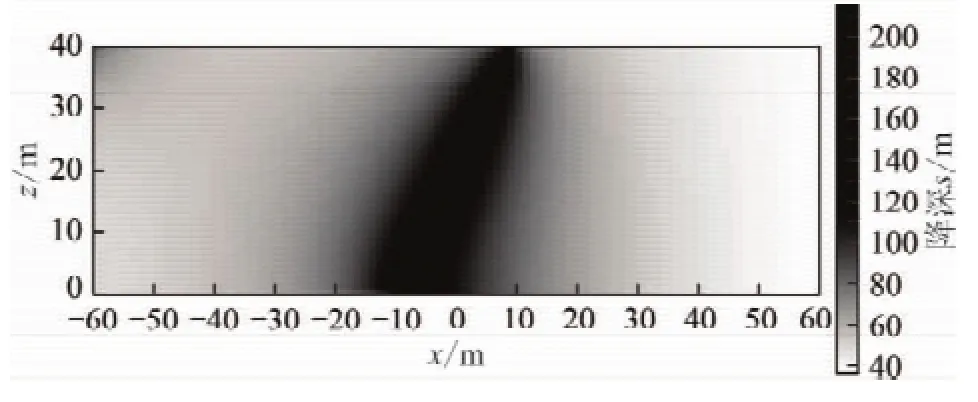
图7　y=0面计算区域降深灰度图Fig.7　y=0 calculate surface area grayscale drawdown

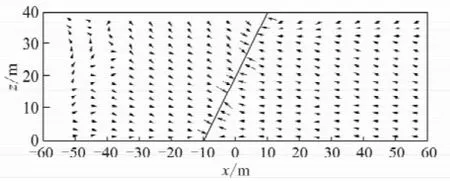
图8　y=0面计算区地下水流速矢量Fig.8　y=0 surface groundwater velocity vector calculation

由图7，8可以看出，在倾斜钻孔定流量疏放水的情况下，在剖面上降深自钻孔向外逐渐减小，地下水集中向钻孔区域流动。

为研究降深在水平方向的分布，选取z=10 m时x=－60 m至x=60 m，y=－60 m至y=60 m的平面，计算降深的分布情况，如图9所示。

由图9可以看出，在z=10 m平面上最靠近倾斜孔与平面交点处的降深最低，在平面上地下水呈现出降落漏斗的形态，等降深曲面的形状近似为椭圆形。

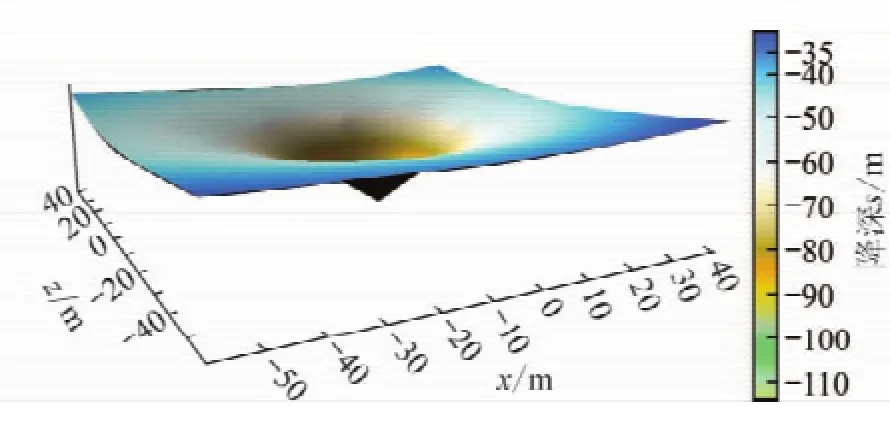
图9　z=10 m平面计算区地下水降深三维示意Fig.9　Three-dimensional schematic diagram of groundwater drawdown z=10 m flat calculate area

3　倾斜钻孔多孔叠加疏放水预测

3.1研究区背景

陕北某矿31101工作面是该矿井首采工作面，工作面回采3－1煤层，属于侏罗系延安组地层。31101工作面回采后，导水裂缝带高度将达到3－1煤顶板的侏罗系直罗组砂岩裂隙含水层。为了保证工作面安全回采，计划对31101工作面顶板施工倾斜疏放水钻孔对含水层进行提前疏放。本节应用上节推导的解析解对钻孔井流进行了计算，为疏放水钻孔方案验证，确定疏放水时间提供了依据。

3.2倾斜钻孔多孔叠加疏放水工程设计

矿方以前期勘探资料为基础，对整个工作面进行了疏放水钻探工程施工。钻孔参数及位置详见表2。

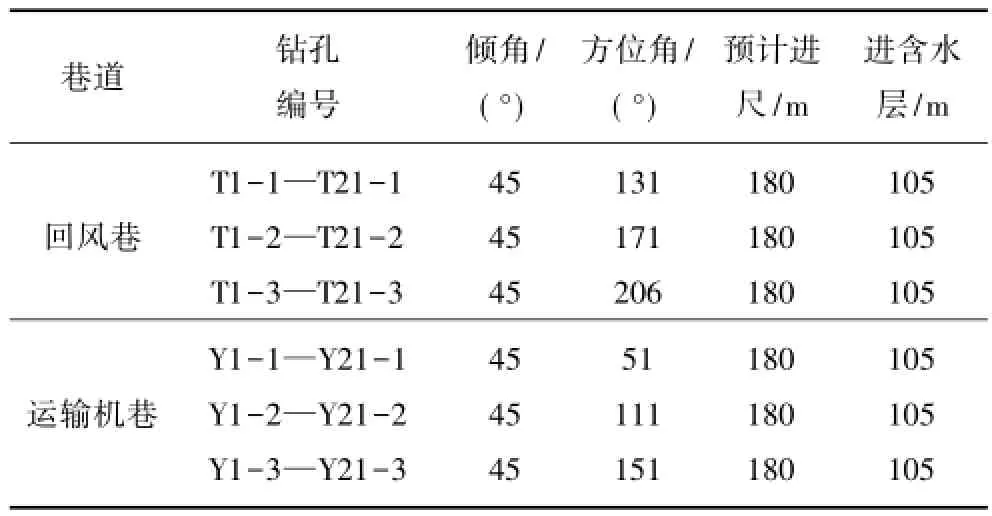
表2　31101工作面井下探放水钻孔参数Table 2　Parameters of slanted boreholes in 31101 work face

钻孔布置如图10所示。图中绿色线条围成的矩形区域为工作面范围，蓝色线条为施工的疏放水钻孔。工作面内共设计布置疏放水钻孔总数为126个，钻孔仰角均为45°，孔深为180 m。

3.3工作面疏放水预测计算

1.4节中推导的方程中的二重积分十分复杂，直接求解非常困难，选用数值法进行计算是更为可行的方法。本节采用Matlab编程，将工作面内钻孔参数及含水层参数代入方程数值求解了式(9)，含水层参数:厚度M为120 m;渗透系数K为0.18 m/d;纵向、横向渗透系数比 α为1;μs为0.000 008。得到了31101工作面顶板z=0平面内各点的降深，并将所求得结果绘制了降深等值线图。计算得到钻孔已定流量抽水3 d后31101工作面内地下水等降深值，如图10所示。

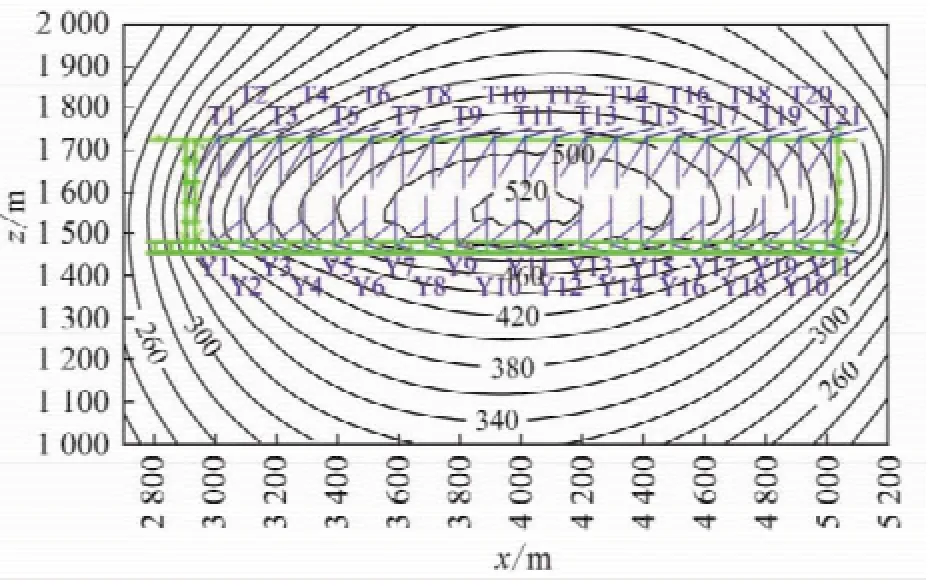
图10　31101工作面钻孔疏放水降深等值线Fig.10　31101 work face drilling water drainage drawdown contour map

由图10可知，31101工作面内疏放水钻孔全部按计划进行定流量疏放3 d后工作面内顶板直罗组含水层水位降深最大将达到500 m，满足了工作面顶板疏放水的要求。

按照设计疏放3 d后总疏放水量为82万m3，在陕北某矿矿井工作面实际施工过程中，总疏放水量约为78万m3，计算水量与实际疏放水量接近。

4　结　　语

(1)倾斜钻孔井流计算方程所求解的是三维空间中各观测点的降深分布，求解倾斜钻孔井流计算方程所绘制的s－t曲线与观测点在三维空间中的位置有关。

(2)降深曲线为一个不对称的漏斗形状，降深最大值靠近钻孔所在位置。观测点与疏放水钻孔上各点距离的平方和相对其他各观测点是最小的。在y= 0 m剖面上，靠近钻孔的区域降深最大。在倾斜钻孔定流量疏放水的情况下，在剖面上降深自钻孔向外逐渐减小，地下水集中向钻孔区域流动。观测点越靠近倾斜孔与平面交点处其降深越低，在平面上地下水呈现出降落漏斗的形态。

(3)通过对现场试验的研究结合倾斜钻孔井流计算方程，进一步验证了倾斜钻孔井流计算方程适用于煤矿疏放水的实际工作。

参考文献:

［1］ 国家安全生产监督管理总局．煤矿防治水规定［M］．北京:煤炭工业出版社，2009．

［2］ 国家安全生产监督管理总局．煤矿安全规程［M］．北京:煤炭工业出版社，2011．

［3］王旭升，万力．地下水运动方程［M］．北京:地质出版社，2009．

［4］ 孙讷正．地下水流的数学模型和数值方法［M］．北京:地质出版社，1981．

［5］ 李竞生，姚磊华．含水层参数识别方法［M］．北京:地质出版社，2003．

［6］薛禹群，吴吉春．地下水动力学［M］．北京:地质出版社，2010．

［7］薛禹群，谢春红．地下水数值模拟［M］．北京:科学出版社，2007．

［8］ 陈崇希．地下水流数值模拟理论方法即模型设计［M］．北京:地质出版社，2013．

［9］ 詹红兵，万军伟．水资源和环境工程中水平井研究简介［J］．地球科学:中国地质大学报，2003，28(5):511－517．Zhan Hongbing，Wan Junwei．Horizontal wells in water resources and environmental engineering［J］．Earth Science(Journal of China University of Geosciences)2003，28(5):511－517．

［10］CincoLey．Unsteady-state pressure distribution created by a directionally drilled well［J］．Journal of Petroleum Technology，1975，27(11):1392－1400．

中图分类号:TD745

文献标志码:A

文章编号:0253－9993(2016)06－1517－07

收稿日期:2015－06－23修回日期:2015－12－08责任编辑:韩晋平

基金项目:国家自然科学基金资助项目(41302214);陕西省自然科学基础研究资助项目(2014JM2－5064);中煤科工集团有限公司面上基金资助项目(2014MS002)

作者简介:陈实(1983—)，男，湖北孝感人，助理研究员。Tel:029－87862248，E－mail:38785899@qq．com。通讯作者:董书宁(1961—)，男，陕西蓝田人，研究员。Tel:029－81778066，E－mail:dsn_61@hotmail．com

Analytical solution for slanted well in the roof of coal mine working face

CHEN Shi1，2，DONG Shu-ning1，2，LI Jing-sheng1，WANG Hao1，2，YANG Jian1，2
(1．Xi’an Research Institute Co．Ltd．，of China Coal Technology＆Engineering Group Corp，Xi’an710054，China;2．Shaanxi Key Laboratory of Coalmine Water Hazard Control，Xi’an710077，China)

Abstract:Water-inrush from roof is one of the most harmful hazards to coal mine construction and production．The technologies of slanted drilling and drainage have been widely used in the field of coal mine water prevention and treatment，especially in preventing and controlling the water-inrush from roof．Based on the theory of point source space，this paper derived a calculation method of the well flow caused by slanted borehole in infinite horizon confined aquifer．Superposition of infinite horizontal porous confined aquifer complete slanted bore-hole flow calculation equation has been verified．A set of analysis，simulation and forecast of the coal mine roof slanted borehole drainage theory and method of water was formed．Calculation equation for slanted borehole laid a good foundation to the design of the coal mining face water discharge．

Key words:slanted borehole;roof water gush in coal mines;well flow;coal mine working;analytical solution