无外部扰动的均直巷道风速和风压测不准机理实验研究

刘　剑，李雪冰，宋　莹，高　科，邓立军

(1．辽宁工程技术大学安全科学与工程学院，辽宁阜新　123000;2．矿山热动力灾害与防治教育部重点实验室，辽宁阜新　123000)



无外部扰动的均直巷道风速和风压测不准机理实验研究

刘剑1，2，李雪冰1，2，宋莹1，2，高科1，2，邓立军1，2

(1．辽宁工程技术大学安全科学与工程学院，辽宁阜新123000;2．矿山热动力灾害与防治教育部重点实验室，辽宁阜新123000)

摘要:井下风速和风压的波动通常被认为是由外部扰动引起的，但是，即使在实验室条件下对可能的外部扰动给予充分的控制，风速和风压的示值仍始终呈现不规则的波动，即测不准现象。对此，从湍流角度出发对这一现象的产生机理进行了研究。利用激光多普勒测速仪和数字式微压差计测量了中低风速下巷道模型风速和静压的时间序列。结果显示，在无外部扰动的均直光滑巷道内，风速和压力依然存在波动，其大小和方向均发生剧烈变化，总体上呈现出在一平均值附近的随机脉动;当平均风速和平均压力分别为2．57 m/s和17．1 Pa时，风速和压力的最大脉动幅度分别达到了1．19 m/s和4．9 Pa。风速和压力的脉动信号服从正态分布，平均脉动幅度分别与速度和速度平方成正比，但测不准现象与风速大小关系不大仅受湍流强度影响。实验表明，即使在无外部扰动的条件下，井下风速和风压也是测不准的，测不准的本质是井下湍流随机脉动特性所致。而湍流具有规则的统计平均结果，是可以精准测量的。为了获得井下风流的精准参数，风速及风压等测试仪器应基于湍流的统计平均特性来设计研发。

关键词:矿井湍流;测不准;脉动;扰动;风速;风压

刘剑，李雪冰，宋莹，等．无外部扰动的均直巷道风速和风压测不准机理实验研究［J］．煤炭学报，2016，41(6):1447－1453．doi:10．13225/j．cnki．jccs．2015．1347

Liu Jian，Li Xuebing，Song Ying，et al．Experiment study on uncertainty mechanism of mine air velocity and pressure with non-external disturbances［J］．Journal of China Coal Society，2016，41(6):1447－1453．doi:10．13225/j．cnki．jccs．2015．1347

矿井通风参数众多，但最重要的是风速和风压，掌握了这2个基本参数就可以导出其他参数(如风阻、功率等)，然而实现对两参数的精准测量却并非易事。笔者所在课题组通过对国内近200个煤矿及非煤矿井的通风阻力测试，发现测量风速时不管是采用机械风表、电子风表还是基于各种感知原理的风速传感器，仪表示值均呈现不同程度的波动。同样在测压时，无论采用气压计、压差计，或是基于各种感压原理的传感器，压力示值也呈现不同程度的波动，有时波动幅度甚至大于测试真值。风速和压力的这种波动性在国内外相关文献中也均有描述［1－4］，有学者称其为测不准现象。学术界普遍认为风速和风压的波动源于井下各种扰动影响［5－6］，如风门开启、罐笼提升、溜煤眼放空、人员活动、矿车运行、爆破气流、风机运转等。然而，笔者发现，即使在实验条件下对可能的扰动因素给予充分控制，风速和压力的示值依然存在波动。为了探究这一现象的成因，本文设计制作了无外部扰动的通风巷道模型，利用激光多普勒测速仪(LDA)和数字式微压计采集巷道模型内风流速度和相对静压的时间序列并进行统计分析，试图从湍流角度出发对井下风速和压力的测不准现象给予更为科学的解释。

1　实验装置和测量方法

(1)无外部扰动实验模型设计。

井下风流的扰动因素众多，总体可分为两类:一类是动态扰动，如风门开启、罐笼提升、溜煤眼放空、人员活动、矿车运行、爆破气流、风机运转等;另一类为静态扰动，包括巷道走向、断面尺寸、壁面粗糙度等流动环境的变化。两类扰动会引起风流的非定常流动或局部大尺度涡旋的产生，从而导致测不准现象，这是学者普遍接受的观点。本文设计的无外部扰动实验模型力求消除上述两类扰动因素。实验装置如图1所示，其中巷道模型为均直光滑的矩形管道，与原型几何尺寸之比为1∶10，模型材料为5 mm厚有机玻璃板，截面尺寸为0.2 m×0.2 m，长为12 m。为消除风机的不均匀运转对风流造成的扰动，利用空气压缩机和储气罐组成的恒量供风装置提供风源，并在巷道模型的入口和出口均安置整流格栅。通过调节入口阀门开度改变实验风速，测量断面距离入风口8 m，经LDA全断面风速测量验证，此处已呈稳定充分发展的湍流状态。

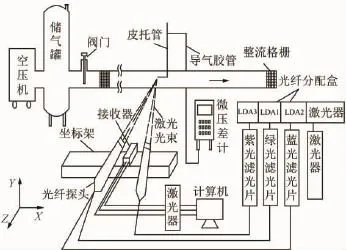
图1 实验装置Fig.1　Experiment setup

(2)测速系统。

采用DANTEC公司生产的后散射型三维LDA进行测量。测量时，由亚离子激光器产生的激光束经分光器分成蓝(LDA2)、绿(LDA1)、紫(LDA3)3对6束单色光，分别测量X(流向)，Y(垂向)，Z(横向)3个方向的速度分量;光束经传输光纤送入发射探头，聚集在一点形成测量体;事先布撒在流场中的示踪粒子跟随气流通过测量体时产生的散射光信号被光电接受器内的光电转换器件转化为电信号后传送到信号处理器和主控计算机进行分析处理最终得到该点的三维速度分量［7－8］，测速精度为0.1%。实验中示踪粒子采用祭祀香燃烧产生的烟气，粒径小于2 μm，满足跟随性要求，测量时根据接收信号的变化调节烟气释放量和滤波器带宽。

(3)测压系统。

利用L型标准皮托管感受测点处的相对静压变化，经导气胶管传递至M7000型数显微压差计进行采集，微压差计量程为±45 Pa，测量精度0.25%FS。

2　实验结果及分析

2.1瞬时速度时间序列特征

选取巷道断面中心点风速的采样数据进行分析。图2是平均风速V =2.57 m/s、雷诺数Re=3.4×104时断面中心测点三维瞬时速度分量在10 s内的采样时间序列。可以看出，风流质点的速度时间序列极不规则，X，Y和Z向的瞬时速度分量均随时间发生极不规则的剧烈变化，总体表现为在一平均值附近的随机涨落。采样数据的统计结果见表1。

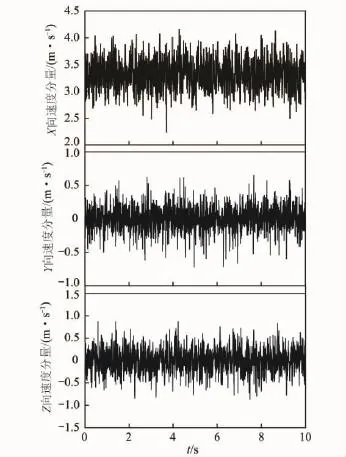
图2　各向速度分量的时间序列Fig.2　Time-series data of three velocity components

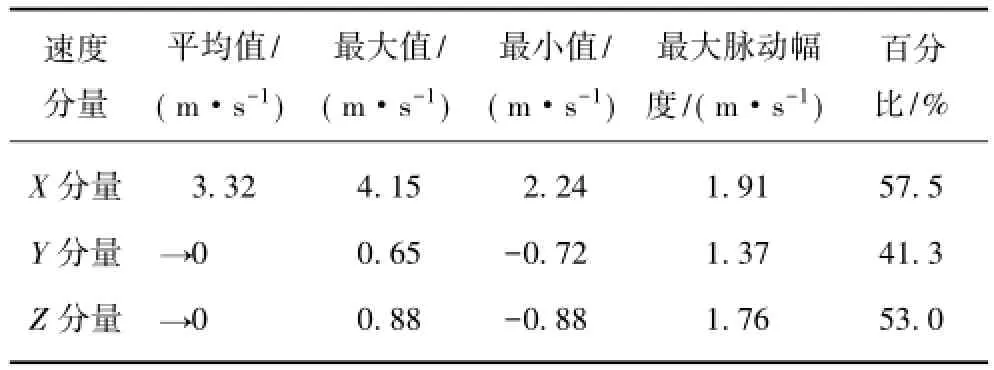
表1　速度采样数据的统计结果Table 1　Statistical results of the velocity sampled data

测试结果表明，即使在理想的均直光滑巷道内，瞬时速度仍呈现波动状态，不仅表现在速度大小的随机脉动其方向也在随时发生变化，这种不规则的随机波动称为湍流脉动［9－10］。Y，Z方向速度分量的统计平均值趋于0，表示主流方向为X方向，与实际宏观流动相符，这表明湍流脉动虽然具有不规则性和随机性，但它具有规则的统计平均结果。而井下无论何种原理的风速传感器，所感受的只是瞬时风速，未经合理尺度上的统计平均处理，因而表现为测不准现象。为研究湍流脉动速度的统计分布规律，根据概率平均收敛的采样条件(另文介绍)取X向速度分量2 000个样本点绘制出风速频数分布直方图并附加正态概率密度曲线，如图3所示。

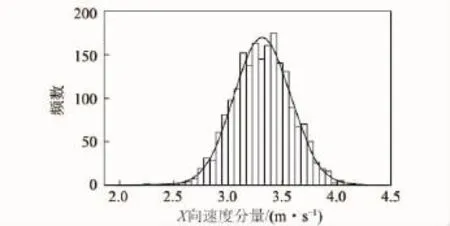
图3　风速频数分布直方图Fig.3　Frequency histogram of velocity sampled data

由图3可以看出，风流速度脉动采样数据接近正态分布。利用SPSS统计分析软件的“P－P图”功能进行正态分布检验，分箱检验结果如图4所示。其中，横坐标为数据样本的累积概率，纵坐标为正态分布计算的相应累积概率。风速采样数据点呈围绕第1象限对角线的直线，表明这些采样数据服从正态分布。利用SPSS的“K－S”功能对该组数据做进一步的正态分布检验，结果表明，双侧渐进显著性取值为0.79，大于拒绝临界值0.05，因此接受正态分布假设;在5%的显著性水平上，采样风速均值的置信区间为［3.30，3.34］，包括3.32 m/s且均值为3.32 m/s成立的概率为99.5%。对整个断面内的测量点及对应的Y向和Z向速度采样数据做相同的统计分析，其检验结果亦满足正态分布要求，因此，巷道内湍流速度脉动服从正态分布。

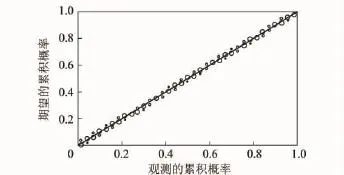
图4　风速正态分布检验Fig.4　Normality test of velocity sampled data

2.2瞬时压力时间序列特征

湍流速度和压力的关系可由N－S运动方程描述。

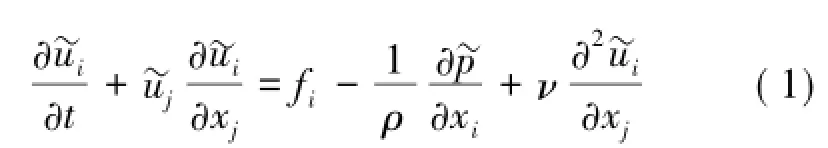
其中，u槇i，u槇j为i，j方向瞬时速度分量，m/s;p槇为瞬时压力，Pa;ρ为空气密度，kg/m3;ν为流体的运动黏性系数，m2/s;fi为i方向的体积力。令 u槇i=＜ui＞+u'i，p槇=＜p＞+p'代入式(1)得到时均运动的Renolds方程，与式(1)相减可以得到脉动速度u'和脉动压力p'关系方程为

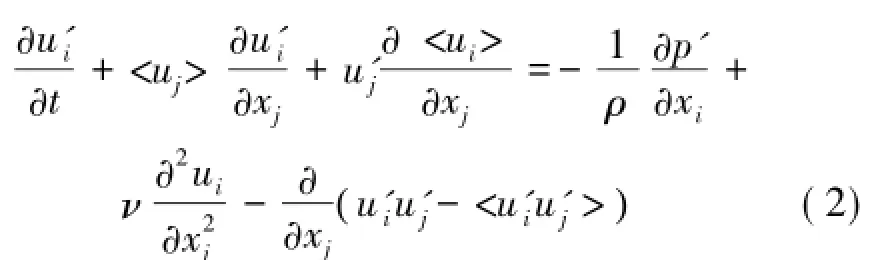
其中，＜ui＞，＜p＞分别为速度和压力的时均值。由N－S方程可直观看出，当流动速度发生变化时，压力也随之改变，速度与压力的变化是同时存在并具有某种内在联系。由式(2)可知，压力脉动除了受速度脉动影响外还与耗散有关，其相互作用关系十分复杂，无法获得压力脉动与速度脉动关系的解析表达，因而压力脉动的相关特征尚依赖实验观测。

图5为平均速度为2.57 m/s、Re=3.4×104时，断面中心测点相对静压在300 s内的采样时间序列。可以看出，压力瞬时值与速度类似，在一平均值附近随机涨落呈不规则的脉动状态，由于目前尚没有与激光多普勒测速仪类似的高频响测压仪器，因而所呈现的压力脉动较速度脉动迟缓。经统计分析，该组数据的最大值pmax=19.6 Pa，最小值pmin=14.7 Pa，平均值=17.1 Pa，最大脉动幅度为4.9 Pa。实验表明，在无外部扰动影响下，由于湍流脉动作用，瞬时压力仍表现出较大幅度的波动，这一波动导致测量结果失准。

图5　湍流压力脉动时间序列Fig.5　Time-series data of pressure fluctuations in turbulents

为研究湍流压力脉动分布规律，对该组数据绘制出频数分布直方图如图6所示。图7是利用“P－P图”命令对该组数据的正态分布的检验结果。由图7可以看出，压力采样数据点呈围绕第1象限对角线的直线，表明这些采样数据服从正态分布。进一步利用“K－S”功能对该组数据正态分布的检验结果表明，双侧渐进显著性取值为0.98，大于拒绝临界值0.05，接受正态分布假设;在5%的显著性水平上，该组数据均值的置信区间为［16.9，17.2］，包括平均值17.1 Pa，且均值为17.1 Pa的概率为99.2%。因此，巷道内湍流压力脉动服从正态分布。

图6　压力频数分布直方图Fig.6　Frequency histogram of pressure sampled data

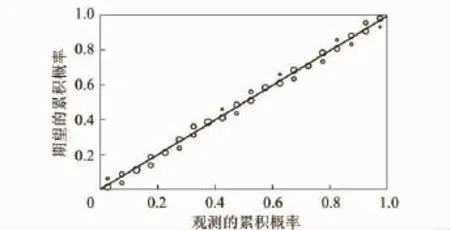
图7　压力正态分布检验Fig.7　Normality test of pressure sampled data

2.3风速大小对湍流脉动的影响

湍流速度脉动相关的参数中，最常用的是标准差和湍流强度［11－12］。速度脉动标准差可以用来表征测试数据波动幅度的大小，标准差越大，平均脉动幅度越大，测量结果的绝对误差越大。而湍流强度(本文指主流X方向的湍流强度I=δ/V ×100%，δ为湍流平均脉动幅度)可用于表示不同测试风速下，采样数据的离散程度，数据离散程度越大测量结果失准概率越大，因此湍流强度可以做为测不准现象的定量表征。图8给出了煤矿井下常见风速范围内的10种风速下，采样数据的标准差和湍流强度的变化趋势。由图8(a)可以看出，随平均风速增大，测点速度的平均脉动幅度近似呈线性增加，即风速越大，湍流平均脉动幅度越大;由图8(b)可以看出，随平均风速增大，测点处的湍流强度(即采样离散程度)有减小趋势，但减幅不大，当V由0.58 m/s增至5.2 m/s时，I值由5.86%增至4.61%，减幅仅为1.25%。综上可知，测试风速越大，湍流平均脉动幅度越大，可引起的宏观波动尺度越大，而湍流强度变化不大，这表明风速测不准现象与风速大小关系不大;从测试误差的角度来看，随风速增大，测试的绝对误差不断增加，而相对误差近似不变。

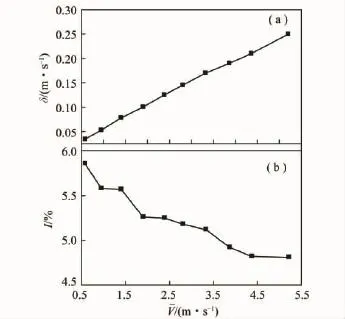
图8　风速大小对湍流脉动的影响Fig.8　Effect of velocity on turbulence fluctuations

3　现场测试

现场测试在我校实验矿井内进行(图9)，可避免实际井下各种扰动源影响，通过调节风门a，b改变测试风速。实验段为一段长为200 m的均直矩形巷道，断面尺寸为3 m(宽)×2.5 m(高);测试断面距风流入口150 m，测点位于断面轴心;利用L型标准皮托管感应测点处的速压变化，并转换为数字信号显示于微压差计电子屏上。每种风速下手工记录200组速压数据(一般需要3～5 min)，按照式(3)转换为瞬时风速值V。

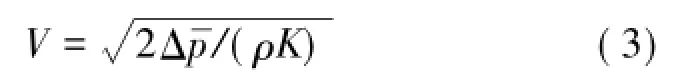
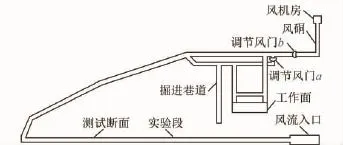
图9　实验矿井平面示意Fig.9　Schematic plan view of experimental mine

实验采集了5种风速条件下的瞬时风速值，经检验，现场采集的瞬时风速仍服从正态分布。利用统计平均方法获得不同风速下的平均脉动幅度和湍流强度，并与实验室的测试结果进行对比，如图10所示。从图10来看，随时均风速增大，湍流平均脉动幅度和湍流强度的实验结果与现场测试结果具有一致的变化趋势，表明利用小断面巷道模型获得的定性结论在实际巷道中仍然适用。从量化结果来看，在相同风速条件下，现场测得的湍流平均脉动幅度和湍流强度均略小于实验测试结果，这是由测试巷道断面尺寸的变化而引起的。因此认为，相同风速下，巷道断面越小，湍流脉动越激烈，但断面尺寸对湍流脉动的影响十分微弱即测不准现象与巷道断面尺寸的关系亦不大，表明即使在无外部扰动的均直巷道中仍然存在十分激烈的湍流脉动。

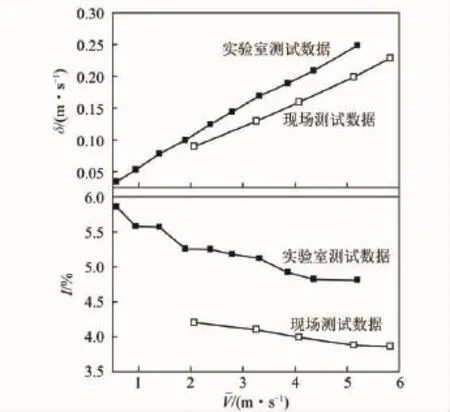
图10　实验结果与现场测试结果对比Fig.10　Experimental results compared with on-the-spost test

4　阻力测定中测压仪表示值波动的近似解释

对于通风阻力测定中速度和压力的宏观波动关系，本文试图从空间点压能的角度做近似理解，其目的仅是为了解释阻力测定中压力测试值波动的现象。风流内任一点的点压由静压、速压、位压构成，伯努利方程指出

式中，h为压差计液面高度。

当风流视为不可压缩流动时位压保持不变，显然，流动速度增大时，静压减小，流速减小，静压增大。在湍流脉动作用下，不难理解气压计法测试矿井通风阻力时仪表示值的波动现象。

对于压差计法测试井巷风阻时，静压管管孔(皮托管静压孔)所感知的是当地点压能信息，由于流体质点在湍流脉动作用下会产生Y，Z方向的速度分量，导致静压孔中混入少量动压信息，因而皮托管的静压孔感受了部分速压，而全压孔感受的则不是全部速压，速压与静压在湍流脉动作用下不断转换，这一信息传递至倾斜压差计，使液面表现为不稳定的上下波动。由于湍流脉动属瞬态变化，皮托管感知的不同尺度的湍涡脉动信号，这些信号在导气胶管中以声速传递至压差计两端液面并产生一定时差，因此严格讲，倾斜压差计测阻法并非同步测量，其液面的宏观波动是大量湍流脉动信号在液面终端叠加和耗散的平均作用结果。根据实验结果和倾斜压差计法测阻原理，将湍流脉动与压力波动关系简化为如图11所示模型。

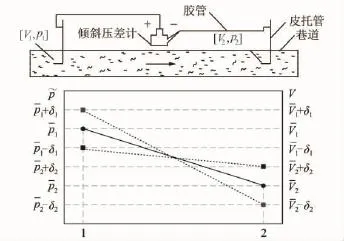
图11　速度与压力脉动关系简化模型Fig.11　Simplified model of relationship between velocity and pressure

对图11的解释如下:k(k=1，2)表示巷道阻力测定段的始末测点;Vk，pk为k点瞬时风速和瞬时压力;为k点平均流速和平均压力;σk，δk为k点速度和压力的平均脉动幅值。当k点风速为Vk时，压力为;当k点风速为+σk或－σk时，对应压力为－δk或+δk。

单位质量元流流体的能量方程为

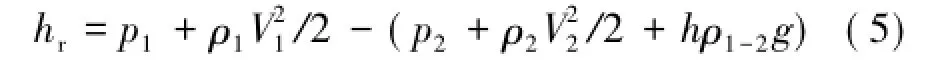
其中，hr为巷道断面1，2间的通风阻力，Pa;ρ1－2为两端面间巷道内的空气密度平均值，即(ρ1－ρ2)/2，kg/m3。利用倾斜压差计法测算巷道两断面间通风阻力时

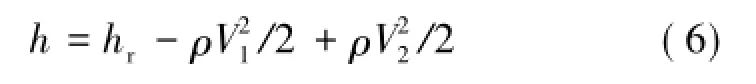
两断面间通风阻力为一定值，当V1=V1－δ1，V2=+δ2时，h=hmax;当V1=+δ1，V2=+δ2时，h=hmin由湍流速度脉动引起的压差计测试数据的波动幅值为

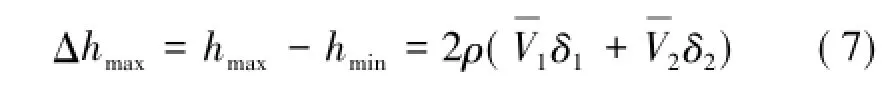
当V1=V2且两断面间湍流强度不变时，Δhmax= 2ρI，因此由两断面间湍流速度脉动引起的压差计测试数据的波动范围，Δh∈［0，2ρI，可以看出，测压仪表的平均波动幅度与当地湍流强度及平均风速的平方成正比，而h～，测试相对误差ε=Δh/h，则ε与I成正比。从测试误差来看，压力测不准现象与风速大小无关，仅受湍流强度影响，这与风速的测不准现象具有一致性。

5　结　　论

(1)即使在无外部扰动的理想均直巷道内，风速和风压仍然存在波动，亦即测不准现象是绝对存在的而并非单纯由外部扰动决定，湍流随机脉动是风速和风压测不准现象的本质原因。

(2)风速和压力的湍流脉动均服从正态分布，且风速和压力的平均波动幅度分别与速度和速度的平方成正比，但测不准现象与风速大小关系不大，仅与湍流强度成正比。从测试误差来看，随风速增大，测试的绝对误差不断增加，而相对误差近似不变。

(3)通风参数在湍流脉动作用下呈现极不规则的变化，但它具有规则的统计平均结果，理论上可以实现精准测量。为了获得井下风流的精准参数，风速及压力测试仪器应基于湍流的统计平均特性来设计研发。

参考文献:

［1］范京道．矿井风量波动与漂移的溯源分析研究［D］．西安:西安科技大学，2013．Fan Jingdao．Study on the cause tracing of airflow fluctuation and drift in mine ventilation system［D］．Xi’an:Xi’an University of Science and Technology，2013．

［2］王德明．矿井通风阻力测定中的气压监测问题［J］．煤炭工程师，1992(5):18－20．Wang Deming．Pressure monitoring problem in the measurement of ventilation resistance［J］．Coal Engineer，1992(5):18－20．

［3］王树刚，刘宝勇，刘贵文．矿内空气非定常流动能量方程及在测阻中的应用［J］．矿业安全与环保，2001，28(1):28－30，64．Wang Shugang，Liu Baoyong，Liu Guiwen．Non-stationary flow energy equation for mine air and tis application in resistance measurement ［J］．Mining Safety＆Environmental Protection，2001，28(1):28－30，64．

［4］司俊鸿，陈开岩．基于Tikhonov正则化的矿井通风网络测风求阻法［J］．煤炭学报，2012，37(6):994－998．Si Junhong，Chen Kaiyan．Measuring airflow＆ evaluating resistance model of the mine ventilation network based on tikhonov regularization［J］．Journal of China Coal Society，2012，37(6):994－998．

［5］王树刚，王继仁，桂祥友．矿内空气非定常流动规律研究［J］．辽宁工程技术大学学报(自然科学版)，1998，17(4):337－342．Wang Shugang，Wang Jiren，Gui Xiangyou．A study of unsteady airflow laws in mine［J］．Journal of Liaoning Technical University(Natural Science)，1998，17(4):337－342．

［6］鲁义，钟万滋，盛真可．影响矿井通风阻力测定因素分析［J］．江西煤炭科技，2011(1):80－82．Lu Yi，Zhong Wanzi，Sheng Zhenke．Factor analysis of effect of survey of mine ventilation resistance［J］．Jiangxi Coal Science＆Technology，2011(1):80－82．

［7］张艳艳，巩轲，何淑芳，等激光多普勒测速技术进展［J］．激光与红外，2010，40(11):1157－1162．Zhang Yanyan，Gong Ke，He Shufang，et al．Progress in laser doppler velocity measurement techniques［J］．Laser＆ Infrared，2010，40(11):1157－1162．

［8］陈益萍．激光多普勒测速技术原理及其应用［J］．电子技术，2013(4):35－37．Chen Yiping．Principle of laser doppler velocimetry and its application［J］．Electronic Technology，2013(4):35－37．

［9］是勋刚．湍流［M］．天津:天津大学出版社，1994．

［10］张兆顺，崔桂香，许春晓．走近湍流［J］．力学与实践，2002，24(1):1－8．Zhang Zhaoshun，Cui Guixiang，Xu Chunxiao．Approaching to turbulence［J］．Mechanics in Engineering，2002，24(1):1－8．

［11］翟明，董秡，王希影，等．圆管湍流脉动与换热数值模拟［J］．中国电机工程学报，2009，29(20):85－91．Zhai Ming，Dong Peng，Wang Xiying，et al．Numerical simulation of turbulent pulsating flow and heat transer in tubes［J］．Proceedings of the CSEE，2009，29(20):85－91．

［12］周济福，张强，李家春．近壁湍流脉动的概率分布函数［J］．应用数学和力学，2005，26(10):1135－1142．Zhou Jifu，Zhang Qiang，Li Jiachun．Probability distribution function of near-wall turbulent velocity fluctuations［J］．Applied Mathematics and Mechanics，2005，26(10):1135－1142．

中图分类号:TD72

文献标志码:A

文章编号:0253－9993(2016)06－1447－07

收稿日期:2015－09－14修回日期:2016－01－15责任编辑:张晓宁

基金项目:国家自然科学基金资助项目(51574142);国家自然科学基金委员会与神华集团有限公司联合资助项目(51174265)

作者简介:刘剑(1961—)，男，内蒙古赤峰人，教授。E－mail:lj1961@vip．sina．com

Experimental study on uncertainty mechanism of mine airvelocity and pressure with non-external disturbance

LIU Jian1，2，LI Xue-bing1，2，SONG Ying1，2，GAO Ke1，2，DENG Li-jun1，2
(1．College of Safety Science and Engineering，Liaoning Technical University，Fuxin123000，China;2．Key Laboratory of Mine Thermodynamic Disasters and Control of Ministry of Education，Fuxin123000，China)

Abstract:Fluctuations of mine air velocity and pressure are generally considered to be caused by external disturbances．But even if external disturbances are fully controlled in a lab environment，the indicated values of velocity and pressure still present irregular fluctuations which is known as uncertainty phenomenon．Mechanism which causes the uncertainty phenomenon was studied from the turbulent theory．Time-series data of air velocity and static pressure in a tunnel model were measured by laser dopper anemometer(LDA)and digital differential manometer．The results show that the fluctuations still exist in both magnitude and direction，which generally present a random fluctuation around an average value．The maximum pulsating amplitude of air velocity and pressure reach 1．19 m/s and 4．9 Pa respectively when their average values are 2．57 m/s and 17．1 Pa respectively．Both velocity and pressure fluctuation signals followa normal distribution．Their average pulsating amplitudes are respectively proportional to velocity and its square，but the uncertainty phenomenon is only affected by turbulence intensity instead of velocity．Experiments show that mine air velocity and pressure are uncertainty even with non-external disturbances which is essentially caused by turbulence fluctuations．Yet，turbulence can be measured accurately because it has regular statistical average value．To get accurate parameters in the tunnel airflow the development of test instruments should be based on the statistical average value of turbulence．

Key words:mine turbulence;uncertainty;fluctuation;disturbance;air velocity;air pressure