横向简谐荷载作用下端锚黏结式锚杆黏结性试验研究
张哲诚,张向东,刘源浩,李庆文
(辽宁工程技术大学土木与交通学院,辽宁阜新 123000)
横向简谐荷载作用下端锚黏结式锚杆黏结性试验研究
张哲诚,张向东,刘源浩,李庆文
(辽宁工程技术大学土木与交通学院,辽宁阜新123000)
摘要:由于采动荷载和爆破荷载对已有支护锚杆产生影响,因此迫切需要研究锚杆在动荷载作用下的微观力学特性及黏结性变化。从工程实际出发,现场监测锚杆工作状态下轴力变化和爆破荷载作用下锚杆周边围岩振动信息,并开展探索性室内试验。通过室内试验获得锚杆在轴向荷载作用下横向固有频率振动后的振动强度与工作龄期耦合作用下锚杆黏结性衰减规律的拟合计算式。研制了横向简谐荷载作用下端锚黏结式锚杆模型试验装置,采用均匀设计方法,考虑锚杆长度和锚杆直径两个影响因素,通过动态监测系统获得了横向简谐荷载作用下锚杆应力沿锚杆长度的分布规律、锚杆应力分布与拉拔力的关系,以及剪切应力与位移的关系。最终采用大型有限差分软件FLAC3D,建立了锚杆与围岩相互作用的力学模型。
关键词:横向简谐荷载;锚杆固有频率;黏结性衰减;极限锚固力
张哲诚,张向东,刘源浩,等.横向简谐荷载作用下端锚黏结式锚杆黏结性试验研究[J].煤炭学报,2016,41(6):1407-1415.doi: 10.13225/j.cnki.jccs.2015.1277
Zhang Zhecheng,Zhang Xiangdong,Liu Yuanhao,et al.Experimental research of anchors bonding mechanical properties under transverse harmonic loads[J].Journal of China Coal Society,2016,41(6):1407-1415.doi:10.13225/j.cnki.jccs.2015.1277
煤炭资源在开采过程中,大量的使用锚杆进行支护,锚杆在工作的过程中常常受到爆破荷载、运输振动荷载、挖掘及回采振动荷载等动荷载作用。动荷载会对已有的锚杆支护结构产生损伤,减少锚杆的使用寿命,因此需要针对锚杆研究其在动荷载作用下的受力特性。李强和宿钟鸣等[1]通过现场实测拉拔受力特性分析边坡锚杆支护体系作用机理,探讨了不同土体性质下砂浆锚杆剪应力及轴力的分布形式。姚显春等[2]基于隧道承载岩体变形作为研究基准量,得到因承载岩体发生变形而致使杆体表面存在剪切应力的分布。贾金青等[3]针对预应力锚杆处于分散的压应力作用条件下内部作用机理进行分析,获得该型杆体的微观剪应力和轴力分布的表达式。Farmer[4]对在拉拔荷载作用下锚杆的黏结力做了基础性工作,为后来锚杆体沿锚杆轴向方向的受力特性研究奠定了基础。A.Kilic[5-6]基于锚杆长度、锚杆规格、灌浆材料的水灰比和强度等敏感性因素对全长黏结式锚杆体的锚固力学状态进行了试验研究。尤春安等[7]基于试验得到在拉拔荷载作用下全长黏结式锚杆的受力特性。
然而对锚杆受到横向振动荷载作用下力学特性研究未见报道,而实际工程中锚杆要承受前方掘进工作面爆破传来的横向振动荷载作用。目前,大部分学者针对锚杆横向荷载的研究主要应用于锚杆的无损检测。曾鼎华在2005年为了探索新的锚杆无损检测方法研究了横向冲击荷载作用下锚杆锚固系统的动力响应[8]。薛道成、张凯[9]在2013年对锚杆受横向振动荷载作用下的固有频率进行了研究。不可否认锚杆在爆破振动的过程中轴向受到的作用力较为明显,但在实际测量中发现横向振动同样作用于锚杆并具有与轴向加速度相差无几的加速度。就横向荷载对锚杆的影响问题,目前缺乏理论依据与试验数据等信息。因此,本文通过现场实测数据与室内试验相结合的方式探讨锚杆在受到横向简谐荷载作用后,锚杆黏结受力特性的变化规律。
1 工程实测数据
1.1锚杆监测数据
锚杆实际受力监测是掌握锚杆的受力状态、承载效果的主要手段,在锚杆托盘与围岩之间安装MCS-400型无损锚杆(索)测力计,实测锚杆实际受力及随时间变化规律。在鄂尔多斯市红庆梁煤矿主斜井1 140 m和反掘上山20 m断面处设置观测断面,在顶板中心线靠右一侧和左帮安装2台锚杆测力计。锚杆测力计监测结果如图1所示。
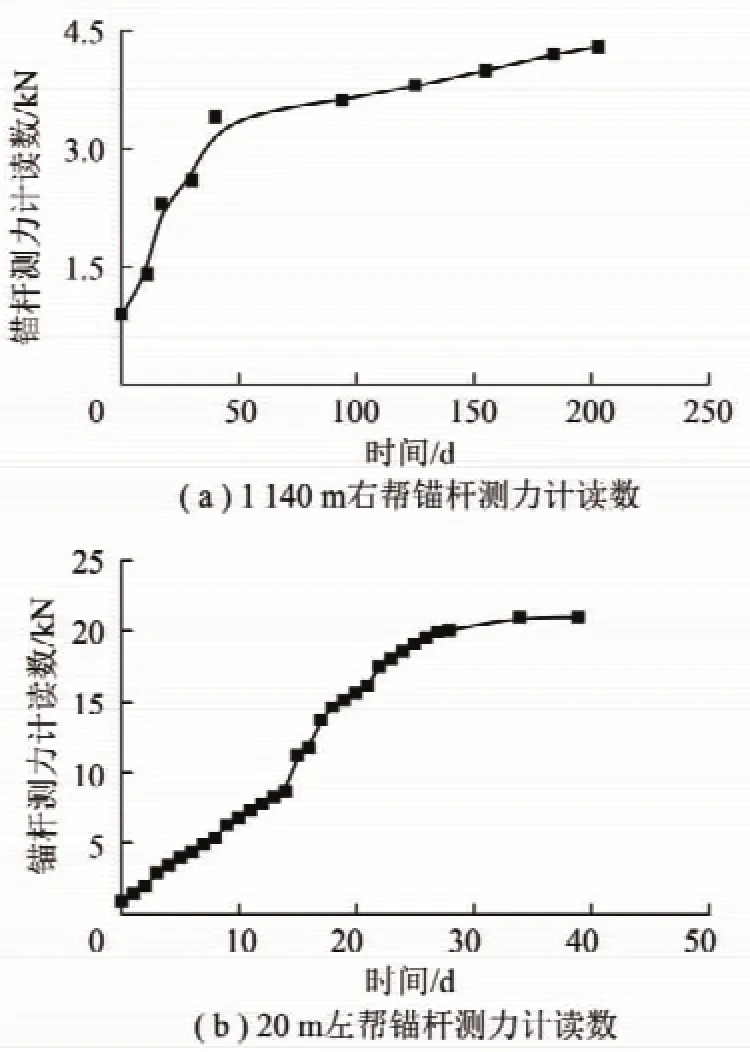
图1 锚杆受力变化情况Fig.1 Stress variation of bolts
由图1可知,锚杆在安装完成后由于继续开挖断面导致支护结构应力发生改变,随着时间的增加,锚杆的受力逐渐增加,28 d后趋于稳定。对于一个设计要求为70 kN的锚杆,从最初的1 kN增加到后来的20 kN,在工作过程中受力也只达到其设计值的1/3。
1.2煤矿爆破荷载作用下围岩振动数据监测
在鄂尔多斯高家梁煤矿矿井中,将振动测试仪[10]放置在巷道底端紧贴巷道侧壁的位置,用耦合剂使其与围岩表面良好接触,并将测量结果运用爆破振动分析软件进行分析。安装仪器与数据测试结果分析如图2,3所示。

图2 放置振动测试仪器Fig.2 Vibration testing instrument position
从图2中仪器的摆放角度可知,通道y即图3中的红色数据曲线表示的是锚杆轴向方向,而x(黑色数据曲线)、z(蓝色数据曲线)则为横向与竖向两个方向。从图3实测数据中可看出在爆破振动的过程中x,y,z三个方向均有振动迹象,且3向加速度出现衰减现象,其加速度最大值可以达到35g,最大振幅为1.5 mm,持续时间1.4 s。经过FFT分析振动主频在11 Hz。
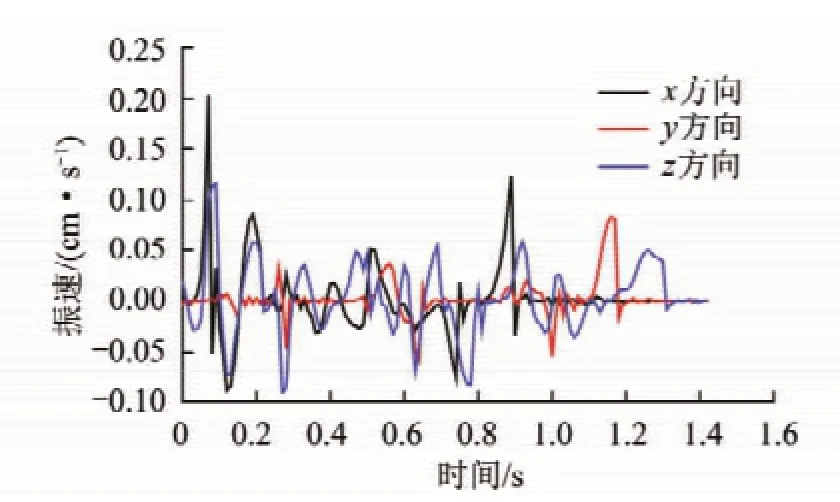
图3 振速时程曲线Fig.3 Curves of vibration velocity
2 工作状态下锚杆横向振动固有频率试验
2.1试验模型设计
2.1.1试验目的
锚杆支护体系在施工过程中和工作状态下会受到动荷载作用,比如爆破荷载、开采掘进的扰动、井下汽车列车行驶过程中的振动等。锚杆支护结构也从原有的单一完成支护围岩控制变形而受到轴向拉力作用发展到静载与动载共同作用,甚至有时动荷载的作用更为突出。巷道掘进的过程中经常采用综掘机挖掘或爆破掘进的方法,掘进与支护穿插进行,刚刚锚固住的锚杆支护体系正在提高强度的过程中会受到掘进工作面爆破动荷载的影响。在振动过程中将出现不同频率的振动荷载,为了避免共振现象的发生,研究锚杆受到横向简谐荷载与轴向拉拔荷载共同作用下锚杆的固有频率有着十分重要的意义。
2.1.2试验材料
(1)光圆钢筋。
本次不同频率横向简谐荷载作用下端锚黏结式锚杆拉拔试验采用Φ18 mm的光圆钢筋,并根据《金属材料室温拉伸试验方法》[11-12]对光圆钢筋的性质进行分析,经过实测得到钢筋实测规格为18.3 mm,抗拉强度为329.3 MPa,伸长率为24.4%。
(2)CS砂浆。
为了缩短试验时间,加快试验进程,需改变砂浆的某些性能,尤其是在减少砂浆的凝固时间和提高强度方面,因此本次试验采用水泥水玻璃砂浆作为黏结锚固体。采用标号为425的普通硅酸盐水泥和浓度为45°Be的水玻璃按照1∶1的比例进行调和,其强度等同于M20[13-14]。
2.1.3试件设计
为研究横向简谐荷载对新装锚杆水泥砂浆的黏结锚固力产生的影响,制作中心黏结试件。基本试件为200 mm×200 mm×510 mm的水泥砂浆试块在其中心位置放置Φ18 mm的光圆钢筋。在制作的过程中先将光圆钢筋放到中心位置并与底部留有10 mm距离,然后灌注水泥砂浆。试验过程参照《JGJ-T70-2009建筑砂浆基本性能试验方法》。
2.2试验过程
本次试验试件采用相同的光圆钢筋与同比例的水泥砂浆,相同的振动加速度取0.5 g,针对不同的振动频率进行试验。首先将3个不受振动荷载的试件直接拉拔后取平均值得到28 d静载极限拉拔力。根据上述现场实测资料显示,锚杆受力大小约为锚杆锚固力设计值的1/3,因此振动的过程中轴向拉拔力为实测静载拉拔力的1/3,并持续加载。将这些处在正常工作状态的锚杆按照不同频率振动20 s后进行拉拔试验,动载试验分10组,每组3个试件,试验后取平均值作为该组试验结果。最终得到不同频率的横向简谐荷载作用下锚杆的黏结力。试验过程如图4~6所示。

图4 未受振动的锚杆拉拔试验Fig.4 Pulling out test without vibration

图5 振动后的锚杆拉拔试验Fig.5 Pulling out test with vibration
2.3试验结果分析
将试验数据进行整理得到表1,在表中可以看到不同振动频率作用下锚杆的实测拉拔力。根据公式(1),通过计算整理可得到锚杆的平均剪应力。

式中,Pu为锚杆体的极限抗拔承载力,kN;d为锚杆体直径,m;Lb为端锚杆体内锚段长度,m;τ为灌浆体与锚杆体交界面位置处的平均剪应力,kPa。

图6 拉拔后的锚杆Fig.6 Bolts after pulling-out
根据表1,得到不同振动频率的横向简谐荷载作用后的极限拉拔力和相应的锚杆黏结应力,将上述数据进行整理并绘制成抗剪强度变化率—振动频率变化曲线,如图7所示。由图7可知,锚杆与水泥砂浆在横向简谐荷载的作用下,随着频率增高其抗剪强度变化率先升高后下降。其中,频率值在40 Hz时抗剪强度变化率最大,可以反映出锚杆水泥砂浆锚固体出现共振现象,锚杆受到横向振动的过程中其固有频率略小于40 Hz。因此在其他试验过程中为了使振动效果更加明显,采用40 Hz作为振动频率。

表1 锚杆极限拉拔荷载Table 1 Load of bolt with ultimate limit pulling-out
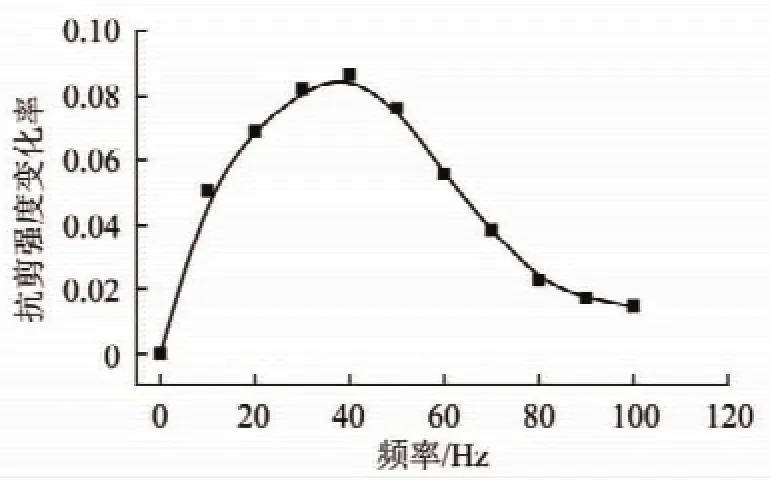
图7 抗剪强度变化率-时间变化曲线Fig.7 Shear stress rate-time curve
3 横向简谐荷载对新装锚杆黏结力影响的模型试验
3.1试验过程
水泥砂浆与锚杆间的黏结力与水泥砂浆龄期、受到振动强度等因素有关。为了研究锚杆与水泥砂浆初凝后受扰动对其黏结性的影响,本次试验试件采用相同的光圆钢筋与同比例的水泥砂浆,针对不同的振动强度和不同的养护龄期进行试验。
试件制作方法同上一组试验。采用添加早强剂水玻璃的水泥砂浆作为灌浆体,经过浇筑凝结硬化等阶段后进行试验。本次试验选取5个龄期分别为6,9,15,24和48 h。每个龄期选取4个试件。分别对应振幅为0.1,0.5和1 mm,振动频率选取40 Hz,振动时间20 s后进行拉拔试验和一个不受振动荷载的试件直接拉拔。通过工程实际测量中第1天锚杆轴力监测数据确定动载锚杆在振动过程中轴向拉力值为1 kN。因此在施加横向简谐荷载的过程中同时施加1 kN轴向荷载。横向振动20 s后直接拉拔至破坏,计算求得不同龄期不同振动强度条件下各锚杆的剪应力。
3.2试验结果分析
将试验数据进行整理并绘制成剪应力变化率-养护龄期变化曲线图和剪应力变化率-振幅变化曲线,得到不同变量作用下对锚杆剪应力产生的影响,并可清楚地展现其变化趋势,如图8,9所示。
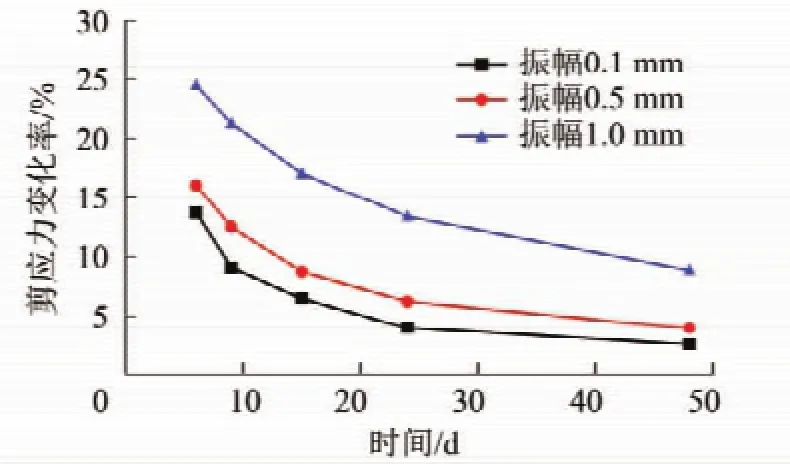
图8 剪应力变化率-养护龄期变化曲线Fig.8 Shear stress rate-time curves
本次试验过程中,水泥砂浆作为黏结锚固剂添加了水玻璃,增加其早强性能,并缩短成型龄期。通过图8和9可以观测到不同龄期的锚杆受到不同强度横向简谐振动荷载作用后的剪应力变化值与变化趋势,并得到以下结论:
(1)不同龄期的锚杆在受到横向简谐荷载作用后其抗剪强度均减小。经过48 h,锚杆受横向简谐振动荷载作用后黏结应力变化率在9%以内,当振动强度较低时,锚杆受振后黏结应力的变化率只有2%。
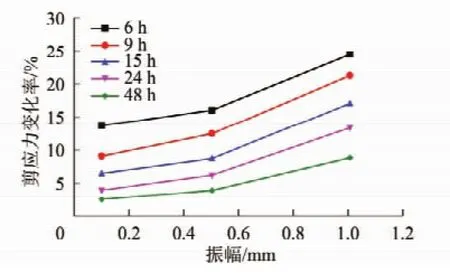
图9 剪应力变化率-振幅变化曲线Fig.9 Shear stress rate-amplitude curves
(2)随着养护龄期的增加,在受到固定强度横向简谐荷载的作用后其剪应力变化率呈下降趋势,其变化率的变化趋势从早期的剧烈变化趋于平缓。24 h内锚杆黏结应力变化率较高,经过24 h后黏结应力变化率趋于平缓。
(3)随着振动强度的增加,锚杆的黏结应力变化率有所提高,剪应力变化率随横向简谐振动的振幅增加(加速度增加)呈非线性增加。
3.3新装锚杆锚固体受振黏结力衰减计算模型
由图8和9可知,随着养护龄期的增加锚杆黏结力变化率在下降,而随着振幅的增加其黏结力变化率在增高。因而可以简单的认为黏结力变化率y正比于振幅X,且反比于养护龄期t,因而定义振幅龄期比为X/t。经过多种方式拟合后发现拟合效果最好,拟合结果如图10所示。
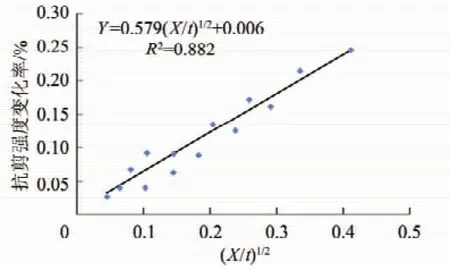
图10 抗剪强度变化率-振幅龄期比拟合曲线Fig.10 Shear strength change rate-amplitude time fitting curve
因此,得到40 Hz,20 s横向振动荷载黏结力变化率与振幅龄期比相应关系式为
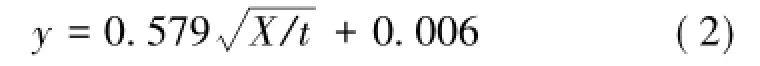
式中,X为振动荷载振幅,mm;t为浇筑完成后养护龄期,s;y为灌浆体与锚杆体交界面位置处的横向振动荷载黏结力变化率。
根据式(2)可对不同龄期不同振幅横向振动荷载作用后锚杆水泥砂浆黏结性进行预测。应用EXCEL软件进行数据处理[14-20],回归分析功能进行分析。确定为2个自变量,分别是养护龄期倒数为X1,振动中振幅为X2,一个因变量剪切强度为y。
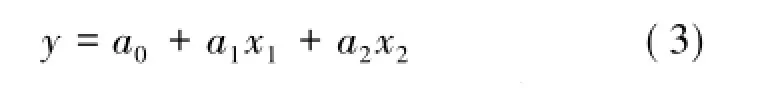
通过Excel软件进行数据处理,复相关系数R2= 0.948 793,拟合较为准确。
y=-0.018 7+0.870 44(1/t)+0.110 92X(4)
由式(4)可得出,养护龄期变量前的系数是振幅前系数的8倍。也就是说,横向简谐荷载与养护龄期耦合作用于新装锚杆的过程中,养护龄期对其黏结力衰减影响起到主导作用。
4 横向简谐荷载作用下端锚黏结式锚杆模型试验
4.1利用均匀设计方法安排试验方案
为了全面研究端锚黏结式锚杆在横向简谐荷载作用下锚固段的力学特性与振动作用对锚杆黏结性的影响,采用均匀设计方法安排试验方案。采用s= 2,D=0.310 0,列号为第1列和第2列,各个因素水平相同,具体试验安排见表2。
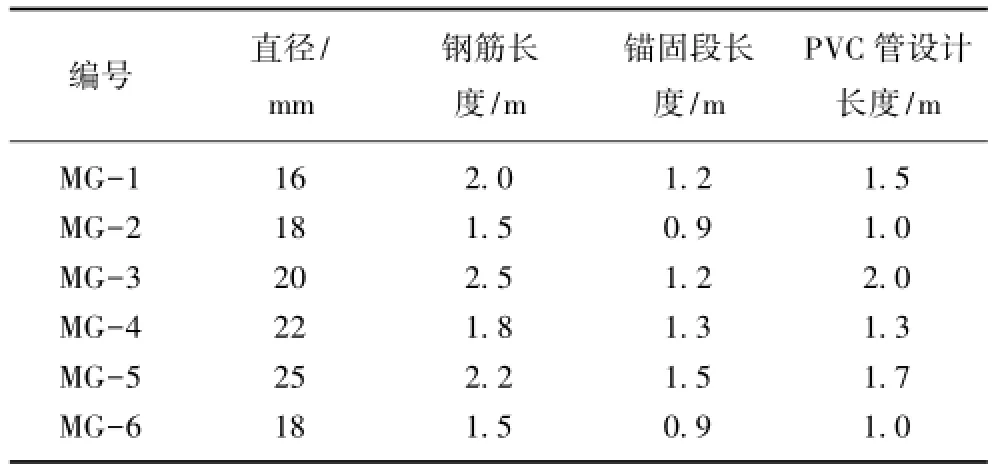
表2 试验安排方案Table 2 Test arrangement plan
4.2锚杆受力特性试验方案
试验分为2部分:其1是根据均匀设计方法设计的5根端锚黏结式锚杆横向简谐振动荷载下的拉拔试验;其2是对1根端锚黏结式锚杆直接进行轴力加载试验。试验加载模型如图11所示。其中MG-1-5试件进行横向简谐荷载试验,加载过程为横向持续施加频率40 Hz振幅0.5 mm的简谐动荷载,轴向用千斤顶进行拉拔试验直至拉断,拉拔过程中每增加10 kN用时20 s,加载方案见表3。
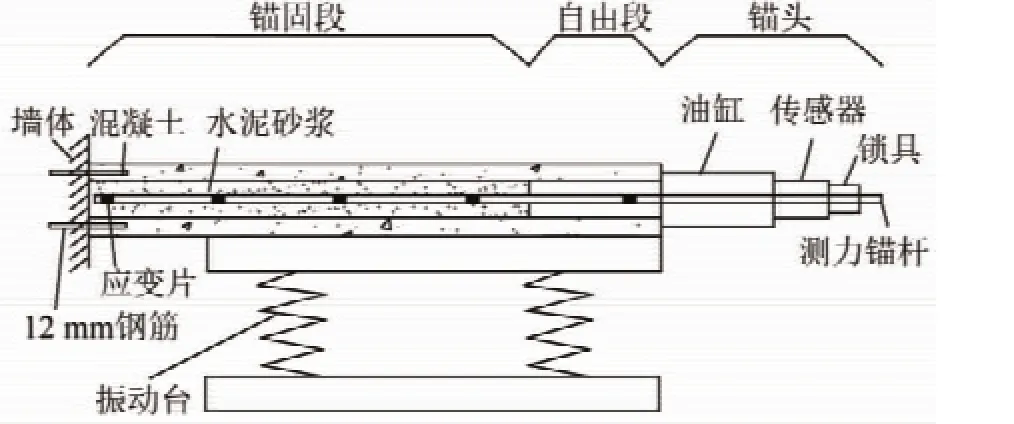
图11 锚杆横向振动试验设计Fig.11 Bolt transverse vibration test design

表3 MG-1-5锚杆横向简谐荷载试验的加载方案Table 3 Loading scheme bolt transverse harmonic load test
4.3试验结果与分析
通过对受到40 Hz,0.5 mm振幅的横向简谐荷载(y=0.5sin 251.2t)作用的锚杆施加不同的拉拔力,测得锚杆沿轴线方向的应力大小。外荷载作用下试件锚杆应力沿轴向的分布情况如图12所示。
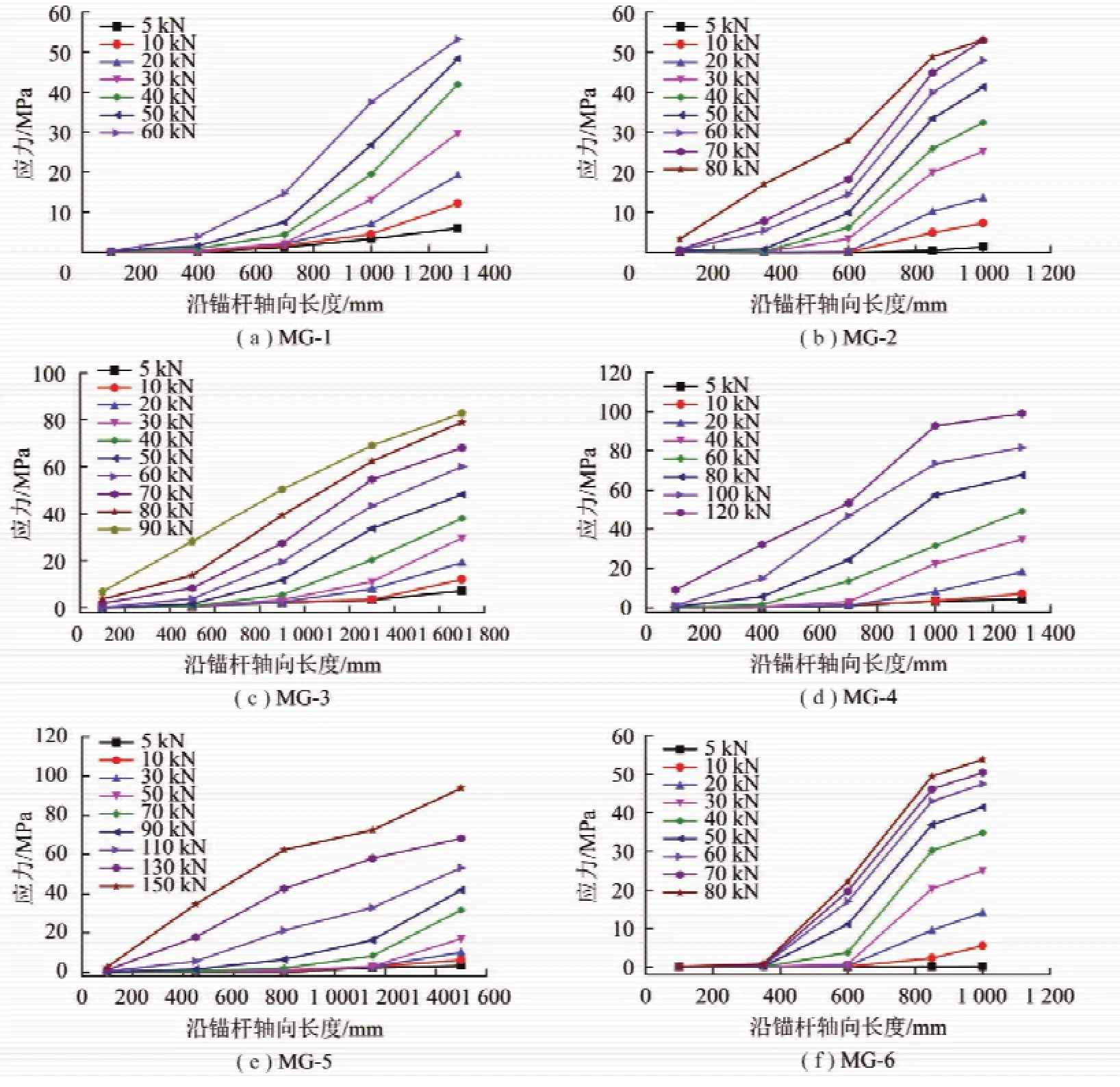
图12 试件沿轴向应力分布Fig.12 Axial stress distribution
从上述的试验数据可得出以下结论:
(1)在端锚黏结式锚杆受到横向简谐荷载作用下,轴向拉拔力一定时,自由段的应力(或应变)数值要大于锚固段的应力应变数值,越靠近锚固段底端应力(或应变)数值越小。锚杆轴向应力曲线类似于1/ 4正弦曲线,随着锚杆拉拔力的增加,锚杆的轴向应力逐渐从自由段向锚杆锚固底端扩散,锚杆锚固最底端数值近似为零。
(2)在静载拉拔试验过程中,锚杆随着拉拔力的增加最初只有1 000 mm处(自由段)和850 mm 处(锚固段接近自由面,900 mm为锚固长度)产生变化。当锚杆拉拔力达到40 kN时,600 mm处才发生变化并且其应力随拉拔力增加的斜率与上述两个测点大致相同,直至拔出100,350 mm处仍无明显变化。
(3)将同样尺寸的MG-2与MG-6锚杆数据进行对比分析,可知在受到横向简谐载荷作用下的锚杆,其应力应变向锚固段底部传递的更快。20 kN时600 mm处发生变化,50 kN时应力应变传递到350 mm处,70 kN时100 mm处开始变化。
根据规范[11],试验测得每个试件的破坏荷载值见表4。

表4 锚杆极限抗破坏荷载Table 4 Ultimate tensile failure load of anchor
从以上试验数据中得到了各点的黏结应变值,将其进行数据处理便可得到每一段上的平均剪切应力值,其计算公式为
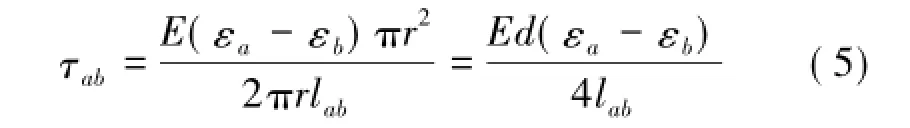
式中,εa为测点 a应变值,%;εb为测点 b应变值,%;r为锚杆体半径,mm;d为锚杆体直径,mm;lab为相邻2个测点之间的相对距离,mm。
从而计算出端锚锚杆体在横向简谐荷载作用下的平均剪应力分布情况,如图13所示。主要选取具有代表性的MG-2试件进行分析,之后的计算部分都取MG-2的测量数值进行计算。根据式(6)可以推导出端锚锚杆体轴向各点的宏观位移分布情况,如图14所示。
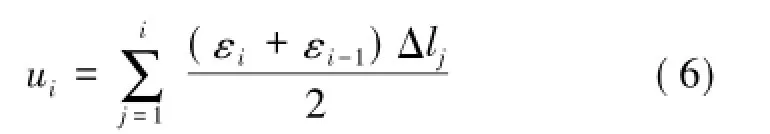
式中,ui为锚杆体两相邻测点间中点位移,mm;εi为锚杆体在i点位置处的微观轴向应变,%;Δlj为相邻两个测点之间的相对长度,mm。
由图13和14可得出以下结论:
(1)起初拉拔力较小时锚固区接近自由面的位置将产生剪应力,依靠黏结力进行工作,并且当拉拔力较小时,随着拉拔力的增加,该位置处的剪应力呈线性增加。
(2)随着拉拔力的增加,剪应力峰值向锚杆底端移动,自由面附近的剪应力开始下降,靠近锚固底端175 mm位置的剪应力增加,且峰值增大。剪应力在向后传递的过程中,锚固段中点位置处的剪应力先增大随后趋于平稳,而其最大值不超过相邻两测点峰值的一半。
(3)靠近锚杆锚固最底端测点的剪应力刚出现,锚杆就被拉拔出来,失去了锚固能力。当荷载继续增大时,锚杆体出现整体滑移现象,滑动摩擦力抵抗外荷载,锚杆失效。试验过程中,将锚杆匀速拉出10 mm的过程中观察拉拔力数值平均为75 kN,与锚杆破坏荷载80.6 kN相差不多。
(4)随着拉拔力的增加,锚杆自由段先产生位移而后逐渐向锚杆底端扩散。从图中可以看出,自由段中锚杆位移-拉拔力斜率要大于锚固段中各点的斜率,只有在接近破坏时锚杆锚固段底部才会出现位移突然增加的现象。
为分析和研究端锚锚杆沿轴线方向剪切应力与滑移产生的位移之间的力学关系,绘制出在不同外载荷作用下各点剪应力-位移曲线,即τ-u曲线,如图15所示。
由图14可知,在锚杆轴向各点位移较小(小于0.1 mm)时,剪应力也较小且呈线性增长趋势。位移继续增加后,剪应力也随之增加但相比前一段斜率变小,图像趋于平缓,到达峰值后随着位移的增加剪应力下降。锚杆自由段到锚杆锚固底端,其剪应力峰值逐渐增加。
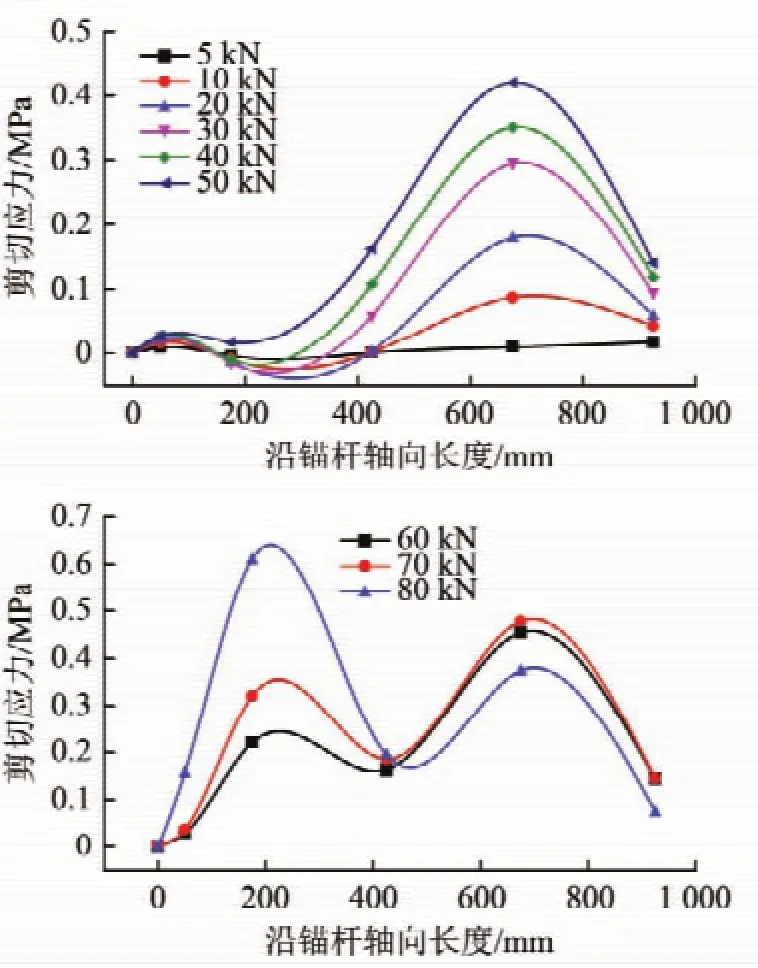
图13 不同载荷作用下沿杆体剪应力分布Fig.13 Shear stress distribution along anchor
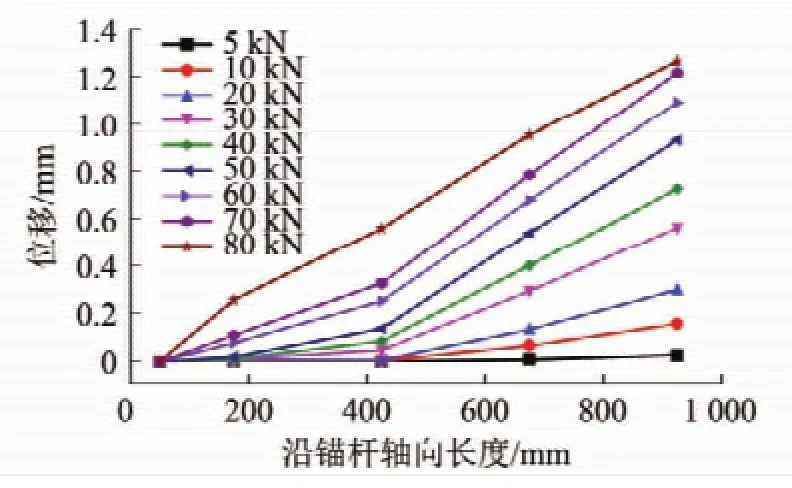
图14 不同载荷作用下杆体位移分布Fig.14 Displacement distribution along anchor
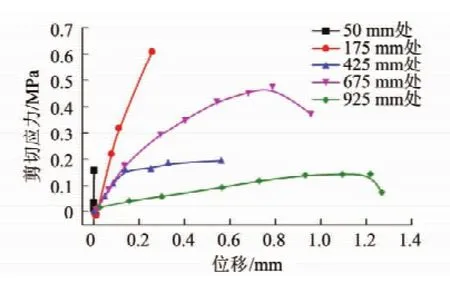
图15 沿锚杆不同位置的曲线Fig.15 Curves along anchor under different measured position
4.4剪切强度分析
通过表3和4中的数据,并利用式(5)计算求解出沿杆体的平均剪切强度值,见表5。

表5 锚杆剪切强度Table 5 Interfacial shearing strength of anchor
按照表5中数据,确定两个自变量,分别是钢筋长度x1和钢筋直径x2,一个因变量剪切强度y,其回归方程为
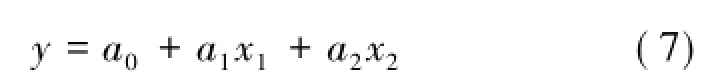
利用Excel软件进行线性回归分析,确定回归方程为y=1.411 022-0.610 75x1+0.057 648x2。其长度的权重是直径权重的10倍,因此锚杆长度因素对锚杆抗剪强度影响的敏感性要强于锚杆直径因素。
5 结 论
(1)通过采集爆破荷载作用过程中锚杆周边围岩的振动信息,发现空间正交的3个方向均有振动迹象,最大加速度为35 g,持续时间1.4 s,振动主频在11 Hz,横向振动荷载对锚杆的影响不可忽视。
(2)通过室内模型试验,将不同振动频率的横向简谐荷载作用于工作状态下的锚杆,得到振动频率与锚杆黏结性衰减的关系。横向振动频率为40 Hz时锚杆黏结力衰减效果最为明显。
(3)获得了新装锚杆锚固体受振黏结力衰减计算模型,横向振动荷载黏结力变化率与振幅龄期比相应关系式为 y=-0.018 7+0.870 44(1/t)+ 0.110 92X,横向简谐荷载与养护龄期耦合作用于新装锚杆的过程中,养护龄期对其黏结力衰减影响起到主导作用。
(4)通过横向简谐荷载作用下端锚黏结式锚杆模型试验,得出了随拉拔力增加锚杆自由段先产生位移而后逐渐向锚杆底端扩散,自由段中锚杆位移-拉拔力斜率要大于锚固段中各点的斜率,只有在接近破坏时锚杆锚固段底部才会出现位移突然增加的现象。
参考文献:
[1]李强,宿钟鸣.拉拔荷载下黄土隧道系统锚杆力学特性分析[J].重庆交通大学学报(自然科学版),2013,32(4):63-68.Li Qiang,Su Zhongming.Drawing load under bolt mechanical characteristics analysis of loess tunnel system[J].Journal of Chongqing Jiaotong University(Natural Science Edition),2013,32(4):63-68.
[2]姚显春,李宁,陈蕴生,等.隧洞中全长黏结式锚杆的受力分析[J].岩石力学与工程学报,2005,24(13):2272-2276.Yao Xianchun,Li Ning,Chen Yunsheng,et al.In the tunnel span of binding bolt stress analysis[J].Journal of Rock Mechanics and Engineering,2005,24(13):2272-2276.
[3]贾金青,涂兵雄,王海涛,等.压力分散型预应力锚杆的力学机理研究[J].岩土工程学报,2011,33(9):1320-1325.Jia Jinqing,Tu Bingxiong,Wang Haitao,et al.Dispersed pressure mechanics mechanism of prestressed anchor study[J].Journal of Geotechnical Engineering,2011,33(9):1320-1325.
[4]Farmer I W.Stress distribution along a resin grouted rock anchor [J].Int.J.Rock.Meeh.Min.Sci.and Geomech.Abstr.,2014,12: 347-351.
[5]Kilic A,Yasar E,Celik A G.Efect of grout properties on the pull-out load capacity of fully grouted rock bolt[J].Tunnelling Underground Space Technology,2012,10:355-362.
[6]Kilic A,Yasar E,Atis C D.Effect of bar shape on the pull-out load capacity of fully grouted rock bolt[J].Tunnelling Underground Space Technology,2012,8:1-6.
[7]尤春安,高明,张利民,等.锚固体应力分布的试验研究[J].岩土力学,2004,25(S):63-66.You Chun’an,Gao Ming,Zhang Limi,et al.Stress distribution of anchor solid experimental study[J].Rock and Soil Mechanics,2004,25(S):63-66.
[8]曾鼎华.横向冲击荷载作用下锚杆锚固系统的动力响应研究[D].重庆:重庆大学,2013.Zeng Dinghua.Transverse dynamic response of bolt anchorage system under the shock load research[D].Chongqing:Chongqing University,2013.
[9]薛道成,张凯.煤矿锚杆锚固系统横向振动特性研究[J].中国矿业大学学报,2013,8(7):695-700.Xue Daocheng,Zhang Kai.Coal mine bolt anchorage system characteristics of transverse vibration study[J].Journal of China University of Mining,2013,8(7):695-700.
[10]李夕兵,凌同华,张义平,等.爆破震动信号分析理论与技术[M].北京:科学出版社,2009.
[11]GB/2282002.金属材料室温拉伸试验方法[S].
[12]庞宗霞,田利民.水泥-水玻璃浆液的室内试验与研究[J].山西交通科技,2010(5):15-16.Pang Zongxia,Tian Limin.Silicate cement grout indoor test and re-search[J].Journal of Shanxi Traffic Science and Technology,2010(5):15-16.
[13]JGJ-T70-2009.建筑砂浆基本性能试验方法[S].
[14]关成立.基于敏感性及可靠性的边坡稳定性研究[D].昆明:昆明理工大学,2006.Guan Chengli.Based on the sensitivity and reliability of slopestabilitystudy[D].Kunming:Kunming University of Scienceand Technology,2006.
[15]孟超,李学华.沿空掘巷锚杆支护参数敏感性分析与应用[J].中国煤炭,2013,39(3):45-49.Meng Chao,Li Xuehua.Roadway driving along goaf bolt support parameters sensitivity analysis and application[J].Journal of China Coal,2013,39(3):45-49.
[16]贾宝新.锰铁废渣作为路面基层稳定土的试验研究[J].辽宁工程技术大学学报,2003,26(2):97-101.Jia Baoxin.Ferromanganese slag as pavement base stabilized soil experimental research[J].Liaoning University of Engineering Science,2003,26(2):97-101.
[17]刘文卿.实验设计[M].北京:清华大学出版社,2005,33(11): 188-193.
[18]刘华,万建平.均匀试验设计的方法与应用[J].阜阳师范学院学报(自然科学版),2013,20(1):12-16.Liu Hua,Wan Jianping.Methods and application of uniform experimental design[J].Journal of Fuyang Normal College(Natural Science Edition),2013,20(1):12-16.
[19]邵丹,周业明.回归常数的显著性检验[J].科学技术与工程,2014,7(8):1715-1716.Shao Dan,Zhou Yeming.Significance test of regression constant [J].Science,Technology and Engineering,2014,7(8):1715-1716.
[20]CECS22.2005岩土锚杆(索)技术规程[S].
[21]梁广昌.简谐波作用下锚杆数值模拟分析[J].广东工业大学学报,2013,8(12):266-271.Liang Guangchang.Bolt under simple harmonic function numerical simulation analysis[J].Journal of Guangdong University of Technology,2013,8(12):266-271.
[22]崔千里,林健.树脂锚杆锚固特性数值模拟研究[J].煤炭工程,2013(S1):100-103.Cui Qianli,Lin Jian.Resin anchor rod anchor features numerical simulation study[J].Journal of Coal Engineering,2013(S1):100-103.
[23]康红普,崔千里,胡滨,等.树脂锚杆锚固性能及影响因素分析[J].煤炭学报,2014,39(1):110-116.Kang Hongpu,Cui Qianli,Hu Bin,et al.Resin anchoring bolt anchorage performance and influence factors analysis[J].Journal of China Coal Society,2014,39(1):110-116.
中图分类号:TD353
文献标志码:A
文章编号:0253-9993(2016)06-1407-09
收稿日期:2015-09-14修回日期:2015-12-26责任编辑:常琛
基金项目:国家自然科学基金煤炭联合基金资助项目(51174268)
作者简介:张哲诚(1990—),男,吉林长春人,博士。E-mail:610360001@qq.com。通讯作者:张向东(1962—),男,教授,博士生导师,博士。E-mail:jwd101@126.com
Experimental research of anchors bonding mechanical properties under transverse harmonic loads
ZHANG Zhe-cheng,ZHANG Xiang-dong,LIU Yuan-hao,LI Qing-wen
(College of Civil Engineering and Transportation,Liaoning Technical University,Fuxin123000,China)
Abstract:There is an urgent need to study the micro mechanical properties and the adhesion variation of bolt under dynamic load as a consequence of the effect of mining load and blasting load on the existing bolt supporting.Based on engineering practice,the axial force variation under working conditions and the vibration information of surrounding rock around anchor bolt under the load of blasting vibration were monitored.Formula was obtained through indoor test for calculating the attenuation law of anchor bond in anchor rod under the coupled action of the working age and the vibration strength with lateral vibration inherent frequency under axial loads.In addition,a device was developed for conducting anchors grouted bolt model experiment under transverse harmonic loads.Using the uniform design method,considering two influencing factors including bolt length and bolt diameter,through dynamic monitoring system,the bolt transverse harmonic load stress distribution along the length of anchor bolt,the relationship between stress distribution and drawing force,and the relationship between shear stress and displacement were obtained.Finally,using software FLAC3D,the mechanical model of bolt and rock interaction was established.
Key words:transverse harmonic load;anchor natural frequency;adhesion decay;maximum bolting force

