动静阻尼影响下锚杆瞬态动力响应的解析解及工作状态预测

孙　冰，梁展平，曾　晟，肖佳辉，付志国，黄振江

(1．南华大学土木工程学院，湖南衡阳　421001;2．南华大学核资源工程学院，湖南衡阳　421001)



动静阻尼影响下锚杆瞬态动力响应的解析解及工作状态预测

孙冰1，梁展平1，曾晟2，肖佳辉1，付志国1，黄振江1

(1．南华大学土木工程学院，湖南衡阳421001;2．南华大学核资源工程学院，湖南衡阳421001)

摘要:为了分析动静阻尼条件下锚杆的瞬态动力响应特征以及荷载与锚杆振动基频之间的相互关系，在考虑锚固介质对锚杆产生的动态与静态阻尼力的影响下，基于波动理论建立了锚杆受瞬态激振时引起弹性振动的波动方程。在一端固定一端自由的边界条件下，求解锚杆位移场的解析解，得到基频与荷载之间呈二次幂函数关系。为了验证理论分析的结果，采用室内模型锚杆的拉拔试验和无损检测试验，对不同加载等级下的动测信号进行频谱分析得出对应的基频，采用最小二乘法拟合得到荷载与基频之间的函数关系也呈二次幂函数关系，且施加的荷载小于锚杆体与锚固介质间的握固力时，荷载与基频呈正相关关系，荷载大于握固力时，二者呈负相关关系，这与理论分析结果基本吻合。

关键词:锚杆;瞬态动力响应;动静阻尼;工作状态;振动基频

孙冰，梁展平，曾晟，等．动静阻尼影响下锚杆瞬态动力响应的解析解及工作状态预测［J］．煤炭学报，2016，41(6):1400－1406．doi:10．13225/j．cnki．jccs．2015．1310

Sun Bing，Liang Zhanping，Zeng Sheng，et al．Analytical solution of transient dynamic response and working condition prediction of bolt considering dynamic and static damping［J］．Journal of China Coal Society，2016，41(6):1400－1406．doi:10．13225/j．cnki．jccs．2015．1310

锚杆作为一种简单的主动支护结构，能最大限度地保持围岩的完整性和稳定性，控制围岩变形、位移和裂缝的发展。因其具有成本低廉、加工简便、安装方便、施工速度快等优点［1－3］，其在岩土工程领域中得到了广泛的应用，并且取得了丰硕成果及社会经济效益［4－5］。但由于其自身的隐蔽性、工作环境的复杂性、设计、施工与管理的不确定性;在使用过程中，随着环境的作用和变迁，整个系统也在不断地调整变化或者产生病害，严重影响了锚杆的正常工作状态。因此，影响锚杆工作状态的锚固质量和锚杆承载力成为岩土工程界亟待解决的重要问题［6－8］。

在锚杆锚固质量检测研究方面，用拉拔法来检测锚杆质量的方法出现较早，但拉拔不可避免的对锚杆造成影响，甚至失效，所以其在工程应用中存在局限性。无损检测技术日益受到广大工程技术人员和学者的关注［9－11］。为了提高锚杆锚固质量的无损检测精度，国内外许多专家学者进行了研究，并取得了一定成果［12－15］，但大多的研究未考虑荷载的影响。在实际的安装使用过程中，锚杆或多或少都在承受荷载的作用，实际工程检测也是在荷载作用的前提下进行的，若研究忽略了荷载作用，将使所得参数及其变化与实际的情况存在较大差别，更无法精确合理的指导工程实践。锚杆在整个工作过程中，其工作荷载随围岩变形、碎胀和失稳变化而改变，不仅与锚杆自身的结构和材料特性有关，而且与围岩的强度、变形特征及可锚性密切相关，是锚杆和围岩相互作用的本质体现，也是影响锚杆支护结构及围岩稳定性的关键参数。锚杆在纵向振动时，基频与锚杆的锚固状态和锚固长度密切相关，可以通过基频有效地评价锚杆的锚固质量［16－17］。刘海峰等［18］进行了锚杆工作状态的无损检测研究，在荷载较小的条件下得到了基频与工作荷载的关系式，为基于动测法确定锚杆工作载荷的范围提供了依据，但较大等级荷载下的工作状态需要进一步研究。在不考虑阻尼的情况下，对两端自由的锚杆，基频等于各阶振型频率之差;对一端固定一端自由的锚杆，基频等于各阶振型频率之差的2倍［19］。全锚锚杆的振动要比前2种情况复杂很多，端锚锚杆锚固长度短锚固质量较差，故采用锚固长度长锚固力高的加长锚固锚杆。因此，本文针对加长锚固锚杆(下文中简称锚杆)采用一端固定一端自由的锚杆模型，考虑锚固介质对锚杆产生的动态与静态阻尼力的影响，建立锚杆受瞬态激振时引起弹性振动的波动方程，求解位移场的解析解，探求大小等级荷载下锚杆基频与荷载之间的关系，并通过实验研究验证理论分析结果的可靠性。

1　锚杆的瞬态动力响应

1.1低应变条件下锚杆的纵向振动的波动方程

锚杆在低应变纵向振动时，将其简化为一维杆件建立波动方程，在锚杆微元体的分析因素中加入动静阻尼系数，并假定锚杆的受激振动在弹性限度内、锚杆材料均匀或分段均匀且各向同性、锚杆受激振动时其截面保持为平面。如图1所示，用x表示杆中某一横截面的坐标，u(x，t)表示对应横截面的纵向位移。取一微小单元体，单元体承受随时间变化的动应力σ(x，t)。引入达朗贝尔解法［20］中的抗剪刚度k，即锚杆侧单元发生单位位移时，周围介质对锚杆侧反向的静阻力;考虑摩擦阻力，设单元体随速度变化的摩擦阻尼系数为β，即锚杆单元以单位速度运动时，介质对锚杆产生动阻力。对单元体进行受力分析得x方向上的运动平衡方程为

式中，A为杆的横截面面积;ρ为杆的质量密度。

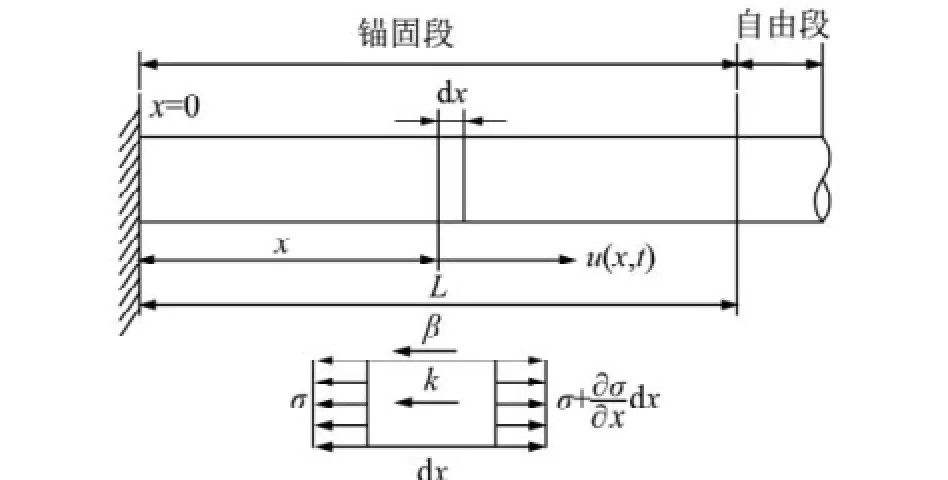
图1　细长杆及作用在微小单元体上的应力Fig.1　Thin rod and the stress of the tiny unit cell stressed by the rod

根据等截面假设，式(1)可以化简为式(2):

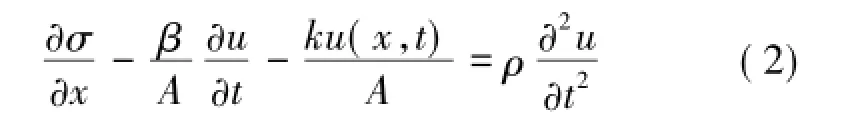
根据胡克定律，有

式中，E为弹性模量;ε为轴向应变，则

根据式(3)和(4)，式(2)化简为

当杆为非均匀杆件时，弹性模量E和密度ρ可不取常数，而可表达为 x的函数，即 E=E(x)和 ρ= ρ(x)。如果杆是均匀的，E和ρ是常数，则式(5)化简为

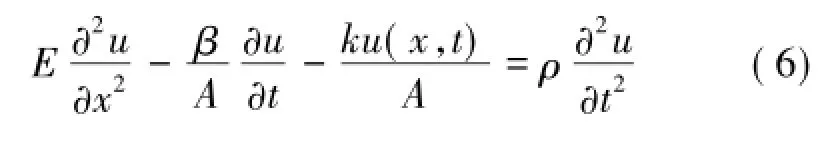
即

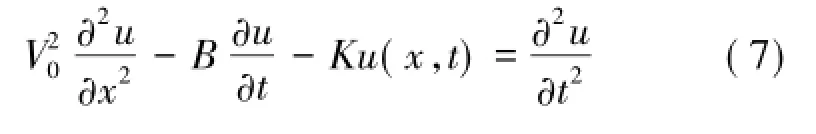
式中，B为等效阻尼系数，B=β/(Aρ);K为等效弹性系数，K=k/(Aρ);V0为应力波沿锚杆纵向传播的速度，。

1.2初始条件及边界条件

(1)初始条件。

在锚杆锚固段的外端面(x=L，即锚固段与自由段交界面处)处受一瞬时冲击力作用，根据动量定理，锚杆顶面将获得一个初速度，如式(9):

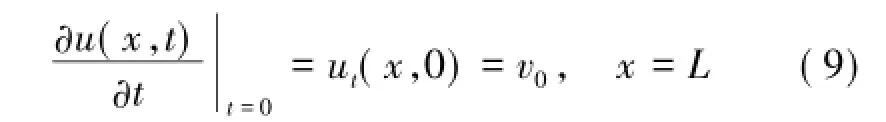
引入Dirac函数δ(x)，有

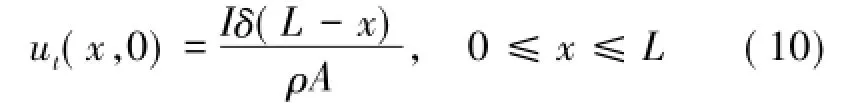
式中，I为瞬时冲击力对锚杆的冲量。

(2)边界条件。

在实际工程中，基岩一般较硬，故可将锚固体末端作为固定端处理，另一端则为自由端，其边界条件为

1.3锚杆瞬态响应的解析解

采用特征值法，式(7)有如下形式的解

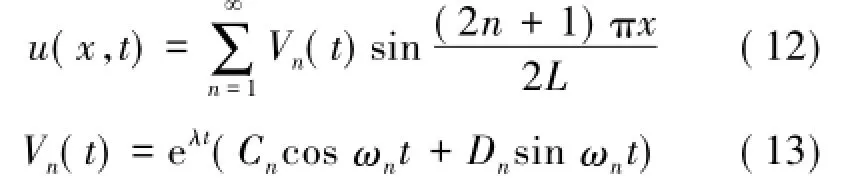
由式(12)和(13)得位移方程，如下:

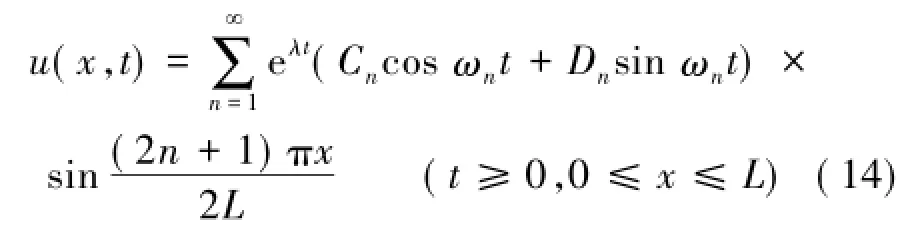
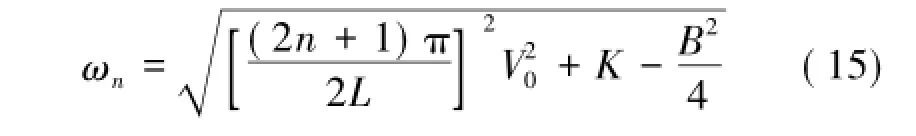
式中，ωn为角频率;λ=－B/2;Cn，Dn为待定系数。

由初始条件方程式(8)可得Cn=0，于是式(14)化简为

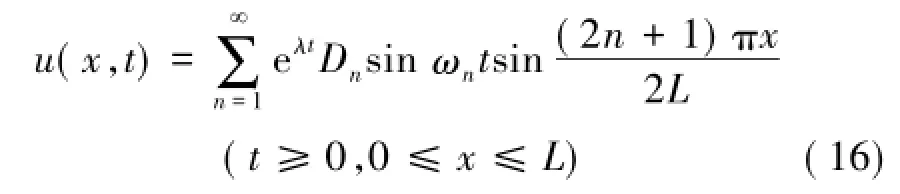
由速度初始条件有:

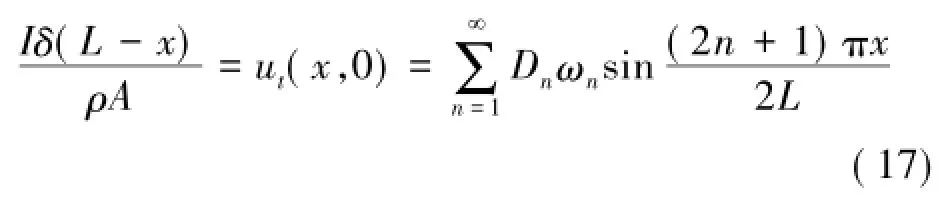
由广义傅里叶级数展开，可得:

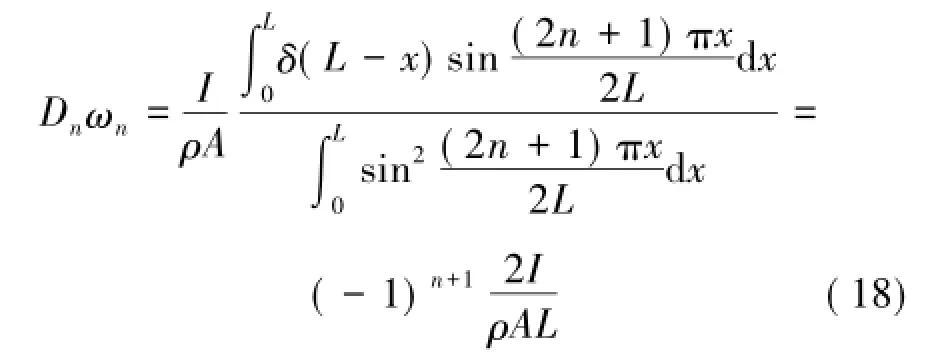
将式(18)代入式(16)可得锚杆位移响应方程如下:

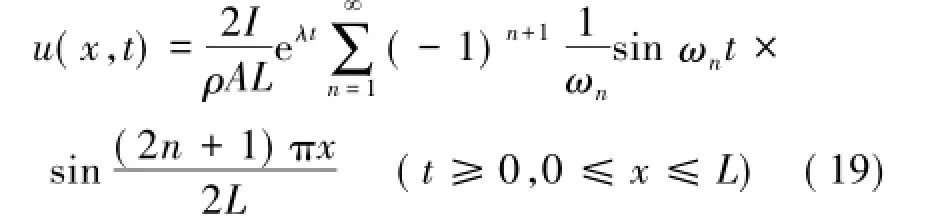
1.4算例分析

笔者在Matlab环境下，依据本文所得解析解及必要参数，编制了锚杆瞬态激振下位移响应的计算程序。具体参数为:锚固长度1 900 mm，锚杆直径25 mm，抗剪刚度 3.6×106N/m，瞬时冲量为0.025 N/s。所得模拟锚杆受激振时的位移响应曲线如图2所示。

图2　锚杆的解析解位移响应曲线Fig.2　Analytical solution displacement response curve of bolt

由图2可知，在5 ms内，锚杆的振动以正弦方式出现多次固端反射和底端反射，且固端反射信号较强而底端反射信号微弱，这与一般的锚杆位移响应特征相似。另外，由于阻尼的影响使应力波发生扩散、散射以及吸收等现象，消耗了应力波的能量，从而使得响应曲线在短时间内衰减非常明显。因此，上述现象验证了解析解的可靠性。

2　锚杆工作荷载与基频的关系

其中，T为作用在锚杆上的荷载。将式(20)代入式(13)得锚杆振动基频与荷载之间的关系为

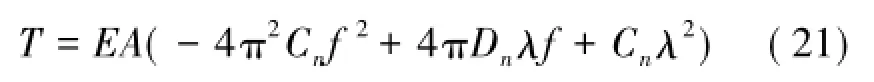
式中，f=ω/(2π)为振动频率，由式(21)可知，作用在锚杆上的荷载与振动频率之间呈幂函数关系。

在采用频域分析的方法进行锚杆锚固质量判断时，基频是非常重要的参数，因为锚杆受激振动时的总能量是按各次谐振频率进行分配的。锚杆各频率成分的能量占总能量的比率为

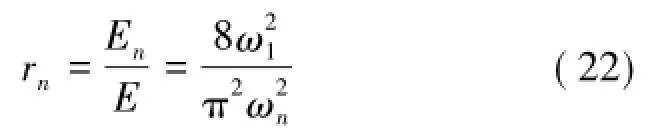
锚杆在瞬态激振下，产生低应变，故式(15)可以近似写为

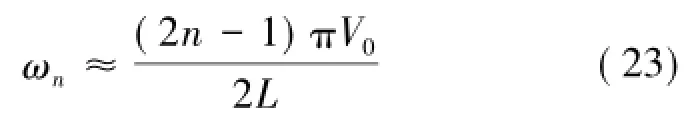
将式(23)代入式(22)得

由式(24)可知，基频能量占总能量的大部分，约80%。锚杆在纵向振动中，其振动的模态对横向模态而言相对单一，基频比较明显，主要可以用基频来衡量瞬态激振下锚杆的振动特性。锚杆锚固长度越长，基频越高，锚固质量越好。

3　试验验证

3.1测试方法与测试系统

基于应力波反射法，采用力锤垂直激振锚杆外端产生冲击荷载。测试系统由动态信号测试分析仪、压电式力锤、压电式加速度传感器、信号放大器、数据采集仪、控制器、微机处理系统等组成。力锤为江苏联能Lc冲击锤，重2.5 g，电荷灵敏度3.57 PC/N。动态信号分析仪为杭州亿恒AVANT－10，为了避免在采样时出现频率折叠现象，采样频率至少取带限信号最高频率的2倍，故采样频率采用100 kHz，采样点数4 096个，分析频宽38.4 kHz。压电式加速度传感器5个，频率范围为0.5～10 kHz，灵敏度为2.47 Pc/ m/s2。对锚杆进行加载，采用50 t穿心千斤顶。

3.2模型试验

室内模型锚杆采用长2.4 m、直径28 mm的III级螺纹钢筋，外露长度为0.5 m，砂浆配合比为1∶2∶4。以直径200 mm的PVC管为模板，采用先插杆后注浆的施工方式，锚杆结构简图如图3所示。加速度传感器布置在锚固段与自由段的交界面处。

图3　锚杆结构简图Fig.3　Structural scheme and arrangement of measuring points

3.3结果分析

基频综合反映锚杆、锚固介质和围岩3者之间的握裹程度、参与振动质量的大小及有效锚固段上界面接近刚性连接的程度，可以通过锚杆动测信号的频谱分析得到。通过计算得出钢筋发生屈服时所对应的轴向拉力设计值即锚杆的极限承载力约为250 kN，此时锚杆将出现明显位移。在实际工程中，锚杆验收试验时的加荷等级常取最大实验荷载的10%;试验中，为了获得更精确的试验结果，取加载步长为10 kN。在对锚杆施加一个稳定的拉拔荷载后，用力锤对锚杆端头垂直施加一个小冲击，测定在该等级荷载下锚杆的变形与加速度响应曲线如图4所示(图中仅列出了部分加载等级下的动测曲线)。通过对加速度时程曲线进行快速傅里叶变化，得出各等级荷载下对应的基频见表1。

在锚杆无损检测信号中，阻尼的存在会使信号强度逐渐衰减，从图4的信号分析可以看出，在初期，加速度的幅值振动较大，但是衰减也较快;在后期，信号衰减变得十分缓慢，且在对单个测点信号进行阻尼分析时，所得到的阻尼变化情况仅为单个点的情况，不能综合反映整个锚杆的阻尼变化情况。因此在讨论荷载对阻尼的影响时不能通过分别计算阻尼值的大小来直接进行讨论，然而从另一个角度出发，阻尼的作用在于对初始能量脉冲的能量消耗，可以通过对两个传感器信号的起跳点的幅值比变化情况进行分析，以判断阻尼的变化情况。从图4可知，锚杆的底端反射与首波的幅值比呈逐渐增加趋势，而固端反射与首波幅值比呈逐渐减少趋势，其原因在于当荷载达到一定值时，锚杆与周围介质的粘结界面受到破坏，界面的握裹作用越小，锚杆底端反透射越强烈。

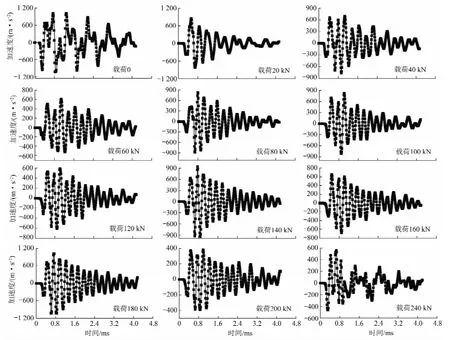
图4　不同荷载下锚杆的动测加速度信号Fig.4　Acceleration response signals of bolt under different load

表1　荷载与基频的实测Table 1　Measured values of different load and frequency

采用最小二乘法对表1中的数据进行分析处理，得基频与荷载间的回归方程(25)和拟合曲线如图5所示。

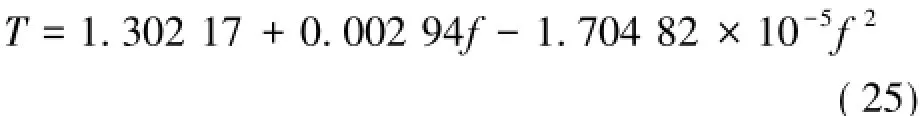
由回归方程(25)和拟合曲线图5可知，在荷载作用下，锚杆的荷载与基频关系曲线的回归方程为2次幂函数，与理论分析吻合，相关系数达0.918以上。

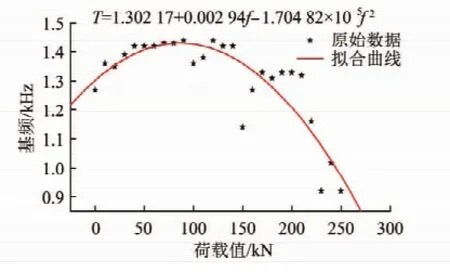
图5　实测基频与荷载关系的拟合曲线Fig.5　Fitting curve of the measured load and frequency

由表1和图4可知，当荷载比较小时，随着荷载的增加，锚杆锚固系统的振动频率逐渐增大。在一定等级范围内，基频的变化比较平缓;当荷载达到一定值时，试验中为120 kN，振动频率达到最大值，经计算该荷载值与锚杆体和锚固介质发生滑移时由于克服黏结面摩擦所需要施加的轴向拉力即握固力接近;随着荷载继续增加甚至达到极限承载力，振动频率反而减小，而且频率的减小随着荷载的增加而加剧。原因在于，随着荷载增加界面的连接受到破坏，锚固介质的抗剪强度减小，参与振动质量的能量减小，从而使得基频减小。整体而言，锚杆的基频较为稳定，但其在不同荷载下，各频带能量分布有明显的差异。

4　结　　论

(1)考虑周围介质对锚杆产生的动静阻尼的影响，建立了锚杆受瞬态激振时的阻尼波动方程，推导了其位移场的解析解。若对位移的时间变量和空间变量求导，可得速度、加速度和应力应变。在实际工程中，可以根据具体需求求解不同的场量并与工程实际对比，指导实际检测问题;同时，并根据工程经验修正该解析解，或者探求更简单的数值解或近似解。

(2)阻尼的存在引起对初始脉冲的能量消耗，表现为信号强度的逐渐衰减，阻尼的变化可以通过幅值比的变化来衡量。

(3)通过理论分析和实验验证得出，无论在大小等级荷载作用下，荷载与振动频率之间均呈二次函数关系，相关系数达0.918以上。当施加的荷载小于锚杆体与锚固介质间的握固力时，荷载与基频呈正相关关系;但当荷载大于握固力时，二者呈负相关关系，直到锚杆达到极限承载力而发生破坏。

(4)在实际工程中可以根据锚杆动测信号的频谱分析，得到对应荷载下的基频，根据拟合函数可以得到对应的工作荷载，还可以预测锚杆的握固力和极限承载力。

参考文献:

［1］康红普，崔千里，胡滨，等．树脂锚杆锚固性能及影响因素分析［J］．煤炭学报，2014，39(1):1－10．Kang Hongpu，Cui Qianli，Hu Bin，et al．Analysis on anchorage performances and affecting factors of resin bolts［J］．Journal of China Coal Society，2014，39(1):1－10．

［2］王刚，刘传正，吴学震．端锚式锚杆－围岩耦合流变模型研究［J］．岩土工程学报，2014，36(2):363－375．Wang Gang，Liu Chuanzheng，Wu Xuezhen．Coupling rheological model for end-anchored bolt and surrounding rock mass［J］．Chinese Journal of Geotechnical Engineering，2014，36(2):363－375．

［3］Wu R，Xu J，Li C，et al．Stress wave propagation in supporting bolts: a test for bolt support quality［J］．International Journal of Mining Science and Technology，2012，22(4):567－571．

［4］刘洪涛，王飞，蒋力帅，等．顶板可接长锚杆耦合支护系统性能研究［J］．采矿与安全工程学报，2014，31(3):366－372．Liu Hongtao，Wang Fei，Jiang Lishuai，et al．On the performance of lengthened bolt coupling support system in roadway roof［J］．Journal of Mining＆Safety Engineering，2014，31(3):366－372．

［5］单仁亮，孔祥松，蔚振廷，等．煤巷强帮支护理论与应用［J］．岩石力学与工程学报，2013，32(7):1304－1314．Shan Renliang，Kong Xiangsong，Wei Zhenting，et al．Theory and application of strong support for coal roadway sidewall［J］．Chinese Journal of Rock Mechanics and Engineering，2013，32(7):1304－1314．

［6］薛道成，吴宇，张凯．煤矿锚杆轴向受力无损检测试验研究与应用［J］．采矿与安全工程学报，2013，30(3):375－379．Xue Daocheng，Wu Yu，Zhang Kai．Experimental study and application on non-destructive testing of bolt axial force in coal mine［J］．Journal of Mining＆Safety Engineering，2013，30(3):375－379．

［7］杨天春，吴燕清，夏代林．基于相位推算法的锚杆施工质量无损检测分析方法［J］．煤炭学报，2009，34(5):629－633．Yang Tianchun，Wu Yanqing，Xia Dailin．An analytic method for rock bolt’s non-destructive testing signals by phase deducted method ［J］．Journal of China Coal Society，2009，34(5):629－633．

［8］Thurner H F．Boltomee-Instrument for nondestructive testing of grouted rock bolts［A］．Proceedings of the 2nd International Symposium on Field Measurements in Geomachanics［C］．Balkema，Rotterdam: A A Balkema，1988:135－143．

［9］汪明武，王鹤龄．锚固质量的无损检测技术［J］．岩石力学与工程学报，2002，21(1):126－129．Wang Mingwu，Wang Heling．Nondestructive testing of anchoring quality［J］．Chinese Journal of Rock Mechanics and Engineering，2002，21(1):126－129．

［10］Zou D H，Cui Y，Madenga V，et al．Effects of frequency and grouted length on the behavior of guided ultrasonic waves in rock bolts［J］．International Journal of Rock Mechanics＆Mining Science，2007，40:813－819．

［11］孙冰，郑绪涛，曾晟，等．多点布测下锚固缺陷诊断的小波多尺度分析［J］．煤炭学报，2013，33(3):305－310．Sun Bing，Zheng Xutao，Zeng Sheng，et al．Multi-scale analysis on anchoring defects diagnosis under multiple measuring points［J］．Journal of China Coal Society，2013，33(3):305－310．

［12］李义，张昌锁，王成．锚杆锚固质量无损检测几个关键问题的研究［J］．岩石力学与工程学报，2008，27(1):108－116．Li Yi，Zhang Changsuo，Wang Cheng．Study on several key issues in nondestructive detection of bolt bonding integrality［J］．Chinese Journal of Rock Mechanics Engineering，2008，27(1):108－116．

［13］Zhang C S，Zou D H，Madenga V．Numerical simulation of wave propagation in grouted rock bolts and the effects of mesh density and wave frequency［J］．International Journal of Rock Mechanics ＆Mining Sciences，2006，43:634－639．

［14］Beard M D，Lowe M J S．Non-destructive testing of using guided ultrasonic waves［J］．International Journal of Rock Mechanics and Mining Sciences，2003，40:527－536．

［15］陈建功，胡俊强，张永兴．基于完整锚杆动测技术的围岩质量识别研究［J］．岩土力学，2009，30(6):1799－1804．Chen Jiangong，Hu Junqiang，Zhang Yongxing．Identification of sur-rounding rock quality based on dynamic testing technology of integrated anchor［J］．Rock and Soil Mechanics，2009，30(6):1799－1804．

［16］Stillborg B．Analytical models for rock bolts［J］．International Journal of Rock Mechanics and Mining Sciences，1999，36(8):1013－1029．

［17］Yasar E，Celik A C．Effect of grout properties on the pull-out load capacity of fully grounted rock bolt［J］．Tunneling and Underground Space Technology，2002，17(4):355－362．

［18］刘海峰，杨维武，李义．锚杆工作荷载实时检测技术研究［J］．矿业研究与开发，2008，28(2):54－57．Liu Haifeng，Yang Weiwu，Li Yi．Research on real time test technique of working load of anchorage bolt［J］．Mining Research and Development，2008，28(2):54－57．

［19］王猛．应力波锚杆锚固质量无损检测技术实验研究［D］．太原:太原理工大学，2012．Wang Meng．Experiment research on stress wave nondestructive testing technology for bolt anchorage quality［D］．Taiyuan:Taiyuan University of Science and Technology，2012．

［20］王奎华．基桩波动方程达朗贝尔解法精度研究［J］．岩石工程学报，1999，21(5):617－620．Wang Kuihua．A study on the accuracy of d’Alembert solution to pile wave equation［J］．Chinese Journal of Geotechnical Engineering，1999，21(5):617－620．

中图分类号:TD353

文献标志码:A

文章编号:0253－9993(2016)06－1400－07

收稿日期:2015－09－10修回日期:2015－12－27责任编辑:常琛

基金项目:国家自然科学基金资助项目(51204098);湖南省科技厅重点研发计划资助项目(2015SK2058－4);湖南省重点学科建设资助项目

作者简介:孙冰(1979—)，女，河南平顶山人，副教授。Tel:0734－8282594，E－mail:sunbingzs@126．com。通讯作者:曾晟(1977—)，男，湖南常德人，副教授。Tel:0734－8282230，E－mail:usczengs@126．com

Analytical solution of transient dynamic response and working condition prediction of bolt considering dynamic and static damping

SUN Bing1，LIANG Zhan-ping1，ZENG Sheng2，XIAO Jia-hui1，FU Zhi-guo1，HUANG Zhen-jiang1
(1．School of Civil Engineering，University of South China，Hengyang421001，China;2．Nuclear Resources Engineering College，University of South China，Hengyang421001，China)

Abstract:In order to analyze the characteristics of transient dynamic response and the relationship between loads and vibration fundamental frequencies of the bolt in the role of damping，in considering the impact of anchoring medium of the bolt on dynamic and static damping and based on wave theory，the wave equation，which is about the elastic vibration of the bolt when suffered by transient excitation，was established．Analytical solution of displacement field of the bolt was solved under the boundary condition that it is fixed at the one end of the bolt and it is free at the other end of the bolt．The theoretical result shows there is a second order power function relationship between the fundamental frequency and load．In order to verify the theoretical result，the pullout test and nondestructive test of the indoor model bolts were used，through the spectrum analysis of the dynamic testing signals，the fundamental frequency was obtained under the corresponding load．Fitting function relationship between load and fundamental frequency by using the least squares also presents a second order power function relationship，the load and fundamental frequency are positively correlated when the load is less than the grip between the medium and bolt-rod，but it is the negative correlation be-tween both when the load is more than the grip，and the results are consistent with the theoretical analysis．

Key words:bolt;transient dynamic response;dynamic and static damping;working condition;fundamental frequency